Построение графика функции методом дифференциального исчисления
Существует способ построения графика функции, основанный на аналитическом исследовании функции. Исследование проводится по следующей примерной схеме:1) выяснение области определения функции;
2) решается вопрос о четности или нечетности функции;
3) исследуется периодичность функции;
4) находят точки пересечения кривой с осями координат;
5) находят точки разрыва функции и определяют их характер;
6) проводят исследования на экстремум, находят экстремальные значения функции;
7) ищутся точки перегиба и интервалы выпуклости и вогнутости кривой;
8) отыскание асимптот кривой;
9) полученные результаты наносят на чертеж и получают график исследуемой функции.
Построить график без исследования функции (получить просто рисунок) можно с помощью этого сервиса.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции
Примеры
≡ x^2/(x+2)cos2(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)
Пример №1. Провести полное исследование функции и построить ее график.
Провести полное исследование функции и построить ее график.
1) Функция определена всюду, кроме точек .
2) Функция нечетная, так как f(-x) = -f(x), и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке , причем , . Попутно отметим, что прямая – вертикальная асимптота.
6) Находим и приравниваем ее к нулю: , откуда x1 = -3, x2 = 0, x3 = 3. На экстремум надо исследовать только точку x=3 (точку x2=0 не исследуем, так как она является граничной точкой промежутка [0, +∞)).
В окрестности точки x3=3 имеет: y’>0 при x<3 и y ’<0 при x>3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2.
Для проверки правильности нахождения минимального и максимального значения.
7) Находим . Видим, что y’’=0 только при x=0, при этом y”<0 при x<0 и y”>0 при x>0, следовательно, в точке (0,0) кривая имеет перегиб. Иногда направление вогнутости может измениться при переходе через разрыв кривой, поэтому следует выяснить знак y” и около точек разрыва функции. В нашем случае y”>0 на промежутке (0, ) и y”<0 на (, +∞), следовательно, на (0, ) кривая вогнута и выпукла на (, ∞).
8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты установлено выше. Ищем горизонтальные: , следовательно, горизонтальных асимптот нет.
Найдем наклонные асимптоты: , , следовательно, y=-x – наклонная двусторонняя асимптота.
9) Теперь, используя полученные данные, строим чертеж:
Пример №2.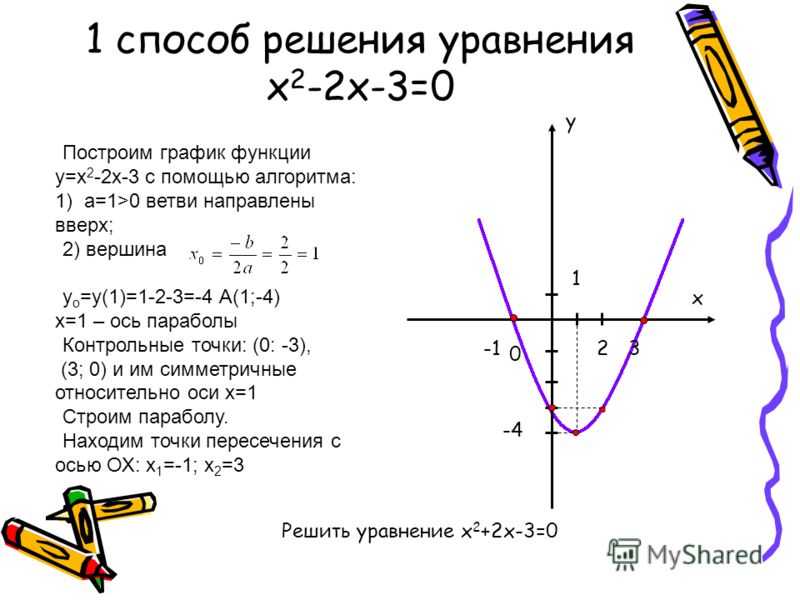 Построить график функции .
Построить график функции .
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем
; .
4. Точки разрыва x=0, причем ; следовательно, x=0 является вертикальной асимптотой графика.
Найдем наклонные асимптоты:
;
.
Наклонная асимптота имеет уравнение y=x.
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем . Существует единственная критическая точка
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Построение графиков функций онлайн
Этот сервис создан в помощь школьникам и студентам в изучении математики (алгебры и геометрии) и физики и предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (графиков по значениям), а также графиков функций в полярной системе координат.
Просто введите формулу функции в поле «Графики:» и нажмите кнопку «Построить».
Почитайте в cправкe, как правильно вводить формулы функций.
Загляните в раздел примеров, наверняка, там есть графики функций, похожие на то, что нужно Вам, останется только слегка откорректировать готовые формулы функций.
Дополнительно на нашем сайте вы можете воспользоваться калькулятором матриц, с помощью которого можно производить различные преобразования и действия с матрицами онлайн. (1/n)
(1/n)
()
| |Список функций
| Имя | Описание | |
|---|---|---|
log2(x)
|
логарифм по основанию 2 от x | |
lg(x) или log10(x)
|
логарифм по основанию 10 от x | |
log(x;b)
|
логарифм x по основанию b log(x;3) | |
ln(x)
|
натуральный логарифм (логарифм по основанию e (2. x x
|
экспонента от х (e в степени x) |
sqrt(x)
|
квадратный корень из x | |
sign(x)
| функция знака: -1 если x<0, 1 если x>0 и 0 если x=0 | |
| Тригонометрические функции | ||
sin(x)
|
синус х | |
cos(x)
|
косинус х | |
tg(x) или
tan(x)
|
тангенс х | |
ctg(x) или
cot(x)
|
котангенс х | |
arcsin(x) или
asin(x)
|
арксинус х | |
arccos(x) или
acos(x)
|
арккосинус х | |
arctg(x) или
atan(x)
|
||
arcctg(x) или
acot(x)
|
арккотангенс х | |
sinh(x) или
sh(x)
|
гиперболический синус х | |
cosh(x) или
ch(x)
|
гиперболический косинус х | |
tanh(x) или
th(x)
|
гиперболический тангенс х | |
coth(x) или
cth(x)
|
гиперболический котангенс х | |
asinh(x)
|
гиперболический арксинус х | |
acosh(x)
|
гиперболический арккосинус х | |
|
гиперболический арктангенс х | |
acoth(x)
|
гиперболический арккотангенс х | |
Встроенные константы
| Имя | Описание |
|---|---|
pi
|
Пи = 3,14. .. ..
|
e
|
e = 2,71828… число Эйлера |
Function Grapher — Калькулятор графиков
Алгебра Решатели
9x», графограф будет отображать экспоненциальную функцию.
Введите функцию: \(f(x) = \)
(Необязательно) Минимум x
(Необязательно) Максимум x
Этот калькулятор графиков позволяет вам построить график функции \(f(x)\), которую вы предоставляете, для заданного нижнего и
указанные вами верхние пределы.
Так что же на самом деле делает этот создатель диаграмм? По сути, он создаст оси координат и отобразит все пары \((x, f(x))\), для всех \(x\) в пределах указанных вами нижнего и верхнего пределов.
Какие функции я могу построить с помощью этого графического редактора?
Вы можете подумать: «Могу ли я нарисовать любую функцию, которую захочу?» Ответ да, и нет. Вы можете построить ВСЕ функции, которые можно записать в виде простого алгебраического выражения, которое хорошо определено в указанной вами области. В противном случае создатель сюжета не даст ожидаемых результатов.
Обратите внимание, что часто круглые скобки не будут иметь никакого эффекта, когда можно использовать ассоциативное свойство, но также
бывают случаи, когда при перемещении скобок все кардинально меняется.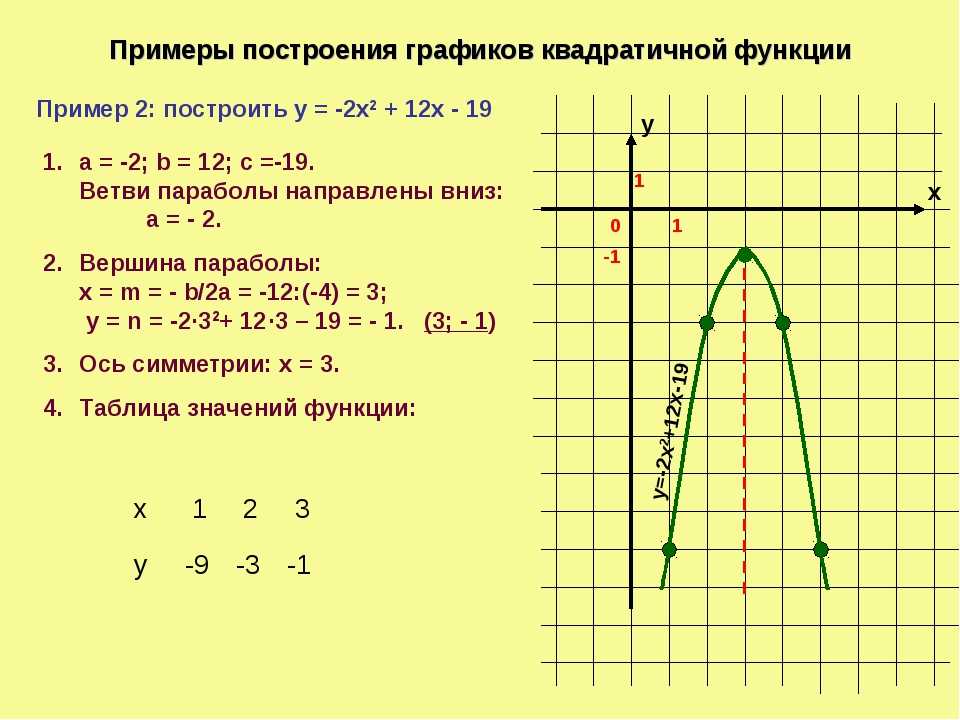
Другой специальный калькулятор графов, который может вас заинтересовать, — это создатель точечной диаграммы , используется для построения графика точек \((x_i, y_i)\) из двух выборок.
Другие графические калькуляторы
Студенты любят инструменты для построения графиков, и эта функция плоттера очень популярна. Но есть класс функций, который тригонометрические функции, требующие специального рассмотрения.
Наш калькулятор графиков триггеров не только построит для вас график, но и также даст вам связанные параметры, такие как период, частота, амплитуда и фазовый сдвиг.
Алгебра Решатель Исчисление Решатель Калькулятор диаграмм График функций онлайн Функция Плоттер Графический инструмент
Онлайн-калькулятор графиков — Рисование онлайн-кривой — Онлайн-график
Программное обеспечение для построения кривых онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функциональное исследование ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Построитель кривых особенно подходит для функциональное исследование ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
Операторы для использования в 9Для питания
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- arctan (арктангенс), арктангенс графика
- ч (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- косек (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- exp (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- -й (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
Онлайн-построитель кривых имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести касательную функции в точке для этого, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0040 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт выполняется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.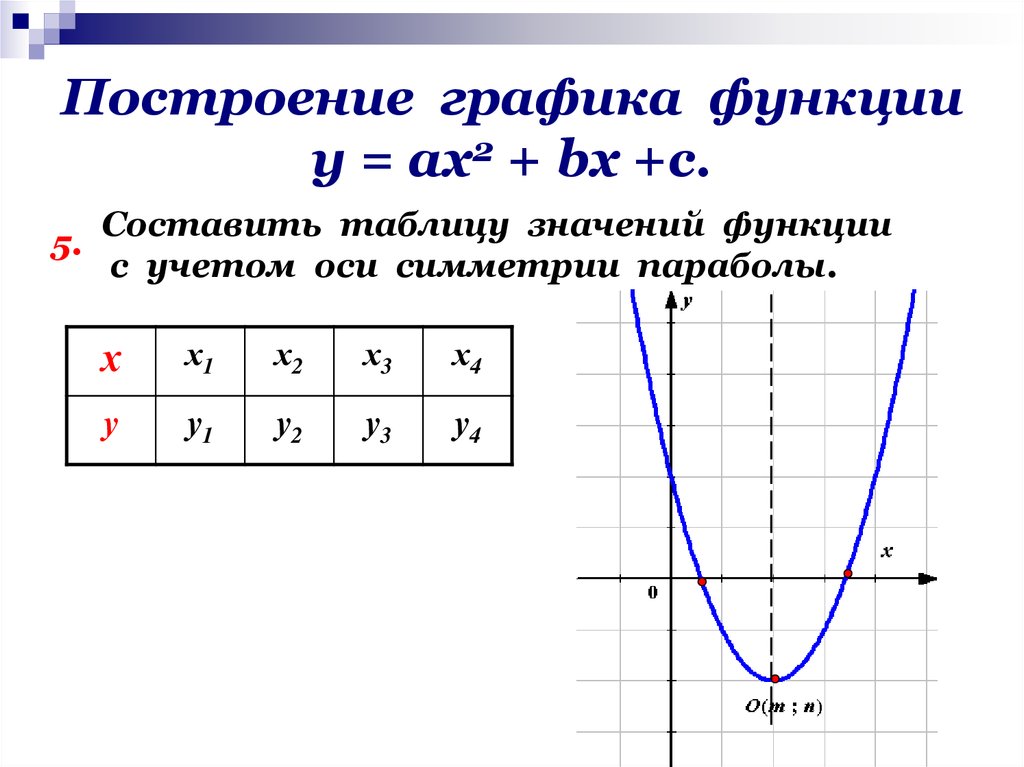
Ваш комментарий будет первым