Desmos – онлайн графический калькулятор — Версия для печати
Случалось ли вам, что нужно быстро нарисовать график функции, а под рукой нет любимой десктопной программы? Меня не раз спасал бесплатный онлайн графический калькулятор от компании Desmos [1]. Мультиязычный интерфейс, в т.ч. с поддержкой русского языка.
Desmos — это онлайн-сервис, который позволяет создавать графики по формуле функции. Сама функция вписывается в левый столбец, а график автоматически строится в правой части. Сервис будет полезен тем, кому необходимо быстро и просто построить график функции, для кого построение графиков функций вызывает сложности или тем, кому с наименьшими затратами необходимо проверить правильность построения графика.
Кроме того, что Desmos Calculator может выполнять все функции обычных графических калькуляторов, он также имеет несколько дополнительных возможностей, которых нет у обычных графических калькуляторов.
Что можно делать в DC:
- рисовать функциями;
- создавать анимированные картинки с помощью привязки объектов к функциям с параметрами;
- создавать динамическую наглядность;
- быстро создавать скриншоты с формулами и функциями.

Desmos Calculator может строить следующие графики:
- Постоянная функция
- Зависимость x от y
- Неравенства
- Графики в полярной системе координат
- Кусочно-заданные функции
- Точка
- Группа точек
- Подвижная точка
- Функции с параметром
- Сложные функции
При построении графиков можно использовать следующие функции:
- Степенные, показательные и логарифмические функции
- Тригонометрические функции
- Обратные тригонометрические функции
- Гиперболические функции
- Статистические функции и функции вероятностей
- Другие функции
В библиотеке готовых приложений можно найти немало динамических апплетов для функций разного типа (от линейной до тригонометрической) со встроенными «ползунками».
Авторизация в сервисе позволяет сохранять созданные апплеты и делиться ими в виде ссылки, встроенного кода или картинки.
Подробную информацию по построению графиков функций вы найдете в источниках, опубликованных в подвале статьи.
Руководство по быстрой публикации графика функции, созданного в Desmos:- Перейти по ссылке https://www.desmos.com/calculator [1]
- Зарегистрируйтесь или войдите в свой аккаунт (правый верхний угол)
- Постройте график нужной функции
- Сохраните график
- Опубликуйте ссылку на свой график или сохраните в виде картинки
Источники:
- Desmos. Руководство пользователя (рус., PDF)
- Desmos. Обучающие материалы (англ.) [3]
- Desmos. Канал с обучающими роликами на YouTube (англ.) [4]
- DESMOS – замечательный инструмент для учителей математики (рус.) [5]
- Применение Desmos на уроках математики в школе (рус.) [6]
Автор: kbotalov
Источник [7]
[1] графический калькулятор от компании Desmos: https://www. desmos.com/calculator
desmos.com/calculator
[2] Desmos. Руководство пользователя (рус., PDF): https://desmos.s3.amazonaws.com/Desmos_User_Guide_RU.pdf
[3] Desmos. Обучающие материалы (англ.): http://learn.desmos.com/
[4] Desmos. Канал с обучающими роликами на YouTube (англ.): https://www.youtube.com/playlist?list=PLfM6zMGnbgOGLZc-_Yj3QVK3Vz_L4Cw59
[5] DESMOS – замечательный инструмент для учителей математики (рус.): http://didaktor.ru/desmos-zamechatelnyj-instrument-dlya-uchitelej-matematiki/
[6] Применение Desmos на уроках математики в школе (рус.): https://edugalaxy.intel.ru/index.php?automodule=minerva&CODE=showTaglist&tag=Desmos
Построение графика при помощи утилиты gnuplot
Gnuplot — свободная и кроссплатформенная утилита
для визуализации научных (и не только) данных
Gnuplot — это свободный инструмент для создания графиков. Поддерживается создание как двухмерных, так и трехмерных изображений.
Программа доступна для множества платформ — Linux, MS Windows, OSX и представляет собой утилиту командной строки, с собственным набором команд. Так же имеется возможность выполнять скрипты. Поддерживается вывод как непосредственно на экран, так и в файлы различных графических форматов.
Утилита очень удобна для визуализации и глубокого анализа различных научных данных. Встроенный скриптовый язык позволяет гибко задавать различные параметры визуализации.
Официальный сайт проекта — http://www.gnuplot.info/
Распространяется как в виде исходных кодов, так и в виде уже собранных пакетов и установочных файлов для различных операционных систем. В случае большинства дистрибутивов Linux программа доступна в репозиториях и устанавливается штатными средствами дистрибутива. Для Apple OSX установка доступна, например, через macports (см. http://www.macports.org/)
В сети и в частности на официальном сайте доступны множество примеров использования gnuplot, русскоязычной же информации увы крайне мало.
В этой статье я рассмотрю несколько типовых примеров использования gnuplot в формате «подставил свои данные — получил график».
Для начала рассмотрим основные команды, которые будут актуальны практически каждый раз. Важный момент — все команды регистрозависимые, так что команда help будет понята утилитой, а вот Help — уже нет.
help — собственно помощь, богатая встроенная интерактивная справка, можно получать справку по конкретной команде, например help plot
set xlabel «моя подпись для x» — задает подпись для оси абсцисс
set ylabel «моя подпись для y» — задает подпись для оси ординат
set xrange [min:max] — задает лимиты значений для оси абсцисс, после выполнения команды ось на графике будет размечена от min до max, значения графика не попавшие в этот диапазон будут отброшены. Этот параметр может быть полезен для фильтрации ненужных значений или же для визуального отодвигания начала и конца графика от краев изображения.

Если вместо конкретного значения указать * — значение будет вычисляться автоматически, на основе минимального/максимального значения в данных.
По умолчанию gnuplot использует режим [*:*] с автоматическим вычислением.
set yrange [min:max] — аналогично xrange, только для оси ординат.
plot — собственно команда построения графика, эта команда принимает обязательный аргумент — источник данных для построения графика, это может быть имя файла с исходными данными, либо же математическая формула.
Есть возможность, через запятую, задать несколько источников данных — тогда на одном «полотне» будут нарисованы несколько графиков, так же можно указывать дополнительные параметры — тип графика, параметры отрисовки. Об этом в примерах ниже.
set terminal <term_type> — служебная команда, задает механизм вывода графика, по умолчанию вывод выполняется на экран (если доступна графическая оболочка), для переключения в режим записи в png файл следует выполнить команду set terminal png для возвращения в режим отображения на экране следует выполнить эту команду с иным аргументом:
Для Windows: set terminal windows
Для Linux: set terminal X11
Для OSX: set terminal aqua
Полный список доступных терминалов можно узнать, если просто выполнить команду set terminal
set output «filename.
 png» — задает имя выходоного файла, в случае если выбран соответствующий режим в set terminal
png» — задает имя выходоного файла, в случае если выбран соответствующий режим в set terminalset key <param>
set nokey — выключить отображение легенды
set key — включить ранее выключенное отображение легенды
set key title «подпись» — задает произвольную подпись к легенде
set key {left | right | center} {top | bottom | center} — комбинацией параметров можно задать расположение легенды
reset — сброс всех заданных параметров
Теперь настало время примеров, построим простейший график функции sin(x), установив легенду с произвольным текстом и расположением. Так же зададим ограничения значений по X
Запускаем gnuplot и вводим следующие команды (где > — приглашение командной строки gnuplot)
> set xrange [-2:5]
> set key horizontal top left
> set key title «график функции sin(x)»
> plot sin(x)
После выполнения последней команды откроется окно с нарисованным графиком
Теперь рассмотрим более реальный пример — например зависимость уровня радиации от высоты.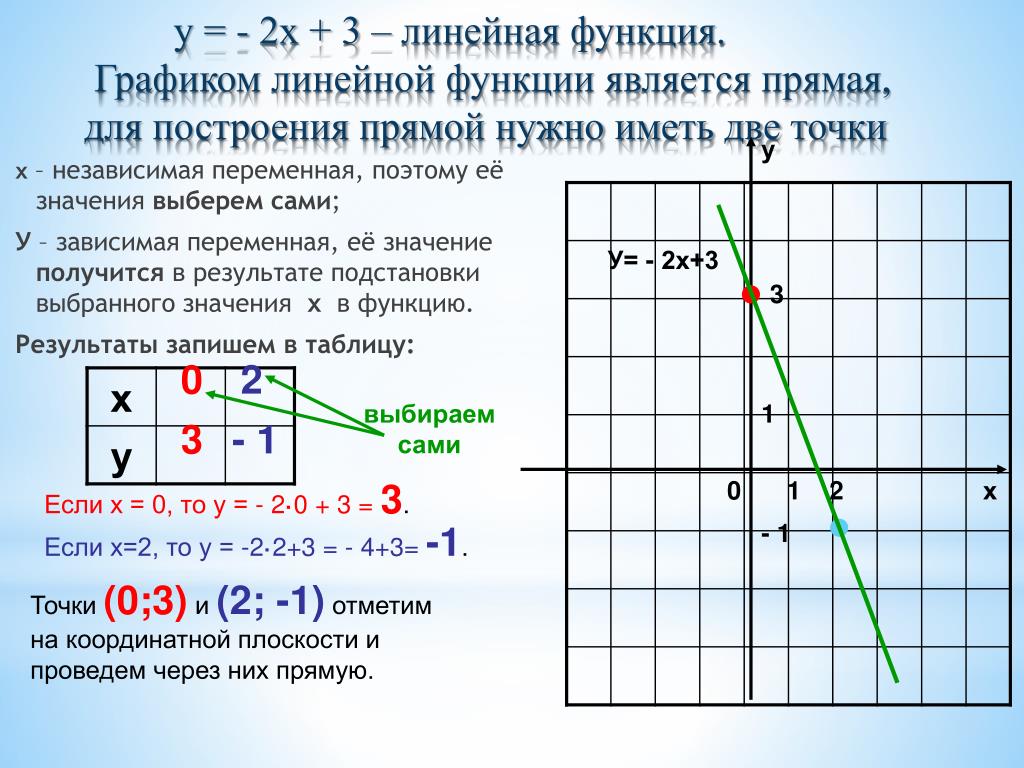
У нас есть исходные данные — высота в метрах и уровень радиации в микрозивертах.
Сохраним эти данные в текстовый файл, в виде двух колонок (обязательное условие — разделителем дробной части должны быть точки)
220 0.1
500 0.1
1000 0.1
1500 0.1
2000 0.1
2500 0.11
3000 0.12
3500 0.13
4000 0.14
4500 0.18
5000 0.2
5500 0.22
6000 0.25
6500 0.29
Где в первой колонке — высота, это будут значения для X, а во второй колонке — микрозиверты, значения для Y.
Сохраним эти данные в некий тектовый файл radiation.txt
Теперь в текущем каталоге (где сохранен файл с данными) запускаем gnuplot и вводим следующие команды:
> set xrange [100:7000]
> set ylabel «Уровень радиации»
> set xlabel «Высота»
> plot «radiation.txt» with lines
В итоге на экране мы получим график
В последней команде мы «попросили» gnuplot построить график по данным из файла radiation. txt, так же было дополнительно указана опция with lines что означает использовать сплошную кривую для отрисовки графика.
txt, так же было дополнительно указана опция with lines что означает использовать сплошную кривую для отрисовки графика.
Еще возможные варианты команды позволяют нарисовать графики вида:
> plot «radiation.txt» with points
> plot «radiation.txt» with boxes
Для варианта with points можно так же задать дополнительные параметры — тип точек, делается это с помощью дополнительного аргумента pointtype <num>, где num — некое целое число, означающее тип точки. Попробуйте самостоятельно поиграть с этим значением и посмотреть какой тип точки будет нарисован, вот некоторые примеры:
> plot «radiation.txt» with points pointtype 5
> plot «radiation.txt» with points pointtype 6
Рассмотрим другую распространенную ситуацию — есть несколько наборов данных и необходимо нарисовать несколько графиков сразу, для удобного визуального сравнения.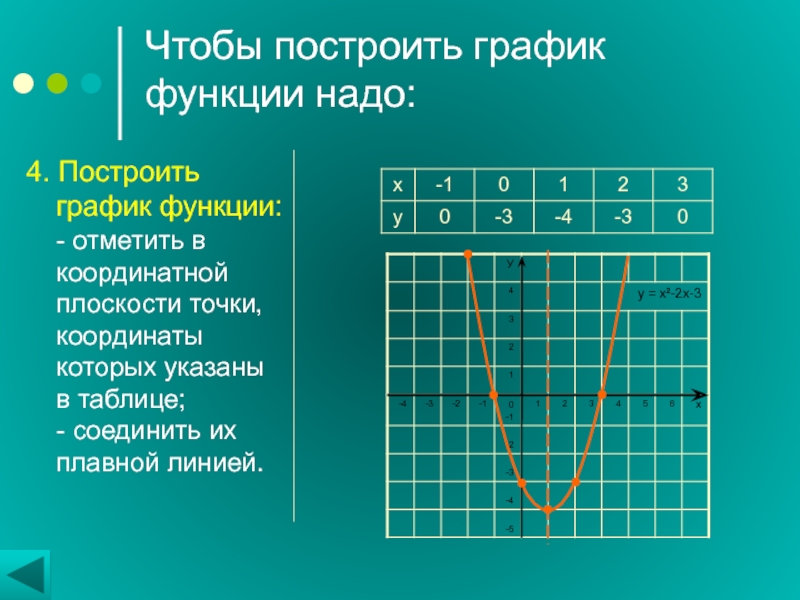
Сделать это очень просто. Подготовим еще один набор данных и сохраним его в файл radiation2.txt
120 0.1
500 0.11
1000 0.12
1500 0.12
2000 0.12
2500 0.13
3000 0.14
3500 0.16
4000 0.17
4500 0.19
5000 0.21
5500 0.25
6000 0.32
6500 0.46
Запускаем gnuplot и выполняем уже знакомую последовательность команд:
> set xrange [100:7000]
> set ylabel «Уровень радиации»
> set xlabel «Высота»
А теперь просим программу построить сразу два графика, еще и задав произвольные заголовки для легенд, делается это сразу одной строчкой
> plot «radiation.txt» with lines title «Радиация 1», «radiation2.txt» with lines title «Радиация 2»
В итоге получим график
Очень просто. Количество наборов данных может быть произвольным — просто указываются через запятую, как в данном случае.
Теперь построим точно такой же график, но вместо вывода на экран сразу сохраним в png файл:
> set xrange [100:7000]
> set ylabel «Уровень радиации»
> set xlabel «Высота»
> set terminal png
> set output «plot. png»
png»
> plot «radiation.txt» with lines title «Радиация 1», «radiation2.txt» with lines title «Радиация 2»
После выполнения команды в текущем каталоге появится файл plot.png с изображением графика. Как видно данная операция отличается вводом двух дополнительных команд, описанных в начале настоящей статьи.
А теперь для примера рассмотрим принципы построения трехмерных графиков.
Для построения объемного графика нам нужна третья координата — Z, подготовим текстовый файл 3d.txt с таким набором данных
9.862e-01 -8.062e-02 0.001
9.786e-01 -1.134e-01 0.002
9.720e-01 -1.382e-01 0.003
-1.849e-01 -2.165e-01 80.000
-2.412e-01 -1.301e-01 90.000
-2.611e-01 -4.825e-02 100.000
Далее выполняем команды gnuplot:
> set xrange [-1:1]
> set yrange [-1:1]
> splot «3d.txt» with lines
Внимательный читатель сразу заметит, что вместо plot мы используем команду splot, именно она позволяет создать трехмерный график, корректно обрабатывая данные.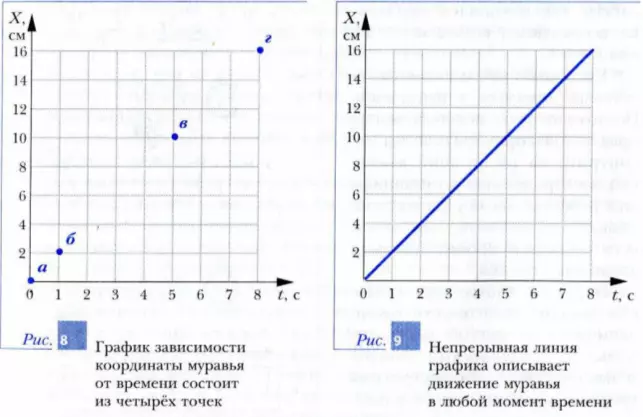 Если же использовать старую команду plot — будет построена некая двухмерная проекция предполагаемого графика.
Если же использовать старую команду plot — будет построена некая двухмерная проекция предполагаемого графика.
После выполнения команды мы получим вот такое симпатичное изображение:
Исходных данных у нас не очень много, поэтому изображение выглядит не так впечатляюще, как могло бы выглядеть, но тем не менее мы можем попробовать отобразить эти данные в виде трехмерной поверхности, для этого добавим новую команду:
> set dgrid3d 30,30
Команда создает трехмерную сетку размером 30 на 30, наши же данные будут вытянутыми вершинами в этой сетке, генерация графика осуществляется как и в примере выше, в итоге получаем изображение:
Познакомиться более глубоко с принципами построения трехмерных графиков можно тут: http://gnuplot.sourceforge.net/demo/surface1.html
Приведено достаточно много примеров на все случаи жизни.
Еще больше захватывающих примеров: http://gnuplot.sourceforge.net/demo/
Более подробную информацию можно почерпнуть в официальной документации.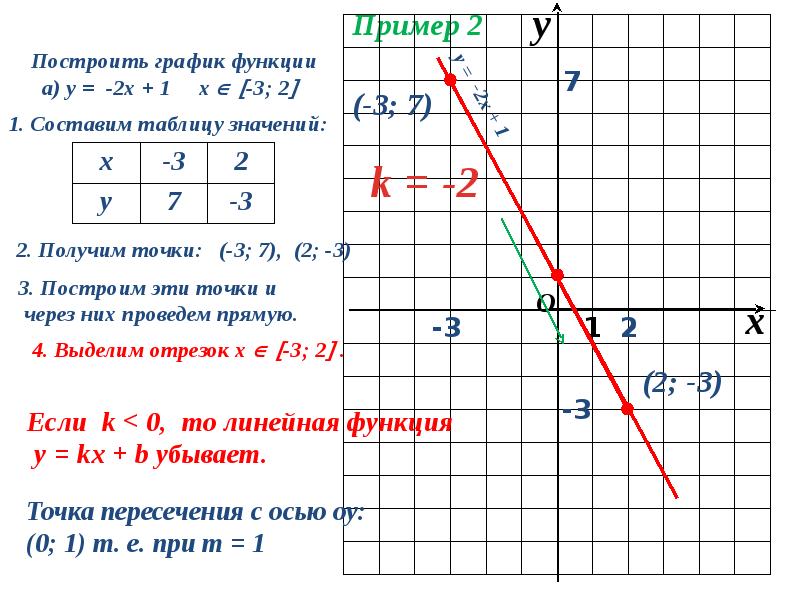 Так же не забывайте про команду help.
Так же не забывайте про команду help.
Успехов!
P.S. Построение графиков может пригодиться Вам при астрометрии и фотометрии звезд (или астероидов, комет, спутников…) и конечно при поиске новых переменных звезд.
Кутков О.Е., КрАО
2015г
Рекомендуем:
Астробиблиотека
Астроканикулы
Диаграмма рассеяния в R | Блог SixSigmaOnline.ru
Диаграмма scatterplot (или диаграмма рассеяния) помогает визуализировать взаимосвязь между двумя непрерывными переменными. Наряду с другими программами для анализа данных и графики, в статистическом пакете R реализовано множество вариантов представления данного типа диаграмм как в базовой версии, так и с помощью дополнительно устанавливаемых пакетов. Рассмотрим возможности R для построения таких графиков на примере фактических данных из сферы сельского хозяйства. Данные анализировались автором статьи в своей практической деятельности для оценки силы зависимости выращенного урожая пшеницы от количества использованных минеральных удобрений за несколько лет наблюдений.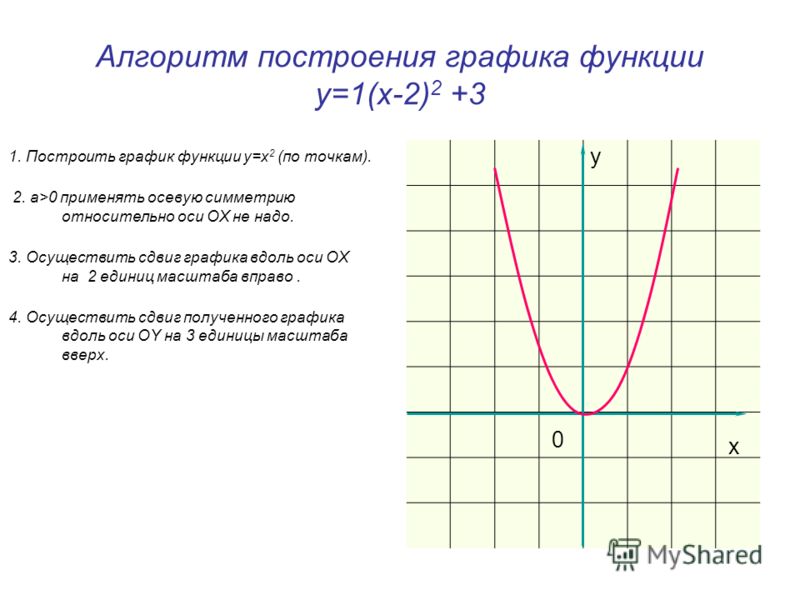
В базовой версии программы R для построения scatterplot используется функция plot(x,y), где x и y – числовые вектора (переменные значения), определяющие координаты точек на диаграмме. Таблица с данными была предварительно сформирована в программе Excel и далее загружена в среду R с помощью пакета library(readxl). Вот так выглядит фрагмент таблицы:
В нашем случае x= количество удобрений, y=объем урожая.
Значения переменных измеряются в тоннах, а каждое отдельное наблюдение за каждый год – это поле со своей площадью и с примерно равным объемом внесения удобрений на единицу этой площади (гектар).
Таким образом, используя базовую функцию plot, получаем следующий график, показывающий практически идеальную линейную зависимость объема выращенного урожая от количества применяемых удобрений.
Программный код выглядит следующим образом:
> plot(удобрения, урожай, data=g, col=»red», xlab=»К-во удобрений, т», ylab=»Объем урожая пшеницы, т») |
Команда data в программном коде определяет таблицу данных или объект, который содержит необходимые для построения графика переменные в поименованных колонках или векторах.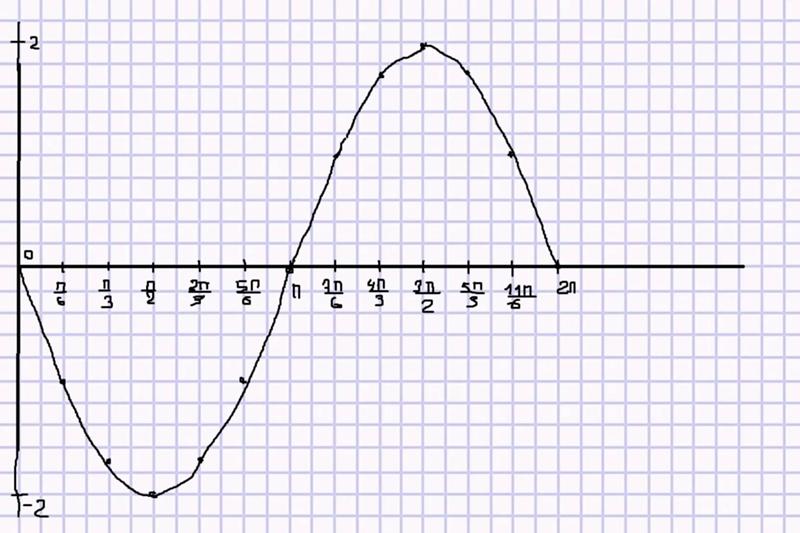 Другие команды, указанные в скобках кода, задают атрибуты оформления самого графика (цвет точек на диаграмме, подписи осей и т.д).
Другие команды, указанные в скобках кода, задают атрибуты оформления самого графика (цвет точек на диаграмме, подписи осей и т.д).
При необходимости можно добавить на график аппроксимирующую регрессионную линию с помощью функции abline() или сглаживающую кривую функцией lowess(). Программный код ниже:
> abline(lm(урожай~удобрения, data=g), col=»blue», lwd=1, lty=1) |
В данном случае аппроксимирующая и сглаживающая линии практически совпадают, так как видимый разброс данных имеет прямой линейный характер.
Команда lm(formula или “~”) – основная функция в R для подгонки регрессионных моделей. Формула означает, что значение y (урожай) мы будем предсказывать по значению x (удобрения). Записывается формула через знак “~”. Обратите внимание, что в графической функции plot() сначала записывается переменная x и далее через запятую y – как координаты осей для построения графика.
Дополнительные пакеты R значительно расширяют стандартные возможности программы.
Например, установив пакет library(car), мы можем построить график для данных, разбитых на подгруппы или факторы. В нашем случае мы определяем разницу во взаимосвязи 2 переменных на 2 уровнях фактора «год»: 2017 и 2018.
> library(car) |
Функция scatterplot из пакета car позволяет нам увидеть различия в данных по годам.
Как видно в программном коде, уровень фактора задается через вертикальную черту справа от записи формулы.
Также удобно рассматривать данные в виде матрицы – особенно если мы работаем не с одной парой переменных, а с несколькими. В базовом варианте функция pairs() используется для этой цели.
Формат записи на примере встроенной в R таблицы данных Duncan:
> pairs(~income+education+prestige, data=Duncan, col=»red», pch=15) |
Все переменные, указанные справа от знака “~”, показываются на графике.
Здесь мы имеем 3 переменные с графиком взаимосвязи для каждой пары. Матрица содержит 6 графиков: 3 в верхней панели и 3 в нижней панели от диагонали с названиями переменных. Они идентичны.
Верхнюю или нижнюю панель можно отключить, добавив в код соответствующую команду:
> pairs(~income+education+prestige, data=Duncan, col=»red», pch=15, upper.panel=NULL) |
Подобную матрицу, но с дополнительными опциями, можно построить с помощью уже упомянутого пакета car:
> scatterplotMatrix(~урожай+удобрения|год, data=g, col=3:4, pch=c(15,16), cex=1.0, var.labels=c(«Валовый урожай, т», «Удобрение, т»)) |
Здесь функция scatterplotMatrix по умолчанию дает нам возможность к основным графикам рассеивания построить графики плотности распределения, а также, например, выделить зоны на графике с высокой концентрацией наблюдений в виде эллипсов.
> scatterplotMatrix(~урожай+удобрения|год, data=g, col=3:4, pch=c(15,16), cex=1.0, var.labels=c(«Валовый урожай, т», «Удобрение, т», ellipse=TRUE)) |
Согласитесь, что данные типы диаграмм достаточно хорошо и информативно дополнят любой рабочий отчет или проект 6σ.
Естественно, что возможности среды R описанными выше функциями не ограничиваются. Но в любом случае, чтобы больше узнать, какие значения возвращает любая функция в рабочем окне программы, можно набрать для примера: “help(scatterplot)” или “?scatterplot”.
Python построение графиков в реальном времени
Я получаю некоторые данные в двух массивах: один для времени и один для значения. Когда я достигаю 1000 точек, я запускаю сигнал и plot этих точек (x=время, y=значение).
Мне нужно сохранить на том же рисунке предыдущие сюжеты, но только разумное количество, чтобы не замедлять процесс.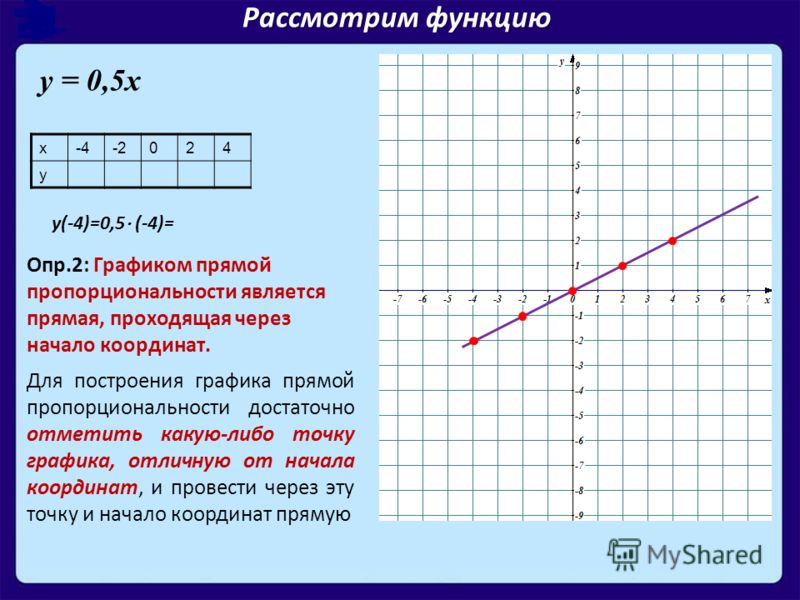 Например, я хотел бы сохранить 10 000 точек на своем графике.
matplotlib interactive plot работает нормально, но я не знаю, как стереть первые точки, и это очень быстро замедляет работу моего компьютера.
Я заглянул в matplotlib.animation, но это только кажется повторением того же самого plot, а на самом деле не актуализирует его.
Например, я хотел бы сохранить 10 000 точек на своем графике.
matplotlib interactive plot работает нормально, но я не знаю, как стереть первые точки, и это очень быстро замедляет работу моего компьютера.
Я заглянул в matplotlib.animation, но это только кажется повторением того же самого plot, а на самом деле не актуализирует его.
Я действительно ищу легкое решение, чтобы избежать любого замедления.
Поскольку я получаю очень большое количество времени, я стираю входные данные на каждом цикле (1001-я точка хранится в 1-й строке и так далее).
Вот что у меня есть на данный момент, но он сохраняет все точки На графике:
import matplotlib.pyplot as plt
def init_plot():
plt.ion()
plt.figure()
plt.title("Test d\'acqusition", fontsize=20)
plt.xlabel("Temps(s)", fontsize=20)
plt.ylabel("Tension (V)", fontsize=20)
plt.grid(True)
def continuous_plot(x, fx, x2, fx2):
plt.plot(x, fx, 'bo', markersize=1)
plt.plot(x2, fx2, 'ro', markersize=1)
plt. draw()
draw()
Я вызываю функцию init один раз, и continous_plot находится в процессе, вызываемом каждый раз, когда у меня есть 1000 точек в моем массиве.
python plot real-timeПоделиться Источник CoMartel 16 июля 2014 в 14:32
4 ответа
- Хорошая основа для живого построения графиков в Python?
Я работаю над приложением Python, которое включает в себя регрессионный анализ живых данных и построение графиков. То есть приложение получает данные в реальном времени, а регрессионные модели пересчитываются по мере обновления данных. Обратите внимание, что я хочу построить как входные данные…
- Java построение графиков в реальном времени
Я ищу способ построить инкрементный график в реальном времени, имея огромную базу данных на бэкэнде. Там будут миллионы транзакций, которые будут храниться, и график должен отражать изменения в базе данных на регулярной основе; скажем, каждый через секунду.
 Есть какие-нибудь предложения по Java…
Есть какие-нибудь предложения по Java…
7
Самое легкое решение, которое у вас может быть, — это заменить значения X и Y существующего plot. (Или только значение Y, если ваши данные X не изменяются. Простой пример:
import matplotlib.pyplot as plt
import numpy as np
import time
fig = plt.figure()
ax = fig.add_subplot(111)
# some X and Y data
x = np.arange(10000)
y = np.random.randn(10000)
li, = ax.plot(x, y)
# draw and show it
ax.relim()
ax.autoscale_view(True,True,True)
fig.canvas.draw()
plt.show(block=False)
# loop to update the data
while True:
try:
y[:-10] = y[10:]
y[-10:] = np.random.randn(10)
# set the new data
li.set_ydata(y)
fig.canvas.draw()
time.sleep(0.01)
except KeyboardInterrupt:
break
Это решение также довольно быстрое. Максимальная скорость приведенного выше кода составляет 100 перерисовок в секунду (ограничена time. ), я получаю около 70-80, что означает, что одна перерисовка занимает около 4 мс. Но YMMV в зависимости от бэкенда и т. д. sleep
sleep
Поделиться DrV 16 июля 2014 в 17:34
5
Используйте массив фиксированного размера и plot, который использует matplot.
import collections
array = collections.deque([None] * 1000, maxlen=1000)
Когда вы добавите его в массив, он удалит первый элемент.
Поделиться f.rodrigues 16 июля 2014 в 18:07
0
Я знаю, что опоздал ответить на этот вопрос, но для вашей проблемы вы могли бы заглянуть в пакет «joystick». Он основан на методах line.set_data() и canvas.draw() с дополнительным масштабированием осей. Он также позволяет осуществлять интерактивное ведение журнала текста или построение изображений (в дополнение к построению графиков). Нет необходимости делать свои собственные циклы в отдельном потоке, пакет заботится об этом, просто дайте частоту обновления, которую вы хотите. Кроме того, консоль остается доступной для дополнительных команд мониторинга.
Увидеть http://www.github.com/ceyzeriat/джойстик/ или https://pypi.python.org/pypi/джойстик (использовать pip установить джойстик, чтобы установить)
Нет необходимости делать свои собственные циклы в отдельном потоке, пакет заботится об этом, просто дайте частоту обновления, которую вы хотите. Кроме того, консоль остается доступной для дополнительных команд мониторинга.
Увидеть http://www.github.com/ceyzeriat/джойстик/ или https://pypi.python.org/pypi/джойстик (использовать pip установить джойстик, чтобы установить)
пробовать:
import joystick as jk
import numpy as np
import time
class test(jk.Joystick):
# initialize the infinite loop decorator
_infinite_loop = jk.deco_infinite_loop()
def _init(self, *args, **kwargs):
"""
Function called at initialization, see the doc
"""
self._t0 = time.time() # initialize time
self.xdata = np.array([self._t0]) # time x-axis
self.ydata = np.array([0.0]) # fake data y-axis
# create a graph frame
self.mygraph = self.add_frame(jk.Graph(name="test", size=(500, 500), pos=(50, 50), fmt="go-", xnpts=10000, xnptsmax=10000, xylim=(None, None, 0, 1)))
@_infinite_loop(wait_time=0. 2)
def _generate_data(self): # function looped every 0.2 second to read or produce data
"""
Loop starting with the simulation start, getting data and
pushing it to the graph every 0.2 seconds
"""
# concatenate data on the time x-axis
self.xdata = jk.core.add_datapoint(self.xdata, time.time(), xnptsmax=self.mygraph.xnptsmax)
# concatenate data on the fake data y-axis
self.ydata = jk.core.add_datapoint(self.ydata, np.random.random(), xnptsmax=self.mygraph.xnptsmax)
self.mygraph.set_xydata(t, self.ydata)
t = test()
t.start()
t.stop()
2)
def _generate_data(self): # function looped every 0.2 second to read or produce data
"""
Loop starting with the simulation start, getting data and
pushing it to the graph every 0.2 seconds
"""
# concatenate data on the time x-axis
self.xdata = jk.core.add_datapoint(self.xdata, time.time(), xnptsmax=self.mygraph.xnptsmax)
# concatenate data on the fake data y-axis
self.ydata = jk.core.add_datapoint(self.ydata, np.random.random(), xnptsmax=self.mygraph.xnptsmax)
self.mygraph.set_xydata(t, self.ydata)
t = test()
t.start()
t.stop()
Поделиться Guillaume S 28 сентября 2016 в 22:29
- Обеспечивает ли Vaadin построение графиков в реальном времени?
Я хочу подключить несколько графиков в реальном времени в моем приложении Vaadin. Я просмотрел сэмплер Vaadin и аддоны и не смог найти ни одного. Существуют ли какие-либо доступные аддоны, которые могут обеспечить построение графиков в реальном времени (что-то вроде непрерывного линейного графика,.
 ..
.. - Динамическое построение графиков в реальном времени
У меня есть вопрос, касающийся обновления динамически разбросанных графиков с matplotlib. У меня есть следующий класс в Python »’ PolygonHandler.py — Python source for polygon handling »’ import numpy as np import matplotlib.pyplot as plt class PolygonHandler: # Constructor def __init__(self):…
0
Чтобы быть полностью интерактивным, вы можете использовать для этого Боке. Конкретно вы можете использовать функцию обновления, которая вызывается каждые X МС, и передавать новые данные потоком.
Здесь есть фрагмент, который я использую:
def update():
candle_data.stream(new_data, 300)
plot = figure(x_axis_type='datetime',x_range=(start_day, final_day), width=1500, height=900, title='Live Chart', sizing_mode='scale_both')
plot.segment(x0='time', y0='highest', x1='time', y1='lowest', color='black', source=candle_data)
plot. vbar(x='time', width = 0.5*60*60*50 ,bottom='open', top='close',fill_color='color', line_color='black', source = candle_data)
doc.add_root(column([plot]))
doc.add_periodic_callback(update, 20000)
doc.title = "Candle Data Live Rates"
vbar(x='time', width = 0.5*60*60*50 ,bottom='open', top='close',fill_color='color', line_color='black', source = candle_data)
doc.add_root(column([plot]))
doc.add_periodic_callback(update, 20000)
doc.title = "Candle Data Live Rates"
Поделиться Javier Guzman 24 июля 2018 в 07:38
Похожие вопросы:
Построение графиков научных данных в .net
Есть ли у кого-нибудь рекомендации по построению научных данных в .net (c# winforms). Некоторые из моих требований: построение графиков в реальном времени, 3D (водопад), множественная ось,…
построение графиков в режиме реального времени в Torch
Я новичок в Факеле. Я тренирую модель нейронной сети, где я хочу сделать график для обучения и ошибки проверки с каждой итерацией, быстрый поиск показывает, что я строю график с gnuplot,…
gnuplot 2-D построение графиков из массивов-в реальном времени
Я должен сделать график сканирования значений датчика в реальном времени.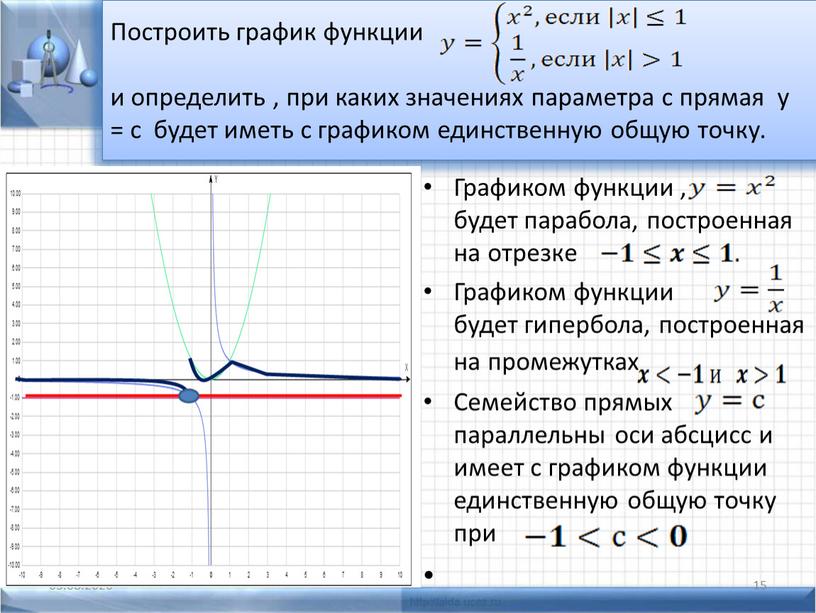 Для этой цели я использую gnuplot. До сих пор я могу общаться с gnuplot из моей программы c++. Я попробовал несколько…
Для этой цели я использую gnuplot. До сих пор я могу общаться с gnuplot из моей программы c++. Я попробовал несколько…
Хорошая основа для живого построения графиков в Python?
Я работаю над приложением Python, которое включает в себя регрессионный анализ живых данных и построение графиков. То есть приложение получает данные в реальном времени, а регрессионные модели…
Java построение графиков в реальном времени
Я ищу способ построить инкрементный график в реальном времени, имея огромную базу данных на бэкэнде. Там будут миллионы транзакций, которые будут храниться, и график должен отражать изменения в базе…
Обеспечивает ли Vaadin построение графиков в реальном времени?
Я хочу подключить несколько графиков в реальном времени в моем приложении Vaadin. Я просмотрел сэмплер Vaadin и аддоны и не смог найти ни одного. Существуют ли какие-либо доступные аддоны, которые…
Динамическое построение графиков в реальном времени
У меня есть вопрос, касающийся обновления динамически разбросанных графиков с matplotlib.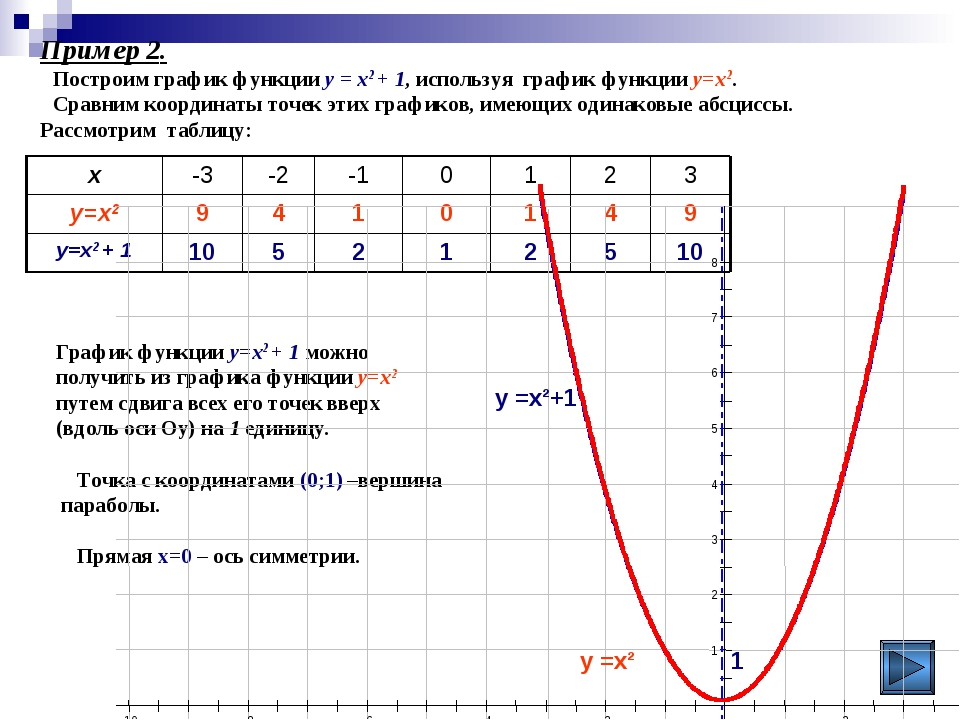 У меня есть следующий класс в Python »’ PolygonHandler.py — Python source for polygon handling »’ import…
У меня есть следующий класс в Python »’ PolygonHandler.py — Python source for polygon handling »’ import…
Android Построение Графиков В Реальном Времени
Я создаю приложение для построения акселерометра android в реальном времени с использованием achartengine. Я провел много исследований, чтобы решить проблемы, о которых упоминаю ниже, но не смог…
Python построение графиков данных в реальном времени
Я ищу способ построить линейный график данных в реальном времени или точечные графики из python. С помощью графиков я хочу отслеживать длительные циклы при экспериментировании с алгоритмами с…
Python HTML построение графика в реальном времени
Я пытаюсь включить некоторые визуализации данных в реальном времени в веб-приложение, над которым работаю В настоящее время я использую matplotlib и plotly. Проблема с matplot заключается в том, что…
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов.
| ||||
Подбор полинома по заданным точкам
| По заданным точкам построен полином |
Задача, которую решает этот калькулятор, звучит так: Построить по N -известным значениям полином N-1 степени.
Это является одним из видов аппроксимации, но практически, редко используется. Связанно это с тем, что несмотря на то что в узловых точках (исходных) значение вычсленного полинома совпадает на 100%, в промежуточных точках значение может быть очень далеким от реальных значений.
Простой пример это показывает. Пусть какому то ученому пришла в голову рассчитать аппроксимирующий полином, который показывал бы как растет человек год от года.
Он запросил данные и получил, что в первый год рост человека 50см, на 3 год — 80 см, в 6 лет -120см, в 15 лет -150 см, а в 25 лет — 180 см
Введя данные он получил следующий полином
| По заданным точкам построен полином |
Вроде бы все хорошо, в каждой контрольной точке, значения совпадают, но если мы посмотрим график. ..
..
Удивительно, но где то в 20 лет у человека рост резко уменьшается до 130 см.
Мы то с Вами прекрасно понимаем, что это не так, но в других расчетах, такая аппроксимация может приводить вот к таким «аномалиям» и следовательно к неверным выводам.
Для чего же тогда нужен этот калькулятор?
Если мы знаем(!) что наша неизвестная функция есть многочлен какой то степени, то взяв необходимое количество точек, мы всегда с высокой точностью определим эти коэффициенты.
Несколько примеров:
Я хочу определить какой многочлен поможет найти зависимость, от следующих значений, если при
1 результат
- Подстановка многочлена в другой многочлен >>
Создание графика частичной зависимости (PDP) и индивидуального условного ожидания (ICE) графики
Частичная зависимость [1] представляет отношения между
переменные-предикторы и предсказанные ответы в обученной регрессионной модели.
plotPartialDependence вычисляет частичную зависимость предсказанных ответов
на подмножестве переменных-предикторов путем маргинализации по сравнению с другими переменными.
Рассмотрим частичную зависимость от подмножества X S всего набора переменных-предикторов X = { x 1 , x 2 ,…, x м }.Подмножество X S включает либо одна переменная или две переменные: X S = { x S1 } или X S = { х С1 , x S2 }. Пусть X C будет дополнительным набор X S в X . Предсказанный ответ f ( X ) зависит от всех переменных в X :
Частичная зависимость предсказанных ответов от X S определяется ожиданием прогнозируемые ответы относительно X C :
где п. C ( X C )
— предельная вероятность X C , то есть pC (XC) ≈∫p (XS, XC) dXS.Предполагая, что каждое наблюдение равновероятно, а зависимость
между X S и X C и взаимодействие X S и X C в отзывах не сильно,
C ( X C )
— предельная вероятность X C , то есть pC (XC) ≈∫p (XS, XC) dXS.Предполагая, что каждое наблюдение равновероятно, а зависимость
между X S и X C и взаимодействие X S и X C в отзывах не сильно, plotPartialDependence оценивает частичную зависимость, используя наблюдаемые
следующие данные предиктора:
| fS (XS) ≈1N∑i = 1Nf (XS, XiC), | (1) |
, где N — количество наблюдений, а X i = ( X i S , X i C ) — это и -е наблюдение.
Когда вы вызываете функцию plotPartialDependence , вы можете указать обученный
модель ( f (·) ) и выберите переменные
( X S ) с использованием входных аргументов Mdl и Vars соответственно.
plotPartialDependence вычисляет частичную зависимость при 100 равномерно распределенных
точек X S или точек, указанных вами
используя аргумент пары имя-значение 'QueryPoints' .Вы можете указать
количество ( N ) наблюдений для выборки из данных предиктора с использованием
аргумент пары имя-значение 'NumObservationsToSample' .
Линейные графики и точечные диаграммы
Линейные графики и точечные диаграммы
Содержание
- Одна независимая и одна зависимая переменные
- Диаграмма рассеяния
- Линейный график
- Многолинейный график
Введение
Линейные графики — отличный способ отображать независимые и зависимые переменные, которые являются количественными.
Когда обе переменные являются количественными, отрезок линии, соединяющий две точки на графике, выражает наклон, которые можно визуально интерпретировать относительно наклона других линий или выражается в виде точной математической формулы. Диаграммы разброса похожи к линейным графикам, поскольку они начинаются с сопоставления точек количественных данных. Разница в том, что с диаграммой рассеяния принимается решение, что отдельные точки не должны напрямую соединяться линия, но вместо этого выражает тенденцию.Эту тенденцию можно увидеть прямо через распределение баллов или с добавлением линии регрессии. Статистический инструмент, используемый для математического выражения тенденции в данных.
Одна независимая и одна зависимая переменная
Точечная диаграмма
Линейный график
На диаграмме рассеяния отметка, обычно точка или маленький кружок, представляет
единая точка данных. С одной отметкой (точкой) для каждой точки данных визуальный
распределение данных можно увидеть.В зависимости от того, насколько плотно точки
вместе, вы сможете различить четкую тенденцию в данных.
С одной отметкой (точкой) для каждой точки данных визуальный
распределение данных можно увидеть.В зависимости от того, насколько плотно точки
вместе, вы сможете различить четкую тенденцию в данных.
Поскольку точки данных представляют собой реальные данные, собранные в лаборатории
установка, а не теоретически рассчитанные значения, они будут представлять
все ошибки, присущие такому процессу сбора. Линия регрессии
может использоваться для статистического описания тенденции точек в разбросе
график, чтобы помочь связать данные с теоретическим идеалом.Эта регрессия
линия выражает математическую связь между независимым и
зависимая переменная. В зависимости от программного обеспечения, используемого для создания регрессии
линии, вам также может быть дана константа, которая выражает « доброту
подгонка кривой. То есть, с какой степенью уверенности мы можем
говорят, что эта линия действительно описывает тенденцию в данных. Корреляционная
Константа обычно выражается как R 2 (R-квадрат). Будет ли эта регрессия
линия должна быть линейной или изогнутой в зависимости от того, что предсказывает ваша гипотеза
отношения есть.Когда используется изогнутая линия, это обычно выражается
как кривая второго порядка (кубическая) или третьего порядка (квадратичная). Выше
кривые порядка могут более точно соответствовать фактическим точкам данных, но редко
дать лучшее математическое описание взаимосвязи.
Корреляционная
Константа обычно выражается как R 2 (R-квадрат). Будет ли эта регрессия
линия должна быть линейной или изогнутой в зависимости от того, что предсказывает ваша гипотеза
отношения есть.Когда используется изогнутая линия, это обычно выражается
как кривая второго порядка (кубическая) или третьего порядка (квадратичная). Выше
кривые порядка могут более точно соответствовать фактическим точкам данных, но редко
дать лучшее математическое описание взаимосвязи.
Вернуться к началу
Линейные графики похожи на точечные диаграммы в том, что они записывают отдельные данные
значения в виде отметок на графике.Разница в том, что создается линия
соединяя каждую точку данных вместе. Таким образом, локальное изменение от
точка в точку можно увидеть. Это делается, когда важно уметь
чтобы увидеть локальное изменение между любыми парами точек. Общая тенденция
все еще можно увидеть, но к этой тенденции присоединяется местная тенденция между
отдельные или небольшие группы точек. В отличие от диаграмм рассеяния, независимые
переменная может быть скалярной или порядковой.В приведенном выше примере Месяц
можно рассматривать как скалярные или порядковые. Наклон линии
сегменты представляют интерес, но мы, вероятно, не будем генерировать математические
формулы для отдельных сегментов.
Общая тенденция
все еще можно увидеть, но к этой тенденции присоединяется местная тенденция между
отдельные или небольшие группы точек. В отличие от диаграмм рассеяния, независимые
переменная может быть скалярной или порядковой.В приведенном выше примере Месяц
можно рассматривать как скалярные или порядковые. Наклон линии
сегменты представляют интерес, но мы, вероятно, не будем генерировать математические
формулы для отдельных сегментов.
Приведенный выше пример можно было бы также создать в виде гистограммы. Ты бы используйте линейный график, если вы хотите более четко видеть скорость изменения (наклона) между отдельными точками данных. Если независимая переменная был номинальным, вы почти наверняка использовали бы гистограмму вместо линии график.
Вернуться к началу
Две (или более) независимых и одна зависимая переменная
Многолинейный график
Здесь мы взяли тот же график, что и выше, и добавили второй независимый
переменная, год. Обе независимые переменные, месяц и год, могут быть
рассматриваются как порядковые или скалярные. Это часто бывает с
большие единицы времени, такие как недели, месяцы и годы.Поскольку у нас есть
вторая независимая переменная, требуется какое-то кодирование, чтобы указать
какому уровню (году) соответствует каждая строка. Хотя мы могли пометить каждую полоску текстом
с указанием года, более эффективно использовать цвет и / или другой
символ на точках данных. Нам понадобится легенда, чтобы объяснить кодировку
схема.
Обе независимые переменные, месяц и год, могут быть
рассматриваются как порядковые или скалярные. Это часто бывает с
большие единицы времени, такие как недели, месяцы и годы.Поскольку у нас есть
вторая независимая переменная, требуется какое-то кодирование, чтобы указать
какому уровню (году) соответствует каждая строка. Хотя мы могли пометить каждую полоску текстом
с указанием года, более эффективно использовать цвет и / или другой
символ на точках данных. Нам понадобится легенда, чтобы объяснить кодировку
схема.
Многолинейные графики имеют характеристики экономии места по сравнению с сопоставимыми
сгруппированная гистограмма. Поскольку значения данных отмечены маленькими отметками (точками)
и не стержни, их не нужно смещать друг относительно друга (только когда
значения данных очень плотные, не становится ли это проблемой).Другое преимущество
состоит в том, что строки могут легко закодироваться двойным кодом. С линиями они оба могут
иметь цветовую маркировку (для компьютера и цветной печати) или форму с
символы (для черно-белого воспроизведения). С полосами, кодирование формы
нельзя использовать, и необходимо заменить кодирование по образцу. Кодирование паттернов
имеет тенденцию быть более ограничивающим.
С линиями они оба могут
иметь цветовую маркировку (для компьютера и цветной печати) или форму с
символы (для черно-белого воспроизведения). С полосами, кодирование формы
нельзя использовать, и необходимо заменить кодирование по образцу. Кодирование паттернов
имеет тенденцию быть более ограничивающим.
Обратите внимание на разрыв в строке данных 1996 года (зеленый / треугольник) между Август и октябрь.Поскольку данные за сентябрь отсутствуют, линию не следует подключать в период с августа по октябрь, поскольку это дают ошибочный местный уклон. Это особенно важно, если вы показываете линия без символов в отдельных точках данных.
Вернуться к началу
Советы Excel
Для получения информации о создании гистограмм в Excel перейдите в раздел Scatter
Модуль «Графики и линейные графики» или перейдите в Excel
Главное меню учебника с полным списком модулей.
Специальные советы для линейных графиков
- В руководстве по построению графиков даются конкретные инструкции по созданию разброса. графики и линии регрессии
- Линейные графики могут быть созданы либо с типом линейного графика, либо с (XY) Разброс. При использовании (XY) Scatter выберите Connected with Line подтип.
- Проще создать линейный график с разбросом (XY), когда ваши независимые а зависимые переменные — в столбцах.
- Метки для точек данных называются маркерами
- Цвет и размер линии и маркеров можно установить двойным щелчком на линии на графике.
- Маркеры можно отключить, дважды щелкнув строку и выбрав Нет под маркерами.
5.1 График частичной зависимости (PDP)
График частичной зависимости (PDP)
График частичной зависимости (короткий график PDP или PD) показывает предельное влияние, которое одна или две функции оказывают на прогнозируемый результат модели машинного обучения (Дж.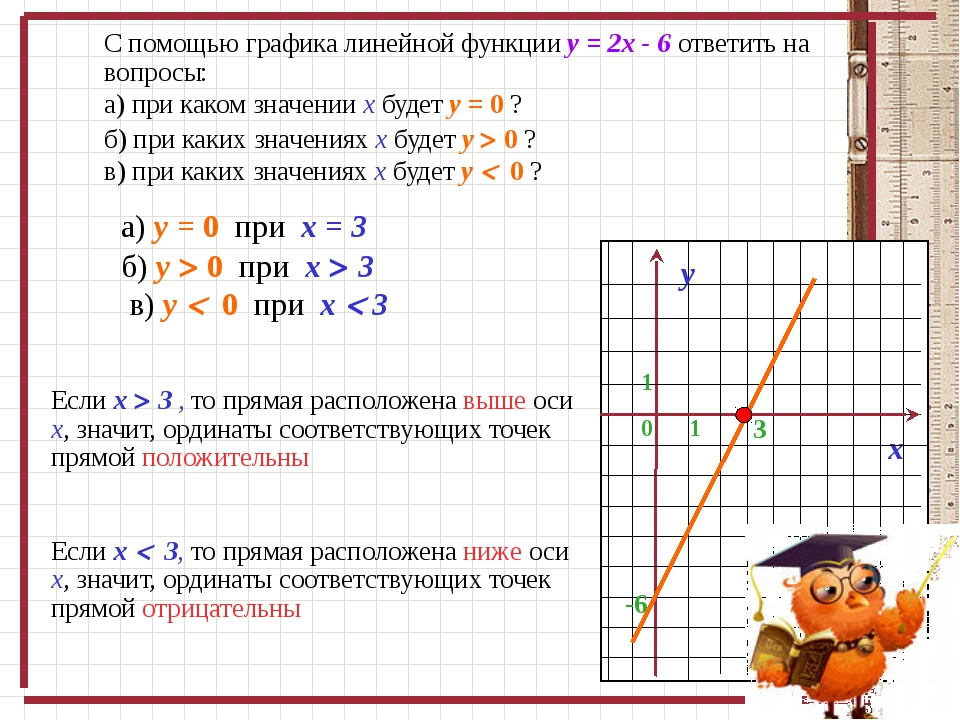 Х. Фридман 2001). График частичной зависимости может показать, является ли связь между целью и элементом линейной, монотонной или более сложной. Например, при применении к модели линейной регрессии графики частичной зависимости всегда показывают линейную зависимость.
Х. Фридман 2001). График частичной зависимости может показать, является ли связь между целью и элементом линейной, монотонной или более сложной. Например, при применении к модели линейной регрессии графики частичной зависимости всегда показывают линейную зависимость.
Функция частичной зависимости для регрессии определяется как:
\ [\ hat {f} _ {x_S} (x_S) = E_ {x_C} \ left [\ hat {f} (x_S, x_C) \ right] = \ int \ hat {f} (x_S, x_C) d \ mathbb {P} (x_C) \]
\ (x_S \) — это функции, для которых должна быть построена функция частичной зависимости, а \ (x_C \) — другие функции, используемые в модели машинного обучения \ (\ hat {f} \).Обычно в наборе S есть только одна или две функции. Функции в S — это те, для которых мы хотим знать влияние на прогноз. Векторы признаков \ (x_S \) и \ (x_C \) вместе составляют общее пространство признаков x. Частичная зависимость работает за счет маргинализации выходных данных модели машинного обучения по распределению функций в наборе C, так что функция показывает взаимосвязь между функциями в наборе S, которые нас интересуют, и прогнозируемым результатом. Путем маргинализации по сравнению с другими функциями мы получаем функцию, которая зависит только от функций в S, включая взаимодействие с другими функциями.{(i)} _ {C} \) — это фактические значения функций из набора данных для функций, которые нас не интересуют, а n — количество экземпляров в наборе данных. Предположение PDP состоит в том, что признаки в C не коррелируют с признаками в S. Если это предположение нарушается, средние значения, вычисленные для графика частичной зависимости, будут включать точки данных, которые очень маловероятны или даже невозможны (см. Недостатки).
Путем маргинализации по сравнению с другими функциями мы получаем функцию, которая зависит только от функций в S, включая взаимодействие с другими функциями.{(i)} _ {C} \) — это фактические значения функций из набора данных для функций, которые нас не интересуют, а n — количество экземпляров в наборе данных. Предположение PDP состоит в том, что признаки в C не коррелируют с признаками в S. Если это предположение нарушается, средние значения, вычисленные для графика частичной зависимости, будут включать точки данных, которые очень маловероятны или даже невозможны (см. Недостатки).
Для классификации, когда модель машинного обучения выводит вероятности, график частичной зависимости отображает вероятность для определенного класса при различных значениях для функции (ей) в S.Простой способ иметь дело с несколькими классами — нарисовать по одной линии или графику для каждого класса.
График частичной зависимости — это глобальный метод: метод рассматривает все экземпляры и дает утверждение о глобальной связи функции с прогнозируемым результатом.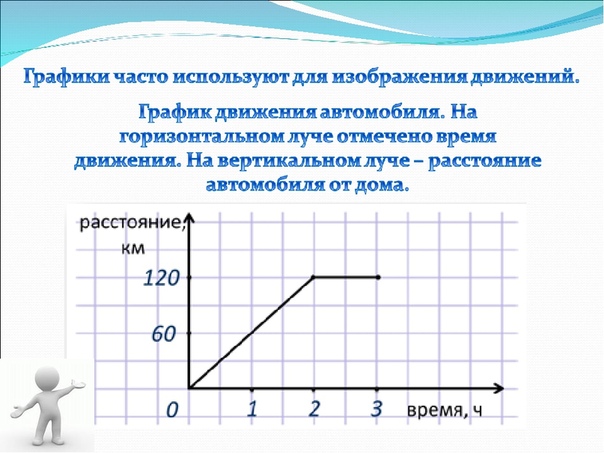
Категориальные признаки
До сих пор мы рассматривали только числовые характеристики. Для категориальных признаков частичную зависимость очень легко вычислить. Для каждой из категорий мы получаем оценку PDP, заставляя все экземпляры данных иметь одну и ту же категорию.Например, если мы смотрим на набор данных по аренде велосипедов и интересуемся графиком частичной зависимости для сезона, мы получаем 4 числа, по одному на каждый сезон. Чтобы вычислить значение для «лета», мы заменяем сезон всех экземпляров данных на «лето» и усредняем прогнозы.
Примеры
На практике набор объектов S обычно содержит только один объект или максимум два, потому что один объект создает 2D-графики, а два объекта создают 3D-графики. Все остальное довольно сложно.Даже 3D на двухмерной бумаге или мониторе — это уже сложная задача.
Вернемся к примеру регрессии, в котором мы прогнозируем количество велосипедов, которые будут взяты напрокат в данный день.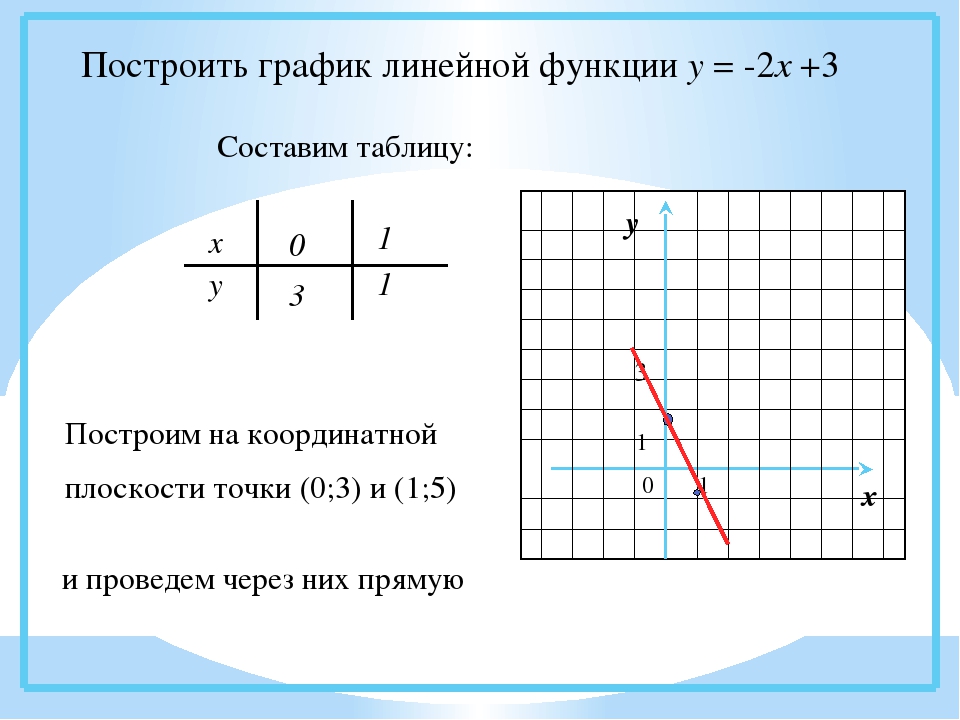 Сначала мы подбираем модель машинного обучения, а затем анализируем частичные зависимости. В этом случае мы подобрали случайный лес для прогнозирования количества велосипедов и использовали график частичной зависимости для визуализации отношений, которые модель усвоила. Влияние погодных условий на прогнозируемое количество велосипедов показано на следующем рисунке.
Сначала мы подбираем модель машинного обучения, а затем анализируем частичные зависимости. В этом случае мы подобрали случайный лес для прогнозирования количества велосипедов и использовали график частичной зависимости для визуализации отношений, которые модель усвоила. Влияние погодных условий на прогнозируемое количество велосипедов показано на следующем рисунке.
РИСУНОК 5.2: PDP для модели прогнозирования количества велосипедов, а также температуры, влажности и скорости ветра. Наибольшие различия видны в температуре. Чем жарче, тем больше берут напрокат. Эта тенденция достигает 20 градусов Цельсия, затем сглаживается и немного падает при 30. Отметки на оси абсцисс показывают распределение данных.
Для теплой, но не слишком жаркой погоды модель прогнозирует в среднем большое количество арендованных велосипедов. Потенциальным байкерам все чаще отказывают в аренде велосипеда, когда влажность превышает 60%.Кроме того, чем больше ветра, тем меньше людей любят кататься на велосипеде, что имеет смысл. Интересно, что прогнозируемое количество прокатов велосипедов не падает, когда скорость ветра увеличивается с 25 до 35 км / ч, но данных для обучения не так много, поэтому модель машинного обучения, вероятно, не сможет получить значимый прогноз для этого диапазона. По крайней мере, интуитивно я ожидал, что количество велосипедов будет уменьшаться с увеличением скорости ветра, особенно когда скорость ветра очень высока.
Интересно, что прогнозируемое количество прокатов велосипедов не падает, когда скорость ветра увеличивается с 25 до 35 км / ч, но данных для обучения не так много, поэтому модель машинного обучения, вероятно, не сможет получить значимый прогноз для этого диапазона. По крайней мере, интуитивно я ожидал, что количество велосипедов будет уменьшаться с увеличением скорости ветра, особенно когда скорость ветра очень высока.
Чтобы проиллюстрировать график частичной зависимости с категориальной характеристикой, мы исследуем влияние характеристики сезона на прогнозируемую аренду велосипедов.
РИСУНОК 5.3: PDP для модели прогнозирования количества велосипедов и сезона. Неожиданно все сезоны показывают одинаковый эффект на прогнозы модели, только на весну модель прогнозирует меньшее количество прокатов велосипедов.
Мы также вычисляем частичную зависимость для классификации рака шейки матки. На этот раз мы подобрали случайный лес, чтобы предсказать, может ли женщина заболеть раком шейки матки, на основе факторов риска.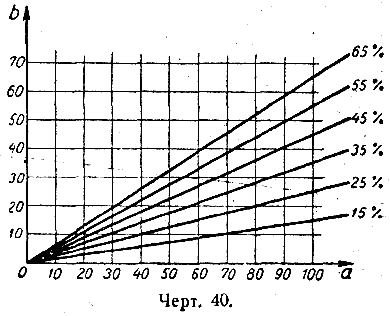 Мы вычисляем и визуализируем частичную зависимость вероятности рака от различных характеристик для случайного леса:
Мы вычисляем и визуализируем частичную зависимость вероятности рака от различных характеристик для случайного леса:
РИСУНОК 5.4: PDP вероятности рака в зависимости от возраста и лет с гормональными контрацептивами. Для возраста PDP показывает, что вероятность низкая до 40 лет и увеличивается после. Чем больше лет на гормональных контрацептивах, тем выше прогнозируемый риск рака, особенно после 10 лет. Для обеих функций было доступно не так много точек данных с большими значениями, поэтому оценки PD в этих регионах менее надежны.
Мы также можем визуализировать частичную зависимость сразу двух признаков:
РИСУНОК 5.5: PDP вероятности рака и взаимосвязь возраста и количества беременностей. График показывает увеличение вероятности рака в 45 лет. Для женщин младше 25 лет прогнозируемый риск рака ниже у женщин, у которых было 1 или 2 беременности, по сравнению с женщинами, у которых было 0 или более 2 беременностей. Но будьте осторожны, делая выводы: это может быть просто корреляция, а не причинная связь!
Преимущества
Вычисление графиков частичной зависимости является интуитивно понятным : Функция частичной зависимости для определенного значения признака представляет собой средний прогноз, если мы заставим все точки данных принять это значение признака. По моему опыту, непрофессионалы обычно быстро понимают идею PDP.
По моему опыту, непрофессионалы обычно быстро понимают идею PDP.
Если объект, для которого вы вычислили PDP, не коррелирует с другими функциями, то PDP прекрасно представляют, как этот объект влияет на прогноз в среднем. В некоррелированном случае интерпретация ясна. : График частичной зависимости показывает, как изменяется средний прогноз в вашем наборе данных при изменении j-го признака. Сложнее, когда функции коррелируют, см. Также недостатки.
Графики частичной зависимости легко реализовать .
Расчет графиков частичной зависимости имеет причинную интерпретацию . Мы вмешиваемся в функцию и измеряем изменения в прогнозах. При этом мы анализируем причинно-следственную связь между функцией и прогнозом. Связь является причинной для модели — потому что мы явно моделируем результат как функцию функций — но не обязательно для реального мира!
Недостатки
Реалистичное максимальное количество признаков в функции частичной зависимости равно двум. Это не вина PDP, а двумерного представления (бумага или экран), а также нашей неспособности представить более трех измерений.
Это не вина PDP, а двумерного представления (бумага или экран), а также нашей неспособности представить более трех измерений.
На некоторых графиках частичного разряда не отображается распределение признаков . Пропуск распределения может ввести в заблуждение, потому что вы можете переоценить регионы, в которых почти нет данных. Эту проблему легко решить, показав коврик (индикаторы точек данных на оси x) или гистограмму.
Допущение независимости — самая большая проблема с графиками ВД.Предполагается, что признак (и), для которого вычисляется частичная зависимость, не коррелирован с другими признаками. Например, предположим, что вы хотите предсказать, насколько быстро человек ходит, учитывая его вес и рост. Для частичной зависимости одного из признаков, например рост, мы предполагаем, что другие характеристики (вес) не связаны с ростом, что, очевидно, является ложным предположением. Для вычисления PDP на определенной высоте (например, 200 см) мы усредняем предельное распределение веса, которое может включать вес ниже 50 кг, что нереально для человека 2 метра.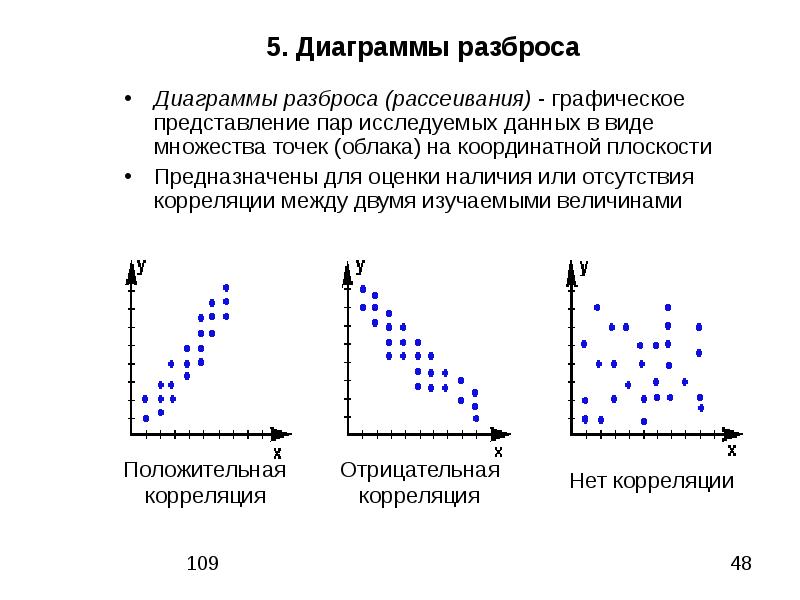 Другими словами: когда функции коррелированы, мы создаем новые точки данных в областях распределения функций, где фактическая вероятность очень мала (например, маловероятно, что кто-то ростом 2 метра, но весит менее 50 кг). Одним из решений этой проблемы являются графики накопленного локального эффекта или короткие графики ALE, которые работают с условным вместо предельного распределения.
Другими словами: когда функции коррелированы, мы создаем новые точки данных в областях распределения функций, где фактическая вероятность очень мала (например, маловероятно, что кто-то ростом 2 метра, но весит менее 50 кг). Одним из решений этой проблемы являются графики накопленного локального эффекта или короткие графики ALE, которые работают с условным вместо предельного распределения.
Гетерогенные эффекты могут быть скрыты , потому что графики частичного разряда показывают только средние предельные эффекты.Предположим, что для функции половина ваших точек данных имеет положительную связь с прогнозом — чем больше значение функции, тем больше прогноз, — а другая половина имеет отрицательную связь — чем меньше значение функции, тем больше прогноз. Кривая частичного разряда может быть горизонтальной линией, поскольку эффекты обеих половин набора данных могут нейтрализовать друг друга. Затем вы делаете вывод, что функция не влияет на прогноз. Построив отдельные кривые условного ожидания вместо агрегированной линии, мы можем выявить неоднородные эффекты.
Программное обеспечение и альтернативы
Существует ряд пакетов R, реализующих PDP. Я использовал для примеров пакет iml , но есть также pdp или DALEX . В Python графики частичной зависимости встроены в scikit-learn , и вы можете использовать PDPBox .
Альтернативами PDP, представленными в этой книге, являются графики ALE и кривые ICE.
Графики и уравнения двух переменных
Декартова система
Декартова система координат используется для визуализации точек на графике путем отображения расстояний между точками по двум осям.
Цели обучения
Объясните, как наносить точки на декартовую плоскость и что это значит.
Основные выводы
Ключевые моменты
- Декартова система координат — это 2-мерная плоскость с горизонтальной осью, известной как [latex] x [/ latex] -ось, и вертикальной осью, известной как [latex] y [/ latex]-осью.

- В декартовой системе координат каждая точка однозначно определяется на плоскости с парой числовых координат, каждая из которых является расстоянием со знаком от точки до одной из двух осей.
- Числовые координаты точки представлены упорядоченной парой [latex] (x, y) [/ latex], где координата [latex] x [/ latex] — это расстояние точки от [latex] y [/ latex] -ось, а координата [latex] y [/ latex] — это расстояние от [latex] x [/ latex] -оси.
- Декартова система координат разбита на четыре квадранта, обозначенных I, II, III и IV, начиная с верхнего правого угла и двигаясь против часовой стрелки.
- Независимая переменная находится на оси [latex] x [/ latex] и состоит из входных значений.Зависимая переменная находится на оси [latex] y [/ latex] и состоит из выходных значений.
Ключевые термины
- независимая переменная : произвольный ввод; в декартовой плоскости значение [латекс] х [/ латекс].
- Ось Y : ось на графике, которая обычно рисуется снизу вверх, причем значения растут дальше вверх.

- квадрант : Одна из четырех четвертей декартовой плоскости, ограниченная осью [latex] x [/ latex] и осью [latex] y [/ latex].
- зависимая переменная : произвольный вывод; в декартовой плоскости значение [латекс] y [/ латекс].
- Ось x : ось на графике, который обычно строится слева направо со значениями, увеличивающимися вправо.
- упорядоченная пара : набор, содержащий ровно два элемента в фиксированном порядке, используемый для представления точки в декартовой системе координат. Обозначение: [latex] (x, y) [/ latex].
Декартова система координат, названная в честь «отца аналитической геометрии», французского математика XVII века Рене Декарта, представляет собой двумерную плоскость с горизонтальной осью и вертикальной осью.Обе оси простираются до бесконечности, а стрелки используются для обозначения бесконечной длины. Горизонтальная ось известна как ось [latex] x [/ latex], а вертикальная ось — как ось [latex] y [/ latex]. Точка пересечения осей называется началом координат.
Точка пересечения осей называется началом координат.
Декартова система координат используется для построения точек. Точки задаются однозначно в декартовой плоскости парой числовых координат, которые представляют собой расстояния со знаком от точки до двух осей. Каждая точка может быть представлена упорядоченной парой [latex] (x, y) [/ latex], где координата [latex] x [/ latex] — это расстояние точки от оси [latex] y [/ latex]. а координата [latex] y [/ latex] — это расстояние от оси [latex] x [/ latex].Таким образом, точка пересечения двух осей — [латекс] (0,0) [/ латекс]. На оси [latex] x [/ latex] числа увеличиваются вправо и уменьшаются влево; на оси [latex] y [/ latex] числа увеличиваются при движении вверх и уменьшаются при движении вниз.
Декартова система координат: Декартова система координат с нанесенными 4 точками, включая начало координат, в [latex] (0,0) [/ latex].
Точки графика
Чтобы построить точку [latex] (2,3) [/ latex], например, вы начинаете с начала координат (где две оси пересекаются).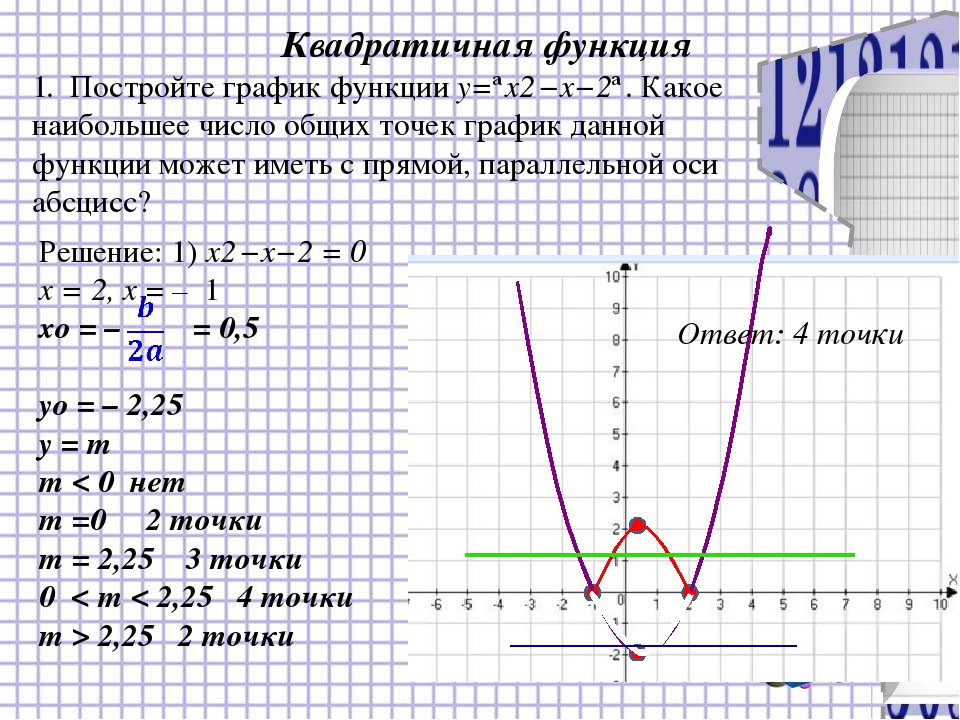 Затем переместите три юнита вправо и два вверх.
Затем переместите три юнита вправо и два вверх.
Точка [латекс] (- 3,1) [/ latex] находится путем перемещения трех единиц влево от начала координат и одной единицы вверх.
Нецелочисленные координаты [latex] (- 1.5, -2.5) [/ latex] лежат между -1 и -2 на оси [latex] x [/ latex] и между -2 и -3 на [latex ] y [/ latex] -ось. Следовательно, вы перемещаете полторы единицы влево и две с половиной единицы вниз.
Независимые и зависимые переменные
Декартова плоскость особенно полезна для построения серии точек, которые показывают взаимосвязь между двумя переменными.
Например, существует связь между количеством машин, которые моет автомойка, и деньгами, которые приносит бизнес (его доходом). Выручка или объем производства зависят от количества машин или материалов, которые они моют. Таким образом, доход — это зависимая переменная ([latex] y [/ latex]), а количество автомобилей — независимая переменная ([latex] x [/ latex]). Выручка отображается по оси [латекс] y [/ латекс], а количество вымытых автомобилей — по оси [латекс] x [/ латекс].
Квадранты
Декартова система координат разбита на четыре квадранта по двум осям.Эти квадранты обозначены I, II, III и IV, начиная с верхнего правого угла и продолжая против часовой стрелки, как показано ниже.
Декартовы координаты: Четыре квадранта декартовой системы координат. Стрелки на осях указывают, что они бесконечно продолжаются в своих направлениях.
Некоторые основные правила, касающиеся этих квадрантов, могут быть полезны для быстрого построения точек:
- Квадрант I: точки имеют положительные координаты [латекс] x [/ латекс] и [латекс] y [/ латекс], [латекс] (x, y) [/ латекс].
- Квадрант II: Точки имеют отрицательные [латекс] x [/ латекс] и положительные [латекс] y [/ латекс] координаты, [латекс] (- x, y) [/ latex].
- Квадрант III: Точки имеют отрицательные координаты [latex] x [/ latex] и [latex] y [/ latex], [latex] (- x, -y) [/ latex].
- Квадрант IV: Точки имеют положительные [латекс] x [/ латекс] и отрицательные [латекс] y [/ латекс] координаты, [латекс] (x, -y) [/ latex].

- Точки, которые имеют значение 0 для любой координаты, лежат на самих осях и не считаются находящимися ни в одном из квадрантов (например,г., [латекс] (4,0) [/ латекс], [латекс] (0, -2) [/ латекс]).
Уравнения с двумя переменными
Уравнения с двумя неизвестными представляют собой взаимосвязь между двумя переменными и имеют ряд решений.
Цели обучения
Объясните, что представляет собой уравнение с двумя переменными
Основные выводы
Ключевые моменты
- Уравнение с двумя переменными имеет ряд решений, которые удовлетворяют уравнению для обеих переменных.
- Каждое решение уравнения с двумя переменными представляет собой упорядоченную пару и может быть записано в форме [латекс] (x, y) [/ latex].
Ключевые термины
- Декартовы координаты : координаты точки, измеренные от начала координат по горизонтальной оси слева направо (ось [latex] x [/ latex]) и по вертикальной оси снизу вверх ([latex ] y [/ latex] -ось).

- упорядоченная пара : набор, содержащий ровно два элемента в фиксированном порядке, используемый для представления точки в декартовой системе координат.Обозначение: [latex] (x, y) [/ latex].
Уравнения с двумя неизвестными представляют собой взаимосвязь между двумя переменными. Уравнения с двумя переменными часто выражают взаимосвязь между переменными [latex] x [/ latex] и [latex] y [/ latex], которые соответствуют декартовым координатам.
Уравнения с двумя переменными имеют не одно решение, а серию решений, которые удовлетворяют уравнению для обеих переменных. Каждое решение представляет собой упорядоченную пару и может быть записано в виде [латекс] (x, y) [/ latex].
Решение уравнений с двумя переменными
Для данного уравнения с двумя переменными выбор значения одной переменной определяет, каким будет значение другой переменной. Другими словами, если предоставляется значение для одной переменной, то можно найти решение, удовлетворяющее уравнению. Это достигается заменой данного значения на эту переменную и вычислением значения другой.
Это достигается заменой данного значения на эту переменную и вычислением значения другой.
Пример 1
Рассмотрим следующее уравнение:
[латекс] y = 2x [/ латекс]
Это уравнение с двумя переменными, которое имеет бесконечное количество решений.Для любого значения [latex] x [/ latex] соответствующее значение [latex] y [/ latex] будет в два раза больше его значения.
Например, [латекс] (1, 2) [/ латекс] является решением уравнения. Это можно проверить, указав значения [latex] x [/ latex] и [latex] y [/ latex]:
[латекс] (2) = 2 (1) [/ латекс]
Другое решение — [латекс] (30, 60) [/ латекс], потому что [латекс] (60) = 2 (30) [/ латекс]. Таким образом, существует бесконечное количество упорядоченных пар, удовлетворяющих уравнению. [Latex] [/ latex]
Пример 2
Теперь рассмотрим следующее уравнение:
[латекс] y = 2x + 4 [/ латекс]
Является ли точка [латекс] (3, 10) [/ латекс] решением этого уравнения?
Обратите внимание, что упорядоченная пара [latex] (3, 10) [/ latex] сообщает нам, что [latex] x = 3 [/ latex] и [latex] y = 10 [/ latex]. Чтобы оценить, является ли это решением уравнения, подставьте эти значения вместо переменных следующим образом:
Чтобы оценить, является ли это решением уравнения, подставьте эти значения вместо переменных следующим образом:
[латекс] (10) = 2 (3) + 4 [/ латекс]
[латекс] 10 = 6 + 4 [/ латекс]
Это верное утверждение, поэтому [latex] (3, 10) [/ latex] действительно является решением этого уравнения.
Пример 3
Решите уравнение [латекс] y = 4x — 7 [/ latex] для значения [latex] x = 3 [/ latex].
Решение данного уравнения могло бы иметь форму [latex] (x, y) [/ latex], и нам дается значение [latex] x [/ latex].Значение [latex] x [/ latex] можно подставить в уравнение, чтобы найти значение [latex] y [/ latex] в этой точке:
[латекс] y = 4 (3) — 7 [/ латекс]
[латекс] y = 12 — 7 [/ латекс]
[латекс] y = 5 [/ латекс]
Для данного уравнения [латекс] y = 5 [/ латекс], когда [латекс] x = 3 [/ латекс]. Следовательно, решение — [латекс] (3, 5) [/ латекс].
Пример 4
Решите [латекс] x + 2y = 8 [/ latex] для [latex] x = 4 [/ latex].
Как и в приведенном выше примере, предоставляется значение [latex] x [/ latex], и нам нужно найти соответствующее значение [latex] y [/ latex].Сначала мы можем переписать уравнение в виде [латекс] y [/ латекс]:
[латекс] x + 2y -x = 8 -x [/ латекс]
[латекс] 2y = 8 — x [/ латекс]
[латекс] \ dfrac {2y} {2} = \ dfrac {8-x} {2} [/ латекс]
[латекс] y = \ dfrac {8} {2} — \ dfrac {x} {2} [/ латекс]
[латекс] y = 4 — \ dfrac {1} {2} x [/ латекс]
Теперь подставьте [латекс] x = 4 [/ latex] в уравнение и решите относительно [latex] y [/ latex]:
[латекс] y = 4 — \ dfrac {1} {2} (4) [/ латекс]
[латекс] y = 4 — 2 [/ латекс]
[латекс] y = 2 [/ латекс]
Раствор [латекс] (4, 2) [/ латекс].
Графические уравнения
Уравнения и их отношения могут быть визуализированы в виде графиков различных типов.
Цели обучения
Практика построения графиков уравнений в декартовой плоскости
Основные выводы
Ключевые моменты
- Графики — важные инструменты для визуализации уравнений.

- Чтобы построить уравнение, выберите значение для [latex] x [/ latex] или [latex] y [/ latex], найдите переменную, которую вы не выбрали, изобразите упорядоченную пару как точку на декартовой плоскости , и повторяйте, пока у вас не будет нанесено достаточно точек, чтобы вы могли соединить их для визуализации графика.
Ключевые термины
- график : диаграмма, отображающая данные; в частности, тот, который показывает взаимосвязь между двумя или более величинами, измерениями или числами.
- точка : объект, имеющий местоположение в пространстве или на плоскости, но не имеющий экстента.
Теперь, когда мы знаем, что такое уравнения, как нам их визуализировать? Для уравнения с двумя переменными, [latex] x [/ latex] и [latex] y [/ latex], нам нужен график с двумя осями: ось [latex] x [/ latex] и [latex] y. [/ latex] -ось.Мы будем использовать декартову плоскость, в которой ось [latex] x [/ latex] является горизонтальной линией, а ось [latex] y [/ latex] — вертикальной линией. Место пересечения двух осей называется началом координат.
Место пересечения двух осей называется началом координат.
Построение уравнения с двумя переменными
Начнем со следующего уравнения:
[латекс] y = 2x-3 [/ латекс]
Мы начнем с выбора нескольких значений [latex] x [/ latex], их включения в это уравнение и решения для неизвестной переменной [latex] y [/ latex]. После создания нескольких упорядоченных пар [latex] x [/ latex] и [latex] y [/ latex], мы построим их на декартовой плоскости и соединим точки.
Для трех значений [latex] x [/ latex] давайте выберем отрицательное число, ноль и положительное число, чтобы мы включили точки с обеих сторон оси [latex] y [/ latex]:
- Если [латекс] x = -2 [/ латекс], то [латекс] y = -7 [/ латекс]. Рисуем точку [латекс] (- 2, -7) [/ латекс].
- Если [латекс] x = 0 [/ латекс], то [латекс] y = -3 [/ латекс]. Рисуем точку [латекс] (0, -3) [/ латекс].
- Если [латекс] x = 2 [/ латекс], то [латекс] y = 1 [/ латекс]. Рисуем точку [латекс] (2,1) [/ латекс].
 {2} = 100 [/ латекс]
{2} = 100 [/ латекс]Давайте разберемся, выбрав несколько точек для построения графика.{2}} & = \ sqrt {100} \\ y & = \ pm10 \ end {align} [/ latex]
Итак, мы строим [латекс] (0,10) [/ латекс] и [латекс] (0, -10) [/ латекс].
Обратите внимание, что нам не всегда нужно выбирать значения для [latex] x [/ latex]. Например, давайте теперь попробуем установить [latex] y = 0 [/ latex].
Используя ту же арифметику, что и выше, мы получаем упорядоченные пары [латекс] (10,0) [/ латекс] и [латекс] (- 10,0) [/ латекс]. Постройте их также.
У нас все еще недостаточно очков, чтобы действительно понять, что происходит, поэтому давайте выберем еще несколько.2 + 9 [/ latex]: Этот график представляет собой параболу (открытая U-образная кривая, симметричная относительно линии). Параболы могут открываться вверх или вниз, вправо или влево; у них также есть максимальное или минимальное значение.
Графики уравнений как графики решений
Решение уравнения может быть нанесено на графики, чтобы лучше визуализировать поведение уравнения или функции.

Цели обучения
Осознайте, что графическое отображение уравнения включает графическое представление его решений
Основные выводы
Ключевые моменты
- Чтобы решить уравнение, нужно найти, какие значения (числа, функции, множества и т. Д.)) удовлетворяют условию, сформулированному в форме уравнения.
- После того, как уравнение построено в виде графика, решения для любого конкретного значения [latex] x [/ latex] или [latex] y [/ latex] можно легко найти, просто взглянув на график.
- Чтобы найти переменную в уравнении, вы должны использовать алгебраические манипуляции, чтобы получить переменную сама по себе на одной стороне уравнения (обычно слева).
Ключевые термины
- уравнение : Утверждение, что два выражения эквивалентны (например,г., [латекс] х = 5 [/ латекс]).
- график : диаграмма, отображающая данные, обычно представляющие взаимосвязь между двумя или более величинами.

- выражение : расположение символов, обозначающих значения, выполняемые над ними операции и группирующие символы (например, [latex] (2x + 4) [/ latex]).
В математике решить уравнение — значит найти, какие значения (числа, функции, множества и т. Д.) Удовлетворяют условию, сформулированному в форме уравнения (два выражения, связанных равенством).Каждое из выражений содержит одно или несколько неизвестных.
Какая графическая разница между уравнениями с одной переменной и уравнениями с двумя переменными?
Графики линейных уравнений с одной переменной
Линейное уравнение с одной переменной может быть записано в форме [latex] ax + b = 0, [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] — действительные числа, а [latex] ] а \ neq 0 [/ латекс]. В уравнении, где [latex] x [/ latex] является действительным числом, график представляет собой набор всех упорядоченных пар с любым значением [latex] y [/ latex] в паре с этим действительным числом для [latex] x [/ латекс].

Например, для построения графика уравнения [латекс] x-1 = 0, [/ latex] несколько упорядоченных пар будут включать:
- [латекс] (1, -3) [/ латекс]
- [латекс] (1, -2) [/ латекс]
- [латекс] (1, -1) [/ латекс]
- [латекс] (1,0) [/ латекс]
- [латекс] (1,1) [/ латекс]
- [латекс] (1,2) [/ латекс]
- [латекс] (1,3) [/ латекс]
Их также можно найти, решив уравнение графика для [латекс] x [/ латекс], которое дает [латекс] x = 1 [/ латекс].Это означает, что значения [latex] y [/ latex] точек не имеют значения, пока их значения [latex] x [/ latex] равны 1. Таким образом, график представляет собой вертикальную линию, проходящую через эти точки, поскольку все точки имеют одинаковое значение [latex] x [/ latex].
То же самое верно и для уравнения, записанного, например, как [латекс] ay + b = 0 [/ latex] или [latex] y = -4 [/ latex]. График представляет собой горизонтальную линию, проходящую через точки, у которых все значения [latex] y [/ latex] равны -4.
 3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является полиномом 3-й степени, называемым кубическим полиномом. .
3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является полиномом 3-й степени, называемым кубическим полиномом. .Графическое изображение неравенств
Решения неравенств можно изобразить, нарисовав граничную линию, разделяющую координатную плоскость пополам, и заштриховав одну из этих частей.
Цели обучения
Попрактикуйтесь в графическом изображении неравенств путем закрашивания в нужном сечении плоскости
Основные выводы
Ключевые моменты
- Все решения данного неравенства расположены в одной полуплоскости и могут быть изобразены.
- Чтобы изобразить неравенство, сначала рассмотрите его как линейное уравнение и нанесите на график соответствующую линию.Затем закрасьте правильную полуплоскость, чтобы представить все возможные решения неравенства.
- Если в неравенстве используется символ [латекс] \ leq [/ latex] или [латекс] \ geq [/ latex], граничная линия должна быть сплошной, что означает, что решения включают точки на самой линии.

- Если в неравенстве используется символ [latex] <[/ latex] или [latex]> [/ latex], граничная линия должна быть нарисована пунктирной линией, что означает, что решения не включают никаких точек на линии.
Ключевые термины
- полуплоскость : одна из двух частей координатной плоскости, созданная при рисовании линии.
- граничная линия : прямая линия на графике неравенства, определяющая полуплоскость, содержащую решения неравенства.
В нашем исследовании линейных уравнений с двумя переменными мы заметили, что все решения уравнения — а только этих решений — были расположены на графике этого уравнения. Теперь мы хотим определить расположение решений линейных неравенств с двумя переменными.
Линейные неравенства двух переменных имеют одну из следующих форм:
- [латекс] ac + by
- [латекс] ac + by \ leq c [/ латекс]
- [латекс] ac + by> c [/ латекс]
- [латекс] ac + by \ geq c [/ латекс]
Напомним, что для линейного уравнения с двумя переменными упорядоченные пары, которые дают истинные утверждения при подстановке в уравнение, называются «решениями» этого уравнения.

Мы можем сделать аналогичное утверждение относительно неравенств по двум переменным. Мы говорим, что неравенство с двумя переменными имеет решение, если была найдена пара значений, такая что замена этих значений в неравенство приводит к истинному утверждению.
Как и в случае с уравнениями, решения линейных неравенств имеют определенные местоположения в координатной плоскости. При линейном равенстве двух переменных все решения расположены в одной цельной полуплоскости. Прямая линия, проведенная через плоскость, делит плоскость на две полуплоскости, как показано на схеме ниже.Показанная прямая линия называется граничной линией.
Полуплоскости: показанная выше линия границы делит координатную плоскость на две полуплоскости.
Например, рассмотрим следующее неравенство:
[латекс] 2x + 3y \ leq 6 [/ латекс]
График ниже демонстрирует все решения этого неравенства, которые попадают на граничную линию и в заштрихованную полуплоскость.
График [латекс] 2x + 3y \ leq 6 [/ latex]: Все точки, лежащие на граничной линии и в заштрихованной полуплоскости, являются решениями этого неравенства.

Теперь рассмотрим следующее неравенство:
[латекс] y> 2 [/ латекс]
На приведенном ниже графике показаны решения этого неравенства: заштрихованная область над линией границы. Обратите внимание: поскольку в неравенстве используется символ [latex]> [/ latex], а не символ [latex] \ geq [/ latex], неравенство строгое: точки на граничной линии не являются решениями, поэтому линия проводится пунктирный.
График [latex] y> 2 [/ latex] : Все точки в заштрихованной полуплоскости над линией являются решениями этого неравенства.
Метод построения графиков линейных неравенств от двух переменных заключается в следующем.
Сначала рассмотрите неравенство как уравнение (т.е. замените знак неравенства знаком равенства) и нанесите это уравнение на график. Это называется пограничной линией. Примечание:
- Если выполняется неравенство [латекс] \ leq [/ latex] или [латекс] \ geq [/ latex], нарисуйте сплошную линию границы.
 Это означает, что точки на линии являются решениями и являются частью графика.
Это означает, что точки на линии являются решениями и являются частью графика. - Если выполняется неравенство [латекс] <[/ латекс] или [латекс]> [/ латекс], нарисуйте линию границы пунктиром.Это означает, что точки на линии не являются решениями и не являются частью графика.
Определите, какую полуплоскость затенить, выбрав контрольную точку.
- Если при замене контрольная точка дает истинное утверждение, закрасьте содержащую ее полуплоскость.
- Если при подстановке контрольная точка дает ложное утверждение, закрасьте полуплоскость на противоположной стороне линии границы.
Пример 1
Изобразите следующее неравенство:
[латекс] 3x — 2y \ geq -4 [/ латекс]
Во-первых, нам нужно построить граничную линию.Для этого рассмотрим неравенство как уравнение:
[латекс] 3x − 2y = −4 [/ латекс]
Напомним, что для построения графика уравнения мы можем подставить значение одной переменной и решить для другой.
 Полученная упорядоченная пара будет одним решением уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение:
Полученная упорядоченная пара будет одним решением уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение:[латекс] \ begin {align} 3 (0) — 2y & = -4 \\ — 2y & = -4 \\ \ dfrac {-2y} {- 2} & = \ dfrac {-4} {- 2 } \\ y & = 2 \ end {align} [/ latex]
Теперь заменим [latex] y = 0 [/ latex], чтобы найти другое решение:
[латекс] \ begin {align} 3x — 2 (0) & = — 4 \\ 3x & = -4 \\ \ dfrac {3x} {3} & = \ dfrac {-4} {3} \\ x & = — \ dfrac {4} {3} \ end {align} [/ latex]
Теперь мы можем построить график двух известных решений: [latex] (0, 2) [/ latex] и [latex] (- \ frac {4} {3}, 0) [/ latex].Неравенство [латекс] \ geq [/ латекс], поэтому мы знаем, что нам нужно нарисовать линию сплошной. Это дает граничную линию ниже:
График граничной линии для [латекс] 3x — 2y \ geq -4 [/ latex]: График граничной линии, построенный с использованием двух решений для упорядоченных пар.
Затем выберите контрольную точку, чтобы выяснить, какую полуплоскость нам нужно затенять.
 Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим вместо [latex] (0, 0) [/ latex] в исходное неравенство:
Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим вместо [latex] (0, 0) [/ latex] в исходное неравенство:[латекс] \ begin {align} 3 (0) — 2 (0) & \ geq -4 \\ 0 & \ geq -4 \ end {align} [/ latex]
Это верное утверждение, поэтому тень в полуплоскости, содержащая [латекс] (0, 0).[/ латекс]
График [latex] 3x — 2y \ geq -4 [/ latex]: График, показывающий все возможные решения данного неравенства. Решения лежат в заштрихованной области, включая граничную линию.
Графический анализ и отображение данных
Графический анализ и отображение данных Кармен Джунта, Le Moyne CollegeОбъект
Графики можно использовать для отображения больших объемов числовых данных и для изображения взаимосвязей между числовыми значениями различных переменных.Их также можно использовать для получения количественных соотношений между переменными. Это упражнение даст студентам возможность попрактиковаться в построении графиков, четко отображающих экспериментальные данные.
Предпосылки: графики и количественные данные
Передача и даже просмотр информации о числовых данных можно улучшить с помощью графического дисплея. Например, вопросы о закономерностях в данных и изменении одной переменной при изменении другой часто легче увидеть на графике, чем в таблице.В случае химической периодичности — повторяющихся подъемов и падений химических свойств с атомным номером, который составляет основу периодической таблицы — графическое представление показывает взаимосвязи, которые в противном случае могли бы быть не очевидны. На графике ниже показано, как одно свойство элементов, молярный объем, увеличивается и уменьшается с атомным номером. Обратите внимание, что пики — это элементы, которые попадают в тот же столбец в современной таблице.
Рис. 1. График молярного объема (мл на моль атомов) элементарных твердых частиц по сравнению сатомный номер. Обратите внимание, что все пики на этом графике относятся к щелочным металлам.На рис. 1 показан пример графика xy , который иногда также называют диаграммой рассеяния или линейным графиком.
 Это наиболее распространенный формат для построения научных данных, поскольку он отображает взаимосвязь между двумя переменными. Другие распространенные форматы графиков включают столбчатую диаграмму , показанную на рис.2 (и тесно связанный столбчатый график, в котором используются вертикальные, а не горизонтальные полосы) и круговая диаграмма , показанная на рис.3. Столбчатые и столбчатые диаграммы часто используются для отображения значений одной величины, измеренной для разных образцов, когда образцы различаются по типу, а не по количеству.
Это наиболее распространенный формат для построения научных данных, поскольку он отображает взаимосвязь между двумя переменными. Другие распространенные форматы графиков включают столбчатую диаграмму , показанную на рис.2 (и тесно связанный столбчатый график, в котором используются вертикальные, а не горизонтальные полосы) и круговая диаграмма , показанная на рис.3. Столбчатые и столбчатые диаграммы часто используются для отображения значений одной величины, измеренной для разных образцов, когда образцы различаются по типу, а не по количеству.
Рисунок 2. Масса азота, полученная из различных источников, содержащаяся в стандартном стеклянном шаре.Рисунок 2 показывает массу газообразного азота, содержащегося в определенном стеклянном шаре; метки на вертикальной оси обозначают различные методы приготовления образца. Обратите внимание, как простой взгляд на эту простую диаграмму четко разделяет образцы на два набора со слегка, но определенно разными значениями.

Диаграмма 3. Потребление энергии в США по секторам в 1999 г.На рисунке 3 показано потребление энергии в США в различных секторах энергетики в процентах от общего потребления. Круговые диаграммы особенно хорошо подходят для отображения разделения целого на небольшое количество частей.
Оставшаяся часть этого упражнения будет сосредоточена на графиках xy. График xy используется для отображения взаимосвязи между двумя переменными. На рис. 1 переменными являются атомный номер (Z) и молярный объем (V).Каждая точка на этом графике представляет собой упорядоченную пару данных: для каждого значения Z есть соответствующее значение V. Каждое значение Z нанесено на горизонтальную ось, также называемую осью x или абсциссой , и осью соответствующее значение V откладывается по вертикальной оси, также называемой осью y или ординатой . На рис. 4 показано, как это делается с точкой для элемента скандий: Z = 21 и V = 15,0 мл / моль.
 Точка расположена на 21 единицу правее оси y (то есть на 21 единицу по оси x ) и 15 единиц.0 единиц над осью x (то есть 15,0 единиц по оси y ). Переменная, построенная по оси x , называется независимой переменной ; переменная, построенная по оси y , называется зависимой переменной . Перед нанесением данных на график часто бывает удобно перечислить данные в двух столбцах. Один содержит значения независимых переменных, обычно в числовом порядке; другой содержит соответствующие значения зависимых переменных.
Точка расположена на 21 единицу правее оси y (то есть на 21 единицу по оси x ) и 15 единиц.0 единиц над осью x (то есть 15,0 единиц по оси y ). Переменная, построенная по оси x , называется независимой переменной ; переменная, построенная по оси y , называется зависимой переменной . Перед нанесением данных на график часто бывает удобно перечислить данные в двух столбцах. Один содержит значения независимых переменных, обычно в числовом порядке; другой содержит соответствующие значения зависимых переменных.
Рисунок 4.Построение точки Z = 21, V = 15.0.Построим график из данных, которые можно собрать в эксперименте. Эксперимент требует измерения температуры жидкости через равные промежутки времени по мере того, как жидкость охлаждается и в конечном итоге затвердевает. (Точка замерзания жидкости может быть определена с помощью таких измерений с последующим тщательным графическим анализом.) Данные показаны в следующей таблице. (Обратите внимание, что данные отображаются в том виде, в котором они были собраны наиболее вероятно.Время здесь является независимой переменной, поскольку оно проходит независимо. С интервалом в одну минуту экспериментатор записывал температуру, зависимую переменную, соответствующую текущему истекшему времени.) Данные также лучше всего строить по порядку: сначала переместите нулевые единицы по оси x (то есть прямо по оси y. ), а затем на 90,0 единиц до построения первой точки. Теперь вернитесь в начало координат (где пересекаются оси) и переместите на 1 единицу вправо (по оси x) и на 87,7 единиц вверх (рис. 5a).
Таблица 1. Данные по охлаждению жидкого нафталина.время (мин) температура (° C) 0 90.0 1 87,7 2 84,8 3 83,1 4 81,8 5 79,8 6 80,0 7 80,1 8 80,1 9 80,1 10 80.1 11 79,8 12 79,7 13 79,4 14 78,3 15 74,0 16 69,3 17 66,0 График завершается нанесением остальных точек таким же образом, рисованием плавной кривой по данным, маркировкой осей и присвоением графику названия.Полный график показан на рис. 5б.
Рисунок 5. a) Построение первых двух точек из таблицы 1.
б) Заполненный график.Метки осей являются важной особенностью информативного графика . Они должны указать имя переменной, нанесенной на каждую ось, и единицы измерения переменной. Заголовок также часто необходим, чтобы сделать график информативным. Заголовок не должен просто повторять метки осей (например, «температура vs.времени »), но должен содержать некоторую информацию о системе, к которой относится график. Например,« охлаждение нафталина »сообщает читателю о процессе (охлаждение) и образце (нафталин). Если отчет содержит несколько графиков, включающих одних и тех же переменных, тогда названия графиков важны. Например, если бы Рис. 5b появился в эксперименте, где были измерены несколько кривых охлаждения, необходимо было бы отличать эту кривую охлаждения от других по названиям (например, нафталин в одном заголовке и антрацен в другом или чистый нафталин в одном названии и раствор нафталина в другом).
Рисунок 5b представляет собой хорошо построенный график во всех отношениях, кроме одного: данные не распределены по всей поверхности графика. Установка масштаба должна быть первым шагом в построении графика. Оставьте место внизу, слева и вверху графика для меток осей, числовых шкал и заголовка. Считайте остальную часть миллиметровой бумаги полем, на котором вы нанесете свои точки. Подсчитайте количество больших прямоугольников вдоль каждой оси. В нашем примере четыре прямоугольника расположены вдоль оси x (время) и три — вдоль оси y (температура).Теперь посмотрите на данные и определите минимальное и максимальное значения, которые нужно отобразить. Временные данные находятся в диапазоне от 0 до 17 минут, данные о температуре от 66,0 до 90,0 градусов. Теперь установите масштаб так, чтобы данные распределялись по полю. Как? Выберите «круглые» числа, в которые помещаются данные и которые легко делятся на количество доступных полей. Например, временные данные соответствуют диапазону от 0 до 20 минут, а диапазон 20 минут легко делится на четыре доступных поля, в результате чего каждый большой ящик стоит 5 минут.По оси Y данные попадают в диапазон от 60 до 90 градусов, и этот диапазон (который составляет 30 градусов «в высоту») делится на три доступных поля. (Примечание: график не обязательно должен содержать точку 0,0.)
Прямолинейные графики и линейные уравнения
Рис. 6. a) Лист бумаги перед нанесением данных из таблицы 1. Обратите внимание на место для меток и заголовков осей. Каждый из четырех больших квадратов на горизонтальной оси представляет 5-минутные интервалы. Каждый из трех больших прямоугольников по вертикальной оси представляет интервалы в 10 градусов.
б) Завершенный график с разбросом данных.
Графики также могут играть не только роль отображения при анализе количественных данных. В частности, когда точки данных падают на прямую линию или очень близко к ней, тогда уравнение этой линии может использоваться для связи отображаемых переменных. Например, см. Рисунок 7. Были проведены измерения светопоглощения нескольких растворов, содержащих известную молярность брома (Br 2 ). Поглощение наносили на график зависимости от молярности брома обычным способом, за исключением того, что линия здесь не соединяет точки данных.Скорее, он представляет собой «наилучшую» прямую линию, соответствующую данным: это прямая линия, которая проходит через все точки данных или рядом с ними. Ожидается, что на графике зависимости поглощения от концентрации будет прямая линия, поскольку поглощение света обычно прямо пропорционально концентрации. Если график должен давать прямую линию, то можно вывести формулу, которая связывает отображаемые переменные.На рис. 7 уравнение и линия были определены компьютерной программой; тем не менее, процесс может быть выполнен вручную с разумным приближением.Сначала нужно построить точки данных обычным способом. Затем проводят прямую линию «сквозь» данные; используйте линейку или линейку, чтобы провести линию, проходящую рядом или через все точки данных. Наконец, определите формулу прямой линии, измерив ее наклон и точку пересечения оси y . Наклон (m) прямой — это изменение y по сравнению с изменением x: m = Δy / Δx.
Пересечение оси y (b) — это значение, при котором линия пересекает ось y, или, более технически, координата y линии, где ее координата x равна нулю.Как только наклон m и точка пересечения оси y b известны, формула для прямой или линейной связи между переменными x и y будет простой:
y = mx + b.
Рисунок 7. Калибровочная кривая для эксперимента с использованием видимой спектроскопии. Диагональная линия — это наиболее подходящая прямая линия, проходящая через данные, а уравнение — это формула для этой линии. Жирные пунктирные линии — это направляющие линии для измерения уклона.На рис. 7 измерьте наклон линии.Для этого выберите две точки на линии (примечание: не две экспериментальные точки, а точки на линии; в конце концов, линия определяется всеми экспериментальными точками, поэтому она использует все данные). В принципе, не имеет значения, какие точки на линии вы выберете, но с практической точки зрения удобно выбирать точки, которые проходят через линии сетки или рядом с ними. Кроме того, точки, расположенные далеко друг от друга на линии, дают более точный наклон, чем точки, расположенные близко друг к другу. Рисунок 7 отмечен жирными пунктирными линиями, чтобы помочь нам найти наклон на основе точки в правом верхнем углу и одной в нижнем левом углу наиболее подходящей линии.Разница в координатах y составляет 1,11 — 0,10 = 1,01 единицы оптической плотности, а разница в координатах x составляет 0,0090 — 0,0010 = 0,0080 моль / л, поэтому наклон равен:
m = Δy / Δx = 1.01 / (0.0080 моль / л) = 126 л / моль.
Обратите внимание, что наклон имеет единицы измерения, которые зависят от единиц измерения осей графика. Чтобы найти точку пересечения y, протяните прямую линию наилучшего соответствия до оси y, если она еще не пересекает ее. Обратите внимание, что линия не полностью проходит через начало координат; скорее, он пересекает ось y примерно в 0.1 ед. Ниже нуля. Таким образом, точка пересечения по оси Y равна b = -0,1. (Примечание: b имеет те же единицы измерения, что и ось y, в этом примере это чистое число.) Итак, формула этой наиболее подходящей линии:y = (126 л / моль) x — 0,1.
Наконец, используя символы, более выразительные для наших реальных переменных (абсорбция и молярность, а не общие x и y), мы пишем:A = (126 л / моль) [Br 2 ] — 0,1,
очень близко к компьютерному уравнению.Иногда цель эксперимента заключается в нахождении наклона или пересечения наиболее подходящей линии, поскольку наклон имеет физическое значение.В других случаях наиболее подходящее уравнение будет полезно для дальнейшего анализа данных. Например, уравнение, полученное на рис. 7 может быть решена для молярностей брома:
[Br 2 ] = (A + 0,1) / (126 л / моль).
Эта формула может быть полезной для определения молярности неизвестных растворов путем измерения их оптической плотности.Процедура подготовки графика xy
1. Нарисуйте оси, оставив достаточно места для меток осей, числовых масштабов и заголовка.
Топоры нарисуйте линейкой или линейкой. Нарисуйте эти прямые линии немного выше низа и немного правее левого края страницы. (Обратите внимание, что «нижняя часть» может быть короткой или длинной стороной листа бумаги размером 8 1 / 2 x 11 дюймов; вы можете свободно ориентировать график в книжной или альбомной ориентации.) Оставьте место под ось x для числового масштаба и метки оси x; оставьте место слева от оси y для ее числового масштаба и метки оси y.Оставьте немного места вверху для заголовка графика.2. Определите переменные x и y.
Какая переменная должна быть нанесена по какой оси? Независимая переменная откладывается по горизонтальной оси (x), а зависимая переменная — по вертикальной оси (y). Итак, какая переменная является зависимой, а какая независимой? Если в инструкциях указано «построить ___ vs. ___», первая переменная является зависимой (y) переменной, а вторая — независимой (x). Другими словами, стандартная инструкция — «график y vs.x. «Если у вас нет явных инструкций, то независимая переменная обычно находится под экспериментальным контролем (например, время или известные концентрации в наших предыдущих примерах), а зависимая переменная — как свойство, которое измеряется в эксперименте. (например, температура и оптическая плотность выше).3. Установите числовую шкалу так, чтобы точки данных были распределены по всему графику. Графики становятся проще и точнее, когда точки данных рассредоточены по большой площади.Очевидно, труднее различать точки, нанесенные близко друг к другу на небольшом пространстве, и по той же причине труднее построить точки точно, если они должны быть расположены вместе. Установка шкалы подробно описана выше. При определении масштаба пронумеруйте оси соответственно.
4. Пометьте оси.
Этикетки должны включать название количества (например, время, температуру, оптическую плотность и т. Д.) И единицу измерения, выраженную аббревиатурой стандартной единицы (например,г., мин., ° C и т. д.).5. Организуйте точки данных и нанесите их на график.
Если ваши данные еще не представлены в виде таблицы, такой как таблица 1, соберите данные в такую таблицу, указав показания независимых переменных в числовом порядке. Постройте точки, как показано на рис. 4 и окружающий текст. Сделайте символ графика большим и достаточно четким, чтобы его можно было легко увидеть на миллиметровой бумаге. Для нарисованных от руки графиков хорошо подходят символы x или +, поскольку они показывают точную точку (а именно точку пересечения) как часть более крупного символа; точки в кружках также являются хорошими символами.6. Проведите линию или кривую «сквозь» данные.
Рис. 8. Точки данных с плавной кривой, проведенной «сквозь» их, и с соединяющими их отрезками линии.Как лучше всего представить построенные данные с помощью линии или кривой, зависит от нескольких обстоятельств, включая точность точек данных и известные или теоретические отношения между переменными. Обычно хорошей практикой является рисование плавной кривой «сквозь» данные (то есть через нанесенные точки или рядом с ними). В экспериментах, которые мы проводим по вводной химии, оборудование, методы и навыки, которые мы используем, обычно недостаточно точны, чтобы требовать, чтобы кривая проходила буквально через каждую точку данных; следовательно, график, соединяющий экспериментальные точки (соединяющий точки), равен , а не .В частности, не соединяет точки прямыми отрезками. (См. Рис. 8.) Иногда эксперимент включает построение графиков переменных, которые должны быть связаны уравнением прямой линии. Если это так, то «кривая», которую следует нарисовать, является наилучшей прямой линией, проходящей через данные или рядом с ними.
7. Дайте графику название.
Хорошие заголовки графиков позволяют различать похожие графики в отчете (указывая, к какому образцу или веществу относится каждый из них). Информативный заголовок предоставляет информацию, отличную от меток осей.
[1] По материалам Norman E. Griswold, «MISC 408: Графическое представление данных», Модульная лабораторная программа по химии.
Вернуться к расписанию лаборатории химических принципов.Графический праймер
Ученые любят говорить, что «независимая» переменная идет по оси абсцисс (нижняя, горизонтальная единица), а «зависимая» переменная идет по оси ординат (левая, вертикальная). Это не означает, что переменная x не тусуется, а переменная y скулит о переменной x никогда не быть рядом — это созависимость, а это совсем другое дело.
Когда вы говорите о переменных, «независимый» означает, что исследователь (вы или кто-то еще в белом халате) может выбрать любое значение, которое он / она хочет для этой переменной. Использование расстояния просмотра телевизора данных, вы можете представить, как исследователь кладет небольшие кусочки ленты на пол и размещает ее маленькие экспериментальные объекты на правильном расстоянии … тогда как я не могу думать ни о чем исследователь может напрямую контролировать, насколько зрение потеряли дети.
Лично я до сих пор путаю направо и налево и нахожу слова «зависимый» а «независимый» немного сбивает с толку. Поэтому я думаю, что «причина» (переменная x) и «следствие» (переменная y Переменная). Это не совсем верно и может вызвать у некоторых ученых апоплексический удар, но как своего рода помощь памяти, это может вам тоже помочь. Итак,
• Причина в том, насколько далеко ребенок сидит от телевизора — переменная x
• Эффект заключается в том, насколько она теряет зрение — переменная y.
Хорошо, теперь вы попробуете: для каждой пары, что такое «x», а где «y»?
Хорошо, эти двое были легкими.В обоих случаях переменные x (температура в резервуаре или количество еды дано) легко контролируются экспериментатором. Иногда переменная «x» не может фактически контролируются, но только «выбираются» исследователем — это особенно случай, когда некоторая версия «времени» является переменной x.
Однако будьте осторожны. Тот факт, что переменная включает время, не означает, что она автоматически переменная x. Иногда количество времени, которое занимает процесс, является ЭФФЕКТИВОМ лечения, и тогда это переменная «y».
Вы получили пример с Дилаудином? В этом случае исследователь пытается выяснить, сколько времени потребуется для облегчения боли В ЗАВИСИМОСТИ от количества принимаемого лекарства. Исследователь может напрямую контролировать (или выбрать) дозировку, а не время.
Наконец, таблицы данных часто содержат много столбцов, поэтому важно выяснить, какие из них принадлежат графику. Ниже введите «n» для данных, которые НЕ будут представлены ни «x», ни «y».
Авторские права Мэрилендского университета, 2007 г.
Вы можете ссылаться на этот сайт в образовательных целях.
Пожалуйста, не копируйте без разрешения
запросов / вопросов / отзывов, электронная почта: [email protected]
Как построить диаграмму рассеяния в Excel
В этом руководстве вы узнаете, как построить точечную диаграмму в Excel для создания графического представления двух коррелированных наборов данных.
Что вы видите при просмотре двух столбцов количественных данных в электронной таблице Excel? Всего два набора цифр. Вы хотите увидеть, как эти два набора связаны друг с другом? Диаграмма рассеяния — идеальный выбор для этого.
Точечная диаграмма в Excel
Диаграмма рассеяния (также называемая диаграммой XY или диаграммой рассеяния ) — это двухмерная диаграмма, которая показывает взаимосвязь между двумя переменными.
На точечной диаграмме и горизонтальная, и вертикальная оси представляют собой оси значений, на которых отображаются числовые данные. Как правило, независимая переменная находится на оси x, а зависимая переменная — на оси y. На диаграмме отображаются значения на пересечении осей x и y, объединенные в отдельные точки данных.
Основная цель диаграммы рассеяния — показать, насколько сильна взаимосвязь или корреляция между двумя переменными. Чем точнее точки данных располагаются по прямой линии, тем выше корреляция.
Как расположить данные для диаграммы рассеивания
Благодаря множеству встроенных шаблонов диаграмм, предоставляемых Excel, создание точечной диаграммы превращается в парочку кликов. Но сначала вам нужно правильно расположить исходные данные.
Как уже упоминалось, диаграмма рассеяния отображает две взаимосвязанные количественные переменные.Итак, вы вводите два набора числовых данных в два отдельных столбца.
Для простоты использования независимая переменная должна находиться в левом столбце , поскольку этот столбец будет нанесен на ось x. Зависимая переменная (та, на которую влияет независимая переменная) должна находиться в правом столбце , и она будет нанесена на ось y.
Наконечник. Если ваш зависимый столбец стоит перед независимым столбцом и вы не можете изменить его на листе, вы можете поменять местами оси x и y прямо на диаграмме.В нашем примере мы собираемся визуализировать взаимосвязь между рекламным бюджетом за определенный месяц (независимая переменная) и количеством проданных товаров (зависимая переменная), поэтому мы располагаем данные соответствующим образом:
Как создать диаграмму рассеяния в Excel
Если исходные данные правильно организованы, для построения диаграммы рассеяния в Excel необходимо выполнить два быстрых шага:
- Выберите два столбца с числовыми данными, включая заголовки столбцов. В нашем случае это диапазон C1: D13.Не выбирайте другие столбцы, чтобы не запутать Excel.
- Перейдите на вкладку Inset > группу Chats , щелкните значок диаграммы Scatter и выберите нужный шаблон. Чтобы вставить классический точечный график, щелкните первую миниатюру:
Диаграмма рассеяния будет немедленно вставлена в ваш рабочий лист:
В принципе можно считать проделанную работу. Или вы можете настроить некоторые элементы вашего графика, чтобы он выглядел более красивым и более четко передавал корреляцию между двумя переменными.
Типы точечных диаграмм
Помимо классической диаграммы рассеяния, показанной в приведенном выше примере, доступно еще несколько шаблонов:
- Scatter с плавными линиями и маркерами
- Scatter с плавными линиями
- Скаттер с прямыми линиями и маркерами
- Скаттер с прямыми линиями
Scatter с линиями лучше всего использовать, когда у вас мало точек данных. Например, вот как можно представить данные за первые четыре месяца с помощью диаграммы рассеяния с плавными линиями и маркерами:
Шаблоны графиков Excel XY также могут рисовать каждую переменную отдельно , представляя те же отношения по-разному.Для этого следует выделить 3 столбца с данными — крайний левый столбец с текстовыми значениями (метками) и два столбца с числами.
В нашем примере синие точки обозначают стоимость рекламы, а оранжевые точки обозначают проданные товары:
Чтобы просмотреть все доступные типы разброса в одном месте, выберите данные, щелкните значок разброс (X, Y) на ленте, а затем щелкните Дополнительные диаграммы разброса… Откроется диалоговое окно Inset Chart с выбран тип XY (Scatter) , и вы переключаетесь между различными шаблонами вверху, чтобы увидеть, какой из них обеспечивает наилучшее графическое представление ваших данных:
Трехмерная диаграмма рассеяния
В отличие от классической диаграммы рассеяния XY, трехмерная диаграмма рассеяния отображает точки данных на трех осях (x, y и z), чтобы показать взаимосвязь между тремя переменными.Поэтому его часто называют графиком XYZ .
К сожалению, нет возможности создать трехмерную диаграмму рассеяния в Excel даже в новой версии Excel 2019. Если вам очень нужен этот тип диаграммы для анализа данных, рассмотрите возможность использования стороннего инструмента, например plot.ly. На приведенном ниже снимке экрана показано, какой трехмерный график разброса может нарисовать этот инструмент:
График рассеяния и корреляция
Чтобы правильно интерпретировать диаграмму рассеяния, необходимо понимать, как переменные могут соотноситься друг с другом.Всего существует три типа корреляции:
Положительная корреляция — по мере увеличения переменной x увеличивается и переменная y. Примером сильной положительной корреляции является количество времени, которое студенты проводят за учебой, и их оценки.
Отрицательная корреляция — по мере увеличения переменной x переменная y уменьшается. Отказ от уроков и оценок отрицательно коррелируют — по мере увеличения количества пропусков экзаменационные баллы снижаются.
Нет корреляции — нет очевидной связи между двумя переменными; точки разбросаны по всей области диаграммы.Например, кажется, что между ростом и оценками учащихся нет никакой корреляции, поскольку первое никак не влияет на вторые.
Настройка диаграммы рассеяния XY в Excel
Как и в случае с другими типами диаграмм, почти каждый элемент точечной диаграммы в Excel можно настроить. Вы можете легко изменить заголовок диаграммы, добавить заголовки осей, скрыть линии сетки, выбрать собственные цвета диаграммы и многое другое.
Ниже мы сосредоточимся на нескольких настройках, относящихся к диаграмме рассеяния.
Отрегулируйте масштаб оси (уменьшите пустое пространство)
Если точки данных сгруппированы вверху, внизу, справа или слева от графика, вы можете удалить лишнее пустое пространство.
Чтобы уменьшить расстояние между первой точкой данных и вертикальной осью и / или между последней точкой данных и правым краем графика, выполните следующие действия:
- Щелкните правой кнопкой мыши по оси x и выберите Ось формата…
- На панели «Ось формата » установите требуемые границы минимум и максимум соответственно.
- Кроме того, вы можете изменить единицы Major , которые контролируют расстояние между линиями сетки.
На скриншоте ниже показаны мои настройки:
Чтобы удалить пространство между точками данных и верхним / нижним краями области графика, отформатируйте вертикальную ось Y аналогичным образом.
Добавить метки к точкам данных точечной диаграммы
При создании точечного графика с относительно небольшим количеством точек данных вы можете пометить точки по имени, чтобы сделать визуальный элемент более понятным. Вот как это сделать:
- Выберите график и нажмите кнопку Chart Elements .
- Отметьте поле Data Labels , щелкните маленькую черную стрелку рядом с ним, а затем щелкните Дополнительные параметры…
- На панели Format Data Labels перейдите на вкладку Label Options (последняя) и настройте метки данных следующим образом:
- Выберите поле «Значение из ячеек », а затем выберите диапазон, из которого вы хотите извлечь метки данных (в нашем случае B2: B6).
- Если вы хотите отображать только имена, снимите флажок X Value и / или Y Value , чтобы удалить числовые значения из меток.
- Укажите положение меток, В нашем примере выше точек данных.
Вот и все! Все точки данных на нашем графике рассеяния в Excel теперь помечены по имени:
. Совет: как исправить перекрывающиеся меткиКогда две или более точки данных находятся очень близко друг к другу, их метки могут перекрываться, как в случае с метками января и марта на нашей диаграмме разброса. Чтобы исправить это, щелкните метки, а затем нажмите перекрывающуюся, чтобы была выбрана только эта метка.Наведите курсор мыши на выбранную метку, пока курсор не изменится на четырехстороннюю стрелку, а затем перетащите метку в желаемое положение.
В результате у вас будет красивый график рассеяния Excel с хорошо читаемыми надписями:
Добавьте линию тренда и уравнение
Чтобы лучше визуализировать взаимосвязь между двумя переменными, вы можете нарисовать линию тренда на диаграмме разброса Excel, также называемую линией наилучшего соответствия .
Для этого щелкните правой кнопкой мыши любую точку данных и выберите Добавить линию тренда… из контекстного меню.
Excel проведет линию как можно ближе ко всем точкам данных, чтобы над линией было столько точек, сколько показано ниже.
Кроме того, вы можете показать уравнение для линии тренда , которое математически описывает взаимосвязь между двумя переменными. Для этого отметьте поле Display Equation on Chart на панели Format Trendline , которая должна появиться в правой части окна Excel сразу после добавления линии тренда.Результат этих манипуляций будет выглядеть примерно так:
То, что вы видите на скриншоте выше, часто называют графиком линейной регрессии , и вы можете найти подробные инструкции по его созданию здесь: Как создать график линейной регрессии в Excel.
Как поменять местами оси X и Y на диаграмме рассеивания
Как уже упоминалось, диаграмма рассеяния обычно отображает независимую переменную на горизонтальной оси и зависимую переменную на вертикальной оси.Если ваш график построен по-другому, самое простое решение — поменять местами исходные столбцы на листе, а затем нарисовать диаграмму заново.
Если по какой-либо причине переупорядочение столбцов невозможно, вы можете переключать серии данных X и Y прямо на диаграмме. Вот как:
- Щелкните правой кнопкой мыши любую ось и выберите Выбрать данные… в контекстном меню.
- В диалоговом окне Select Data Source нажмите кнопку Edit .
- Скопируйте значения X серии в поле значений Y серии и наоборот.
Наконечник. Для безопасного редактирования содержимого полей Series поместите указатель мыши в поле и нажмите F2.
- Дважды щелкните ОК , чтобы закрыть оба окна.
В результате ваша диаграмма рассеяния Excel претерпит следующее преобразование:
Вот как вы создаете диаграмму рассеяния в Excel. В нашем следующем руководстве мы продолжим эту тему и покажем, как быстро найти и выделить определенную точку данных на диаграмме разброса.

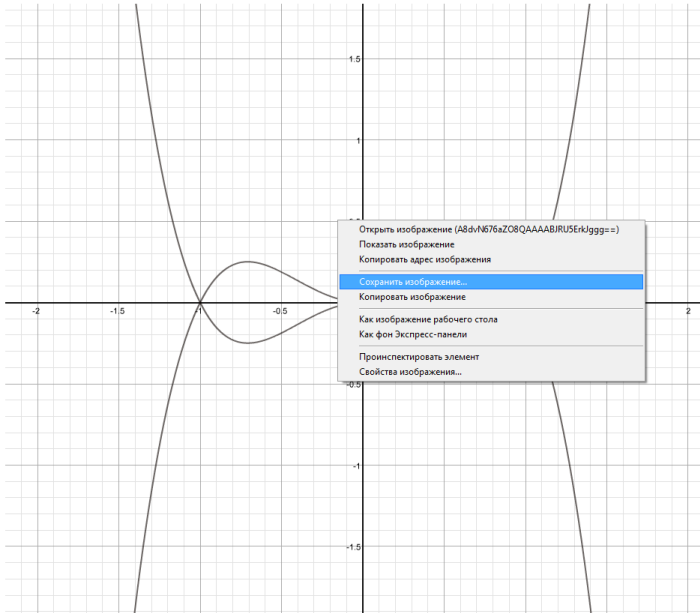
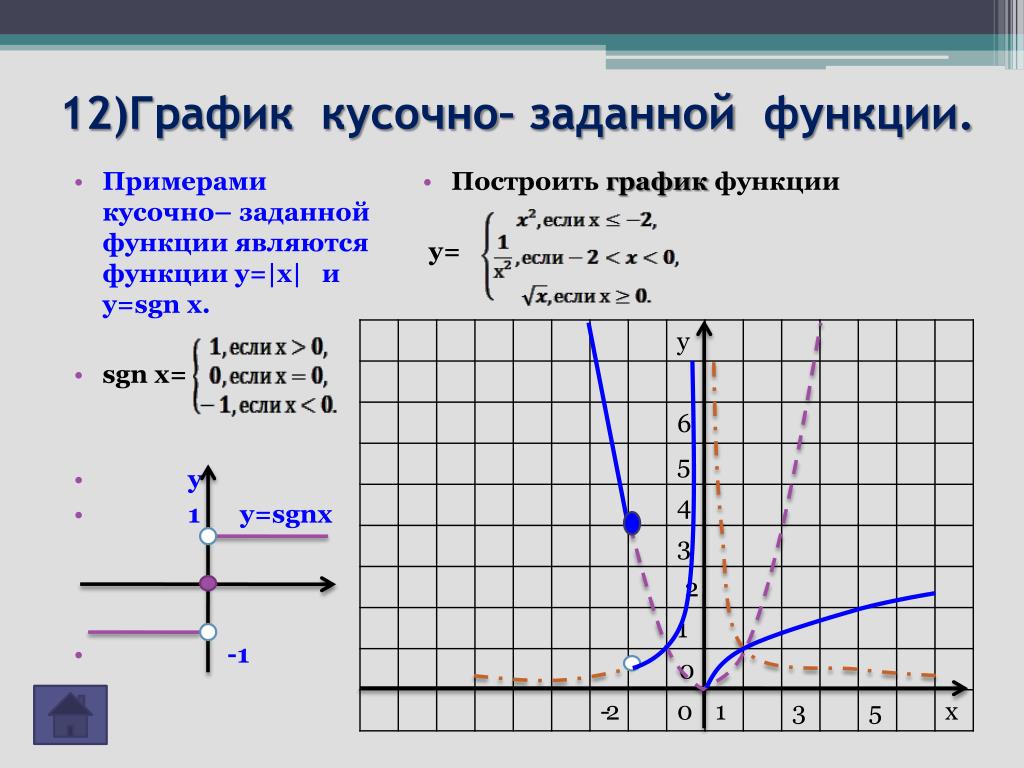 png» — задает имя выходоного файла, в случае если выбран соответствующий режим в set terminal
png» — задает имя выходоного файла, в случае если выбран соответствующий режим в set terminal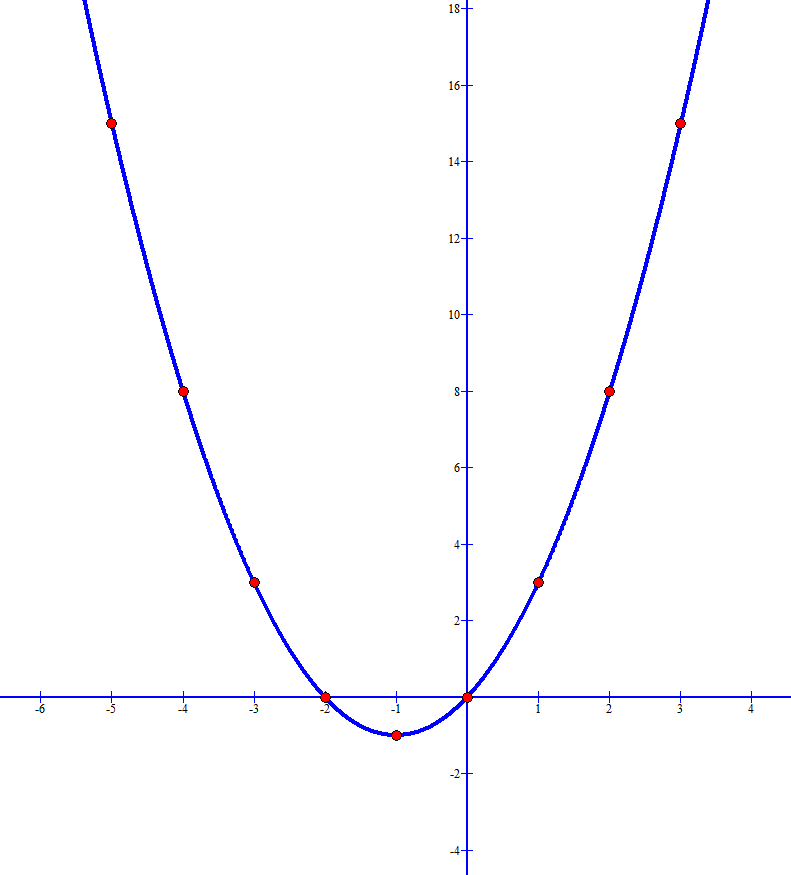 draw()
draw()
 Есть какие-нибудь предложения по Java…
Есть какие-нибудь предложения по Java…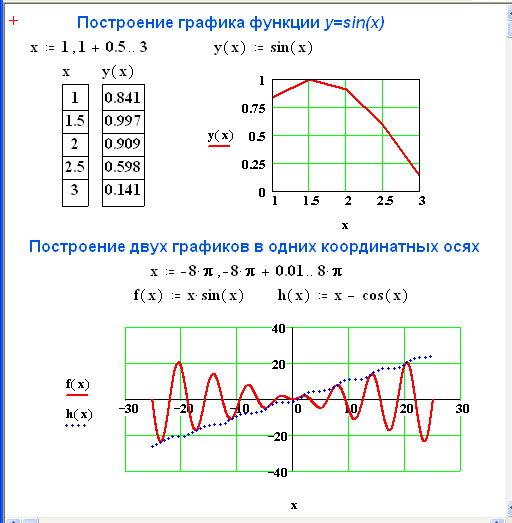 2)
def _generate_data(self): # function looped every 0.2 second to read or produce data
"""
Loop starting with the simulation start, getting data and
pushing it to the graph every 0.2 seconds
"""
# concatenate data on the time x-axis
self.xdata = jk.core.add_datapoint(self.xdata, time.time(), xnptsmax=self.mygraph.xnptsmax)
# concatenate data on the fake data y-axis
self.ydata = jk.core.add_datapoint(self.ydata, np.random.random(), xnptsmax=self.mygraph.xnptsmax)
self.mygraph.set_xydata(t, self.ydata)
t = test()
t.start()
t.stop()
2)
def _generate_data(self): # function looped every 0.2 second to read or produce data
"""
Loop starting with the simulation start, getting data and
pushing it to the graph every 0.2 seconds
"""
# concatenate data on the time x-axis
self.xdata = jk.core.add_datapoint(self.xdata, time.time(), xnptsmax=self.mygraph.xnptsmax)
# concatenate data on the fake data y-axis
self.ydata = jk.core.add_datapoint(self.ydata, np.random.random(), xnptsmax=self.mygraph.xnptsmax)
self.mygraph.set_xydata(t, self.ydata)
t = test()
t.start()
t.stop()
 ..
.. vbar(x='time', width = 0.5*60*60*50 ,bottom='open', top='close',fill_color='color', line_color='black', source = candle_data)
doc.add_root(column([plot]))
doc.add_periodic_callback(update, 20000)
doc.title = "Candle Data Live Rates"
vbar(x='time', width = 0.5*60*60*50 ,bottom='open', top='close',fill_color='color', line_color='black', source = candle_data)
doc.add_root(column([plot]))
doc.add_periodic_callback(update, 20000)
doc.title = "Candle Data Live Rates"
 Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.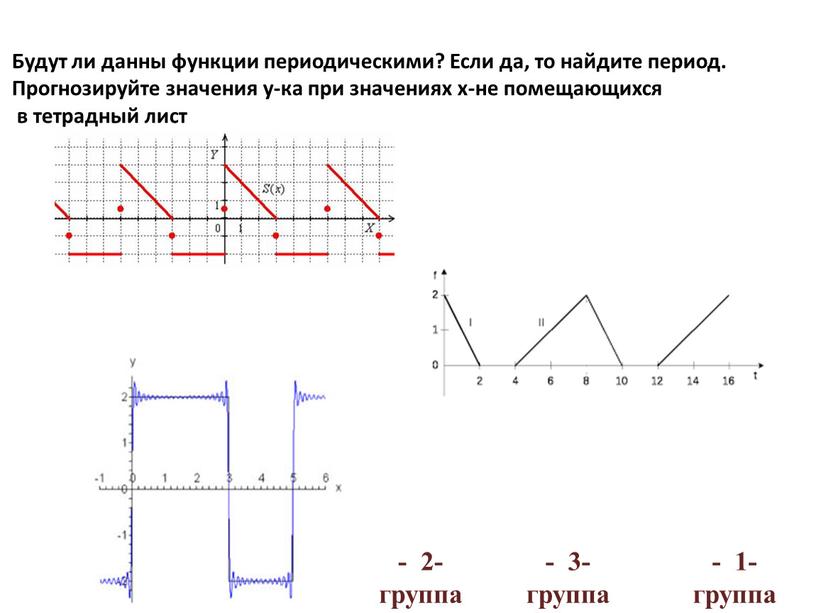
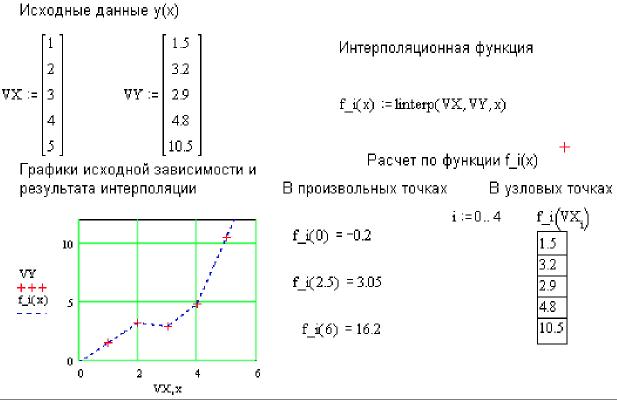


 е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47). Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.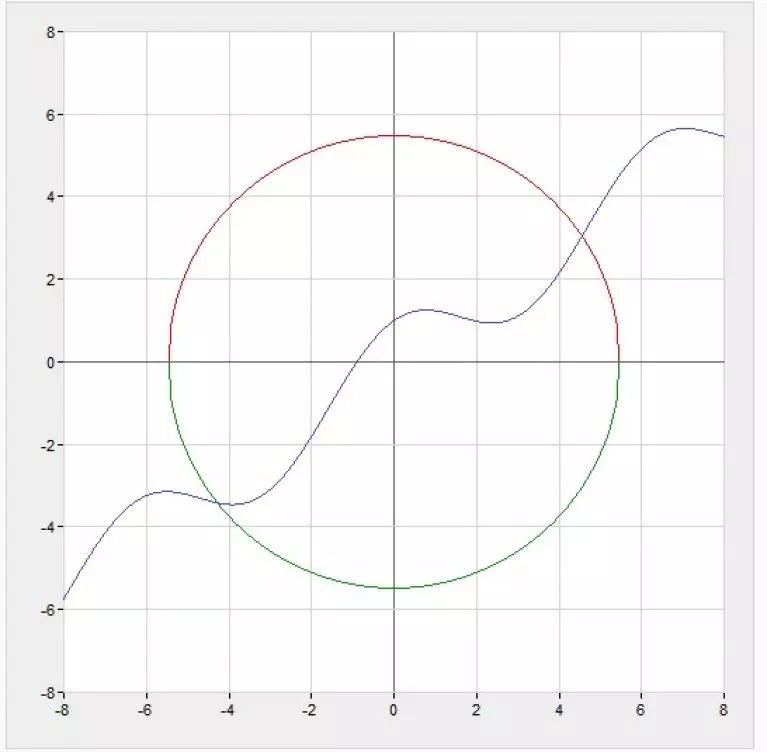 48.
48. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.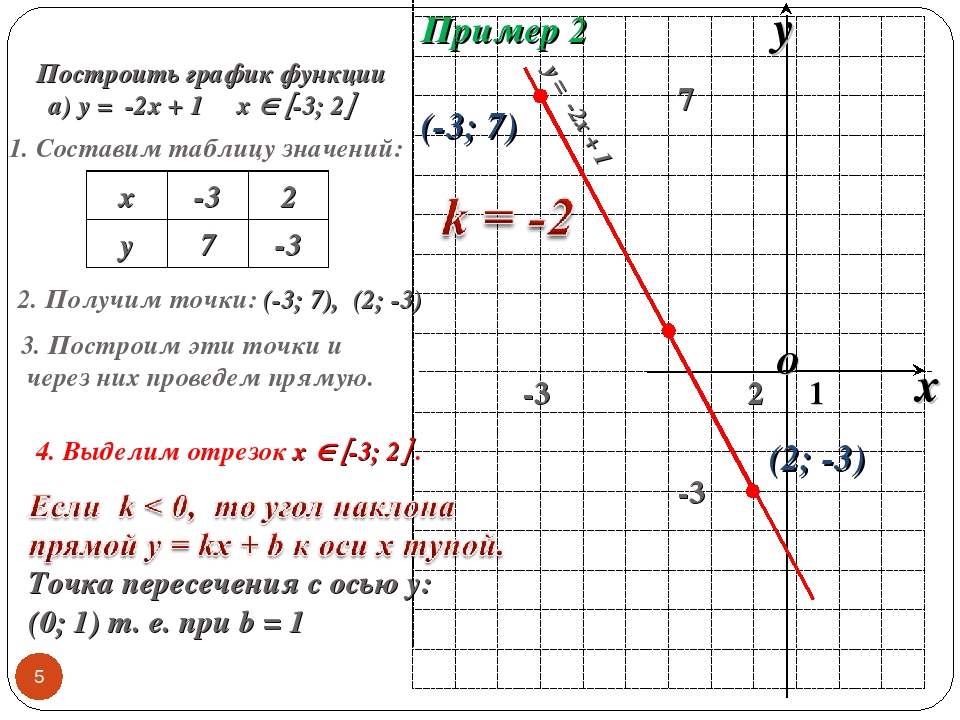
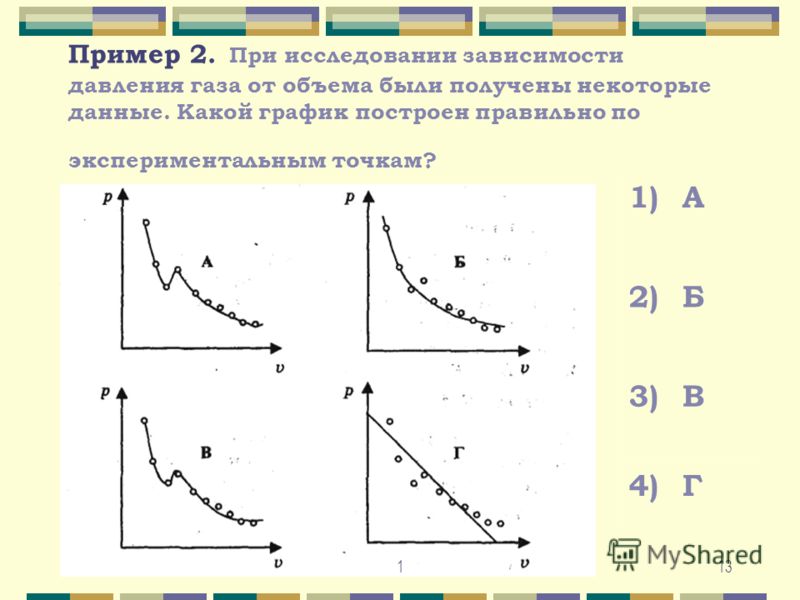
 При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) . Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций». На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента.
На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Здесь пример для y = 2 x (a = 2 > 1).
Здесь пример для y = 2 x (a = 2 > 1).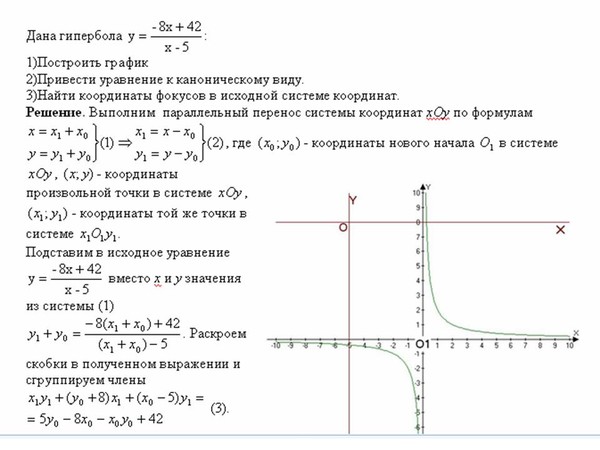 Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2
Графики функции существенно зависят от значения параметра a . Здесь пример для y = log 0,5 x (a = 1/2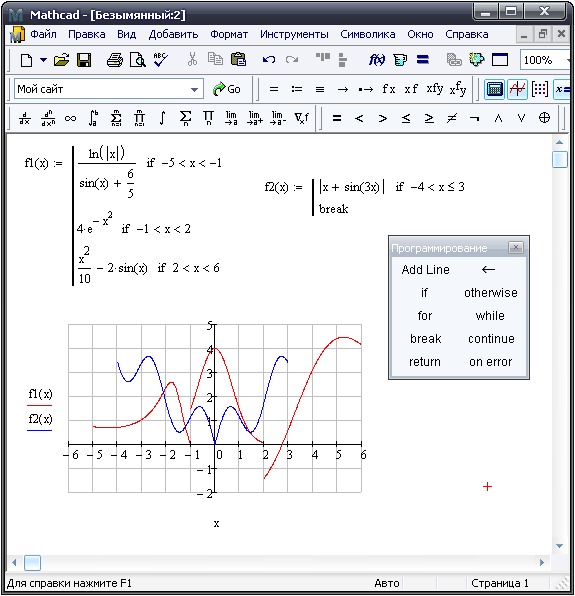
 Когда обе переменные являются количественными,
отрезок линии, соединяющий две точки на графике, выражает наклон,
которые можно визуально интерпретировать относительно наклона других линий
или выражается в виде точной математической формулы. Диаграммы разброса похожи
к линейным графикам, поскольку они начинаются с сопоставления точек количественных данных.
Разница в том, что с диаграммой рассеяния принимается решение, что
отдельные точки не должны напрямую соединяться
линия, но вместо этого выражает тенденцию.Эту тенденцию можно увидеть прямо через
распределение баллов или с добавлением линии регрессии.
Статистический инструмент, используемый для математического выражения тенденции в данных.
Когда обе переменные являются количественными,
отрезок линии, соединяющий две точки на графике, выражает наклон,
которые можно визуально интерпретировать относительно наклона других линий
или выражается в виде точной математической формулы. Диаграммы разброса похожи
к линейным графикам, поскольку они начинаются с сопоставления точек количественных данных.
Разница в том, что с диаграммой рассеяния принимается решение, что
отдельные точки не должны напрямую соединяться
линия, но вместо этого выражает тенденцию.Эту тенденцию можно увидеть прямо через
распределение баллов или с добавлением линии регрессии.
Статистический инструмент, используемый для математического выражения тенденции в данных.
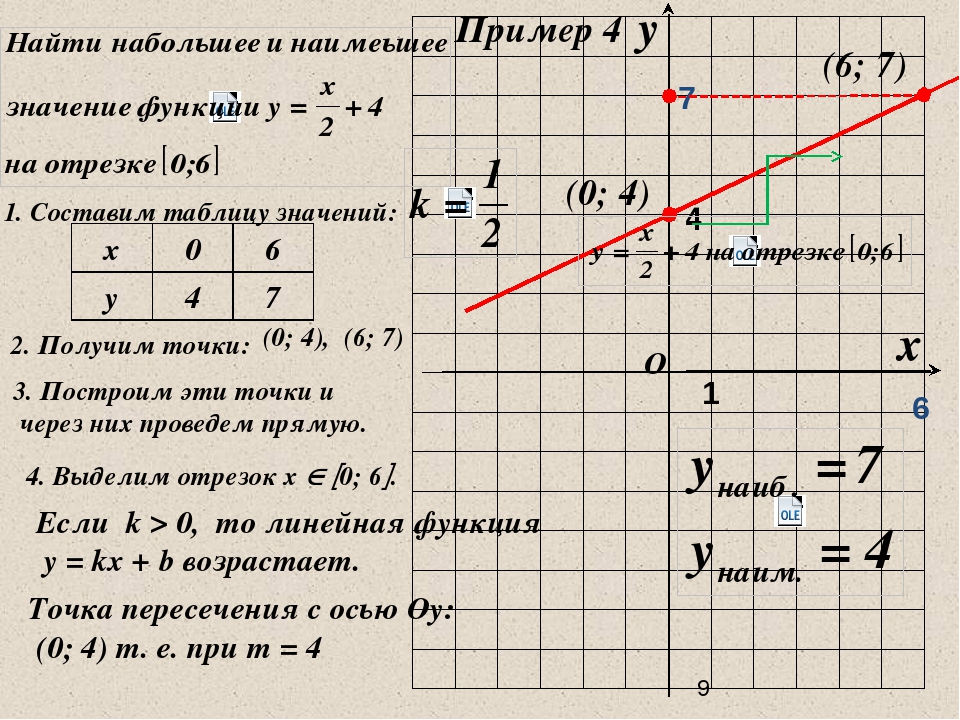
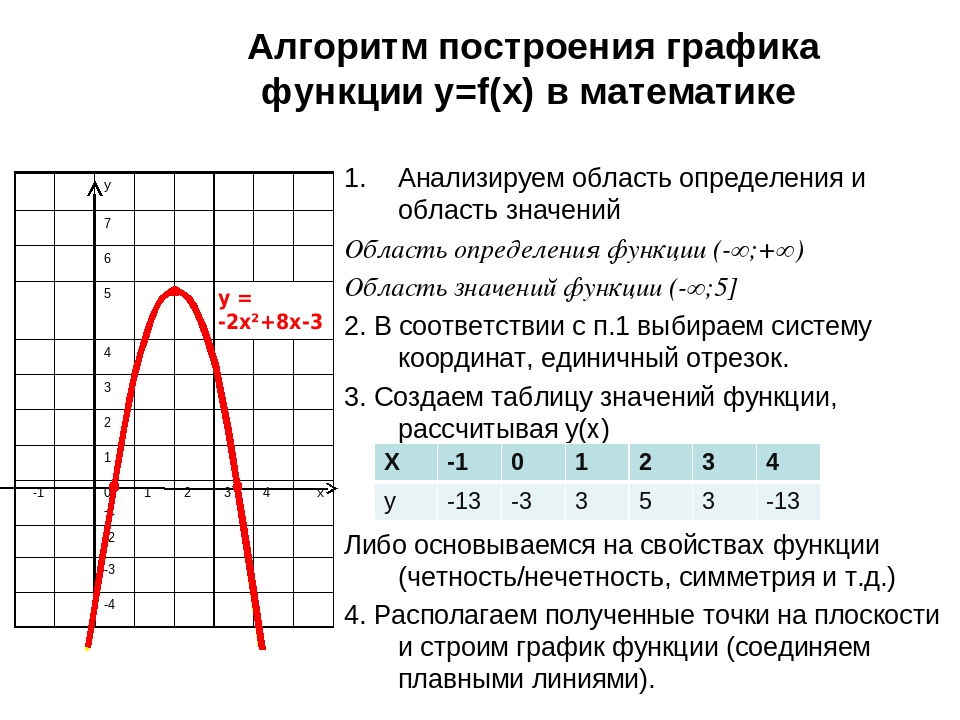


 {2} = 100 [/ латекс]
{2} = 100 [/ латекс]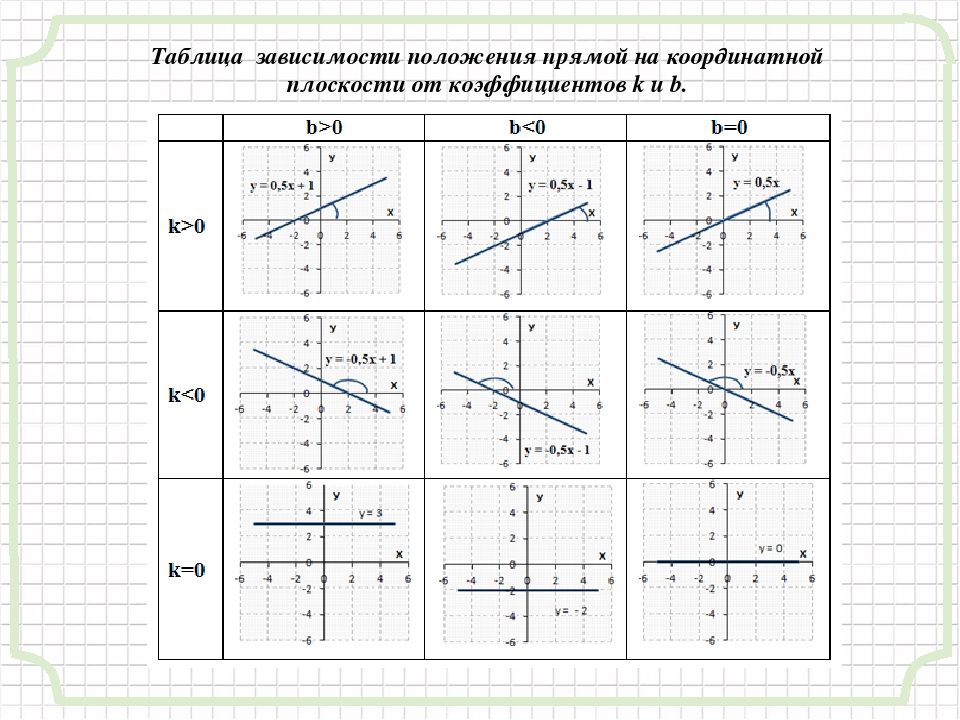


 3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является полиномом 3-й степени, называемым кубическим полиномом. .
3-9x [/ latex]: поскольку показатель [latex] x [/ latex] равен 3, это означает, что это уравнение является полиномом 3-й степени, называемым кубическим полиномом. .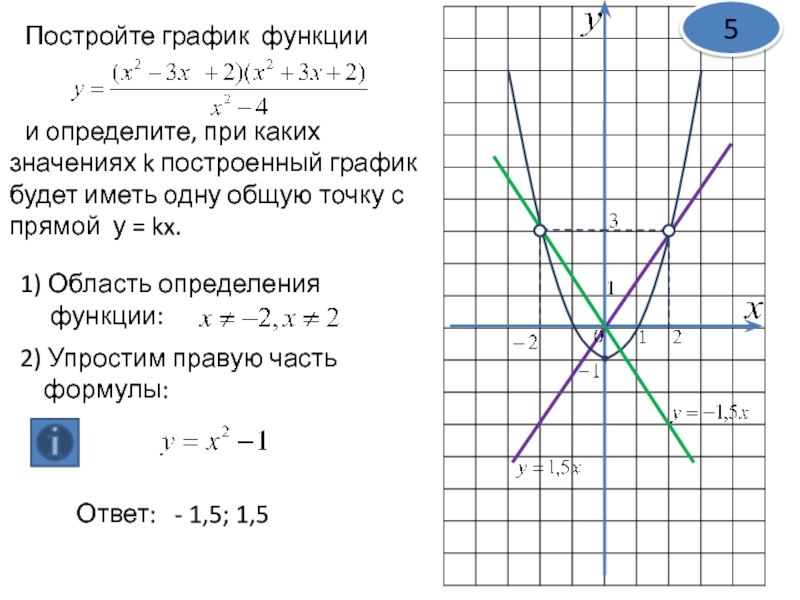


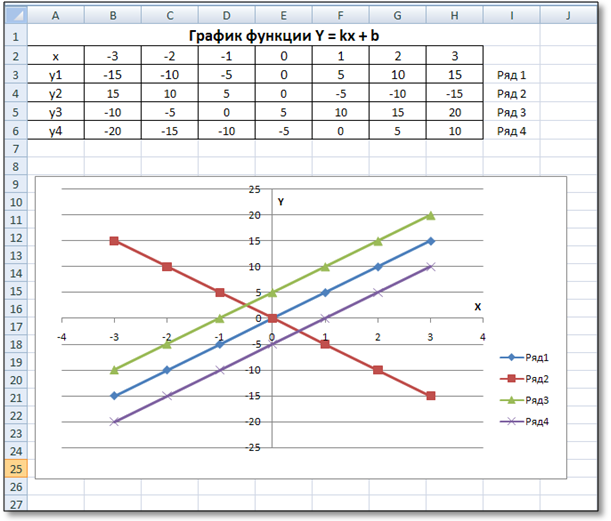 Это означает, что точки на линии являются решениями и являются частью графика.
Это означает, что точки на линии являются решениями и являются частью графика.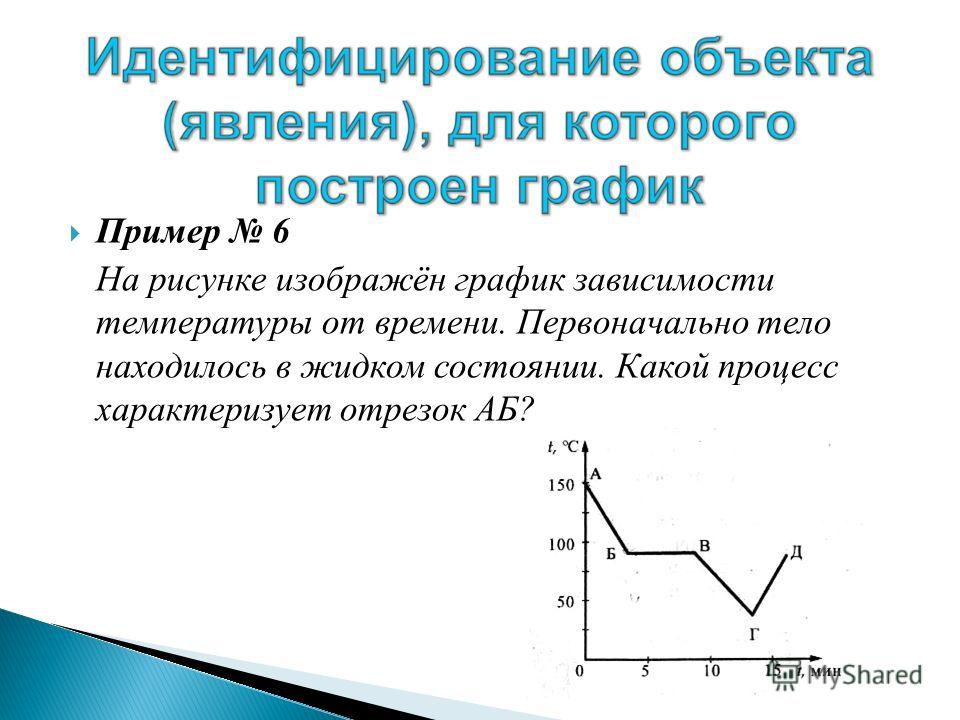 Полученная упорядоченная пара будет одним решением уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение:
Полученная упорядоченная пара будет одним решением уравнения. Итак, заменим [latex] x = 0 [/ latex], чтобы найти одно решение: Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим вместо [latex] (0, 0) [/ latex] в исходное неравенство:
Самая простая контрольная точка — [latex] (0, 0) [/ latex]. Подставим вместо [latex] (0, 0) [/ latex] в исходное неравенство:
 Это наиболее распространенный формат для построения научных данных, поскольку он отображает взаимосвязь между двумя переменными. Другие распространенные форматы графиков включают столбчатую диаграмму , показанную на рис.2 (и тесно связанный столбчатый график, в котором используются вертикальные, а не горизонтальные полосы) и круговая диаграмма , показанная на рис.3. Столбчатые и столбчатые диаграммы часто используются для отображения значений одной величины, измеренной для разных образцов, когда образцы различаются по типу, а не по количеству.
Это наиболее распространенный формат для построения научных данных, поскольку он отображает взаимосвязь между двумя переменными. Другие распространенные форматы графиков включают столбчатую диаграмму , показанную на рис.2 (и тесно связанный столбчатый график, в котором используются вертикальные, а не горизонтальные полосы) и круговая диаграмма , показанная на рис.3. Столбчатые и столбчатые диаграммы часто используются для отображения значений одной величины, измеренной для разных образцов, когда образцы различаются по типу, а не по количеству.
 Точка расположена на 21 единицу правее оси y (то есть на 21 единицу по оси x ) и 15 единиц.0 единиц над осью x (то есть 15,0 единиц по оси y ). Переменная, построенная по оси x , называется независимой переменной ; переменная, построенная по оси y , называется зависимой переменной . Перед нанесением данных на график часто бывает удобно перечислить данные в двух столбцах. Один содержит значения независимых переменных, обычно в числовом порядке; другой содержит соответствующие значения зависимых переменных.
Точка расположена на 21 единицу правее оси y (то есть на 21 единицу по оси x ) и 15 единиц.0 единиц над осью x (то есть 15,0 единиц по оси y ). Переменная, построенная по оси x , называется независимой переменной ; переменная, построенная по оси y , называется зависимой переменной . Перед нанесением данных на график часто бывает удобно перечислить данные в двух столбцах. Один содержит значения независимых переменных, обычно в числовом порядке; другой содержит соответствующие значения зависимых переменных.
Ваш комментарий будет первым