График y 2: постройте график функции y=2 — Школьные Знания.com

Графики функций. Простейшие построения. Прямая на плоскости

График функции — это наглядный образ некоторой функции f(x). Здесь каждому значению х соответствует единственное значение y. Это множество точек на плоскости, координаты которых удовлетворяют заданному уравнению y = f(x). График уравнения — это множество всех точек плоскости, которые удовлетворяют заданному уравнению, т.е. обращают уравнение в верное числовое равенство. Зависимость в данном случае не обязательно является функцией. Рассмотрим ряд элементарных функций, таких, как прямая, парабола, гипербола, их свойства и правила построения.

 

Но для начала покажем на примере отличие графика функции от графика уравнения.

График функции — для каждого значения Х единственное значение Y

График функции — для каждого значения Х единственное значение Y

График уравнения — для некоторого значения Х могут существовать несколько значений Y, не функция.

1. Прямая. Уравнение прямой y = kx + b.

Прямая задается линейной функцией , т.е. уравнением первой степени вида y = kx + b.

при k>0 график функции возрастает (y=3x+1, k=3, k>0), при k<0 график функции убывает (y=-3x+1, k=-3, k<0)

график функции возрастает k=3, k>0

график функции убывает k=-3, k<0

Рассмотрим частные случаи расположения линейных функций.

y = kx — график функции проходит через начало координат, т.е. точку О(0;0),

y = c (c = const) — график функции параллелен оси Ox,

x = c (c = const) — график функции параллелен оси Oy.

y = kx — график функции проходит через начало координат, т.е. точку О(0;0)

y = c (c = const) — график функции параллелен оси Ox

x = c (c = const) — график функции параллелен оси Oy

Для построения прямой достаточно получить координаты двух точек, принадлежащих заданному уравнению. 

Как построить прямую? Покажем на примере.

Дано уравнение прямой: y=-2x+3. Необходимо построить график функции.

Возьмем два произвольных значения переменной х, например х = -1 и х = 5. Найдем для каждого из них соответствующее значение переменной у. Как это сделать? Подставить выбранные значения х в заданное уравнение.

y(-1) = -2·(-1)+3=5

y(5) = -2·5+3=-7

Получаем две точки с координатами: (-1;5) и (5;-7). Выносим их на координатную плоскость и проводим через них прямую.

На что указывают параметры k,b в уравнении прямой y = kx + b?

Параметр k — указывает на наклон прямой.

Параметр b — координата точки пересечения заданной прямой с осью OY. Так как y = k·0 + b (х=0 — уравнение оси OY)

Наклон прямой в зависимости от k. k>0 — угол острый

Наклон прямой в зависимости от k. k<0 — угол тупой

Точки пересечения прямых с осью OY

Параметр k в уравнении прямой y = kx + b есть угловой коэффициент этой прямой.

k=tgα, α — угол меду положительным направлением оси ОХ и прямой.

Угловые коэффициенты всех параллельных прямых равны.

Угловые коэффициенты перпендикулярных прямых взаимно обратны по величине и противоположны по знаку.

Для наглядности покажем утверждения на конкретных примерах.

Угловой коэффициент прямой

Угловой коэффициент параллельных прямых

Угловой коэффициент перпендикулярных прямых

Уравнения прямой на плоскости.

Построим некоторые уравнения прямых в зависимости от исходных данных, приведем формулы и рассмотрим конкретные примеры.

Коротко уточним используемые ниже понятия:

Угол наклона прямой — угол меду положительным направлением оси ОХ и прямой.

Нормальный вектор прямой — вектор, перпендикулярный искомой прямой.

Направляющий вектор прямой — вектор, параллельный искомой прямой.

Уравнение прямой по заданной точке и углу наклона. Дано: A(x_A; y_A), α

Уравнение прямой по двум точкам

Уравнение прямой по точке и нормальному (направляющему) вектору/div>

2.

Парабола.

Парабола задается квадратичной функцией вида y = ax² + bx + c.

3. Гипербола.

4. Кубическая парабола.

 

График работы почты в Самарской области в майские праздники — 25 апреля 2023

Все новости

«Сейчас я нравлюсь себе больше»: красотки за 45 показали фото своих шикарных фигур — смотрим с восхищением

Под Самарой в ДТП насмерть разбились два человека

Жителям Самарской области запретили собирать ягоды и грибы

Где искать клеща — показываем на одной картинке

«Остальные — жалкое подобие». Сергей Зверев — о своем учителе Вячеславе Зайцеве, которого называли русским Карденом

Пицца против рыбных котлет. Какие продукты разрешены в школьных столовых — хитрый тест

Ипотека дороже, пенсия почтой, дети без вейпов: какие изменения ждут нас в мае 2023 года

Четыре человека погибли во время обстрела поселка в Брянской области. Новости СВО за 30 апреля

Умер известный советский и российский модельер Вячеслав Зайцев

Только для стройных: страны, в которых не рады людям с лишним весом (кое-где даже принудительно измеряют талию)

Кто сказал «мяу»? Отгадайте, из каких фильмов и сериалов эти 10 котиков

Мать в панике звала на помощь: история годовалой Василисы, которая умерла в больнице

Снесло полмашины: полиция озвучила версию смертельного ДТП на трассе в Самарской области

Май в Самарской области будет аномальным

Под Самарой сгорел пассажирский автобус

«Уехала, забрав все деньги из кассы»: парни рассказали о некрасивых поступках девушек при расставании

Пять минусов китайских автомобилей. Обобщаем опыт езды на «чайнакарах» 2023 года

В Сызрани мужчина подделал бомбу, чтобы напугать соседей

Стало известно, почему в Самарской области до сих пор не ввели тариф на похороны

Козероги будут ревновать, а Львы станут сексуальнее. Любовный гороскоп на май от астролога

«Я боюсь умереть каждый день». Певец Андрей Губин в день рождения откровенно рассказал о болезни, любви и возвращении на сцену

Ни пером описать. Как семья променяла спокойную пенсию на павлинью ферму

На зарубежные курорты или в Мин. Воды: куда из Самары можно улететь на майские праздники

«Алкаши пользуются тем, что скорая помощь бесплатная»: врачи рассказали, как им угрожали пациенты

В Самарской области ожидают жару до +31 градуса

Даже фрукты нельзя? Три полезные привычки, которые на самом деле убивают печень

«Запроса на «нового Кобзона» не было». Продюсеры и музыкальные критики — о феномене SHAMANа и секрете его популярности

В Самарской области простились с бойцом, погибшим в зоне СВО

Пригрели змею? 5 самых опасных женских знаков зодиака — среди них много стерв и разлучниц

Севастополь атаковали беспилотники, Украина готова к контрнаступлению. Новости СВО за 29 апреля

«Одной нет, вторая деформирована»: история пациентки, которая перенесла 10 операций после уменьшения груди в частной клинике

Надо, Федя, надо! Хорошо ли вы помните «Приключения Шурика»?

Питерский «Зенит» разгромил «Крылья Советов» на выезде

«Я никогда не была гадким утенком»: история нейрофизиолога, которая вышла на пенсию и стала моделью

«Могут и 10 кг съесть»: семья кормит на своем балконе диких коршунов — смотрите впечатляющие кадры

В Самарской области бизнесменам отдали 144 га под освоение. Рассказываем, что там хотят построить

Время моркови и свеклы: когда сажать популярные овощи и какие сорта выбрать

Села за руль в 75: как 80-летняя пенсионерка прокатила губернатора на самодельном авто по сгоревшей деревне

«Не могут отказаться»: зачем в Самарской области осужденных отправляют работать?

Все новости

Почтовые отделения 1 и 9 мая работать не будут

org/Person»>Фото: Евгений Вдовин / 161.RU

Поделиться

В майские праздники почтовые отделения Самарской области изменят график работы. 1 и 9 мая станут выходными днями для всех почтовых отделений в 63-м регионе.

8 мая почтовые отделения будут работать по графику воскресенья.

Со 2 по 7 мая почтовые отделения будут работать в обычном режиме.

— В выходные дни почтальоны не будут разносить письма и периодические печатные издания. Пенсии и пособия они доставят по графику, согласованному с региональным отделением Социального фонда РФ, — говорится в сообщении Почты России.

Самую оперативную информацию о жизни Самары и области мы публикуем в нашем телеграм-канале 63.RU. А в чат-боте вы можете предложить свои новости, истории, фотографии и видео. Также у нас есть группы во «ВКонтакте» и в «Одноклассниках». Читайте нас, где удобно.

По теме

• 27 декабря 2022, 11:18

  Опубликован график работы почты 31 декабря и в январские выходные

Марина Волгина

Почта РоссииГрафик работыПочта

• ЛАЙК0
• СМЕХ0
• УДИВЛЕНИЕ0
• ГНЕВ0
• ПЕЧАЛЬ0

Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter

КОММЕНТАРИИ0

Гость

Войти

Новости СМИ2

Новости СМИ2

Графики и решения систем линейных уравнений

Результаты обучения

• Графические системы уравнений
  • График системы двух линейных уравнений
  • Нарисуйте график системы двух линейных неравенств
• Оцените упорядоченные пары как решения для систем
  • Определить, является ли упорядоченная пара решением системы линейных уравнений
  • Определить, является ли упорядоченная пара решением системы линейных неравенств
• Классифицировать решения для систем
  • Определить тип решения системы на основе ее графа

 

То, как течет река, зависит от многих переменных, в том числе от того, насколько велика река, сколько в ней воды, какие предметы плавают в реке, идет ли дождь и так далее. Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.

Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений в каждом приложении математики. Они являются полезным инструментом для обнаружения и описания того, как поведение или процессы взаимосвязаны. Например, редко можно найти модель транспортного потока, на которую влияет только погода. Аварии, время суток и крупные спортивные мероприятия — это лишь некоторые из других переменных, которые могут повлиять на транспортный поток в городе. В этом разделе мы рассмотрим некоторые основные принципы построения графика и описания пересечения двух линий, составляющих систему уравнений.

Нарисуйте график системы линейных уравнений

В этом разделе мы рассмотрим системы линейных уравнений и неравенства с двумя переменными.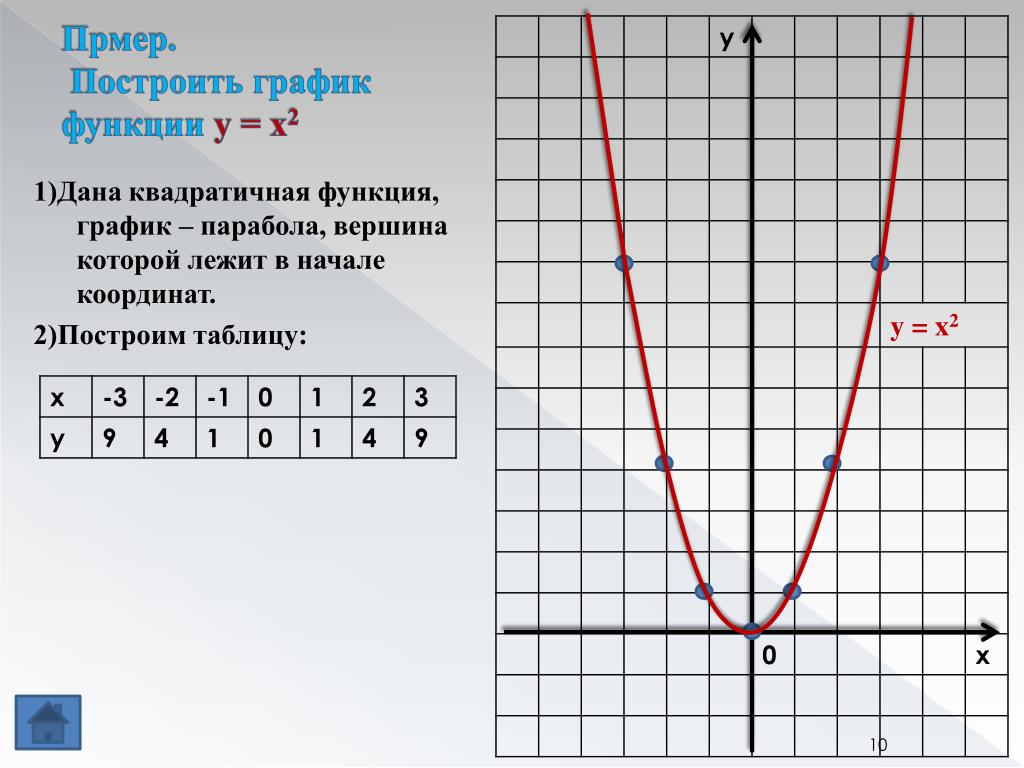 Сначала мы попрактикуемся в построении графиков двух уравнений на одной и той же системе осей, а затем рассмотрим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одной и той же системе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения отдельных линейных уравнений. Мы можем использовать таблицы значений, наклона и y — точка пересечения, или x — и y — точки пересечения для построения обеих линий на одном наборе осей.

Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс]\begin{array}{r}2x+y=-8\\ x-y=-1\end{array}[/latex]

Давайте нарисуем их, используя форму пересечения наклона на том же наборе осей. . Помните, что форма пересечения наклона выглядит как [latex]y=mx+b[/latex], поэтому нам нужно решить оба уравнения для [latex]y[/latex].

Сначала найдите y в [латекс]2x+y=-8[/латекс]

[латекс]\begin{array}{c}2x+y=-8\\ y=-2x — 8\end {array}[/latex]

Во-вторых, найдите y в [latex]x-y=-1[/latex]

[latex]\begin{array}{r}x-y=-1\,\,\,\ ,\,\\ y=x+1\end{array}[/latex]

Теперь система записывается как

[latex]\begin{array}{c}y=-2x — 8\\y= x+1\end{array}[/latex]

Теперь вы можете построить графики обоих уравнений, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже. Обратите внимание, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы проверим, что эта точка является решением системы.

 В следующем примере вам будет предложена система для построения графика, состоящего из двух параллельных линий.

Пример

Постройте график системы [латекс]\begin{array}{c}y=2x+1\\y=2x-3\end{массив}[/latex], используя наклоны и точки пересечения y линий .

Показать раствор

В следующем примере вам будет дана система, уравнения которой выглядят по-разному, но после построения графика оказываются одной и той же линией.

Пример

Постройте график системы [latex]\begin{array}{c}y=\frac{1}{2}x+2\\2y-x=4\end{array}[/latex], используя x — и y-перехваты.

Показать раствор

Построение графика системы линейных уравнений состоит из выбора метода построения графика, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей.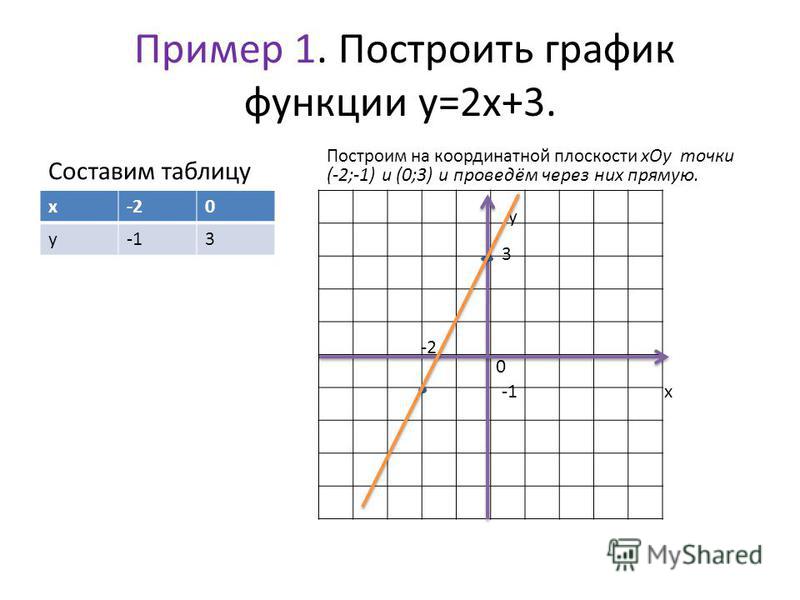

Когда вы рисуете систему линейных неравенств на одном и том же наборе осей, вам нужно учитывать еще несколько моментов.

Нарисуйте график системы двух неравенств

Помните из модуля по построению графиков, что график одного линейного неравенства расщепляет координатную плоскость на две области. На одной стороне лежат все решения неравенства. С другой стороны решений нет. Рассмотрим график неравенства [latex]y<2x+5[/latex].

Пунктирная линия: [латекс]у=2х+5[/латекс]. Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство x и y координаты точек A и B — вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.

Линия границы делит координатную плоскость пополам. В данном случае она показана пунктирной линией, так как точки на прямой не удовлетворяют неравенству. Если бы неравенство было [латекс]y\leq2x+5[/латекс], то граница была бы сплошной.

Нарисуем другое неравенство: [латекс]у>-х[/латекс]. Вы можете проверить пару точек, чтобы определить, какую сторону линии границы следует заштриховать. Проверка точек M и N дает верные утверждения. Итак, заштриховываем область над линией. Линия пунктирная, так как точки на прямой не соответствуют действительности.

Чтобы создать систему неравенств, вам нужно построить график двух или более неравенств. Давайте использовать [латекс]y<2x+5[/латекс] и [латекс]у>-х[/латекс], так как мы уже построили график каждого из них.

Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [латекс]у>-х[/латекс], так и для [латекс]у<2x+5[/латекс].

В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.

Примеры

График системы [латекс]\начало{массив}{с}у\ге2х+1\\у\lt2x-3\конец{массив}[/латекс]

Показать решение

В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.

Определите, является ли упорядоченная пара решением системы линейных уравнений

Линии на приведенном выше графике определены как

[латекс]\начало{массив}{r}2x+y=-8\\ x-y=-1\конец{массив}[/латекс].

Они пересекаются в месте, похожем на [латекс]\влево(-3,-2\вправо)[/латекс].

Используя алгебру, мы можем проверить, что эта общая точка на самом деле [латекс]\влево(-3,-2\вправо)[/латекс], а не [латекс]\влево(-2,999,-1,999\вправо)[/ латекс]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка дает верное утверждение, значит, вы нашли решение системы уравнений!

Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении. В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.

Подумай об этом

Является ли [латекс](−2,4)[/латекс] решением для системы

[латекс]\begin{array}{r}y=2x\\3x+2y=1\ end{array}[/latex]

Прежде чем делать какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?

Показать раствор

Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.

Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.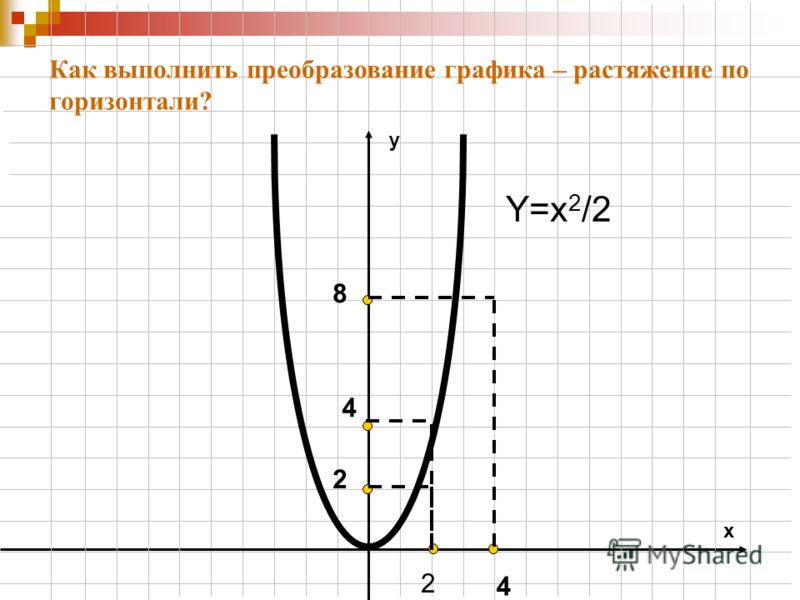

Определить, является ли упорядоченная пара решением системы линейных неравенств

На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, поскольку их координаты делают оба утверждения неравенства верными.

Напротив, точки M и A лежат вне области решения (фиолетовый). Хотя точка M является решением неравенства [латекс]y>−x[/латекс], а точка А является решением неравенства [латекс]у<2x+5[/латекс], ни одна из точек не является решением система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.

Вот график системы в приведенном выше примере. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия двух неравенств.

Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).

Как показано выше, найти решения системы неравенств можно путем построения графика каждого неравенства и определения области, которую они разделяют. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графе для системы двух линейных неравенств. Общие шаги описаны ниже:

• Изобразите каждое неравенство в виде линии и определите, будет ли она сплошной или пунктирной
• Определите, какая сторона каждой граничной линии представляет решения неравенства, проверив точку на каждой стороне
• Закрасьте область, представляющую решения для обоих неравенств

В этом разделе мы видели, что решения систем линейных уравнений и неравенств могут быть упорядочены попарно. В следующем разделе мы будем работать с системами, которые не имеют решений или имеют бесконечно много решений.

Используйте график для классификации решений систем.

Вспомните, что график линейного уравнения представляет собой линию, которая указывает на то, что все точки на линии являются решениями этого линейного уравнения. Существует бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, которые пересекаются в одной точке, эта точка является решением системы. Что произойдет, если прямые никогда не пересекутся, как в случае с параллельными прямыми? Как бы вы описали решения для такой системы? В этом разделе мы рассмотрим три возможных результата решения системы линейных уравнений.

Три возможных результата для решений систем уравнений

Напомним, что решением системы уравнений является значение или значения, которые верны для всех уравнений в системе. Есть три возможных результата для решений систем линейных уравнений. Графики уравнений в системе могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждом изображены две линии, составляющие систему уравнений.

Одно решение	Нет решений	Бесконечные решения
Если графики уравнений пересекаются, то существует одно решение, верное для обоих уравнений.	Если графики уравнений не пересекаются (например, если они параллельны), то нет решений, верных для обоих уравнений.	Если графики уравнений одинаковы, то существует бесконечное число решений, верных для обоих уравнений.

• Одно решение:  Когда система уравнений пересекается по упорядоченной паре, система имеет одно решение.
• Бесконечное количество решений: Иногда два уравнения представляют собой одну линию, и в этом случае у нас есть бесконечное количество решений.
• Нет решения: Когда линии, составляющие систему, параллельны, решений нет, потому что две линии не имеют общих точек.