X5 Retail Group (FIVE) — дивиденды компании, график стоимости акций. Прогноз цены X5 Retail Group (FIVE) :: РБК Инвестиции
Дивиденды
Выводим дату закрытия реестра акционеров. Чтобы успеть получить дивиденды по акции, необходимо успеть купить её не менее чем за 2 торговых дня до указанной даты
18 декабря 2020 73,65 2,69% 29 мая 2020 110,47 5,29% 24 мая 2019 90,06 4,93% 25 мая 2018 79,5 4,31%
Функция y x3 (х в кубе), график функции, урок и презентация
Дата публикации: . 3+ 1$.
3+ 1$.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
- функция, аргумент функции, значение функции
- график функции, преобразование графика функции
- свойства функции, исследование свойств функции
Глоссарий по теме урока
Определение
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
у — зависимая переменная, значение функции
Определение
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Определение
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
- для любого х из области определения выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Определение
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2.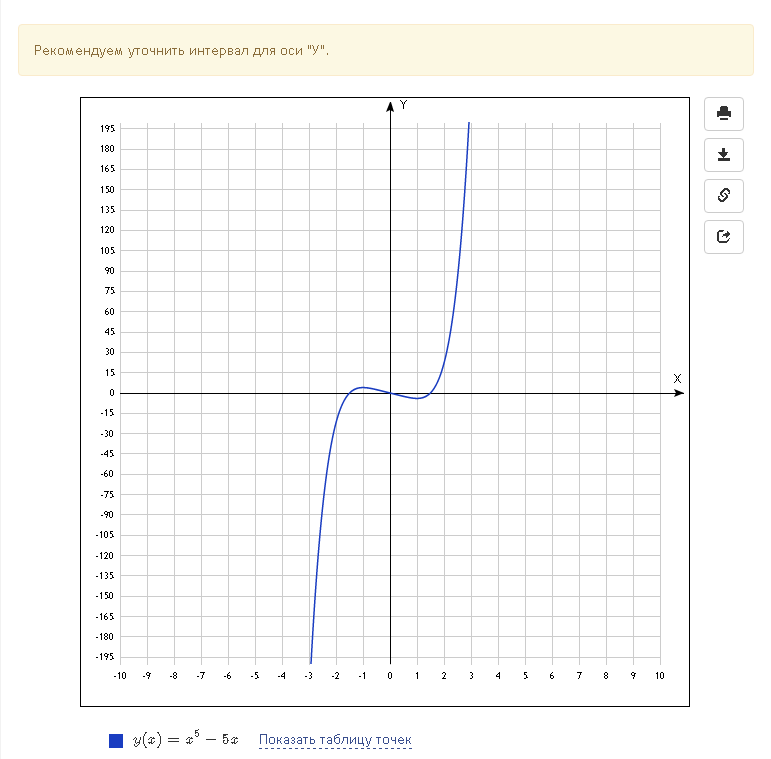
Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких что, х1<х2, выполняется неравенство у1>у2.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Дополнительная литература:
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
https://mathb-ege.sdamgia.ru/test?theme=177
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
- Множество значений функции
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
- Четность / нечетность функции
D(y)= — симметрична относительно нуля
,
следовательно, функция четная и ее график симметричен относительно оси ОУ
- Нули функции
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
- Промежутки знакопостоянства
у>0 при
у<0 при
- Монотонность
Найдем производную
Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.
Определим знаки производной в полученных промежутках.
точки -1, 1 – выколоты, 0 — закрашена
Производная положительна, а значит, функция возрастает при .
Производная отрицательна, а значит, функция убывает при
- Экстремум
х=0 – стационарная точка.
В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.
Значение функции в точке максимума
- Дополнительные точки
у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4
- Отразим найденные свойства графически, построим график функции
2. Решение задачи на оптимизацию
Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.
В решении таких задач выделяют 3 основных этапа:
1 этап. «Перевод» задачи на язык функций:
- вводят независимую переменную х
- выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
- выражают у через х и другие известные величины
- устанавливают по условию задачи границы изменения переменной х
2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.
Рассмотрим план решения на примере задачи.
Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
Решение:
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x2 у. е.
е.
Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)2 (у.е.)
Всем рабочим нужно заплатить 4x2+(24 — x)2 = 5x2 -48x+576 (у.е.)
Причем 0≤ x ≤ 24, x ϵ N.
2 этап.
Рассмотрим функцию f(x)=5x2-48x+576.
Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x0 = 4,8 .
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
Функции |
у=0 |
у=sin(x+5π/2) |
у=lg(x+10) |
Решение:
- у=0
область определения – множество действительных чисел – симметрична относительно нуля
у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.
Данная функция одновременно четна и нечетна.
- у=sin(x+5π/2)
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
- у=lg(x+10)
логарифмируемое выражение должно быть положительным
x+10>0; x>-10
D(y): x>-10
Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.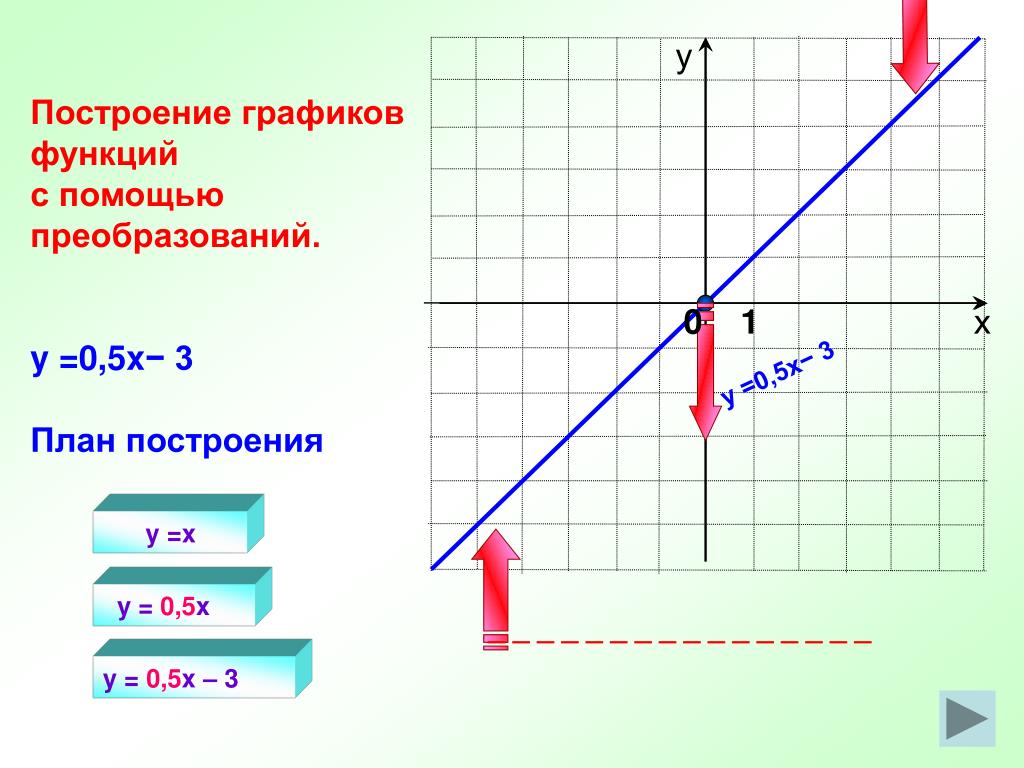
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
Зайдем с другого конца, выразим -f(x):
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
Ответ:
Функции | Четность / нечетность |
у=0 | и четная, и нечетная |
у=sin(x+5π/2) | четная |
у=lg(x+10) | общего вида |
нечетная |
2.
Решение:
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7
Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:
Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.
Выполним построения выделенных функций.
Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.
Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.
Ответ:
Акции X5 Retail Group US98387E2054, FIVE, PJP график, цена акции, архив котировок
AMEX
Armenia Securities Exchange
Astana International Exchange
B3 S. A. — Brasil, Bolsa, Balcao
A. — Brasil, Bolsa, Balcao
BCBA (расчеты осуществляются в Аргентине в ARS)
BSE
Euronext Amsterdam
Euronext Brussels
Euronext Lisbon
Euronext London
Euronext Oslo
Euronext Paris
Iran Fara Bourse
KASE
Latibex (Испания)
MAB (Alternative Equity Market, Испания)
Muscat Securities Market
NASDAQ
NASDAQ OMX Copenhagen
NASDAQ OMX Helsinki
NASDAQ OMX Iceland
NASDAQ OMX Stockholm
NYSE
Nasdaq Nordic
Nasdaq OMX Балтия
RTS Board
SIBE (Испания)
Taipei Exchange (Trading System)
Австралийская ФБ
Амманская ФБ
Афинская Ф. Б.
Б.
БВФБ
Бакинская ФБ
Бахрейнская ФБ
Бейрутская ФБ
Берлинская биржа
Болгарская ФБ
Братиславская ФБ
Будапештская ФБ
Бухарестская ФБ
Варшавская ФБ
Венская ФБ
Гамбургская ФБ
Ганноверская ФБ
Гонконгская ФБ
Грузинская ФБ
Даккийская ФБ
Дубайский финансовый рынок
Дюссельдорфская ФБ
Загребская ФБ
Индонезийская ФБ
Ирландская ФБ
Итальянская ФБ
Йоханнесбургская ФБ
Катарская ФБ
Корейская ФБ
Кувейтская ФБ
Кыргызская ФБ
Лондонская ФБ
Люблянская ФБ
Люксембургская ФБ
Малайзийская биржа
Мальтийская ФБ
Московская Биржа
Московская Биржа. Внебиржевые сделки
Внебиржевые сделки
Московская биржа. Вечерняя сессия
Мюнхенская ФБ
Намибийская фондовая биржа
Национальная фондовая биржа Индии
Новозеландская ФБ
ПФТС
Палестинская ФБ
Пражская ФБ
Санкт-Петербургская биржа
Саудовская ФБ
Сингапурская ФБ
Стамбульская ФБ
Тайваньская ФБ
Тель-Авивская ФБ
Токийская ФБ
Укрбиржа
ФБ Абу-Даби
ФБ Коломбо
ФБ Молдовы
ФБ Сантьяго
ФБ Таиланда
ФБ Торонто
ФБ Тошкент
ФБ Хошимина
Филиппинская ФБ
Фондовая Биржа Кипра
Франкфуртская ФБ
Ханойская ФБ (Вьетнам)
Читтагонгская ФБ
Шанхайская ФБ
Швейцарская ФБ
Штутгартская ФБ
Шэньчжэньская ФБ
Глава 6 Продвинутая графика | Визуализация и анализ географических данных на языке R
Предварительные требования
Для работы по теме текущей лекции вам понадобятся пакеты ggplot2, dplyr и tidyr из tidyverse. Помимо этого, мы будем работать напрямую с данными Евростата, NASA POWER и USDA NRCS Soil Data Access к которым можно обращаться напрямую с использованием пакетов
Помимо этого, мы будем работать напрямую с данными Евростата, NASA POWER и USDA NRCS Soil Data Access к которым можно обращаться напрямую с использованием пакетов eurostat, nasapower и soildb:
Пакет soilDB лучше устанавливать из консоли командой
install.packages('soilDB', dependencies = TRUE). Указание параметраdependencies = TRUEобеспечит установку других пакетов, от которых он зависит.
В настоящей главе мы кратко познакомимся с системой ggplot2. gg расшифровывается как grammar of graphics. Под этим понимается определенная (какая — мы узнаем далее) система правил, позволяющих описывать и строить графики. ggplot довольно сильно отличается от стандартной графической подсистемы R. Прежде всего — модульным подходом к построению изображений. В ggplot вы собираете графики «по кирпичикам», отдельно определяя источник данных, способы изображения, параметры системы координат и т. д. – путем вызова и сложения результатов соответствующих функций.
д. – путем вызова и сложения результатов соответствующих функций.
При построении элементарных графиков ggplot может показаться (и по факту так и есть) сложнее, чем стандартная графическая подсистема. Однако при усложнении требований к внешнему виду и информационному насыщению графика сложность ggplot оказывается преимуществом, и с ее помощью относительно просто можно получать элегантные и информативные визуализации, на создание которых с помощью стандартной подсистемы пришлось бы затратить невероятные усилия! В этой главе мы кратко познакомимся с ggplot, а далее на протяжении курса будем регулярно ее использовать, осваивая новые возможности.
Загрузка данных Евростата
Таблицы данных Евростата имеют уникальные коды, по которым их можно загружать, используя API (Application programming interface). В этой лекции мы будем работать с данными о крупнейших международных партнерах Евросоюза по импорту и экспорту основных видов товаров. Например, таблица данных по продуктам питания, напиткам и табаку имеет код tet00034:
Например, таблица данных по продуктам питания, напиткам и табаку имеет код tet00034:
Для чтения таблиц по кодам в пакете eurostat имеется функция get_eurostat(). Чтобы год измерения получить в виде числа, а не объекта типа Date, используем второй параметр time_format = num. Для перехода от кодов продукции и стран к их полным наименованиям, дополнительно вызовем функцию label_eurostat() из того же пакета:
tables = c('tet00034', 'tet00033', 'tet00032', 'tet00031','tet00030', 'tet00029')
trades = lapply(tables, function(X) { # прочтем несколько таблиц в список
get_eurostat(X) %>% label_eurostat()
}) %>%
bind_rows() %>% # объединим прочитанные таблицы в одну
select(-geo) %>% # убираем столбец с территорией торговли, т.к. там только Евросоюз
dplyr::filter(stringr::str_detect(indic_et, 'Exports in|Imports in')) %>% # оставим только экспорт и импорт
pivot_wider(names_from = indic_et, values_from = values) %>% # вынесем данные по экспорту и импорту в отдельные переменные
rename(export = `Exports in million of ECU/EURO`, # дадим им краткие названия
import = `Imports in million of ECU/EURO`) %>%
mutate(partner = as. factor(partner))
trades # посмотрим, что получилось
## # A tibble: 720 x 5
## sitc06 partner time export import
## <chr> <fct> <date> <dbl> <dbl>
## 1 Food, drinks and tobacco Argentina 2008-01-01 81.3 7334
## 2 Food, drinks and tobacco Brazil 2008-01-01 600. 9639.
## 3 Food, drinks and tobacco Canada 2008-01-01 1950. 1458.
## 4 Food, drinks and tobacco Switzerland 2008-01-01 5000. 2727.
## 5 Food, drinks and tobacco China except Hong Kong 2008-01-01 1322. 3567.
## 6 Food, drinks and tobacco Japan 2008-01-01 3964. 119.
## 7 Food, drinks and tobacco Norway 2008-01-01 2416. 3012.
## 8 Food, drinks and tobacco Russia 2008-01-01 7567. 855.
## 9 Food, drinks and tobacco Turkey 2008-01-01 1175 3160.
## 10 Food, drinks and tobacco United States 2008-01-01 10021.
factor(partner))
trades # посмотрим, что получилось
## # A tibble: 720 x 5
## sitc06 partner time export import
## <chr> <fct> <date> <dbl> <dbl>
## 1 Food, drinks and tobacco Argentina 2008-01-01 81.3 7334
## 2 Food, drinks and tobacco Brazil 2008-01-01 600. 9639.
## 3 Food, drinks and tobacco Canada 2008-01-01 1950. 1458.
## 4 Food, drinks and tobacco Switzerland 2008-01-01 5000. 2727.
## 5 Food, drinks and tobacco China except Hong Kong 2008-01-01 1322. 3567.
## 6 Food, drinks and tobacco Japan 2008-01-01 3964. 119.
## 7 Food, drinks and tobacco Norway 2008-01-01 2416. 3012.
## 8 Food, drinks and tobacco Russia 2008-01-01 7567. 855.
## 9 Food, drinks and tobacco Turkey 2008-01-01 1175 3160.
## 10 Food, drinks and tobacco United States 2008-01-01 10021. \circ\) Выгрузим данные по температуре, относительной влажности и осадкам в Екатеринбурге (\(60.59~в.д.\), \(56.84~с.ш.\)) за период с 1 по 30 апреля 1995 года:
\circ\) Выгрузим данные по температуре, относительной влажности и осадкам в Екатеринбурге (\(60.59~в.д.\), \(56.84~с.ш.\)) за период с 1 по 30 апреля 1995 года:
daily_single_ag <- get_power(
community = "AG",
lonlat = c(60.59, 56.84),
pars = c("Rh3M", "T2M", "PRECTOT"),
dates = c("1995-04-01", "1995-04-30"),
temporal_average = "DAILY"
)
daily_single_ag # посмотрим, что получилось
## NASA/POWER SRB/FLASHFlux/MERRA2/GEOS 5.12.4 (FP-IT) 0.5 x 0.5 Degree Daily Averaged Data
## Dates (month/day/year): 04/01/1995 through 04/30/1995
## Location: Latitude 56.84 Longitude 60.59
## Elevation from MERRA-2: Average for 1/2x1/2 degree lat/lon region = 279.98 meters Site = na
## Climate zone: na (reference Briggs et al: http://www.energycodes.gov)
## Value for missing model data cannot be computed or out of model availability range: NA
##
## Parameters:
## PRECTOT MERRA2 1/2x1/2 Precipitation (mm day-1) ;
## T2M MERRA2 1/2x1/2 Temperature at 2 Meters (C) ;
## Rh3M MERRA2 1/2x1/2 Relative Humidity at 2 Meters (%)
##
## # A tibble: 30 x 10
## LON LAT YEAR MM DD DOY YYYYMMDD Rh3M T2M PRECTOT
## <dbl> <dbl> <dbl> <int> <int> <int> <date> <dbl> <dbl> <dbl>
## 1 60. 2/day)
##
## # A tibble: 4 x 17
## LON LAT PARAMETER YEAR JAN FEB MAR APR MAY JUN JUL AUG
## <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 60.6 56.8 CLRSKY_S… 1995 0.91 2.07 3.93 5.93 7.27 7.98 7.54 6.13
## 2 60.6 56.8 CLRSKY_S… 1996 0.94 2.12 4.02 6.24 7.37 7.93 7.42 6.23
## 3 60.6 56.8 ALLSKY_S… 1995 0.68 1.41 2.8 4.75 5.42 6.04 5.78 4.13
## 4 60.6 56.8 ALLSKY_S… 1996 0.76 1.57 3.39 4.82 5.3 6.2 5.58 4.5
## # … with 5 more variables: SEP <dbl>, OCT <dbl>, NOV <dbl>, DEC <dbl>,
## # ANN <dbl>
2/day)
##
## # A tibble: 4 x 17
## LON LAT PARAMETER YEAR JAN FEB MAR APR MAY JUN JUL AUG
## <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 60.6 56.8 CLRSKY_S… 1995 0.91 2.07 3.93 5.93 7.27 7.98 7.54 6.13
## 2 60.6 56.8 CLRSKY_S… 1996 0.94 2.12 4.02 6.24 7.37 7.93 7.42 6.23
## 3 60.6 56.8 ALLSKY_S… 1995 0.68 1.41 2.8 4.75 5.42 6.04 5.78 4.13
## 4 60.6 56.8 ALLSKY_S… 1996 0.76 1.57 3.39 4.82 5.3 6.2 5.58 4.5
## # … with 5 more variables: SEP <dbl>, OCT <dbl>, NOV <dbl>, DEC <dbl>,
## # ANN <dbl>
Загрузка данных Soil Data Access
Soil Data Access — это онлайн-сервис департамента сельского хозяйства США, который позволяет получать подробные данные о почвенных ресурсах этой страны. Наиболее часто запрашиваются данные по так называемым почвенным сериям — группам почвенных профилей, обладающих схожими характеристиками и, таким образом, идентичными с точки зрения сельскохозяйственного использования. Как правило, серии именуются по названию населенного пункта, рядом с которым впервые были найдены подобные почвы.
Как правило, серии именуются по названию населенного пункта, рядом с которым впервые были найдены подобные почвы.
Например, серия Cecil имеет следующее покрытие и обеспеченность разрезами в базе данных SDA при запросе на сайте Series Extent Explorer:
Для запросов данных по почвенным сериям достаточно вызвать функцию fetchOSD и передать ей имя одной или более серий:
soils = c('wilkes', 'chewacla', 'congaree')
series = fetchOSD(soils, extended = TRUE)
Результирющий объект представляет собой список со множеством таблиц, которые характеризуют как почвенную серию в целом, так и отдельные ее разрезы:
str(series)
## List of 13
## $ SPC :Formal class 'SoilProfileCollection' [package "aqp"] with 9 slots
## .. ..@ idcol : chr "id"
## .. ..@ hzidcol : chr "hzID"
## .. ..@ depthcols : chr [1:2] "top" "bottom"
## .. ..@ metadata :List of 8
## .. .. ..$ aqp_df_class : chr "data. frame"
## .. .. ..$ aqp_group_by : chr ""
## .. .. ..$ aqp_hzdesgn : chr "hzname"
## .. .. ..$ aqp_hztexcl : chr "texture_class"
## .. .. ..$ depth_units : chr "cm"
## .. .. ..$ stringsAsFactors: logi FALSE
## .. .. ..$ original.order : int [1:22] 1 2 3 4 5 6 7 8 9 10 ...
## .. .. ..$ origin : chr "OSD via Soilweb / fetchOSD"
## .. ..@ horizons :'data.frame': 22 obs. of 19 variables:
## .. .. ..$ id : chr [1:22] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## .. .. ..$ top : int [1:22] 0 10 36 66 97 119 152 0 20 46 ...
## .. .. ..$ bottom : int [1:22] 10 36 66 97 119 152 203 20 46 56 ...
## .. .. ..$ hzname : chr [1:22] "Ap" "Bw1" "Bw2" "Bw3" ...
## .. .. ..$ soil_color : chr [1:22] "#7E5A3BFF" "#7A5C37FF" "#7A5C37FF" "#7E5A3BFF" ...
## .. .. ..$ hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ value : int [1:22] 4 4 4 4 5 5 4 4 4 3 ...
## .. .. ..$ chroma : int [1:22] 4 4 4 4 8 1 4 4 3 3 .
frame"
## .. .. ..$ aqp_group_by : chr ""
## .. .. ..$ aqp_hzdesgn : chr "hzname"
## .. .. ..$ aqp_hztexcl : chr "texture_class"
## .. .. ..$ depth_units : chr "cm"
## .. .. ..$ stringsAsFactors: logi FALSE
## .. .. ..$ original.order : int [1:22] 1 2 3 4 5 6 7 8 9 10 ...
## .. .. ..$ origin : chr "OSD via Soilweb / fetchOSD"
## .. ..@ horizons :'data.frame': 22 obs. of 19 variables:
## .. .. ..$ id : chr [1:22] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## .. .. ..$ top : int [1:22] 0 10 36 66 97 119 152 0 20 46 ...
## .. .. ..$ bottom : int [1:22] 10 36 66 97 119 152 203 20 46 56 ...
## .. .. ..$ hzname : chr [1:22] "Ap" "Bw1" "Bw2" "Bw3" ...
## .. .. ..$ soil_color : chr [1:22] "#7E5A3BFF" "#7A5C37FF" "#7A5C37FF" "#7E5A3BFF" ...
## .. .. ..$ hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ value : int [1:22] 4 4 4 4 5 5 4 4 4 3 ...
## .. .. ..$ chroma : int [1:22] 4 4 4 4 8 1 4 4 3 3 . ..
## .. .. ..$ dry_hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ dry_value : int [1:22] 6 6 6 6 6 6 6 6 6 5 ...
## .. .. ..$ dry_chroma : int [1:22] 4 4 4 4 7 1 4 4 3 3 ...
## .. .. ..$ texture_class: Ord.factor w/ 21 levels "coarse sand"<..: 13 18 17 13 17 17 13 13 13 NA ...
## .. .. ..$ cf_class : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH_class : Ord.factor w/ 12 levels "ultra acid"<"extremely acid"<..: 3 3 3 3 3 3 3 4 NA NA ...
## .. .. ..$ distinctness : chr [1:22] "clear" "gradual" "gradual" "gradual" ...
## .. .. ..$ topography : chr [1:22] "smooth" "wavy" "wavy" "wavy" ...
## .. .. ..$ narrative : chr [1:22] "Ap--0 to 4 inches; brown (7.5YR 4/4) loam; weak medium granular structure; friable; common very fine, fine, and"| __truncated__ "Bw1--4 to 14 inches; dark yellowish brown (10YR 4/4) silty clay loam; weak medium subangular blocky structure; "| __truncated__ "Bw2--14 to 26 inches; dark yellowish brown (10YR 4/4) clay loam; weak medium subangular blocky structure; friab"| __truncated__ "Bw3--26 to 38 inches; brown (7.
..
## .. .. ..$ dry_hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ dry_value : int [1:22] 6 6 6 6 6 6 6 6 6 5 ...
## .. .. ..$ dry_chroma : int [1:22] 4 4 4 4 7 1 4 4 3 3 ...
## .. .. ..$ texture_class: Ord.factor w/ 21 levels "coarse sand"<..: 13 18 17 13 17 17 13 13 13 NA ...
## .. .. ..$ cf_class : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH_class : Ord.factor w/ 12 levels "ultra acid"<"extremely acid"<..: 3 3 3 3 3 3 3 4 NA NA ...
## .. .. ..$ distinctness : chr [1:22] "clear" "gradual" "gradual" "gradual" ...
## .. .. ..$ topography : chr [1:22] "smooth" "wavy" "wavy" "wavy" ...
## .. .. ..$ narrative : chr [1:22] "Ap--0 to 4 inches; brown (7.5YR 4/4) loam; weak medium granular structure; friable; common very fine, fine, and"| __truncated__ "Bw1--4 to 14 inches; dark yellowish brown (10YR 4/4) silty clay loam; weak medium subangular blocky structure; "| __truncated__ "Bw2--14 to 26 inches; dark yellowish brown (10YR 4/4) clay loam; weak medium subangular blocky structure; friab"| __truncated__ "Bw3--26 to 38 inches; brown (7. 5YR 4/4) loam; weak medium subangular blocky structure; friable; common fine roo"| __truncated__ ...
## .. .. ..$ hzID : chr [1:22] "1" "2" "3" "4" ...
## .. ..@ site :'data.frame': 3 obs. of 33 variables:
## .. .. ..$ id : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## .. .. ..$ soiltaxclasslastupdated: chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "1997-06-06 00:00:00+00"
## .. .. ..$ mlraoffice : int [1:3] 3 3 3
## .. .. ..$ series_status : chr [1:3] "established" "established" "established"
## .. .. ..$ family : chr [1:3] "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" "fine-loamy, mixed, active, nonacid, thermic oxyaquic udifluvents" "loamy, mixed, active, thermic, shallow typic hapludalfs"
## .. .. ..$ soilorder : chr [1:3] "inceptisols" "entisols" "alfisols"
## .. .. ..$ suborder : chr [1:3] "udepts" "fluvents" "udalfs"
## .. .. ..$ greatgroup : chr [1:3] "dystrudepts" "udifluvents" "hapludalfs"
## .
5YR 4/4) loam; weak medium subangular blocky structure; friable; common fine roo"| __truncated__ ...
## .. .. ..$ hzID : chr [1:22] "1" "2" "3" "4" ...
## .. ..@ site :'data.frame': 3 obs. of 33 variables:
## .. .. ..$ id : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## .. .. ..$ soiltaxclasslastupdated: chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "1997-06-06 00:00:00+00"
## .. .. ..$ mlraoffice : int [1:3] 3 3 3
## .. .. ..$ series_status : chr [1:3] "established" "established" "established"
## .. .. ..$ family : chr [1:3] "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" "fine-loamy, mixed, active, nonacid, thermic oxyaquic udifluvents" "loamy, mixed, active, thermic, shallow typic hapludalfs"
## .. .. ..$ soilorder : chr [1:3] "inceptisols" "entisols" "alfisols"
## .. .. ..$ suborder : chr [1:3] "udepts" "fluvents" "udalfs"
## .. .. ..$ greatgroup : chr [1:3] "dystrudepts" "udifluvents" "hapludalfs"
## . . .. ..$ subgroup : chr [1:3] "fluvaquentic dystrudepts" "oxyaquic udifluvents" "typic hapludalfs"
## .. .. ..$ tax_partsize : chr [1:3] "fine-loamy" "fine-loamy" "loamy"
## .. .. ..$ tax_partsizemod : logi [1:3] NA NA NA
## .. .. ..$ tax_ceactcl : chr [1:3] "active" "active" "active"
## .. .. ..$ tax_reaction : chr [1:3] NA "nonacid" NA
## .. .. ..$ tax_tempcl : chr [1:3] "thermic" "thermic" "thermic"
## .. .. ..$ originyear : logi [1:3] NA NA NA
## .. .. ..$ establishedyear : int [1:3] 1937 1904 1916
## .. .. ..$ descriptiondateinitial : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ descriptiondateupdated : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ benchmarksoilflag : int [1:3] 1 0 0
## .. .. ..$ statsgoflag : int [1:3] 1 1 1
## .. .. ..$ objwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .
. .. ..$ subgroup : chr [1:3] "fluvaquentic dystrudepts" "oxyaquic udifluvents" "typic hapludalfs"
## .. .. ..$ tax_partsize : chr [1:3] "fine-loamy" "fine-loamy" "loamy"
## .. .. ..$ tax_partsizemod : logi [1:3] NA NA NA
## .. .. ..$ tax_ceactcl : chr [1:3] "active" "active" "active"
## .. .. ..$ tax_reaction : chr [1:3] NA "nonacid" NA
## .. .. ..$ tax_tempcl : chr [1:3] "thermic" "thermic" "thermic"
## .. .. ..$ originyear : logi [1:3] NA NA NA
## .. .. ..$ establishedyear : int [1:3] 1937 1904 1916
## .. .. ..$ descriptiondateinitial : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ descriptiondateupdated : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ benchmarksoilflag : int [1:3] 1 0 0
## .. .. ..$ statsgoflag : int [1:3] 1 1 1
## .. .. ..$ objwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## . . .. ..$ recwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .. .. ..$ typelocstareaiidref : int [1:3] 6691 6706 6691
## .. .. ..$ typelocstareatypeiidref: int [1:3] 3 3 3
## .. .. ..$ soilseriesiid : int [1:3] 24628 1057 23800
## .. .. ..$ soilseriesdbiidref : int [1:3] 122 122 122
## .. .. ..$ grpiidref : int [1:3] 15801 15801 15801
## .. .. ..$ tax_minclass : chr [1:3] "mixed" "mixed" "mixed"
## .. .. ..$ subgroup_mod : chr [1:3] "fluvaquentic" "oxyaquic" "typic"
## .. .. ..$ greatgroup_mod : chr [1:3] "dystr" "udi" "hapl"
## .. .. ..$ drainagecl : chr [1:3] "somewhat poorly" "well" "well"
## .. .. ..$ ac : int [1:3] 1259224 216875 617848
## .. .. ..$ n_polygons : int [1:3] 40647 10387 34748
## .. ..@ sp :Formal class 'SpatialPoints' [package "sp"] with 3 slots
## .. .. .. ..@ coords : num [1, 1] 0
## .
. .. ..$ recwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .. .. ..$ typelocstareaiidref : int [1:3] 6691 6706 6691
## .. .. ..$ typelocstareatypeiidref: int [1:3] 3 3 3
## .. .. ..$ soilseriesiid : int [1:3] 24628 1057 23800
## .. .. ..$ soilseriesdbiidref : int [1:3] 122 122 122
## .. .. ..$ grpiidref : int [1:3] 15801 15801 15801
## .. .. ..$ tax_minclass : chr [1:3] "mixed" "mixed" "mixed"
## .. .. ..$ subgroup_mod : chr [1:3] "fluvaquentic" "oxyaquic" "typic"
## .. .. ..$ greatgroup_mod : chr [1:3] "dystr" "udi" "hapl"
## .. .. ..$ drainagecl : chr [1:3] "somewhat poorly" "well" "well"
## .. .. ..$ ac : int [1:3] 1259224 216875 617848
## .. .. ..$ n_polygons : int [1:3] 40647 10387 34748
## .. ..@ sp :Formal class 'SpatialPoints' [package "sp"] with 3 slots
## .. .. .. ..@ coords : num [1, 1] 0
## . . .. .. ..@ bbox : logi [1, 1] NA
## .. .. .. ..@ proj4string:Formal class 'CRS' [package "sp"] with 1 slot
## .. .. .. .. .. ..@ projargs: chr NA
## .. ..@ diagnostic :'data.frame': 0 obs. of 0 variables
## .. ..@ restrictions:'data.frame': 0 obs. of 0 variables
## $ competing :'data.frame': 1 obs. of 3 variables:
## ..$ series : chr "CHEWACLA"
## ..$ competing: chr "OAKBORO"
## ..$ family : chr "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts"
## $ geomcomp :'data.frame': 3 obs. of 9 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Interfluve : num [1:3] 1 0 0.182
## ..$ Crest : num [1:3] 0 0 0.0267
## ..$ Head Slope : int [1:3] 0 0 0
## ..$ Nose Slope : int [1:3] 0 0 0
## ..$ Side Slope : num [1:3] 0 0 0.791
## ..$ Base Slope : int [1:3] 0 1 0
## ..$ n : int [1:3] 3 1 187
## ..$ shannon_entropy: num [1:3] 0 0 0.368
## $ hillpos :'data.
. .. .. ..@ bbox : logi [1, 1] NA
## .. .. .. ..@ proj4string:Formal class 'CRS' [package "sp"] with 1 slot
## .. .. .. .. .. ..@ projargs: chr NA
## .. ..@ diagnostic :'data.frame': 0 obs. of 0 variables
## .. ..@ restrictions:'data.frame': 0 obs. of 0 variables
## $ competing :'data.frame': 1 obs. of 3 variables:
## ..$ series : chr "CHEWACLA"
## ..$ competing: chr "OAKBORO"
## ..$ family : chr "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts"
## $ geomcomp :'data.frame': 3 obs. of 9 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Interfluve : num [1:3] 1 0 0.182
## ..$ Crest : num [1:3] 0 0 0.0267
## ..$ Head Slope : int [1:3] 0 0 0
## ..$ Nose Slope : int [1:3] 0 0 0
## ..$ Side Slope : num [1:3] 0 0 0.791
## ..$ Base Slope : int [1:3] 0 1 0
## ..$ n : int [1:3] 3 1 187
## ..$ shannon_entropy: num [1:3] 0 0 0.368
## $ hillpos :'data. frame': 3 obs. of 8 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Toeslope : num [1:3] 0.963 0.786 0
## ..$ Footslope : num [1:3] 0.0366 0.2143 0
## ..$ Backslope : num [1:3] 0 0 0.636
## ..$ Shoulder : num [1:3] 0 0 0.227
## ..$ Summit : num [1:3] 0 0 0.138
## ..$ n : int [1:3] 82 14 247
## ..$ shannon_entropy: num [1:3] 0.0975 0.3228 0.5577
## $ mtnpos : logi FALSE
## $ terrace :'data.frame': 2 obs. of 5 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Tread : num [1:2] 0.979 1
## ..$ Riser : num [1:2] 0.0213 0
## ..$ n : int [1:2] 94 36
## ..$ shannon_entropy: num [1:2] 0.064 0
## $ flats :'data.frame': 2 obs. of 7 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Dip : num [1:2] 0.1569 0.0667
## ..$ Talf : num [1:2] 0.843 0.867
## .
frame': 3 obs. of 8 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Toeslope : num [1:3] 0.963 0.786 0
## ..$ Footslope : num [1:3] 0.0366 0.2143 0
## ..$ Backslope : num [1:3] 0 0 0.636
## ..$ Shoulder : num [1:3] 0 0 0.227
## ..$ Summit : num [1:3] 0 0 0.138
## ..$ n : int [1:3] 82 14 247
## ..$ shannon_entropy: num [1:3] 0.0975 0.3228 0.5577
## $ mtnpos : logi FALSE
## $ terrace :'data.frame': 2 obs. of 5 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Tread : num [1:2] 0.979 1
## ..$ Riser : num [1:2] 0.0213 0
## ..$ n : int [1:2] 94 36
## ..$ shannon_entropy: num [1:2] 0.064 0
## $ flats :'data.frame': 2 obs. of 7 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Dip : num [1:2] 0.1569 0.0667
## ..$ Talf : num [1:2] 0.843 0.867
## . .$ Flat : int [1:2] 0 0
## ..$ Rise : num [1:2] 0 0.0667
## ..$ n : int [1:2] 51 15
## ..$ shannon_entropy: num [1:2] 0.27 0.301
## $ pmkind :'data.frame': 6 obs. of 5 variables:
## ..$ series: chr [1:6] "CHEWACLA" "CHEWACLA" "CONGAREE" "CONGAREE" ...
## ..$ pmkind: chr [1:6] "Alluvium" "Residuum" "Alluvium" "Fluviomarine deposits" ...
## ..$ n : int [1:6] 207 1 72 13 1 264
## ..$ total : int [1:6] 208 208 86 86 86 264
## ..$ P : num [1:6] 0.9952 0.0048 0.8372 0.1512 0.0116 ...
## $ pmorigin :'data.frame': 24 obs. of 5 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ pmorigin: chr [1:24] "Igneous and metamorphic rock" "Sedimentary rock" "Granite and gneiss" "Mixed" ...
## ..$ n : int [1:24] 29 11 2 2 1 1 1 1 1 1 ...
## ..$ total : int [1:24] 51 51 51 51 51 51 51 51 51 51 ...
## ..$ P : num [1:24] 0.5686 0.2157 0.0392 0.0392 0.0196 ...
## $ mlra :'data.
.$ Flat : int [1:2] 0 0
## ..$ Rise : num [1:2] 0 0.0667
## ..$ n : int [1:2] 51 15
## ..$ shannon_entropy: num [1:2] 0.27 0.301
## $ pmkind :'data.frame': 6 obs. of 5 variables:
## ..$ series: chr [1:6] "CHEWACLA" "CHEWACLA" "CONGAREE" "CONGAREE" ...
## ..$ pmkind: chr [1:6] "Alluvium" "Residuum" "Alluvium" "Fluviomarine deposits" ...
## ..$ n : int [1:6] 207 1 72 13 1 264
## ..$ total : int [1:6] 208 208 86 86 86 264
## ..$ P : num [1:6] 0.9952 0.0048 0.8372 0.1512 0.0116 ...
## $ pmorigin :'data.frame': 24 obs. of 5 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ pmorigin: chr [1:24] "Igneous and metamorphic rock" "Sedimentary rock" "Granite and gneiss" "Mixed" ...
## ..$ n : int [1:24] 29 11 2 2 1 1 1 1 1 1 ...
## ..$ total : int [1:24] 51 51 51 51 51 51 51 51 51 51 ...
## ..$ P : num [1:24] 0.5686 0.2157 0.0392 0.0392 0.0196 ...
## $ mlra :'data. frame': 19 obs. of 4 variables:
## ..$ series : chr [1:19] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ mlra : chr [1:19] "129" "135A" "136" "133A" ...
## ..$ area_ac : int [1:19] 6166 3878 929362 128376 78429 59646 29004 13530 10366 2128 ...
## ..$ membership: num [1:19] 0.005 0.003 0.738 0.102 0.062 0.047 0.023 0.011 0.008 0.01 ...
## $ climate.annual :'data.frame': 24 obs. of 12 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:24] "Elevation (m)" "Effective Precipitation (mm)" "Frost-Free Days" "Mean Annual Air Temperature (degrees C)" ...
## ..$ minimum : num [1:24] 0 128.8 177 11.3 986 ...
## ..$ q01 : num [1:24] 7 216.4 188 12.9 1069 ...
## ..$ q05 : num [1:24] 34 247.4 196 13.5 1093 ...
## ..$ q25 : num [1:24] 125 312.2 208 14.9 1136 ...
## ..$ q50 : num [1:24] 192 349.8 218 15.7 1178 ...
## ..$ q75 : num [1:24] 248 441.2 227 16.
frame': 19 obs. of 4 variables:
## ..$ series : chr [1:19] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ mlra : chr [1:19] "129" "135A" "136" "133A" ...
## ..$ area_ac : int [1:19] 6166 3878 929362 128376 78429 59646 29004 13530 10366 2128 ...
## ..$ membership: num [1:19] 0.005 0.003 0.738 0.102 0.062 0.047 0.023 0.011 0.008 0.01 ...
## $ climate.annual :'data.frame': 24 obs. of 12 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:24] "Elevation (m)" "Effective Precipitation (mm)" "Frost-Free Days" "Mean Annual Air Temperature (degrees C)" ...
## ..$ minimum : num [1:24] 0 128.8 177 11.3 986 ...
## ..$ q01 : num [1:24] 7 216.4 188 12.9 1069 ...
## ..$ q05 : num [1:24] 34 247.4 196 13.5 1093 ...
## ..$ q25 : num [1:24] 125 312.2 208 14.9 1136 ...
## ..$ q50 : num [1:24] 192 349.8 218 15.7 1178 ...
## ..$ q75 : num [1:24] 248 441.2 227 16. 4 1276 ...
## ..$ q95 : num [1:24] 348 568.8 235 17.3 1392 ...
## ..$ q99 : num [1:24] 480 740.8 243 17.8 1575 ...
## ..$ maximum : num [1:24] 919 1382.8 300 19.7 2202 ...
## ..$ n : int [1:24] 32689 32689 32689 32689 32689 32689 32689 32689 8392 8392 ...
## $ climate.monthly :'data.frame': 72 obs. of 14 variables:
## ..$ series : chr [1:72] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:72] "ppt1" "ppt2" "ppt3" "ppt4" ...
## ..$ minimum : num [1:72] 61 64 81 63 60 78 83 74 68 53 ...
## ..$ q01 : num [1:72] 74 71 92 71 69 83 92 85 81 72 ...
## ..$ q05 : num [1:72] 82 73 98 75 72 89 100 89 86 76 ...
## ..$ q25 : num [1:72] 93 83 105 83 81 96 108 96 91 82 ...
## ..$ q50 : num [1:72] 105 107 120 88 92 101 116 102 98 86 ...
## ..$ q75 : num [1:72] 115 121 128 95 101 106 123 110 105 91 ...
## ..$ q95 : num [1:72] 131 135 137 111 111 117 133 129 118 100 ...
## .
4 1276 ...
## ..$ q95 : num [1:24] 348 568.8 235 17.3 1392 ...
## ..$ q99 : num [1:24] 480 740.8 243 17.8 1575 ...
## ..$ maximum : num [1:24] 919 1382.8 300 19.7 2202 ...
## ..$ n : int [1:24] 32689 32689 32689 32689 32689 32689 32689 32689 8392 8392 ...
## $ climate.monthly :'data.frame': 72 obs. of 14 variables:
## ..$ series : chr [1:72] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:72] "ppt1" "ppt2" "ppt3" "ppt4" ...
## ..$ minimum : num [1:72] 61 64 81 63 60 78 83 74 68 53 ...
## ..$ q01 : num [1:72] 74 71 92 71 69 83 92 85 81 72 ...
## ..$ q05 : num [1:72] 82 73 98 75 72 89 100 89 86 76 ...
## ..$ q25 : num [1:72] 93 83 105 83 81 96 108 96 91 82 ...
## ..$ q50 : num [1:72] 105 107 120 88 92 101 116 102 98 86 ...
## ..$ q75 : num [1:72] 115 121 128 95 101 106 123 110 105 91 ...
## ..$ q95 : num [1:72] 131 135 137 111 111 117 133 129 118 100 ...
## . .$ q99 : num [1:72] 149 144 147 122 125 133 143 142 137 109 ...
## ..$ maximum : num [1:72] 248 227 239 150 167 198 220 207 192 158 ...
## ..$ n : int [1:72] 32689 32689 32689 32689 32689 32689 32689 32689 32689 32689 ...
## ..$ month : Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## ..$ variable : Factor w/ 2 levels "Potential ET (mm)",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ soilweb.metadata:'data.frame': 19 obs. of 2 variables:
## ..$ product : chr [1:19] "block diagram archive" "component pedons" "KSSL snapshot" "MLRA membership" ...
## ..$ last_update: chr [1:19] "2019-12-17" "2020-12-08" "2020-03-13" "2020-07-14" ...
.$ q99 : num [1:72] 149 144 147 122 125 133 143 142 137 109 ...
## ..$ maximum : num [1:72] 248 227 239 150 167 198 220 207 192 158 ...
## ..$ n : int [1:72] 32689 32689 32689 32689 32689 32689 32689 32689 32689 32689 ...
## ..$ month : Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## ..$ variable : Factor w/ 2 levels "Potential ET (mm)",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ soilweb.metadata:'data.frame': 19 obs. of 2 variables:
## ..$ product : chr [1:19] "block diagram archive" "component pedons" "KSSL snapshot" "MLRA membership" ...
## ..$ last_update: chr [1:19] "2019-12-17" "2020-12-08" "2020-03-13" "2020-07-14" ...
Базовый шаблон ggplot
Для начала посмотрим, как можно показать суммарный экспорт по годам:
Базовый (минимально необходимый) шаблон построения графика через ggplot выглядит следующим образом:
ggplot(data = <DATA>) +
<GEOM_FUNCTION>(mapping = aes(<MAPPINGS>))
где:
-
DATA — источник данных (фрейм, тиббл) -
GEOM_FUNCTION — функция, отвечающая за геометрический тип графика (точки, линии, гистограммы и т. д.)
д.) -
MAPPINGS — перечень соответствий между переменными данных (содержащихся в DATA) и графическими переменными (координатами, размерами, цветами и т.д.)
Геометрические типы и преобразования
ggplot предлагает несколько десятков различных видов геометрий для отображения данных. С их полным перечнем можно познакомиться тут. Мы рассмотрим несколько наиболее употребительных, а геометрии, связанные со статистическими преобразованиями, оставим для следующей темы.
В первом примере мы отображали данные по экспорту за разные года, однако точечный тип не очень подходит для данного типа графика, поскольку он показывает динамику изменения. А это означает, что желательно соединить точки линиями. Для этого используем геометрию geom_line():
Поскольку в данном случае величина является агрегированной за год, более правильным может быть показ ее изменений в виде ступенчатого линейного графика, который получается через геометрию geom_step():
Можно совместить несколько геометрий, добавив их последовательно на график:
Если у нескольких геометрий одинаковые отображения, их можно вынести в вызов функции ggplot() (чтобы не дублировать):
Наглядность линейного графика можно усилить, добавив “заливку” области с использованием geom_area():
Для построения столбчатой диаграммы следует использовать геометрию geom_col(). Например, вот так выглядит структура экспорта продукции машиностроения из Евросоюза по ведущим партнерам:
Например, вот так выглядит структура экспорта продукции машиностроения из Евросоюза по ведущим партнерам:
trades %>%
dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col()
Развернуть диаграмму можно, используя функцию coord_flip():
Графические переменные и группировки
Графические переменные — это параметры, определяющие внешний вид символов. К ним относятся цвет (тон, насыщенность и светлота), размер, форма, ориентировка, внутренняя структура символа. В ggplot значения графических переменных могут быть едиными для всех измерений, а могут зависеть от величины измерений. С точки зрения управления здесь все просто: если вы хотите, чтобы какой-то графический параметр зависел от значения показателя, он должен быть указан внутри конструкции mapping = aes(...). Если необходимо, чтобы этот параметр был одинаковым для всех измерений, вы должны его указать внутри <GEOM_FUNCTION>(. ..)
..), то есть не передавать в mapping.
Для управления цветом, формой и размером (толщиной) графического примитива следует использовать параметры color, shape и size соответственно. Посмотрим, как они работают внутри и за пределами функции aes():
# один цвет для графика (параметр за пределами aes)
ggplot(trades_total) +
geom_line(mapping = aes(x = time, y = export), color = 'blue')
trade_russia = trades %>% dplyr::filter(partner == 'Russia')
ggplot(trade_russia) + # у каждой группы данных свой цвет (параметр внутри aes)
geom_line(mapping = aes(x = time, y = export, color = sitc06))
ggplot(trade_russia, mapping = aes(x = time, y = export, color = sitc06)) + # а теперь и с точками
geom_line() +
geom_point()
Аналогичным образом работает параметр формы значка:
# один значок для графика
ggplot(trades_total) +
geom_point(mapping = aes(x = time, y = export), shape = 15)
ggplot(trade_russia) + # у каждой группы данных свой значок
geom_point(mapping = aes(x = time, y = export, shape = sitc06))
Для изменения размера значка или линии используйте параметр size:
# изменение размера значка и линии
ggplot(trades_total, mapping = aes(x = time, y = export)) +
geom_point(size = 5) +
geom_line(size = 2)
Если вы используете зависимые от значений графические переменные и при этом хотите добавить на график еще одну геометрию (c постоянными параметрами), то вам необходимо сгруппировать объекты второй геометрии по той же переменной, по которой вы осуществляете разбиение в первой геометрии. Для этого используйте параметр
Для этого используйте параметр group:
Для изменения цвета столбчатых диаграмм следует использовать параметр fill, а цвет и толщина обводки определяются параметрами color и size:
trades %>%
dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col(fill = 'plum4', color = 'black', size = 0.2) +
coord_flip()
Цвет на столбчатых диаграммах можно использовать для отображения дополнительных переменных, например типа экспортируемой продукции. По умолчанию столбики будут образовывать стек
Если вам важно не абсолютное количество, а процентное соотношение величин, вы можете применить вид группировки position == 'fill:
Еще один вид группировки — это группировка по соседству. Чтобы использовать ее, применить метод position == 'dodge:
trade_russia %>%
dplyr::filter(time >= as. Date('2013-01-01')) %>%
ggplot(mapping = aes(x = time, y = export, fill = sitc06)) +
geom_col(color = 'black', size = 0.2, position = 'dodge')
Date('2013-01-01')) %>%
ggplot(mapping = aes(x = time, y = export, fill = sitc06)) +
geom_col(color = 'black', size = 0.2, position = 'dodge')
Системы координат
ggplot поддерживает множество полезных преобразований координат, таких как смена осей X и Y, переход к логарифмическим координатам и использование полярной системы вместо декартовой прямоугольной.
Смена переменных происходит благодаря уже знакомой нам функции coord_flip(). Рассмотрим, например, как изменилась структура экспорта/импорта по годам:
trades_type = trades %>%
group_by(sitc06, time) %>%
summarise(export = sum(export),
import = sum(import))
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5)
Поскольку объемы продукции различаются на порядки, для различимости малых объемов целесообразно перейти к логарифмической шкале. Для этого используем
Для этого используем scale_log_x() и scale_log_y():
Преобразование в полярную систему координат используется для того чтобы получить круговую секторную диаграмму Найтингейл (coxcomb chart):
Разумеется, здесь тоже можно использовать преобразование шкалы по оси Y (которая теперь отвечает за радиус). Применим правило квадратного корня, добавив вызов функции scale_y_sqrt():
Чтобы построить классическую секторную диаграмму, необходимо, чтобы угол поворота соответствовал величине показателя (оси Y), а не названию категории (оси X). Для этого при вызове функции coord_polar() следует указать параметр theta = 'y', а при вызове geom_col() оставить параметр x пустым:
trades %>%
dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as.Date('2017-01-01')) %>%
ggplot(mapping = aes(x = '', y = export, fill = partner), color = 'black', size = 0. 2) +
geom_col() +
coord_polar(theta = 'y')
2) +
geom_col() +
coord_polar(theta = 'y')
Названия осей и легенды
ggplot предоставляет ряд функций для аннотирования осей и легенды. Для этого можно использовать одну из следующих функций:
-
labs(...) модифицирует заголовок легенды для соответствующей графической переменной, либо заголовок/подзаголовок графика -
xlab(label) модифицирует подпись оси X -
ylab(label) модифицирует подпись оси Y -
ggtitle(label, subtitle = NULL) модифицирует заголовок и подзаголовок графика
Создадим подписи легенд, отвечающих за цвет и размер значка на графике соотношения импорта и экспорта разных видов продукции:
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) +
labs(color = "Вид продукции", size = 'Год')
Добавим заголовок и подзаголовок графика:
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0. 5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам')
5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам')
Изменим подписи осей:
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт')
Разметка осей
Первое, что вам скорее всего захочется убрать — это экспоненциальная запись чисел. На самом деле, эта запись не является параметром ggplot или стандартной системы graphics. Количество значащих цифр, после которых число автоматически представляется в экспоненциальном виде, управляется параметром scipen. Мы можем задать его достаточно большим, чтобы запретить переводить любые разумные числа в экспоненциальный вид:
options(scipen = 999)
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0. 5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт')
5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт')
Для управления разметкой осей необходимо использовать функции scale_x_continuous(), scale_y_continuous(), scale_x_log10(...), scale_y_log10(...), scale_x_reverse(...), scale_y_reverse(...), scale_x_sqrt(...), scale_y_sqrt(...), которые, с одной стороны, указывают тип оси, а с другой стороны — позволяют управлять параметрами сетки координат и подписями.
Для изменения координат линий сетки и подписей необходимо использовать, соответственно, параметры breaks и labels:
В данном случае, как раз, будет достаточно полезным параметр labels, поскольку метки можно сделать более компактными, поделив их на 1000 (и не забыть потом указать, что объемы теперь указаны не в миллионах, а в миллиардах долларов):
brks = seq(0, 500000, 100000)
ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) +
geom_point(alpha = 0. 5) +
scale_x_log10(breaks = brks, labels = brks / 1000) +
scale_y_log10(breaks = brks, labels = brks / 1000)
5) +
scale_x_log10(breaks = brks, labels = brks / 1000) +
scale_y_log10(breaks = brks, labels = brks / 1000)
Для обычной шкалы используйте функции scale_x_continuous() и scale_y_continuous():
Для того чтобы принудительно указать диапазоны осей и графических переменных, следует использовать функции lims(...), xlim(...) и ylim(...). Например, мы можем приблизиться в левый нижний угол графика, задав диапазон 0-200000 по обеим осям:
ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) +
geom_point(alpha = 0.5) +
xlim(0, 75000) +
ylim(0, 75000)
Функция lims() работает еще хитрее: она позволяет применять графические переменные только к ограниченному набору значений исходных данных. Например, таким путем я могу выделить на графике продукцию машиностроения:
ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) +
geom_point(alpha = 0. 5) +
lims(color = 'Machinery and transport equipment')
5) +
lims(color = 'Machinery and transport equipment')
Подписи и аннотации
С точки зрения ggplot текст на графике, отображающий входные данные, является одной из разновидностей геометрии. Размещается он с помощью функции geom_text(). Как и в случае с другими геометриями, параметры, зависящие от исходных данных, должны быть переданы внутри mapping = aes(...):
Выравнивание подписи относительно якорной точки (снизу, сверху, справа, слева) по горизонтали и вертикали управляется параметрами hjust и vjust, а смещения по осям X (в координатах графика) — параметрами nudge_x и nudge_y:
ggplot(data = trades_total, mapping = aes(x = time, y = export)) +
geom_area(alpha = 0.5) + # полигон с прозрачностью 0,5
geom_line() +
geom_point() +
geom_text(aes(label = floor(export / 1000)),
vjust = 0, nudge_y = 40000) # добавляем подписи
Подписи с фоновой плашкой добавляются через функцию geom_label(), которая имеет аналогичный синтаксис:
trades %>%
dplyr::filter(sitc06 == 'Machinery and transport equipment', time == as. Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col(fill = 'plum4', color = 'black', size = 0.2) +
coord_flip() +
geom_label(aes(y = export / 2, label = floor(export / 1000))) # добавляем подписи
Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col(fill = 'plum4', color = 'black', size = 0.2) +
coord_flip() +
geom_label(aes(y = export / 2, label = floor(export / 1000))) # добавляем подписи
Аннотации представляют собой объекты, размещаемые на графике вручную, и используемые, как правило, для выделения объектов и областей. Для размещения аннотаций используется функция annotate():
ggplot(data = trades_total, mapping = aes(x = time, y = export)) +
geom_area(alpha = 0.5) + # полигон с прозрачностью 0,5
geom_line() +
geom_point() +
geom_text(aes(label = floor(export / 1000)),
vjust = 0, nudge_y = 40000) +
annotate("text", x = as.Date('2009-01-01'), y = 550000, label = "Это провал", color = 'red')
Аннотировать можно не только подписями, но и регионами. Например, мы можем выделить область, которая соответствует импорту/экспорту продукции химической промышленности:
ggplot(trades_type, mapping = aes(x = export, y = import, color = sitc06, size = time)) +
annotate("rect", xmin = 100000, xmax = 250000, ymin = 75000, ymax = 175000, alpha = . 2, color = 'black', size = 0.1) +
geom_point(alpha = 0.5) +
annotate("text", x = 175000, y = 190000, label = "Chemicals", color = 'coral')
2, color = 'black', size = 0.1) +
geom_point(alpha = 0.5) +
annotate("text", x = 175000, y = 190000, label = "Chemicals", color = 'coral')
Фасеты
Фасеты представляют собой множество графиков, каждый из которых отображает свою переменную или набор значений. Для разбиения на фасеты используется функция facet_wrap(), которой необходимо передать переменную разбиения с тильдой. Например, рассмотрим изменение структуры импорта по годам:
brks = c(0, 50, 100, 150, 200)
trades %>%
dplyr::filter(sitc06 == 'Machinery and transport equipment') %>%
ggplot(mapping = aes(x = partner, y = import)) +
geom_col() +
scale_y_continuous(breaks = brks * 1e3, labels = brks) +
ggtitle('Импорт продукции машиностроения (мдрд долл. США)',
subtitle = 'Данные по ключевым партнерам') +
coord_flip() +
facet_wrap(~time)
Темы
Система ggplot интересна также тем, что для нее существует множество предопределенных “тем” или скинов для оформления графиков. Часть из них входит в состав самой библиотеки. Дополнительные темы можно установить через пакет ggthemes. Чтобы изменить тему оформления ggplot, достаточно прибавить в конце построения графика соответствующую функцию. Например, классическая черно-белая тема получается прибавлением функции
Часть из них входит в состав самой библиотеки. Дополнительные темы можно установить через пакет ggthemes. Чтобы изменить тему оформления ggplot, достаточно прибавить в конце построения графика соответствующую функцию. Например, классическая черно-белая тема получается прибавлением функции theme_bw():
ggplot(trades_type) +
geom_point(mapping = aes(x = export, y = import, color = sitc06, size = time), alpha = 0.5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт') +
theme_bw()
Контрольные вопросы и упражнения
Вопросы
- Назовите три основных компоненты шаблона построения графика в ggplot2.
- Как называются геометрии ggplot2, отвечающие за построение точек, линий и ступенчатых линий?
- Как называется геометрия ggplot2, отвечающая за построение столбчатой диаграммы?
- Как сделать так, чтобы графический параметр ggplot2 был постоянным для всех измерений?
- Как сделать так, чтобы графический параметр ggplot2 зависел от значения переменной?
- Перечислите названия параметров, отвечающих за цвет, размер, заливку и тип значка графического примитива.

- Если вы используете зависимые от значений графические переменные и при этом хотите добавить на график еще одну геометрию с постоянными параметрами, то как это можно реализовать?
- Перечислите названия режимов группировки столбчатых диаграмм и пути их реализации.
- Какая функция ggplot2 позволяет поменять местами оси координат?
- Перечислите типы шкал для осей координат, которые доступны в ggplot2.
- Назовите функцию, позволяющую перейти к полярной системе координат при построении графика в ggplot2.
- В чем отличие построения розы-диаграммы (coxcomb chart) и секторной диаграммы (pie chart) средствами ggplot2?
- Что делает функция
labs()? - Какие функции позволяют определить названия осей и заголовок графика?
- Что делает функция
lims()? - Как ограничить область построения графика заданным диапазоном значений координат?
- Как ограничить применение графических переменных только к определенным значениям измерений?
- Назовите геометрии, которые позволяют размещать подписи и подписи с плашками (фоном) на графиках ggplot2.

- Чем отличаются аннотации от геометрии подписей в ggplot? Какие виды аннотаций можно создавать?
- Каким образом можно построить фасетный график, на котором каждое изображение соответствует значению переменной? Каков синтаксис вызова соответствующей функции?
- Как поменять стиль отображения (тему) графика ggplot2?
- Как получить программный доступ к таблицам Евростата, не прибегая к закачке файлов? Какой пакет можно использовать для этого?
- Что является уникальным идентификатором таблицы в данных Евростата и как его узнать?
- Как преобразовать коды Евростата в загруженных таблицах в человеко-читаемые обозначения?
Упражнения
Постройте линейный график хода температуры , а также столбчатую диаграмму хода суммарной солнечной радиации в Екатеринбурге на примере данных NASA POWER, загруженных в разделе 6.3.
Подсказка: Для построения столбчатой диаграммы вам потребуется использовать функцию geom_col(), поскольку высота столбика отражает не встречаемость значения, а величину переменной. Также вам потребуется преобразовать таблицу среднемесячных величин к длинной форме, где название месяца будет отдельной переменной (тип — упорядоченный фактор).
Также вам потребуется преобразовать таблицу среднемесячных величин к длинной форме, где название месяца будет отдельной переменной (тип — упорядоченный фактор).
Загрузите таблицу данных по импорту/экспорту продуктов питания, напитков и табака с портала Евростата (с использованием пакета eurostat). Постройте линейный график изменения суммарных величин импорта и экспорта по данному показателю (у вас должно получиться 2 графика на одном изображении). Используйте цвет для разделения графиков. Добавьте текстовые подписи величин импорта и экспорта. Постройте также две круговых диаграммы, показывающих соотношение ведущих импортеров и экспортеров за последний имеющийся год. Сделайте сначала это отдельными графиками, а затем одним фасетным графиком (для этого потребуется привести таблицу к длинной форме).
Самсонов Т.Е. Визуализация и анализ географических данных на языке R. М. : Географический факультет МГУ, 2021. DOI: 10.5281/zenodo.901911
: Географический факультет МГУ, 2021. DOI: 10.5281/zenodo.901911
103 Виды и типы графиков на Forex, график баров, японских свечей, тиковый график
Используемые значения
Графики рынка forex обычно составляются в двух координатах - цены (откладывается по вертикальной оси) и времени (откладывается по горизонтальной оси). Иногда по вертикальной оси откладывается также график тикового объема.
Ось времени может иметь различный масштаб, который иногда называется интервалом, торговым периодом или таймфреймом (timeframe).
Традиционно в качестве таймфрейма используются следующие интервалы: год, месяц, неделя, день, 4 часа, 1 час, 30 минут, 15 минут, 5 минут, 1 минута, единичная котировка (тик).
Примечание: единичной котировкой или тиком является изменение цены маркетмейкером рынка переданное через информационные системы одновременно в виде двух новых цен покупки и продажи (Ask и Bid) . Подробнее см. раздел «Как формируются котировки».
Подробнее см. раздел «Как формируются котировки».
Поскольку график forex формируется по цене в определенный период времени, например, час, то в каждом периоде у цены есть 4 значения, которые, как правило, и наносят на график одновременно:
- цена открытия торгового периода (open) - цена на рынке, сложившаяся на начало торгового периода. Поскольку на начало торгового периода всегда существует 2 цены (на покупку и на продажу), то цена открытия обычно рассчитывается как среднее между Ask и Bid т.е. (Ask+Bid)/2. Фактически ценой на начало торгового периода является первая котировка данного периода.
- цена закрытия торгового периода (сlose) - цена на рынке, сложившаяся на конец торгового периода. Поскольку в конце торгового периода всегда существует 2 цены, то цена закрытия также обычно рассчитывается как среднее между Ask и Bid т.е. (Ask+Bid)/2; Фактически ценой на конец торгового периода является последняя котировка данного периода.
- максимальная цена торгового периода (high) - самая высокая цена на рынке Forex, сложившаяся за период (обычно используется Ask, поскольку Ask всегда больше Bid) ;
- минимальная цена торгового периода (low) - самая низкая цена на рынке Forex, сложившаяся за период (обычно используется Bid) ;
Иногда к этим четырем значениям в качестве самостоятельного индикатора на графике отображают тиковый объем.
- тиковый объем (tick volume) - количество тиков (изменений цены маркет-мейкеров) пришедших в информационную систему за данный период времени.
Виды отображения графиков
1. Тиковый график (Tick chart)
Тиковый график имеет самый мелкий масштаб - 1 тик (единичное котирование маркет-мейкером цен покупки и продажи). Это график котировок Bid и Ask, которые выглядят как столбцы на графике цен.
Максимум каждого отдельного столбца в тиковом графике - это котировка Ask, минимум каждого конкретного столбца - это котировка Bid.
Тиковый график как правило не используется для анализа рынка, поскольку его масштаб настолько мал, что не подходит для технического анализа. Однако тиковые графики эффективно используют для точного определения уровней поддержки и сопротивления, а также для того, чтобы повысить эффективность покупок и продаж, делая это на локальных минимумах и максимумах.
2. Линейный график (Line Chart)
Линейный график строится по одной из цен за периоды указанные выше. В большинстве случаев для этого используется цена закрытия (close) , однако также могут быть использованы цены открытия (open), максимальные цены за период (High) , минимальные цены за период (Low) или синтетические варианты: Median Price ([High + Low]/2) или Typical Price ( [High + Low + Close]/3).
Линейный график, по мнению трейдеров, обладает рядом преимуществ и недостатков.
Преимущества:
- удобство при поиске фигур технического анализа (паттернов).
- отсутствие избыточной информации
Недостатки:
- невозможно оценить, что происходило внутри торгового периода, были ли значительные подъемы или падения цен
- невозможно увидеть были ли гэпы (gaps) - ценовые разрывы между закрытием предыдущего и открытием последующего периода.
3. График баров (Bar chart), график интервальных гистограмм
При построении барового графика используются уже все 4 основные значения цены: открытие, максимум, минимум и закрытие (open, high, low, close) .
На графике баров каждый период обозначается вертикальной линией (представляющей собой диапазон колебания цен внутри периода), слева и справа от которой располагается по одной черте.
Каждый период, например час, выглядит следующим образом:
Верхний конец вертикальной черты показывает уровень максимальной цены, которую рынок достигал в данном периоде.
Соответственно, нижний конец вертикальной черты - минимальный уровень цены, который рынок достигал в течение данного периода.
Таким образом, вертикальная черта в целом представляет собой торговый диапазон периода (например, часа) или общие границы колебания цены внутри периода.
Черта слева представляет собой уровень цены, который был в начале периода и именуется ценой открытия (open).
Черта справа указывает уровень цены, который существовал на момент окончания периода (например, определенного часа) и называется ценой закрытия (close) .
Поскольку правая черта означает цену на начало периода (открытие периода), а левая - цену на конец периода (закрытие периода), то если левая черта выше правой, это означает что цена на рынке forex за это период упала. Если наоборот - выросла.
Преимущества:
- Можно примерно оценить, что происходило внутри торгового периода, были ли значительные подъемы или падения цен
- Можно определить наличие гэпов
Недостатки:
- Трудно с первого взгляда оценить, вырос рынок за период или нет.
- Невозможно определить характер движения внутри периода (нужно переходить на более мелкие масштабы).
3. Японские свечи (Japanese candlesticks)
График японских свечей схож по отображению и функциональности с баровым графиком, но более удобен для визуального восприятия.
При построении графика японских свечей также используются все 4 основные значения цены: открытие, максимум, минимум и закрытие (open, high, low, close) . Каждая отдельная свеча также как и на баровом графике означает определенный период времени, например, 1 час.
- Широкая часть свечи (прямоугольник) называется телом (real body или джиттай). Тело - это ценовой диапазон между ценами открытия и закрытия. Заполненное тело свечи означает, что цена закрытия была меньше цены открытия периода, т.е. за период цен в целом упали (черная свеча - «ин-сен»).
- Пустое тело свечи означает, что цена закрытия была больше цены открытия, т. е. цены внутри диапазона росли (белая свеча - «йо-сен»).
е. цены внутри диапазона росли (белая свеча - «йо-сен»).
- Линия над телом свечи называется верхней тенью (upper shadow или uwakage), а ее верхняя точка указывает максимум, который достигали цены внутри периода.
- Линия под телом свечи называется нижней тенью (lower shadow или shitakage) и ее нижняя точка - это минимум, который достигали цены внутри периода.
Примечание: тело как растущей, так и падающей свечи в различных программах технического анализа могут быть различных цветов. В оригинале красная свеча означает рост, черная - падение. Однако, согласно легенде, первые свечные графики попали в Америку из Японии на ксерокопиях, где падающая свеча осталась черной, а растущая превратилась в белую. Существуют и другие комбинации, например, зеленая растущая, а красная падающая. Обычно действуют следующие правила: заполненная свеча - падающая, а свеча цвета фона - растущая или падающая свеча темнее растущей.
Существуют и другие типы графиков.
- Объемные японские свечи (Candlevolume)
- Эквиобъемные графики (Equivolume).
- Пунктоцифровые графики (Point and Figure, так же называемые XO, или кресты-нули)
- Графики прорыва 3-х линий (Three-Line Break)
- графики Ренко (Renko)
- графики Каги (Kagi)
Примечание:
Будьте внимательны, зачастую на вертикальной оси (цены) используется не арифметическая, а логарифмическая шкала. Она получила распространение при анализе долгосрочных тенденций, когда цена валют на Forex может меняться на десятки процентов. Если на арифметической шкале расстояния между делениями цены на оси одинаковы, то на логарифмической шкале расстояние между делениями отражает одинаковые в процентах изменения цены.
Графические уравнения с программой «Пошаговое решение математических задач»
Язык математики особенно эффективен для представления отношений
между двумя или более переменными. В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.
Мы можем представить эту взаимосвязь как
В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.
Мы можем представить эту взаимосвязь как
- 1. Словесное предложение:
Пройденное расстояние в милях равно сороккратному количеству пройденных часов. - 2.Уравнение:
d = 40р. - 3. Таблица значений.
- 4. График, показывающий зависимость между временем и расстоянием.
Мы уже использовали словесные предложения и уравнения для описания таких отношений;
в этой главе мы будем иметь дело с табличным и графическим представлениями.
7.1 РЕШЕНИЕ УРАВНЕНИЙ ОТ ДВУХ ПЕРЕМЕННЫХ
ЗАКАЗАННЫЕ ПАРЫ
Уравнение d = 40f объединяет расстояние d для каждого времени t. Например,
, если t = 1, то d = 40
, если t = 2, то d = 80
, если t = 3, то d = 120
и так далее.
Пара чисел 1 и 40, рассматриваемая вместе, называется решением
уравнение d = 40r, потому что когда мы подставляем 1 вместо t и 40 вместо d в уравнении,
мы получаем верное утверждение. Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро. Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты.При этом соглашении решения
Уравнение d - 40t - это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны
Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро. Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты.При этом соглашении решения
Уравнение d - 40t - это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны
(0,0), (1,40), (2,80), (3,120), (4,160) и (5,200)
Такие пары иногда отображаются в одной из следующих табличных форм.
В любом конкретном уравнении с двумя переменными, когда мы присваиваем значение одной
переменных определяется значение другой переменной и, следовательно,
зависит от первого.Удобно говорить о переменной, связанной с
первый компонент упорядоченной пары как независимая переменная и переменная
связанный со вторым компонентом упорядоченной пары как зависимая переменная. Если в уравнении используются переменные x и y, подразумевается, что заменить -
элементы для x являются первыми компонентами и, следовательно, x - независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения
Если в уравнении используются переменные x и y, подразумевается, что заменить -
элементы для x являются первыми компонентами и, следовательно, x - независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения
, подставив конкретное значение одной переменной в уравнение (1) и решив для
другая переменная.
Пример 1
Найдите недостающий компонент, чтобы заказанная пара стала решением для
2x + y = 4
а. (0 ,?)
г. (1 ,?)
г. (2 ,?)
Решение
, если x = 0, то 2 (0) + y = 4
y = 4
если x = 1, то 2 (1) + y = 4
y = 2
, если x = 2, то 2 (2) + y = 4
y = 0
Три пары теперь могут отображаться как три упорядоченные пары
(0,4), (1,2) и (2,0)
или в табличной форме
ЯВНО ВЫРАЖАЮЩИЙ ПЕРЕМЕННУЮ
Мы можем добавить -2x к обоим членам 2x + y = 4, чтобы получить
-2x + 2x + y = -2x + 4
y = -2x + 4
В уравнении (2), где y есть само по себе, мы говорим, что y явно выражается через
из х. Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
Переменная.
Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
Переменная.
Например, в уравнении (2) выше
, если x = 0, то y = -2 (0) + 4 = 4
, если x = 1, то y = -2 (1) + 4 = 2
, если x = 2, то y = -2 (2) + 4 = 0
Мы получаем те же пары, что и с помощью уравнения (1)
(0,4), (1,2) и (2,0)
Мы получили уравнение (2) добавлением одинаковой величины -2x к каждому члену
уравнения (1), таким образом получая y отдельно.В общем, мы можем написать эквивалент
уравнения с двумя переменными, используя свойства, которые мы ввели в главе 3,
где мы решали уравнения первой степени с одной переменной.
Уравнения эквивалентны, если:
- Одно и то же количество прибавляется к равным количествам или вычитается из них.
- Равные количества умножаются или делятся на одинаковое ненулевое количество.
Пример 2
Решите 2y - 3x = 4 явно для y через x и получите решения для x = 0,
х = 1 и х = 2.
Решение
Во-первых, добавляя 3x к каждому члену, мы получаем
2y - 3x + 3x = 4 + 3x
2y = 4 + 3x (продолжение)
Теперь, разделив каждый член на 2, получаем
В этой форме мы получаем значения y для заданных значений x следующим образом:
В этом случае три решения: (0, 2), (1, 7/2) и (2, 5).
ОБОЗНАЧЕНИЕ ФУНКЦИЙ
Иногда мы используем специальные обозначения для наименования второго компонента упорядоченного
пара, которая связана с указанным первым компонентом.Символ f (x), который часто
используется для обозначения алгебраического выражения в переменной x, также может использоваться для обозначения
значение выражения для конкретных значений x. Например, если
f (x) = -2x + 4
, где f (x) играет ту же роль, что и y в уравнении (2) на странице 285, тогда f (1)
представляет значение выражения -2x + 4, когда x заменяется на 1
f (l) = -2 (1) + 4 = 2
Аналогично
f (0) = -2 (0) + 4 = 4
и
f (2) = -2 (2) + 4 = 0
Символ f (x) обычно называют обозначением функции.
Пример 3
Если f (x) = -3x + 2, найти f (-2) и f (2).
Решение
Замените x на -2, чтобы получить
f (-2) = -3 (-2) + 2 = 8
Замените x на 2, чтобы получить
f (2) = -3 (2) + 2 = -4
7.2 ГРАФИК ЗАКАЗАННЫХ ПАР
В разделе 1.1 мы увидели, что каждое число соответствует точке в строке. Simi-
Как правило, каждая упорядоченная пара чисел (x, y) соответствует точке на плоскости. К
граф упорядоченной пары чисел, мы начинаем с построения пары перпендикулярных
числовые линии, называемые осями.Горизонтальная ось называется осью x, вертикальная ось
называется осью Y, а их точка пересечения называется началом координат. Эти топоры
разделите плоскость на четыре квадранта, как показано на рисунке 7.1.
Теперь мы можем присвоить упорядоченную пару чисел точке на плоскости, указав
на перпендикулярное расстояние точки от каждой из осей. Если первый
составляющая положительная, точка лежит правее вертикальной оси; если отрицательный, это
лежит слева. Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.
Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.
Пример 1
График (3, 2), (-3, 2), (-3, -2) и (3, -2) в прямоугольной системе координат.
Решение
График (3, 2) находится на 3 единицы правее
ось y и 2 единицы над осью x;
график (-3,2) лежит на 3 единицы слева от
ось y и на 2 единицы выше оси x;
график (-3, -2) лежит на 3 единицы слева от
ось y и 2 единицы ниже оси x;
график (3, -2) лежит на 3 единицы правее
по оси Y и на 2 единицы ниже оси X.
Расстояние y, на котором точка расположена от оси x, называется ординатой.
точки, а расстояние x, на котором точка расположена от оси y, называется
абсцисса точки. Абсцисса и ордината вместе называются прямоугольником.
Гулярные или декартовы координаты точки (см. рисунок 7.2).
7.3 ИЗОБРАЖЕНИЕ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
В разделе 7.1 мы увидели, что решение уравнения с двумя переменными является упорядоченным
пара. В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
у = х + 2
, положив x равным 0, -3, -2 и 3. Затем
для x = 0, y = 0 + 2 = 2
для x = 0, y = -3 + 2 = -1
для x = -2, y = -2 + 2-0
для x = 3, y = 3 + 2 = 5
и получаем решения
(0,2), (-3, -1), (-2,0) и (3,5)
, который может отображаться в табличной форме, как показано ниже.
Если мы изобразим точки, определенные этими
упорядоченные пары и провести прямую через
их, мы получаем график всех решений
y = x + 2, как показано на рисунке 7.3. То есть,
каждое решение y = x + 2 лежит на прямой,
и каждая точка на линии является решением
у = х + 2.
Графики уравнений первой степени в двух
переменные всегда прямые; следовательно,
такие уравнения также называются линейными
уравнения.
В приведенном выше примере значения, которые мы использовали для
x были выбраны случайным образом; мы могли бы использовать
любые значения x, чтобы найти решения уравнения.Графики любых других упорядоченных пар, которые являются решениями уравнения, также будут
быть на линии, показанной на рисунке 7.3. Фактически, каждое линейное уравнение с двумя переменными
имеет бесконечное количество решений, график которых лежит на прямой. Однако мы только
нужно найти два решения, потому что для определения
прямая линия. Третий балл можно получить как проверку.
Для построения графика уравнения первой степени:
- Постройте набор прямоугольных осей, показывающих масштаб и переменную, представляющую
отправляется каждой осью.
- Найдите две упорядоченные пары, которые являются решениями уравнения для построения графика
присвоение любого удобного значения одной переменной и определение соответствующего
значение другой переменной.
- Изобразите эти упорядоченные пары.

- Проведите через точки прямую линию.
- Проверьте, построив график третьей упорядоченной пары, которая является решением уравнения и
убедитесь, что он лежит на линии.
Пример 1
Постройте уравнение y = 2x - 6.
Решение
Сначала мы выбираем любые два значения x, чтобы найти соответствующие значения y.
Мы будем использовать 1 и 4 для x.
Если x = 1, y = 2 (1) - 6 = -4
, если x = 4, y = 2 (4) - 6 = 2
Таким образом, два решения уравнения:
(1, -4) и (4, 2).
Затем мы строим график этих упорядоченных пар и проводим прямую линию через точки, как показано
на рисунке. Мы используем стрелки, чтобы показать, что
линия тянется бесконечно далеко в обоих направлениях.
Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать в качестве проверки:
, если x = 5, y = 2 (5) -6 = 4
Затем отметим, что график (5, 4) также лежит на линии
. Чтобы найти решения уравнения, как мы уже отмечали, часто проще всего сначала решить
явно для y через x.
Пример 2
График x + 2y = 4.
Решение
Сначала решаем y через x, чтобы получить
Теперь мы выбираем любые два значения x, чтобы найти соответствующие значения y. Мы будем использовать
2 и 0 для x.
Таким образом, два решения уравнения: (2, 1) и (0, 2).
Затем мы графически отображаем эти упорядоченные пары и
проведите прямую через точки, как
показано на рисунке.
Любая третья упорядоченная пара, удовлетворяющая
уравнение можно использовать как проверку:
Затем отметим, что график (-2, 3) также
лежит на линии.
ОСОБЫЕ СЛУЧАИ ЛИНЕЙНЫХ УРАВНЕНИЙ
Уравнение y = 2 можно записать как
0x + y = 2
и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при x равен 0. Некоторые
решения 0x + y = 2 равны
(1,2), (-1,2) и (4,2)
Фактически, любая упорядоченная пара вида (x, 2) является
решение (1). Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.
Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.
Аналогично, уравнение, такое как x = -3, может
записывается как
х + 0у = -3
и может рассматриваться как линейное уравнение в двух
переменные, у которых коэффициент при y равен 0.
Некоторые решения x + 0y = -3 являются
(-3, 5), (-3, 1) и (-3, -2). Фактически любой
упорядоченная пара вида (-3, y) является решением
из (2). Графическое изображение решений дает вертикальную
линии, как показано на рисунке 7.5.
Пример 3
График
а. y = 3
б. х = 2
Решение
а. Мы можем записать y = 3 как Ox + y = 3.
Некоторые решения: (1, 3), (2,3) и (5, 3).
б. Мы можем записать x = 2 как x + Oy = 2.
Некоторые решения: (2, 4), (2, 1) и (2, -2).
7.4 МЕТОД ПЕРЕСЕЧЕНИЯ ГРАФИКА
В Разделе 7.3 мы присвоили значения x в уравнениях с двумя переменными, чтобы найти
соответствующие значения y. Решения уравнения с двумя переменными, которые
обычно легче всего найти те, в которых первый или второй компонент
0. Например, если мы подставим 0 вместо x в уравнение
Решения уравнения с двумя переменными, которые
обычно легче всего найти те, в которых первый или второй компонент
0. Например, если мы подставим 0 вместо x в уравнение
3x + 4y = 12
у нас
3 (0) + 4y = 12
y = 3
Таким образом, решением уравнения (1) является (0, 3).Мы также можем найти упорядоченные пары, которые
решения уравнений с двумя переменными путем присвоения значений y и определения
соответствующие значения x. В частности, если мы подставим 0 вместо y в уравнение (1), мы
получить
3x + 4 (0) = 12
x = 4
и второе решение уравнения (4, 0). Теперь мы можем использовать упорядоченные пары
(0, 3) и (4, 0) для построения графика уравнения (1). График представлен на рисунке 7.6. Уведомление
что линия пересекает ось x в точке 4 и ось y в точке 3. По этой причине число
4 называется пересечением по оси x графа, а число 3 - точкой пересечения по оси y.
Этот метод построения графика линейного уравнения называется перехватом. метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
Пример 1
График 2x - y = 6 методом пересечения.
Решение
Мы находим точку пересечения с x, подставляя 0 вместо y в уравнение, чтобы получить
2x - (0) = 6
2x = 6
x = 3
Теперь мы находим точку пересечения по оси Y, подставляя
для x в уравнении, чтобы получить
2 (0) - y = 6
-y = 6
y = -6
Упорядоченные пары (3, 0) и (0, -6) являются решениями 2x - y = 6.Графическое изображение этих
точки и соединив их прямой линией, получим график 2x - y = 6.
Если график пересекает оси в или около начала координат, метод перехвата не работает.
удовлетворительно. Затем мы должны построить график упорядоченной пары, которая является решением уравнения
и чей график не является началом координат или не слишком близок к началу координат.
Пример 2
График y = 3x.
Решение
Мы можем заменить 0 на x и найти
y = 3 (0) = 0
Аналогичным образом, заменив 0 на y, мы получим
0 = 3.x, x = 0
Таким образом, 0 является одновременно точкой пересечения по оси x и точкой пересечения с y.
Так как одной точки недостаточно для графического = 3x, мы прибегаем к методам, описанным в
Раздел 7.3. Выбирая любое другое значение для x, скажем 2, мы получаем
у = 3 (2) = 6
Таким образом, (0, 0) и (2, 6) являются решениями
уравнение. График y = 3x показан на
верно.
7,5 НАКЛОН ЛИНИИ
ФОРМУЛА НАКЛОНА
В этом разделе мы изучим важное свойство линии.Мы назначим
число к линии, которую мы называем уклоном, что даст нам меру "крутизны"
или «направление» линии.
Часто бывает удобно использовать специальные обозначения для различения прямоугольников.
Гулярные координаты двух разных точек. Мы можем обозначить одну пару координат
на (x 1 , y 1 (читается «x sub one, y sub one»), связанный с точкой P 1 , и второй
пара координат по (x 2 , y 2 ), связанная со второй точкой P 2 , как показано на рисунке
7. 7. Обратите внимание на рис. 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y 2 - y 1 , а изменение по горизонтали (или
расстояние по горизонтали) составляет x 2 - x 1 .
7. Обратите внимание на рис. 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y 2 - y 1 , а изменение по горизонтали (или
расстояние по горизонтали) составляет x 2 - x 1 .
Отношение вертикального изменения к горизонтальному называется крутизной
линия, содержащая точки P 1 и P 2 . Это соотношение обычно обозначают m. Таким образом,
Пример 1
Найдите наклон прямой, содержащей два
точки с координатами (-4, 2) и (3, 5) как
показано на рисунке справа. Решение
Обозначим (3, 5) как (x 2 , y 2 ) и (-4, 2)
как (x 1 , y 1 ). Подставляя в уравнение (1)
дает
Обратите внимание, что мы получим тот же результат, если подставим -4 и 2 вместо x 2 и y 2 и 3 и
5 для x 1 и y 1
Линии с различным уклоном показаны на Рисунке 7. 8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y 2 - y 1 равно нулю для любых двух
точек, а наклон линии просто
8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y 2 - y 1 равно нулю для любых двух
точек, а наклон линии просто
Также обратите внимание (рисунок 7.8c), что, поскольку все точки на вертикали имеют одинаковое значение x,
x 2 - x 1 равняется нулю для любых двух точек. Однако
не определено, поэтому вертикальная линия не имеет наклона.
ПАРАЛЛЕЛЬНЫЕ И ПЕРПЕНДИКУЛЯРНЫЕ ЛИНИИ
Рассмотрим линии, показанные на рисунке 7.9. Линия l 1 имеет наклон m 1 = 3, а линия l 2 имеет
уклон м 2 = 3. В данном случае
Эти линии никогда не пересекаются и называются параллельными линиями. Теперь рассмотрим строки
показано на рисунке 7.10. Линия l 1 имеет наклон m 1 = 1/2, а прямая l 2 имеет наклон m 2 = -2. В данном случае
В данном случае
Эти линии пересекаются, образуя прямой угол, и называются перпендикулярными линиями.
Как правило, если две линии имеют уклон и м2:
а. Линии параллельны, если они имеют одинаковый наклон, то есть
если m 1 = m 2 .
г. Линии перпендикулярны, если произведение их уклонов
равно -1, то есть если m 1 * m 2 = -1.
7.6 УРАВНЕНИЯ ПРЯМЫХ ЛИНИЙ
ФОРМА POINT-SLOPE
В разделе 7.5 мы нашли наклон прямой по формуле
Допустим, мы знаем, что линия проходит через точку (2, 3) и имеет наклон 2.Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.1а), наклоном
формула
Таким образом, уравнение (1) - это уравнение прямой, проходящей через точку (2, 3), и
имеет уклон 2.
В общем, допустим, что мы знаем, что линия проходит через точку P 1 (x 1 , y 1 и имеет
уклон м. Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона
Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона
Уравнение (2) называется формой точечного уклона для линейного уравнения.В уравнении (2),
m, x 1 и y 1 известны, а x и y - переменные, которые представляют координаты
любая точка на линии. Таким образом, если нам известен наклон линии и точки на
линии, мы можем найти уравнение линии, используя уравнение (2).
Пример 1
Линия имеет наклон -2 и проходит через точку (2, 4). Найдите уравнение прямой.
Решение
Замените -2 вместо m и (2, 4) вместо (x 1 , y 1 ) в уравнении (2)
Таким образом, прямая с наклоном -2, проходящая через точку (2, 4), имеет уравнение
у = -2х + 8.Мы могли бы также записать уравнение в эквивалентной форме y + 2x = 8,
2x + y = 8 или 2x + y - 8 = 0.
ФОРМА НАКЛОНА
Теперь рассмотрим уравнение прямой с наклоном m и точкой пересечения оси y b, как показано на
Рисунок 7. 12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного
уравнение, имеем
12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного
уравнение, имеем
y - b = m (x - 0)
y - b = mx
или
y = mx + b
Уравнение (3) называется формой пересечения наклона
для линейного уравнения.Наклон и пересечение по оси Y
можно получить непосредственно из уравнения в
эта форма.
Пример 2 Если линия имеет уравнение
, то наклон линии должен быть -2, а точка пересечения оси Y - 8. Аналогично,
график
г = -3x + 4
имеет наклон -3 и точку пересечения по оси Y 4; и график
имеет наклон 1/4 и точку пересечения по оси Y -2.
Если уравнение не записано в форме x = mx + b, и мы хотим знать наклон
и / или точку пересечения с y, мы переписываем уравнение, решая относительно y через x.
Пример 3
Найдите наклон и точку пересечения оси Y 2x - 3y = 6.
Решение
Сначала мы решаем y в терминах x, добавляя -2x к каждому члену.
2x - 3y - 2x = 6 - 2x
- 3y = 6 - 2x
Теперь, разделив каждого члена на -3, мы получим
Сравнивая это уравнение с формой y = mx + b, отметим, что наклон m (величина
коэффициент при x) равен 2/3, а точка пересечения оси y равна -2.
7.7 ПРЯМАЯ ВАРИАЦИЯ
Частный случай уравнения первой степени с двумя переменными дается
y = kx (k - постоянная)
Такая связь называется прямой вариацией.Мы говорим, что переменная y изменяется
непосредственно как x.
Пример 1
Мы знаем, что давление P в жидкости изменяется прямо пропорционально глубине d ниже
поверхность жидкости. Мы можем обозначить это соотношение в символах как
P =
кД В прямом варианте, если мы знаем набор условий для двух переменных, и если
мы также знаем другое значение для одной из переменных, мы можем найти значение
вторая переменная для этого нового набора условий.
В приведенном выше примере мы можем решить для константы k, чтобы получить
Поскольку отношение P / d является постоянным для каждого набора условий, мы можем использовать соотношение
для решения задач, связанных с прямым изменением.
Пример 2
Если давление P напрямую зависит от глубины d и P = 40, когда d = 10, найдите P, когда
d = 15.
Решение
Поскольку отношение P / d является постоянным, мы можем подставить значения для P и d и получить
пропорция
Таким образом, P = 60 при d = 15.
7,8 НЕРАВЕНСТВА В ДВУХ ПЕРЕМЕННЫХ
В разделах 7.3 и 7.4 мы построили уравнения для двух переменных. В этом разделе мы
построит график неравенств по двум переменным. Например, рассмотрим неравенство
у ≤ -x + 6
Решения - это упорядоченные пары чисел, которые «удовлетворяют» неравенству.То есть,
(a, b) является решением неравенства, если неравенство является истинным утверждением после того, как мы
заменим a на x и b на y.
Пример 1
Определите, является ли данная упорядоченная пара решением y = -x + 6.
а. (1, 1)
б. (2, 5)
Решение
Упорядоченная пара (1, 1) является решением, потому что, когда 1 заменяется на x, а 1
подставляем вместо y, получаем
(1) = - (1) + 6, или 1 = 5
, что является правдой. С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем
С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем
(5) = - (2) + 6, или 5 = 4
, что является ложным заявлением.
Чтобы построить график неравенства y = -x + 6, сначала построим график уравнения y = -x + 6
показано на рисунке 7.13. Обратите внимание, что (3, 3), (3, 2), (3, 1), (3, 0) и т. Д., Связанные
с точками, находящимися на линии или под ней, являются решениями неравенства
y = -x + 6, тогда как (3,4), (3, 5) и (3,6), связанные с точками над
линии не являются решениями неравенства. Фактически, все упорядоченные пары, связанные с
точки на линии или ниже являются решениями y = - x + 6. Таким образом, каждая точка на или
под чертой находится на графике.Мы представляем это, закрашивая область под
линия (см. рисунок 7.14).
В общем, чтобы построить график неравенства первой степени с двумя переменными в виде
Ax + By = C или Ax + By = C, сначала строим график уравнения Ax + By = C и
затем определите, какая полуплоскость (область выше или ниже линии) содержит
решения. Затем закрашиваем эту полуплоскость. Всегда можно определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.В таком случае закрашиваем полуплоскость, содержащую контрольную точку; иначе,
закрашиваем другую полуплоскость. Часто (0, 0) - удобная контрольная точка.
Затем закрашиваем эту полуплоскость. Всегда можно определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.В таком случае закрашиваем полуплоскость, содержащую контрольную точку; иначе,
закрашиваем другую полуплоскость. Часто (0, 0) - удобная контрольная точка.
Пример 2
График 2x + 3y = 6
Решение
Сначала построим линию 2x + 3y = 6 (см. График a). Используя начало координат как контрольную точку,
мы определяем, является ли (0, 0) решением 2x + 3y ≥ 6. Поскольку утверждение
2 (0) + 3 (0) = 6
ложно, (0, 0) не является решением и мы закрашиваем полуплоскость, не содержащую
начало координат (см. график b).
Когда линия Ax + By = C проходит через начало координат, (0, 0) не является допустимым тестом
точка, поскольку она находится на линии.
Пример 3
График y = 2x.
Решение
Начнем с построения линии y = 2x (см. График a). Поскольку линия проходит через
начало координат, мы должны выбрать другую точку не на линии в качестве нашей тестовой точки. Мы будем
используйте (0, 1). Поскольку выписка
(1) = 2 (0)
верно, (0, 1) - решение, и мы закрашиваем полуплоскость, содержащую (0, 1) (см.
график б).
Если символ неравенства - ', точки на графике Ax + By = C
не являются решениями неравенства. Затем мы используем пунктирную линию для графика
Ax + By = C.
РЕЗЮМЕ ГЛАВЫ
Решение уравнения с двумя переменными - это упорядоченная пара чисел. в
упорядоченная пара (x, y), x называется первым компонентом, а y называется вторым
компонент. Для уравнения с двумя переменными переменная, связанная с первой
компонент решения называется независимой переменной, а переменная
связанный со вторым компонентом, называется зависимой переменной.Обозначение функции f (x) используется для обозначения алгебраического выражения в x. Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.
Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.
Пересечение двух перпендикулярных осей в системе координат называется
происхождение системы, и каждая из четырех областей, на которые делится плоскость
называется квадрантом. Компоненты упорядоченной пары (x, y), связанной с
точки на плоскости называются координатами точки; x называется абсциссой
точки, а y называется ординатой точки.
График уравнения первой степени с двумя переменными представляет собой прямую линию. То есть каждый
упорядоченная пара, которая является решением уравнения, имеет график, лежащий на линии, и
каждая точка в строке связана с упорядоченной парой, которая является решением
уравнение.
Графики любых двух решений уравнения с двумя переменными могут быть использованы для
получить график уравнения. Однако два решения уравнения в двух
переменные, которые обычно легче всего найти, - это те, в которых либо первая, либо
второй компонент равен 0. Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y, называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y, называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
Наклон прямой, содержащей точки P 1 (x 1 , y 1 ) и P 2 (x 2 , y 2 ), определяется как
Две прямые параллельны, если они имеют одинаковый наклон (m 1 = m 2 ).
Две прямые перпендикулярны, если произведение их наклонов равно - l (m 1 * m 2 = -1).
Форма точки-наклона прямой с наклоном m, проходящей через точку (x 1 , y 1 )
это
y - y 1 - m (x - x 1 )
Форма пересечения наклона линии с наклоном m и точкой пересечения y b равна
y = mx + b
Взаимосвязь, определяемая уравнением вида
y = kx (k постоянная)
называется прямой вариацией.
Решением неравенства с двумя переменными является упорядоченная пара чисел, которая,
при подстановке в неравенство делает неравенство истинным утверждением. В
График линейного неравенства от двух переменных представляет собой полуплоскость.
Символы, представленные в этой главе, находятся на внутренней стороне передней обложки.
Графическое изображение линейных уравнений: примеры | Purplemath
Purplemath
Пока вы делаете свою работу аккуратно и упорядоченно, у вас не должно возникнуть особых проблем с построением графиков линейных уравнений.Вот еще несколько примеров.
График
y = (–5/3) x - 2
Сначала сделаю Т-диаграмму. Поскольку я умножаю переменную x на дробь, знаменателем которой является 3, я выберу значения x , кратные 3. Таким образом, когда я подставлю свое значение для x , знаменатель будет отмените, и мне не придется иметь дело с дробями.
Таким образом, когда я подставлю свое значение для x , знаменатель будет отмените, и мне не придется иметь дело с дробями.
MathHelp.com
Затем я нанесу свои точки и нарисую свой график:
Здесь переменная x умножается на большее значение; он умножается на 5.Так что я должен ожидать, что мои значения y будут расти довольно быстро. Это означает, что я должен ожидать довольно «высокого» графика.
Сначала сделаю Т-диаграмму.
Это уравнение является примером ситуации, в которой вы, вероятно, захотите обратить особое внимание на выбранные вами значения x . Поскольку x умножается на относительно большое значение, значения y быстро растут.Например, вы, вероятно, не захотите использовать x = 10 или x = –7 в качестве входных данных. Вы можете выбрать более крупные значения x , если хотите, но ваш график очень быстро станет ужасно высоким.
Из моей Т-диаграммы я вижу, что мои значения и становятся довольно большими на обоих концах (то есть в положительных числах над горизонтальной осью и в отрицательных числах ниже). Я не хочу тратить время на вычисление точек, которые только сделают мой график смехотворно большим, поэтому я уйду с тем, что у меня есть до сих пор. Но я рад, что нарисовал больше, чем две точки, потому что линии, которые начинаются близко к вертикали, могут легко выйти из строя, если я не аккуратен в своей работе.
Но я рад, что нарисовал больше, чем две точки, потому что линии, которые начинаются близко к вертикали, могут легко выйти из строя, если я не аккуратен в своей работе.
Вот мой график:
Я не должен позволять этому уравнению или графику пугать меня. Да, в уравнении нет « x », но это нормально. Я просто думаю об этом так: не имеет значения, какое значение x я выберу; значение y всегда будет 3.
Моя Т-диаграмма может выглядеть примерно так:
Нет, я не собираюсь наносить точку ( x , y ) = (100, 3), но моя T-диаграмма подчеркивает для меня точку. Неважно, какое значение я выберу для x ; значение y равно , всегда будет 3 !.
Это означает, что мой график выглядит так:
Примечание. Каждый раз, когда у вас есть уравнение вида « y равно числу», в котором нет x , на графике всегда будет горизонтальной линией, проходящей через ось y на высоте. какого бы ни было это число.
Каждый раз, когда у вас есть уравнение вида « y равно числу», в котором нет x , на графике всегда будет горизонтальной линией, проходящей через ось y на высоте. какого бы ни было это число.
Я тоже не должен позволять этому пугать меня! Да, в уравнении нет y , поэтому я не могу решить для « y =», но это нормально. Рассуждения работают так же, как и в предыдущем примере. Независимо от того, каким может быть значение y , соответствующее значение x всегда будет 4. (Да, я как бы работаю в обратном направлении, но это нормально. Все, что мне нужно, это точки сюжета. Мне не всегда нужно идти вперед, от значений x до значений y , чтобы получить эти очки.)
Итак, я сделаю свою Т-диаграмму в обратном порядке, выбирая различные значения y , всегда ставя «4» в качестве соответствующих значений x :
Нет, я не собираюсь строить точку ( x , y ) = (4, 100), но эта точка подчеркивает для меня, что для этой линии все значения x будут быть 4, независимо от того, каким могло быть соответствующее значение y . Итак, мой график выглядит так:
Итак, мой график выглядит так:
Примечание. Каждый раз, когда у вас есть уравнение вида « x равно числу», без y в уравнении, на графике всегда будет вертикальной линией, проходящей через ось x при любом это число есть.
Филиал
URL: https: // www.purplemath.com/modules/graphlin3.htm
Узнайте, как изобразить неравенство на числовой прямой
В этом видео мы узнаем, как построить график неравенства без использования графического калькулятора.
Пример отображения неравенств
Здесь мы включаем все числа меньше 5 (слева), но не закрашиваем круг на 5, потому что он не может быть равен 5.
Здесь мы включаем все числа больше 5 (справа), но не закрашиваем кружок на 5, потому что он не может быть равен 5.
Мы включаем все числа меньше 5 (слева), а также закрашиваем круг на 5, потому что он может равняться 5.
Здесь мы включаем все числа больше 5 (справа), а также закрашиваем круг на 5, потому что он может равняться 5.
Стенограмма видеоурока
Давайте рассмотрим, как построить график неравенств.
Прежде всего, что такое неравенство?
Посмотрите на это:
- это уравнение, потому что оно равно определенному числу.
В неравенстве это не совсем равно.
Примеры неравенства:
Или может быть более сложным:
Итак, как изобразить это неравенство?
Давайте посмотрим, как построить уравнение.
Нарисуйте числовую линию. Дело в нашем уравнении.
Теперь посмотрим на неравенство
Здесь у нас есть бесконечное количество решений.Потому что у нас может быть любое число меньше.
Итак, все меньше чем.
Но это так.
Есть бесконечные числа.
Теперь давайте изобразим это.
Нарисуйте числовую линию.
В уравнении есть точка, обозначающая знак равенства.
В неравенстве мы просто обведем конечную точку. В данном случае это. Затем нарисуйте линию, идущую влево, которая представляет бесконечные числа, меньшие чем.
Давайте еще примеры:
Сначала нарисуем числовую прямую.
может быть равно, поэтому мы можем нарисовать на нем точку. Затем проведем линию слева, которая представляет все числа меньше чем.
А теперь поехали.
Нарисуйте числовую линию.
Обведем число и проведем линию вправо, которая представляет все числа больше чем.
Нарисуйте числовую линию.
Выделите номер точки и проведите линию справа, которая представляет все числа больше чем.
Линия под знаком «меньше» или «больше» означает «равно».
имеет то же значение, что и.
Думайте о знаке как о усте. Он будет есть все, что больше.
Аналогичным образом мы можем написать как.
такой же, как.
А также может быть записано как
После того, как вы закончите этот урок, просмотрите все наши уроки алгебры 1 и попрактикуйтесь.
Наибольшая целочисленная функция и график
Краткий обзор
- Функция наибольшего целого числа также известна как функция пола.
- Он записывается как $$ f (x) = \ lfloor x \ rfloor $$.
- Значение $$ \ lfloor x \ rfloor $$ - это наибольшее целое число, которое на меньше или , равное $$ x $$.
Определение
Наибольшая целочисленная функция определяется как
$$ \ lfloor x \ rfloor = \ mbox {наибольшее целое число, которое} $$ меньше или равно $$ x $$.
В математической записи мы бы записали это как
$$
\ lfloor x \ rfloor = \ max \ {m \ in \ mathbb {Z} | m \ leq x \}
$$
Обозначение «$$ m \ in \ mathbb {Z} $$» означает «$$ m $$ - целое число».
Примеры
Пример 1 --- Основные вычисления
Оцените следующее.
- $$ \ пол 2,7 \ пол $
- $$ \ lfloor -1,4 \ rfloor $$
- $$ \ этаж 8 \ этаж $
Решение Если мы рассмотрим числовую строку с целыми числами и 2,7, нанесенными на нее, мы увидим
Наибольшее целое число, которое на меньше 2.7 равно 2. Итак, $$ \ lfloor 2. 7 \ rfloor = 2 $$.
7 \ rfloor = 2 $$.
Если мы рассмотрим числовую строку с целыми числами и нанесенными на нее -1,3, мы увидим
Поскольку наибольшее целое число, которое на меньше -1,3, равно -2, $$ \ lfloor -1,3 \ rfloor = -2 $$.
Поскольку $$ \ lfloor x \ rfloor = $$ наибольшее целое число, которое меньше или равно $$ x $$, мы знаем, что $$ \ lfloor 8 \ rfloor = 8 $$.
Построение графика наибольшей целочисленной функции
Чтобы понять поведение этой функции в терминах графика, давайте построим таблицу значений.
СТОЛ $$
\ begin {array} {| c | c |}
\ hline
x & \ lfloor x \ rfloor \\
\ hline
-1. 5 & -2 \\
-1,25 & -2 \\
-1 & -1 \\
-0,75 & -1 \\
-0,5 & -1 \\
-0,25 и -1 \\
0 & 0 \\
0,25 & 0 \\
0,5 & 0 \\
0,75 & 0 \\
1 и 1 \\
1,25 и 1 \\
1.5 и 1 \\
\ hline
\ end {массив}
$$
5 & -2 \\
-1,25 & -2 \\
-1 & -1 \\
-0,75 & -1 \\
-0,5 & -1 \\
-0,25 и -1 \\
0 & 0 \\
0,25 & 0 \\
0,5 & 0 \\
0,75 & 0 \\
1 и 1 \\
1,25 и 1 \\
1.5 и 1 \\
\ hline
\ end {массив}
$$
Таблица показывает нам, что функция увеличивается до следующего наибольшего целого числа каждый раз, когда значение x становится целым числом. Это приводит к следующему графику.
Отвечать Пример 2
Нарисуйте график $$ y = \ left \ lfloor \ frac 1 2x \ right \ rfloor $$.
Решение Мы знаем, как должен выглядеть основной график, поэтому нам просто нужно понять, как фактор $$ \ frac 1 2 $$ будет влиять на вещи. Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
ТАБЛИЦА
$$
\ begin {align *}
\ begin {array} {| c | c | c |}
\ hline
x & \ frac 1 2 x & \ left \ lfloor \ frac 1 2 x \ right \ rfloor \\ [6pt]
\ hline
-2 и -1.5 & -2 \\ [6pt]
-1,5 и -0,75 и -1 \\ [6pt]
-1 & -0,5 & -1 \\ [6pt]
-0,5 и -0,25 и -1 \\ [6pt]
0 & 0 & 0 \\ [6pt]
0,5 и 0,25 и 0 \\ [6pt]
1 & 0,5 & 0 \\ [6pt]
1,5 и 0,75 и 0 \\ [6pt]
2 и 1 и 1 \\ [6pt]
\ hline
\ end {массив}
\ end {выровнять *}
$$
Мы заметили из таблицы, что значения функции переходят к следующему значению, когда $$ x $$ четно.
ПРЕОБРАЗОВАНИЕ
Мы можем интерпретировать $$ y = \ left \ lfloor \ frac 1 2 x \ right \ rfloor $$ как горизонтальное растяжение, которое удваивает длину каждой части.
Отвечать: Решение уравнений
Существует формула, которая может помочь нам при работе с уравнениями, включающими функцию пола.
$$ \ lfloor x \ rfloor = m \ qquad \ mbox {тогда и только тогда, когда} \ quad m \ leq x
(помните, $$ m $$ - целое число!)
Так, например, $$ \ lfloor x \ rfloor = 8 $$, если и только если $$ 8 \ leq x
Пример 3
Решите уравнение $$ \ lfloor 2x + 5 \ rfloor = 9 $$.
Шаг 1 Перепишем уравнение, используя неравенство.
$$ 9 \ leq 2x + 5
Шаг 2
Решите неравенство.
$$
\ begin {align *}
9 & \ leq 2x + 5 Отвечать:
В интервальной записи уравнение верно для $$ x \ в [2, 2.5) $$.
Пример 4
Решите уравнение $$ \ lfloor 1.25 + \ lfloor x \ rfloor \ rfloor = 12 $$.
Шаг 1 Замените $$ \ lfloor x \ rfloor $$ на $$ u $$. Это называется «заменой переменной», и это облегчает работу с уравнением.
$$
\ begin {align *}
\ lfloor 1.25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$
Шаг 2 Заменить уравнение одним из неравенств, где $$ m = 12 $$
$$
12 \ leq 1. 25 + u Шаг 3
25 + u Шаг 3 Решите неравенство.
$$
\ begin {align *}
12 & \ leq 1.25 + ю
Поскольку $$ \ lfloor x \ rfloor $$ является целым числом, единственный способ удовлетворить указанные выше неравенства - это $$ \ lfloor x \ rfloor = 11 $$.
Шаг 4 Определите значение $$ x $$.
Опять же, используя неравенства, мы знаем
$$
11 \ leq x Отвечать:
$$
11 \ leq x
Продолжайте практиковать проблемы Ошибка: Нажмите «Не робот», затем повторите попытку.
графов линейных неравенств - элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Проверить решения неравенства по двум переменным
- Распознавать связь между решениями неравенства и его графиком
- График линейных неравенств
Проверка решения неравенства по двум переменным
Мы научились решать неравенства по одной переменной. Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
Линейное неравенство
Линейное неравенство - это неравенство, которое можно записать в одной из следующих форм:
, где оба не равны нулю.
Вы помните, что у неравенства с одной переменной было много решений? Решение неравенства - любое число больше 3.Мы показали это на числовой строке, закрасив числовую строку справа от 3 и поставив открывающую скобку на 3. См. (Рисунок).
Точно так же неравенства с двумя переменными имеют много решений. Любая упорядоченная пара, которая делает неравенство истинным, когда мы подставляем значения, является решением неравенства.
Решение линейного неравенства
Упорядоченная пара является решением линейного неравенства, если неравенство истинно, когда мы подставляем значения x и y .
Решение
- ⓐ
- ⓑ
- ⓒ
- ⓓ
- ⓔ
ⓐ да ⓑ да ⓒ да ⓓ да ⓔ нет
ⓐ да ⓑ да ⓒ нет ⓓ нет ⓔ да
Распознать связь между решениями неравенства и его графиком
Теперь посмотрим, как решения неравенства соотносятся с его графом.
Давайте снова подумаем о числовой прямой на (Рисунок).Точка разделяла эту числовую линию на две части. С одной стороны от 3 все числа меньше 3. С другой стороны от 3 все числа больше 3. См. (Рисунок).
Решение для - это заштрихованная часть числовой прямой справа от.
Точно так же линия разделяет плоскость на две области. По одну сторону от линии есть точки с. На другой стороне линии находятся точки с. Мы называем линию границей.
Граница
Линия с уравнением - это граница, отделяющая область where от области where.
Для неравенства в одной переменной конечная точка отображается в круглых скобках или скобках в зависимости от того, включено ли в решение или нет:
Аналогичным образом, для неравенства двух переменных граничная линия показана сплошной или пунктирной линией, чтобы указать, включена ли эта линия в решение. Это кратко показано на (Рисунок)
Это кратко показано на (Рисунок)
. Граничная линия не включена в решение.
Граничная линия включена в решение. Граничная линия пунктирная. Граничная линия сплошная.
Теперь давайте посмотрим на то, что мы обнаружили на (Рисунок). Мы начнем с построения линии, а затем нанесем пять протестированных точек. См. (Рисунок).
В (рисунок) мы обнаружили, что некоторые из пунктов были решениями неравенства, а некоторые - нет.
Какие из нанесенных нами точек являются решениями неравенства? Точки и являются решениями неравенства.Обратите внимание, что они оба находятся по одну сторону от граничной линии.
Две точки и находятся по другую сторону от граничной линии, и они не являются решениями неравенства. По этим двум точкам.
В чем суть? Потому что точка - это решение уравнения. Итак, точка находится на границе.
Итак, точка находится на границе.
Давайте возьмем другую точку слева от граничной линии и проверим, является ли она решением неравенства. Точка явно выглядит слева от ограничивающей линии, не так ли? Это решение неравенства?
Любая точка, которую вы выбираете слева от граничной линии, является решением неравенства.Все точки слева - решения.
Аналогично, все точки на правой стороне граничной линии, на стороне с и, не являются решениями. См. (Рисунок).
График неравенства показан на (Рисунок) ниже. Линия делит плоскость на две области. Затененной стороной показаны решения неравенства.
Точки на граничной линии (те, где) не являются решениями неравенства, поэтому сама линия не является частью решения. Мы показываем это, делая линию пунктирной, а не сплошной.
График неравенства. Показана граничная линия. Напишите неравенство, показанное на графике.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное на графике с линией границы.
Показана граничная линия. Напишите неравенство, показанное на графике.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Упражнения по разделам
Письменные упражнения
Лестер считает, что решение любого неравенства со знаком> - это область над линией, а решение любого неравенства со знаком <- это область ниже линии. Лестер прав? Объясните, почему да или почему нет.
Объясните, почему на некоторых графиках линейных неравенств граничная линия сплошная, а на других - пунктирная.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глава 4 Упражнения на повторение
Прямоугольная система координат
Точки графика в прямоугольной системе координат
В следующих упражнениях нанесите каждую точку в прямоугольную систему координат.
Определить точки на графике
В следующих упражнениях назовите упорядоченную пару каждой точки, показанной в прямоугольной системе координат.
Проверка решения уравнения с двумя переменными
Какие упорядоченные пары являются решениями данных уравнений в следующих упражнениях?
Заполните таблицу решений линейного уравнения с двумя переменными
В следующих упражнениях заполните таблицу, чтобы найти решения каждого линейного уравнения.
Найти решения линейного уравнения с двумя переменными
В следующих упражнениях найдите три решения каждого линейного уравнения.
Построение графиков линейных уравнений
Распознать связь между решениями уравнения и его графика
В следующих упражнениях для каждой упорядоченной пары определите:
- ⓐ Является ли упорядоченная пара решением уравнения?
- ⓑ Это точка на линии?
ⓐ да; да ⓑ да; нет
Построение линейного уравнения по точкам
В следующих упражнениях построите график путем нанесения точек.
График Вертикальные и горизонтальные линии
В следующих упражнениях нанесите на график каждое уравнение.
В следующих упражнениях нарисуйте каждую пару уравнений в одной прямоугольной системе координат.
и
Графики с перехватами
Определите точки пересечения x и y на графике
В следующих упражнениях найдите точки перехвата x и y .
Найдите точки пересечения x и y из уравнения прямой
В следующих упражнениях найдите точки пересечения каждого уравнения.
Построение линии с помощью точек пересечения
В следующих упражнениях построите график с использованием точек пересечения.
Уклон прямой
Использование географических досок для моделирования уклона
В следующих упражнениях найдите уклон, смоделированный на каждой геодлане.
В следующих упражнениях моделируйте каждый уклон. Нарисуйте картинку, чтобы показать свои результаты.
Используйте, чтобы найти наклон прямой из графика
В следующих упражнениях найдите наклон каждой показанной линии.
Найдите наклон горизонтальной и вертикальной линий
В следующих упражнениях найдите наклон каждой линии.
Используйте формулу наклона, чтобы найти наклон линии между двумя точками
В следующих упражнениях используйте формулу наклона, чтобы найти наклон линии между каждой парой точек.
Построение линии через точку и наклон
В следующих упражнениях нарисуйте каждую линию с заданной точкой и наклоном.
;
x - перехват;
y -перехват 1;
Решите наклонные приложения
В следующих упражнениях решите эти приложения для уклонов.
Крыша, изображенная ниже, имеет высоту 10 футов и высоту 15 футов. Какой у него наклон?
Горная дорога поднимается на 50 футов для бега на 500 футов. Какой у него наклон?
Форма перехвата уравнения прямой
Распознать связь между графиком и формой наклона-пересечения уравнения прямой
В следующих упражнениях используйте график, чтобы найти наклон и пересечение y каждой линии. Сравните значения с уравнением.
Сравните значения с уравнением.
Определите наклон и точку пересечения оси y из уравнения линии
В следующих упражнениях определите наклон и пересечение y каждой линии.
Построение линии по ее наклону и пересечению
В следующих упражнениях нарисуйте линию каждого уравнения, используя ее наклон и точку пересечения y .
В следующих упражнениях определите наиболее удобный метод построения графика каждой линии.
График и интерпретация значений наклона и пересечения
Кэтрин - частный повар. Уравнение моделирует связь между ее недельными затратами, C , в долларах, и количеством приемов пищи, м , которые она обслуживает.
- ⓐ Найдите стоимость Кэтрин за неделю, когда она не обслуживает гостей.
- ⓑ Узнайте стоимость недели, когда она готовит 14 блюд.
- ⓒ Интерпретировать наклон и пересечение C уравнения.
- ⓓ Изобразите уравнение.
Марджори преподает фортепиано. Уравнение моделирует связь между ее еженедельной прибылью P в долларах и количеством уроков, которые она преподает студентам, s .
- ⓐ Найдите прибыль Марджори за неделю, когда она не учит студентов.
- ⓑ Получите прибыль за неделю, когда она проведет 20 уроков для студентов.
- ⓒ Интерпретируйте наклон и P - точку пересечения уравнения.
- ⓓ Изобразите уравнение.
ⓐ - 250 ⓑ 450 ⓒ Наклон 35 означает, что еженедельная прибыль Марджори, P , увеличивается на 35 фунтов стерлингов за каждый дополнительный урок учащегося, который она преподает. Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ
Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ
Использование уклонов для определения параллельных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, параллельны ли линии.
Используйте уклоны для определения перпендикулярных линий
В следующих упражнениях используйте наклоны и точки пересечения по оси Y, чтобы определить, перпендикулярны ли линии.
Найдите уравнение прямой
Найдите уравнение прямой с учетом наклона и пересечения y -пересечение
В следующих упражнениях найдите уравнение прямой с заданным наклоном и точкой пересечения по оси Y.Запишите уравнение в форме угла наклона и точки пересечения.
В следующих упражнениях найдите уравнение линии, показанной на каждом графике. Запишите уравнение в форме угла наклона и точки пересечения.
Найдите уравнение прямой с учетом наклона и точки
В следующих упражнениях найдите уравнение прямой с заданным наклоном, содержащей заданную точку. Запишите уравнение в форме угла наклона и точки пересечения.
, пункт
Горизонтальная строка, содержащая
Найти уравнение прямой по двум точкам
В следующих упражнениях найдите уравнение прямой, содержащей заданные точки. Запишите уравнение в форме угла наклона и точки пересечения.
и
и.
Найдите уравнение прямой, параллельной заданной
В следующих упражнениях найдите уравнение прямой, параллельной данной прямой и содержащей данную точку. Запишите уравнение в форме угла наклона и точки пересечения.
Запишите уравнение в форме угла наклона и точки пересечения.
линия, точка
линия, точка
Найдите уравнение прямой, перпендикулярной заданной
В следующих упражнениях найдите уравнение прямой, перпендикулярной данной прямой и содержащей данную точку. Запишите уравнение в форме угла наклона и точки пересечения.
линия, точка
линия, точка
График линейных неравенств
Проверка решения неравенства по двум переменным
В следующих упражнениях определите, является ли каждая упорядоченная пара решением данного неравенства.
ⓐ да ⓑ нет ⓒ да ⓓ да ⓔ нет
Распознать связь между решениями неравенства и его графиком
В следующих упражнениях запишите неравенство, показанное заштрихованной областью.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
Запишите неравенство, показанное заштрихованной областью на графике с линией границы.
График линейных неравенств
В следующих упражнениях нанесите на график каждое линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Изобразите линейное неравенство.
Напишите уравнение для линейной функции из графика линии
Напомним, что в разделе «Линейные функции» мы написали уравнение для линейной функции из графика. Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начнем с просмотра рисунка 8. Сразу видно, что график пересекает ось y в точке (0, 4), так что это пересечение y .
Начнем с просмотра рисунка 8. Сразу видно, что график пересекает ось y в точке (0, 4), так что это пересечение y .
Рисунок 8
Затем мы можем рассчитать наклон, найдя подъем и пробег. Мы можем выбрать любые две точки, но давайте посмотрим на точку (–2, 0). Чтобы добраться из этой точки до точки пересечения y- , мы должны переместиться на 4 единицы вверх (подъем) и на 2 единицы вправо (бег). Значит, уклон должен быть
[латекс] m = \ frac {\ text {rise}} {\ text {run}} = \ frac {4} {2} = 2 [/ latex]
Подставляя наклон и точку пересечения y- в форму линии пересечения наклона, получаем
[латекс] y = 2x + 4 [/ латекс]
Практическое руководство. Имея график линейной функции, найдите уравнение для описания функции.
- Определите точку пересечения y- уравнения.

- Выберите две точки для определения наклона.
- Замените точку пересечения y- и уклон в форму линии пересечения с уклоном.
Пример 4: Сопоставление линейных функций с их графиками
Сопоставьте каждое уравнение линейных функций с одной из линий на рисунке 9.
- [латекс] f \ left (x \ right) = 2x + 3 [/ латекс]
- [латекс] g \ left (x \ right) = 2x - 3 [/ латекс]
- [латекс] h \ left (x \ right) = - 2x + 3 [/ латекс]
- [латекс] j \ left (x \ right) = \ frac {1} {2} x + 3 [/ latex]
Рисунок 9
Решение
Проанализируйте информацию по каждой функции.
- Эта функция имеет наклон 2 и пересечение y - 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или можем сравнить его с другими перечисленными функциями.
 Функция g имеет тот же наклон, но другую точку пересечения y- . Линии I и III имеют одинаковый уклон, потому что они имеют одинаковый уклон. Линия III не проходит через (0, 3), поэтому f должен быть представлен линией I.
Функция g имеет тот же наклон, но другую точку пересечения y- . Линии I и III имеют одинаковый уклон, потому что они имеют одинаковый уклон. Линия III не проходит через (0, 3), поэтому f должен быть представлен линией I. - Эта функция также имеет наклон 2, но пересечение y –3. Он должен проходить через точку (0, –3) и наклоняться вверх слева направо. Он должен быть представлен линией III.
- Эта функция имеет наклон –2 и точку пересечения y- , равную 3. Это единственная перечисленная функция с отрицательным наклоном, поэтому она должна быть представлена линией IV, поскольку она наклонена вниз слева направо.
- Эта функция имеет наклон [latex] \ frac {1} {2} [/ latex] и точку пересечения y- равную 3.Он должен проходить через точку (0, 3) и наклоняться вверх слева направо. Линии I и II проходят через (0, 3), но наклон j меньше, чем наклон f , поэтому линия j должна быть более пологой.
 Эта функция представлена линией II.
Эта функция представлена линией II.
Теперь мы можем перемаркировать линии, как на рисунке 10.
Рисунок 10
Нахождение перехвата x линии
До сих пор мы находили точки пересечения y- функции: точку, в которой график функции пересекает ось y .Функция также может иметь точку пересечения x , , которая является координатой x точки, в которой график функции пересекает ось x . Другими словами, это входное значение, когда выходное значение равно нулю.
Чтобы найти точку пересечения x , установите функцию f ( x ) равной нулю и найдите значение x . Например, рассмотрим показанную функцию.
[латекс] f \ left (x \ right) = 3x - 6 [/ латекс]
Задайте для функции значение 0 и найдите x .
[латекс] \ begin {case} 0 = 3x - 6 \ hfill \\ 6 = 3x \ hfill \\ 2 = x \ hfill \\ x = 2 \ hfill \ end {case} [/ latex]
График функции пересекает ось x в точке (2, 0).
Вопросы и ответы
Все ли линейные функции имеют точки пересечения x ?
Нет. Однако линейные функции вида y = c , где c - ненулевое действительное число, являются единственными примерами линейных функций без интерцепта x .Например, y = 5 - это горизонтальная линия на 5 единиц выше оси x . Эта функция не имеет x - перехватывает .
Рисунок 11
A Общее примечание:
x - перехват Перехват x функции - это значение x , когда f ( x ) = 0. Его можно решить уравнением 0 = mx + b .
Его можно решить уравнением 0 = mx + b .
Пример 5: Нахождение перехвата
x Найдите точку пересечения x [латекс] f \ left (x \ right) = \ frac {1} {2} x - 3 [/ latex].
Решение
Установите функцию равной нулю, чтобы найти x .
[латекс] \ begin {case} 0 = \ frac {1} {2} x - 3 \\ 3 = \ frac {1} {2} x \\ 6 = x \\ x = 6 \ end {case} [/ латекс]
График пересекает ось x в точке (6, 0).
Рисунок 12. График линейной функции [латекс] f \ left (x \ right) = \ frac {1} {2} x - 3 [/ latex].
Попробовать 4
Найдите точку пересечения x [латекс] f \ left (x \ right) = \ frac {1} {4} x - 4 [/ latex].
Решение
Описание горизонтальных и вертикальных линий
Есть два особых случая линий на графике - горизонтальные и вертикальные линии. Горизонтальная линия указывает на постоянный выход или значение y . На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение выходных сигналов между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m = 0 в уравнении [латекс] f \ left (x \ right) = mx + b [/ latex], уравнение упрощается до [latex] f \ left (x \ right) = b [/ latex].Другими словами, значение функции постоянно. Этот график представляет функцию [латекс] f \ left (x \ right) = 2 [/ latex].
Горизонтальная линия указывает на постоянный выход или значение y . На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение выходных сигналов между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m = 0 в уравнении [латекс] f \ left (x \ right) = mx + b [/ latex], уравнение упрощается до [latex] f \ left (x \ right) = b [/ latex].Другими словами, значение функции постоянно. Этот график представляет функцию [латекс] f \ left (x \ right) = 2 [/ latex].
Рис. 13. Горизонтальная линия, представляющая функцию [латекс] f \ left (x \ right) = 2 [/ latex].
Рисунок 14
Вертикальная линия указывает постоянный ввод или значение x . Мы видим, что входное значение для каждой точки на линии равно 2, но выходное значение меняется. Поскольку это входное значение отображается более чем на одно выходное значение, вертикальная линия не представляет функцию.Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.
Поскольку это входное значение отображается более чем на одно выходное значение, вертикальная линия не представляет функцию.Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.
Обратите внимание, что вертикальная линия, такая как линия на рис. 15 , , имеет точку пересечения x , но не имеет точки пересечения y- , если только это не линия x = 0. Этот график представляет линию x = 2.
Рисунок 15. Вертикальная линия x = 2, которая не представляет функцию.
Общее примечание: горизонтальные и вертикальные линии
Линии могут быть горизонтальными или вертикальными.
Горизонтальная линия - это линия, определяемая уравнением в форме [латекс] f \ left (x \ right) = b [/ latex].
Вертикальная линия - это линия, определяемая уравнением в форме [латекс] x = a [/ latex].
Пример 6: Написание уравнения горизонтальной линии
Напишите уравнение линии, изображенной на рисунке 16.
Рисунок 16
Решение
Для любого значения x значение y равно –4, поэтому уравнение: y = –4.
Пример 7: Написание уравнения вертикальной прямой
Напишите уравнение линии, показанной на рисунке 17.
Рисунок 17
Решение
Константа x - значение 7, поэтому уравнение x = 7.
Графическое изображение линейных неравенств
Это график линейного неравенства:
Неравенство y ≤ x + 2
Вы можете увидеть линию y = x + 2, а заштрихованная область - это место, где y меньше или равно x + 2
Линейное неравенство
Линейное неравенство похоже на линейное уравнение (например, y = 2x + 1 ). ..
..
... но у него будет Неравенство вроде <,>, ≤ или ≥ вместо = .
Как построить график линейного неравенства
Сначала нарисуйте линию «равно», затем заштрихуйте нужную область.
Есть три шага:
- Переставьте уравнение так, чтобы «y» находилось слева, а все остальное - справа.
- Постройте линию « y = » (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y < или y> )
- Затенение над линией для «больше чем» ( y> или y≥ )
или ниже линии для «меньше чем» ( y < или y≤ ).
Попробуем несколько примеров:
Пример: y≤2x-1
1. Неравенство уже имеет "y" слева и все остальное справа, поэтому нет необходимости переставлять
2. График y = 2x-1 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: 2y - x ≤ 6
1. Нам нужно будет переставить это так, чтобы "y" находилось слева само по себе:
Нам нужно будет переставить это так, чтобы "y" находилось слева само по себе:
Начать с: 2y - x ≤ 6
Добавьте x к обеим сторонам: 2y ≤ x + 6
Разделить все на 2: y ≤ x / 2 + 3
2. Теперь постройте y = x / 2 + 3 (сплошная линия, потому что y≤ включает , равное )
3. Закрасьте область ниже (поскольку y на меньше или равно)
Пример: y / 2 + 2> x
1.Нам нужно будет переставить это так, чтобы "y" находилось слева само по себе:
Начать с: y / 2 + 2> x
Вычтем 2 с обеих сторон: y / 2> x - 2
Умножить все на 2: y> 2x - 4
2. Теперь постройте y = 2x - 4 (пунктирная линия, потому что y> не включает равно)
3. Закрасьте область выше (поскольку y на больше )
Пунктирная линия показывает, что неравенство не включает линию y = 2x-4 .
Два особых случая
У вас также может быть горизонтальная или вертикальная линия:
Здесь показано, где y меньше 4
(от линии y = 4 вниз, но не включая ее)
Обратите внимание, что у нас есть пунктирная линия, чтобы показать, что она не включает где y = 4 В этом даже нет y!
Он имеет линию x = 1 и закрашен для всех значений x, больших (или равных) 1
.
 factor(partner))
trades # посмотрим, что получилось
## # A tibble: 720 x 5
## sitc06 partner time export import
## <chr> <fct> <date> <dbl> <dbl>
## 1 Food, drinks and tobacco Argentina 2008-01-01 81.3 7334
## 2 Food, drinks and tobacco Brazil 2008-01-01 600. 9639.
## 3 Food, drinks and tobacco Canada 2008-01-01 1950. 1458.
## 4 Food, drinks and tobacco Switzerland 2008-01-01 5000. 2727.
## 5 Food, drinks and tobacco China except Hong Kong 2008-01-01 1322. 3567.
## 6 Food, drinks and tobacco Japan 2008-01-01 3964. 119.
## 7 Food, drinks and tobacco Norway 2008-01-01 2416. 3012.
## 8 Food, drinks and tobacco Russia 2008-01-01 7567. 855.
## 9 Food, drinks and tobacco Turkey 2008-01-01 1175 3160.
## 10 Food, drinks and tobacco United States 2008-01-01 10021.
factor(partner))
trades # посмотрим, что получилось
## # A tibble: 720 x 5
## sitc06 partner time export import
## <chr> <fct> <date> <dbl> <dbl>
## 1 Food, drinks and tobacco Argentina 2008-01-01 81.3 7334
## 2 Food, drinks and tobacco Brazil 2008-01-01 600. 9639.
## 3 Food, drinks and tobacco Canada 2008-01-01 1950. 1458.
## 4 Food, drinks and tobacco Switzerland 2008-01-01 5000. 2727.
## 5 Food, drinks and tobacco China except Hong Kong 2008-01-01 1322. 3567.
## 6 Food, drinks and tobacco Japan 2008-01-01 3964. 119.
## 7 Food, drinks and tobacco Norway 2008-01-01 2416. 3012.
## 8 Food, drinks and tobacco Russia 2008-01-01 7567. 855.
## 9 Food, drinks and tobacco Turkey 2008-01-01 1175 3160.
## 10 Food, drinks and tobacco United States 2008-01-01 10021. \circ\) Выгрузим данные по температуре, относительной влажности и осадкам в Екатеринбурге (\(60.59~в.д.\), \(56.84~с.ш.\)) за период с 1 по 30 апреля 1995 года:
\circ\) Выгрузим данные по температуре, относительной влажности и осадкам в Екатеринбурге (\(60.59~в.д.\), \(56.84~с.ш.\)) за период с 1 по 30 апреля 1995 года:
 2/day)
##
## # A tibble: 4 x 17
## LON LAT PARAMETER YEAR JAN FEB MAR APR MAY JUN JUL AUG
## <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 60.6 56.8 CLRSKY_S… 1995 0.91 2.07 3.93 5.93 7.27 7.98 7.54 6.13
## 2 60.6 56.8 CLRSKY_S… 1996 0.94 2.12 4.02 6.24 7.37 7.93 7.42 6.23
## 3 60.6 56.8 ALLSKY_S… 1995 0.68 1.41 2.8 4.75 5.42 6.04 5.78 4.13
## 4 60.6 56.8 ALLSKY_S… 1996 0.76 1.57 3.39 4.82 5.3 6.2 5.58 4.5
## # … with 5 more variables: SEP <dbl>, OCT <dbl>, NOV <dbl>, DEC <dbl>,
## # ANN <dbl>
2/day)
##
## # A tibble: 4 x 17
## LON LAT PARAMETER YEAR JAN FEB MAR APR MAY JUN JUL AUG
## <dbl> <dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 60.6 56.8 CLRSKY_S… 1995 0.91 2.07 3.93 5.93 7.27 7.98 7.54 6.13
## 2 60.6 56.8 CLRSKY_S… 1996 0.94 2.12 4.02 6.24 7.37 7.93 7.42 6.23
## 3 60.6 56.8 ALLSKY_S… 1995 0.68 1.41 2.8 4.75 5.42 6.04 5.78 4.13
## 4 60.6 56.8 ALLSKY_S… 1996 0.76 1.57 3.39 4.82 5.3 6.2 5.58 4.5
## # … with 5 more variables: SEP <dbl>, OCT <dbl>, NOV <dbl>, DEC <dbl>,
## # ANN <dbl> Как правило, серии именуются по названию населенного пункта, рядом с которым впервые были найдены подобные почвы.
Как правило, серии именуются по названию населенного пункта, рядом с которым впервые были найдены подобные почвы. frame"
## .. .. ..$ aqp_group_by : chr ""
## .. .. ..$ aqp_hzdesgn : chr "hzname"
## .. .. ..$ aqp_hztexcl : chr "texture_class"
## .. .. ..$ depth_units : chr "cm"
## .. .. ..$ stringsAsFactors: logi FALSE
## .. .. ..$ original.order : int [1:22] 1 2 3 4 5 6 7 8 9 10 ...
## .. .. ..$ origin : chr "OSD via Soilweb / fetchOSD"
## .. ..@ horizons :'data.frame': 22 obs. of 19 variables:
## .. .. ..$ id : chr [1:22] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## .. .. ..$ top : int [1:22] 0 10 36 66 97 119 152 0 20 46 ...
## .. .. ..$ bottom : int [1:22] 10 36 66 97 119 152 203 20 46 56 ...
## .. .. ..$ hzname : chr [1:22] "Ap" "Bw1" "Bw2" "Bw3" ...
## .. .. ..$ soil_color : chr [1:22] "#7E5A3BFF" "#7A5C37FF" "#7A5C37FF" "#7E5A3BFF" ...
## .. .. ..$ hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ value : int [1:22] 4 4 4 4 5 5 4 4 4 3 ...
## .. .. ..$ chroma : int [1:22] 4 4 4 4 8 1 4 4 3 3 .
frame"
## .. .. ..$ aqp_group_by : chr ""
## .. .. ..$ aqp_hzdesgn : chr "hzname"
## .. .. ..$ aqp_hztexcl : chr "texture_class"
## .. .. ..$ depth_units : chr "cm"
## .. .. ..$ stringsAsFactors: logi FALSE
## .. .. ..$ original.order : int [1:22] 1 2 3 4 5 6 7 8 9 10 ...
## .. .. ..$ origin : chr "OSD via Soilweb / fetchOSD"
## .. ..@ horizons :'data.frame': 22 obs. of 19 variables:
## .. .. ..$ id : chr [1:22] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## .. .. ..$ top : int [1:22] 0 10 36 66 97 119 152 0 20 46 ...
## .. .. ..$ bottom : int [1:22] 10 36 66 97 119 152 203 20 46 56 ...
## .. .. ..$ hzname : chr [1:22] "Ap" "Bw1" "Bw2" "Bw3" ...
## .. .. ..$ soil_color : chr [1:22] "#7E5A3BFF" "#7A5C37FF" "#7A5C37FF" "#7E5A3BFF" ...
## .. .. ..$ hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ value : int [1:22] 4 4 4 4 5 5 4 4 4 3 ...
## .. .. ..$ chroma : int [1:22] 4 4 4 4 8 1 4 4 3 3 . ..
## .. .. ..$ dry_hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ dry_value : int [1:22] 6 6 6 6 6 6 6 6 6 5 ...
## .. .. ..$ dry_chroma : int [1:22] 4 4 4 4 7 1 4 4 3 3 ...
## .. .. ..$ texture_class: Ord.factor w/ 21 levels "coarse sand"<..: 13 18 17 13 17 17 13 13 13 NA ...
## .. .. ..$ cf_class : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH_class : Ord.factor w/ 12 levels "ultra acid"<"extremely acid"<..: 3 3 3 3 3 3 3 4 NA NA ...
## .. .. ..$ distinctness : chr [1:22] "clear" "gradual" "gradual" "gradual" ...
## .. .. ..$ topography : chr [1:22] "smooth" "wavy" "wavy" "wavy" ...
## .. .. ..$ narrative : chr [1:22] "Ap--0 to 4 inches; brown (7.5YR 4/4) loam; weak medium granular structure; friable; common very fine, fine, and"| __truncated__ "Bw1--4 to 14 inches; dark yellowish brown (10YR 4/4) silty clay loam; weak medium subangular blocky structure; "| __truncated__ "Bw2--14 to 26 inches; dark yellowish brown (10YR 4/4) clay loam; weak medium subangular blocky structure; friab"| __truncated__ "Bw3--26 to 38 inches; brown (7.
..
## .. .. ..$ dry_hue : chr [1:22] "7.5YR" "10YR" "10YR" "7.5YR" ...
## .. .. ..$ dry_value : int [1:22] 6 6 6 6 6 6 6 6 6 5 ...
## .. .. ..$ dry_chroma : int [1:22] 4 4 4 4 7 1 4 4 3 3 ...
## .. .. ..$ texture_class: Ord.factor w/ 21 levels "coarse sand"<..: 13 18 17 13 17 17 13 13 13 NA ...
## .. .. ..$ cf_class : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH : logi [1:22] NA NA NA NA NA NA ...
## .. .. ..$ pH_class : Ord.factor w/ 12 levels "ultra acid"<"extremely acid"<..: 3 3 3 3 3 3 3 4 NA NA ...
## .. .. ..$ distinctness : chr [1:22] "clear" "gradual" "gradual" "gradual" ...
## .. .. ..$ topography : chr [1:22] "smooth" "wavy" "wavy" "wavy" ...
## .. .. ..$ narrative : chr [1:22] "Ap--0 to 4 inches; brown (7.5YR 4/4) loam; weak medium granular structure; friable; common very fine, fine, and"| __truncated__ "Bw1--4 to 14 inches; dark yellowish brown (10YR 4/4) silty clay loam; weak medium subangular blocky structure; "| __truncated__ "Bw2--14 to 26 inches; dark yellowish brown (10YR 4/4) clay loam; weak medium subangular blocky structure; friab"| __truncated__ "Bw3--26 to 38 inches; brown (7. 5YR 4/4) loam; weak medium subangular blocky structure; friable; common fine roo"| __truncated__ ...
## .. .. ..$ hzID : chr [1:22] "1" "2" "3" "4" ...
## .. ..@ site :'data.frame': 3 obs. of 33 variables:
## .. .. ..$ id : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## .. .. ..$ soiltaxclasslastupdated: chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "1997-06-06 00:00:00+00"
## .. .. ..$ mlraoffice : int [1:3] 3 3 3
## .. .. ..$ series_status : chr [1:3] "established" "established" "established"
## .. .. ..$ family : chr [1:3] "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" "fine-loamy, mixed, active, nonacid, thermic oxyaquic udifluvents" "loamy, mixed, active, thermic, shallow typic hapludalfs"
## .. .. ..$ soilorder : chr [1:3] "inceptisols" "entisols" "alfisols"
## .. .. ..$ suborder : chr [1:3] "udepts" "fluvents" "udalfs"
## .. .. ..$ greatgroup : chr [1:3] "dystrudepts" "udifluvents" "hapludalfs"
## .
5YR 4/4) loam; weak medium subangular blocky structure; friable; common fine roo"| __truncated__ ...
## .. .. ..$ hzID : chr [1:22] "1" "2" "3" "4" ...
## .. ..@ site :'data.frame': 3 obs. of 33 variables:
## .. .. ..$ id : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## .. .. ..$ soiltaxclasslastupdated: chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "1997-06-06 00:00:00+00"
## .. .. ..$ mlraoffice : int [1:3] 3 3 3
## .. .. ..$ series_status : chr [1:3] "established" "established" "established"
## .. .. ..$ family : chr [1:3] "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts" "fine-loamy, mixed, active, nonacid, thermic oxyaquic udifluvents" "loamy, mixed, active, thermic, shallow typic hapludalfs"
## .. .. ..$ soilorder : chr [1:3] "inceptisols" "entisols" "alfisols"
## .. .. ..$ suborder : chr [1:3] "udepts" "fluvents" "udalfs"
## .. .. ..$ greatgroup : chr [1:3] "dystrudepts" "udifluvents" "hapludalfs"
## . . .. ..$ subgroup : chr [1:3] "fluvaquentic dystrudepts" "oxyaquic udifluvents" "typic hapludalfs"
## .. .. ..$ tax_partsize : chr [1:3] "fine-loamy" "fine-loamy" "loamy"
## .. .. ..$ tax_partsizemod : logi [1:3] NA NA NA
## .. .. ..$ tax_ceactcl : chr [1:3] "active" "active" "active"
## .. .. ..$ tax_reaction : chr [1:3] NA "nonacid" NA
## .. .. ..$ tax_tempcl : chr [1:3] "thermic" "thermic" "thermic"
## .. .. ..$ originyear : logi [1:3] NA NA NA
## .. .. ..$ establishedyear : int [1:3] 1937 1904 1916
## .. .. ..$ descriptiondateinitial : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ descriptiondateupdated : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ benchmarksoilflag : int [1:3] 1 0 0
## .. .. ..$ statsgoflag : int [1:3] 1 1 1
## .. .. ..$ objwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .
. .. ..$ subgroup : chr [1:3] "fluvaquentic dystrudepts" "oxyaquic udifluvents" "typic hapludalfs"
## .. .. ..$ tax_partsize : chr [1:3] "fine-loamy" "fine-loamy" "loamy"
## .. .. ..$ tax_partsizemod : logi [1:3] NA NA NA
## .. .. ..$ tax_ceactcl : chr [1:3] "active" "active" "active"
## .. .. ..$ tax_reaction : chr [1:3] NA "nonacid" NA
## .. .. ..$ tax_tempcl : chr [1:3] "thermic" "thermic" "thermic"
## .. .. ..$ originyear : logi [1:3] NA NA NA
## .. .. ..$ establishedyear : int [1:3] 1937 1904 1916
## .. .. ..$ descriptiondateinitial : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ descriptiondateupdated : chr [1:3] "2010-02-11 00:00:00+00" "2002-07-18 00:00:00+00" "2007-09-06 00:00:00+00"
## .. .. ..$ benchmarksoilflag : int [1:3] 1 0 0
## .. .. ..$ statsgoflag : int [1:3] 1 1 1
## .. .. ..$ objwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## . . .. ..$ recwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .. .. ..$ typelocstareaiidref : int [1:3] 6691 6706 6691
## .. .. ..$ typelocstareatypeiidref: int [1:3] 3 3 3
## .. .. ..$ soilseriesiid : int [1:3] 24628 1057 23800
## .. .. ..$ soilseriesdbiidref : int [1:3] 122 122 122
## .. .. ..$ grpiidref : int [1:3] 15801 15801 15801
## .. .. ..$ tax_minclass : chr [1:3] "mixed" "mixed" "mixed"
## .. .. ..$ subgroup_mod : chr [1:3] "fluvaquentic" "oxyaquic" "typic"
## .. .. ..$ greatgroup_mod : chr [1:3] "dystr" "udi" "hapl"
## .. .. ..$ drainagecl : chr [1:3] "somewhat poorly" "well" "well"
## .. .. ..$ ac : int [1:3] 1259224 216875 617848
## .. .. ..$ n_polygons : int [1:3] 40647 10387 34748
## .. ..@ sp :Formal class 'SpatialPoints' [package "sp"] with 3 slots
## .. .. .. ..@ coords : num [1, 1] 0
## .
. .. ..$ recwlupdated : chr [1:3] "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00" "2012-08-01 14:06:37+00"
## .. .. ..$ typelocstareaiidref : int [1:3] 6691 6706 6691
## .. .. ..$ typelocstareatypeiidref: int [1:3] 3 3 3
## .. .. ..$ soilseriesiid : int [1:3] 24628 1057 23800
## .. .. ..$ soilseriesdbiidref : int [1:3] 122 122 122
## .. .. ..$ grpiidref : int [1:3] 15801 15801 15801
## .. .. ..$ tax_minclass : chr [1:3] "mixed" "mixed" "mixed"
## .. .. ..$ subgroup_mod : chr [1:3] "fluvaquentic" "oxyaquic" "typic"
## .. .. ..$ greatgroup_mod : chr [1:3] "dystr" "udi" "hapl"
## .. .. ..$ drainagecl : chr [1:3] "somewhat poorly" "well" "well"
## .. .. ..$ ac : int [1:3] 1259224 216875 617848
## .. .. ..$ n_polygons : int [1:3] 40647 10387 34748
## .. ..@ sp :Formal class 'SpatialPoints' [package "sp"] with 3 slots
## .. .. .. ..@ coords : num [1, 1] 0
## .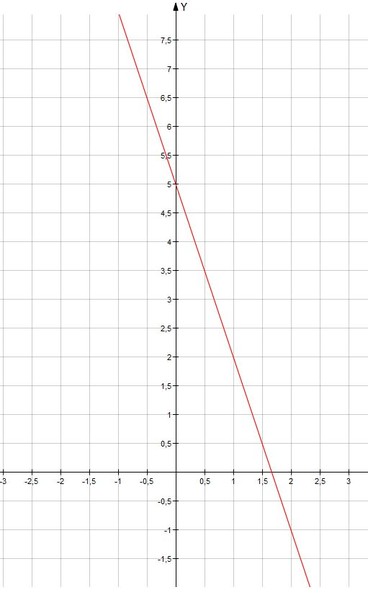 . .. .. ..@ bbox : logi [1, 1] NA
## .. .. .. ..@ proj4string:Formal class 'CRS' [package "sp"] with 1 slot
## .. .. .. .. .. ..@ projargs: chr NA
## .. ..@ diagnostic :'data.frame': 0 obs. of 0 variables
## .. ..@ restrictions:'data.frame': 0 obs. of 0 variables
## $ competing :'data.frame': 1 obs. of 3 variables:
## ..$ series : chr "CHEWACLA"
## ..$ competing: chr "OAKBORO"
## ..$ family : chr "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts"
## $ geomcomp :'data.frame': 3 obs. of 9 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Interfluve : num [1:3] 1 0 0.182
## ..$ Crest : num [1:3] 0 0 0.0267
## ..$ Head Slope : int [1:3] 0 0 0
## ..$ Nose Slope : int [1:3] 0 0 0
## ..$ Side Slope : num [1:3] 0 0 0.791
## ..$ Base Slope : int [1:3] 0 1 0
## ..$ n : int [1:3] 3 1 187
## ..$ shannon_entropy: num [1:3] 0 0 0.368
## $ hillpos :'data.
. .. .. ..@ bbox : logi [1, 1] NA
## .. .. .. ..@ proj4string:Formal class 'CRS' [package "sp"] with 1 slot
## .. .. .. .. .. ..@ projargs: chr NA
## .. ..@ diagnostic :'data.frame': 0 obs. of 0 variables
## .. ..@ restrictions:'data.frame': 0 obs. of 0 variables
## $ competing :'data.frame': 1 obs. of 3 variables:
## ..$ series : chr "CHEWACLA"
## ..$ competing: chr "OAKBORO"
## ..$ family : chr "fine-loamy, mixed, active, thermic fluvaquentic dystrudepts"
## $ geomcomp :'data.frame': 3 obs. of 9 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Interfluve : num [1:3] 1 0 0.182
## ..$ Crest : num [1:3] 0 0 0.0267
## ..$ Head Slope : int [1:3] 0 0 0
## ..$ Nose Slope : int [1:3] 0 0 0
## ..$ Side Slope : num [1:3] 0 0 0.791
## ..$ Base Slope : int [1:3] 0 1 0
## ..$ n : int [1:3] 3 1 187
## ..$ shannon_entropy: num [1:3] 0 0 0.368
## $ hillpos :'data. frame': 3 obs. of 8 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Toeslope : num [1:3] 0.963 0.786 0
## ..$ Footslope : num [1:3] 0.0366 0.2143 0
## ..$ Backslope : num [1:3] 0 0 0.636
## ..$ Shoulder : num [1:3] 0 0 0.227
## ..$ Summit : num [1:3] 0 0 0.138
## ..$ n : int [1:3] 82 14 247
## ..$ shannon_entropy: num [1:3] 0.0975 0.3228 0.5577
## $ mtnpos : logi FALSE
## $ terrace :'data.frame': 2 obs. of 5 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Tread : num [1:2] 0.979 1
## ..$ Riser : num [1:2] 0.0213 0
## ..$ n : int [1:2] 94 36
## ..$ shannon_entropy: num [1:2] 0.064 0
## $ flats :'data.frame': 2 obs. of 7 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Dip : num [1:2] 0.1569 0.0667
## ..$ Talf : num [1:2] 0.843 0.867
## .
frame': 3 obs. of 8 variables:
## ..$ series : chr [1:3] "CHEWACLA" "CONGAREE" "WILKES"
## ..$ Toeslope : num [1:3] 0.963 0.786 0
## ..$ Footslope : num [1:3] 0.0366 0.2143 0
## ..$ Backslope : num [1:3] 0 0 0.636
## ..$ Shoulder : num [1:3] 0 0 0.227
## ..$ Summit : num [1:3] 0 0 0.138
## ..$ n : int [1:3] 82 14 247
## ..$ shannon_entropy: num [1:3] 0.0975 0.3228 0.5577
## $ mtnpos : logi FALSE
## $ terrace :'data.frame': 2 obs. of 5 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Tread : num [1:2] 0.979 1
## ..$ Riser : num [1:2] 0.0213 0
## ..$ n : int [1:2] 94 36
## ..$ shannon_entropy: num [1:2] 0.064 0
## $ flats :'data.frame': 2 obs. of 7 variables:
## ..$ series : chr [1:2] "CHEWACLA" "CONGAREE"
## ..$ Dip : num [1:2] 0.1569 0.0667
## ..$ Talf : num [1:2] 0.843 0.867
## . .$ Flat : int [1:2] 0 0
## ..$ Rise : num [1:2] 0 0.0667
## ..$ n : int [1:2] 51 15
## ..$ shannon_entropy: num [1:2] 0.27 0.301
## $ pmkind :'data.frame': 6 obs. of 5 variables:
## ..$ series: chr [1:6] "CHEWACLA" "CHEWACLA" "CONGAREE" "CONGAREE" ...
## ..$ pmkind: chr [1:6] "Alluvium" "Residuum" "Alluvium" "Fluviomarine deposits" ...
## ..$ n : int [1:6] 207 1 72 13 1 264
## ..$ total : int [1:6] 208 208 86 86 86 264
## ..$ P : num [1:6] 0.9952 0.0048 0.8372 0.1512 0.0116 ...
## $ pmorigin :'data.frame': 24 obs. of 5 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ pmorigin: chr [1:24] "Igneous and metamorphic rock" "Sedimentary rock" "Granite and gneiss" "Mixed" ...
## ..$ n : int [1:24] 29 11 2 2 1 1 1 1 1 1 ...
## ..$ total : int [1:24] 51 51 51 51 51 51 51 51 51 51 ...
## ..$ P : num [1:24] 0.5686 0.2157 0.0392 0.0392 0.0196 ...
## $ mlra :'data.
.$ Flat : int [1:2] 0 0
## ..$ Rise : num [1:2] 0 0.0667
## ..$ n : int [1:2] 51 15
## ..$ shannon_entropy: num [1:2] 0.27 0.301
## $ pmkind :'data.frame': 6 obs. of 5 variables:
## ..$ series: chr [1:6] "CHEWACLA" "CHEWACLA" "CONGAREE" "CONGAREE" ...
## ..$ pmkind: chr [1:6] "Alluvium" "Residuum" "Alluvium" "Fluviomarine deposits" ...
## ..$ n : int [1:6] 207 1 72 13 1 264
## ..$ total : int [1:6] 208 208 86 86 86 264
## ..$ P : num [1:6] 0.9952 0.0048 0.8372 0.1512 0.0116 ...
## $ pmorigin :'data.frame': 24 obs. of 5 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ pmorigin: chr [1:24] "Igneous and metamorphic rock" "Sedimentary rock" "Granite and gneiss" "Mixed" ...
## ..$ n : int [1:24] 29 11 2 2 1 1 1 1 1 1 ...
## ..$ total : int [1:24] 51 51 51 51 51 51 51 51 51 51 ...
## ..$ P : num [1:24] 0.5686 0.2157 0.0392 0.0392 0.0196 ...
## $ mlra :'data. frame': 19 obs. of 4 variables:
## ..$ series : chr [1:19] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ mlra : chr [1:19] "129" "135A" "136" "133A" ...
## ..$ area_ac : int [1:19] 6166 3878 929362 128376 78429 59646 29004 13530 10366 2128 ...
## ..$ membership: num [1:19] 0.005 0.003 0.738 0.102 0.062 0.047 0.023 0.011 0.008 0.01 ...
## $ climate.annual :'data.frame': 24 obs. of 12 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:24] "Elevation (m)" "Effective Precipitation (mm)" "Frost-Free Days" "Mean Annual Air Temperature (degrees C)" ...
## ..$ minimum : num [1:24] 0 128.8 177 11.3 986 ...
## ..$ q01 : num [1:24] 7 216.4 188 12.9 1069 ...
## ..$ q05 : num [1:24] 34 247.4 196 13.5 1093 ...
## ..$ q25 : num [1:24] 125 312.2 208 14.9 1136 ...
## ..$ q50 : num [1:24] 192 349.8 218 15.7 1178 ...
## ..$ q75 : num [1:24] 248 441.2 227 16.
frame': 19 obs. of 4 variables:
## ..$ series : chr [1:19] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ mlra : chr [1:19] "129" "135A" "136" "133A" ...
## ..$ area_ac : int [1:19] 6166 3878 929362 128376 78429 59646 29004 13530 10366 2128 ...
## ..$ membership: num [1:19] 0.005 0.003 0.738 0.102 0.062 0.047 0.023 0.011 0.008 0.01 ...
## $ climate.annual :'data.frame': 24 obs. of 12 variables:
## ..$ series : chr [1:24] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:24] "Elevation (m)" "Effective Precipitation (mm)" "Frost-Free Days" "Mean Annual Air Temperature (degrees C)" ...
## ..$ minimum : num [1:24] 0 128.8 177 11.3 986 ...
## ..$ q01 : num [1:24] 7 216.4 188 12.9 1069 ...
## ..$ q05 : num [1:24] 34 247.4 196 13.5 1093 ...
## ..$ q25 : num [1:24] 125 312.2 208 14.9 1136 ...
## ..$ q50 : num [1:24] 192 349.8 218 15.7 1178 ...
## ..$ q75 : num [1:24] 248 441.2 227 16. 4 1276 ...
## ..$ q95 : num [1:24] 348 568.8 235 17.3 1392 ...
## ..$ q99 : num [1:24] 480 740.8 243 17.8 1575 ...
## ..$ maximum : num [1:24] 919 1382.8 300 19.7 2202 ...
## ..$ n : int [1:24] 32689 32689 32689 32689 32689 32689 32689 32689 8392 8392 ...
## $ climate.monthly :'data.frame': 72 obs. of 14 variables:
## ..$ series : chr [1:72] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:72] "ppt1" "ppt2" "ppt3" "ppt4" ...
## ..$ minimum : num [1:72] 61 64 81 63 60 78 83 74 68 53 ...
## ..$ q01 : num [1:72] 74 71 92 71 69 83 92 85 81 72 ...
## ..$ q05 : num [1:72] 82 73 98 75 72 89 100 89 86 76 ...
## ..$ q25 : num [1:72] 93 83 105 83 81 96 108 96 91 82 ...
## ..$ q50 : num [1:72] 105 107 120 88 92 101 116 102 98 86 ...
## ..$ q75 : num [1:72] 115 121 128 95 101 106 123 110 105 91 ...
## ..$ q95 : num [1:72] 131 135 137 111 111 117 133 129 118 100 ...
## .
4 1276 ...
## ..$ q95 : num [1:24] 348 568.8 235 17.3 1392 ...
## ..$ q99 : num [1:24] 480 740.8 243 17.8 1575 ...
## ..$ maximum : num [1:24] 919 1382.8 300 19.7 2202 ...
## ..$ n : int [1:24] 32689 32689 32689 32689 32689 32689 32689 32689 8392 8392 ...
## $ climate.monthly :'data.frame': 72 obs. of 14 variables:
## ..$ series : chr [1:72] "CHEWACLA" "CHEWACLA" "CHEWACLA" "CHEWACLA" ...
## ..$ climate_var: chr [1:72] "ppt1" "ppt2" "ppt3" "ppt4" ...
## ..$ minimum : num [1:72] 61 64 81 63 60 78 83 74 68 53 ...
## ..$ q01 : num [1:72] 74 71 92 71 69 83 92 85 81 72 ...
## ..$ q05 : num [1:72] 82 73 98 75 72 89 100 89 86 76 ...
## ..$ q25 : num [1:72] 93 83 105 83 81 96 108 96 91 82 ...
## ..$ q50 : num [1:72] 105 107 120 88 92 101 116 102 98 86 ...
## ..$ q75 : num [1:72] 115 121 128 95 101 106 123 110 105 91 ...
## ..$ q95 : num [1:72] 131 135 137 111 111 117 133 129 118 100 ...
## . .$ q99 : num [1:72] 149 144 147 122 125 133 143 142 137 109 ...
## ..$ maximum : num [1:72] 248 227 239 150 167 198 220 207 192 158 ...
## ..$ n : int [1:72] 32689 32689 32689 32689 32689 32689 32689 32689 32689 32689 ...
## ..$ month : Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## ..$ variable : Factor w/ 2 levels "Potential ET (mm)",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ soilweb.metadata:'data.frame': 19 obs. of 2 variables:
## ..$ product : chr [1:19] "block diagram archive" "component pedons" "KSSL snapshot" "MLRA membership" ...
## ..$ last_update: chr [1:19] "2019-12-17" "2020-12-08" "2020-03-13" "2020-07-14" ...
.$ q99 : num [1:72] 149 144 147 122 125 133 143 142 137 109 ...
## ..$ maximum : num [1:72] 248 227 239 150 167 198 220 207 192 158 ...
## ..$ n : int [1:72] 32689 32689 32689 32689 32689 32689 32689 32689 32689 32689 ...
## ..$ month : Factor w/ 12 levels "1","2","3","4",..: 1 2 3 4 5 6 7 8 9 10 ...
## ..$ variable : Factor w/ 2 levels "Potential ET (mm)",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ soilweb.metadata:'data.frame': 19 obs. of 2 variables:
## ..$ product : chr [1:19] "block diagram archive" "component pedons" "KSSL snapshot" "MLRA membership" ...
## ..$ last_update: chr [1:19] "2019-12-17" "2020-12-08" "2020-03-13" "2020-07-14" ... д.)
д.) Например, вот так выглядит структура экспорта продукции машиностроения из Евросоюза по ведущим партнерам:
Например, вот так выглядит структура экспорта продукции машиностроения из Евросоюза по ведущим партнерам: ..)
..) Для этого используйте параметр
Для этого используйте параметр  Date('2013-01-01')) %>%
ggplot(mapping = aes(x = time, y = export, fill = sitc06)) +
geom_col(color = 'black', size = 0.2, position = 'dodge')
Date('2013-01-01')) %>%
ggplot(mapping = aes(x = time, y = export, fill = sitc06)) +
geom_col(color = 'black', size = 0.2, position = 'dodge') Для этого используем
Для этого используем  2) +
geom_col() +
coord_polar(theta = 'y')
2) +
geom_col() +
coord_polar(theta = 'y') 5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам')
5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам')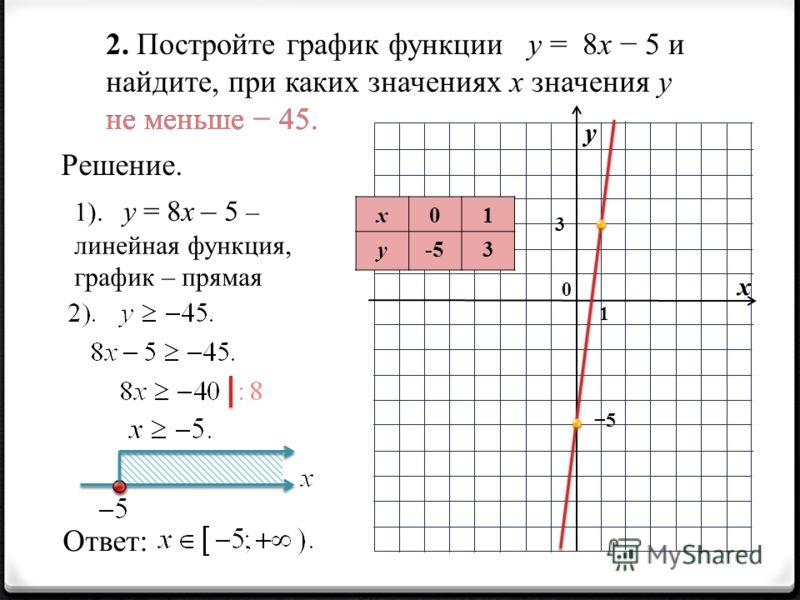 5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт')
5) +
labs(color = "Вид продукции", size = 'Год') +
ggtitle('Соотношение импорта и экспорта в странах Евросоюза (млн долл. США)',
subtitle = 'Данные по ключевым партнерам') +
xlab('Экспорт') +
ylab('Импорт') 5) +
scale_x_log10(breaks = brks, labels = brks / 1000) +
scale_y_log10(breaks = brks, labels = brks / 1000)
5) +
scale_x_log10(breaks = brks, labels = brks / 1000) +
scale_y_log10(breaks = brks, labels = brks / 1000) 5) +
lims(color = 'Machinery and transport equipment')
5) +
lims(color = 'Machinery and transport equipment') Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col(fill = 'plum4', color = 'black', size = 0.2) +
coord_flip() +
geom_label(aes(y = export / 2, label = floor(export / 1000))) # добавляем подписи
Date('2017-01-01')) %>%
ggplot(mapping = aes(x = partner, y = export)) +
geom_col(fill = 'plum4', color = 'black', size = 0.2) +
coord_flip() +
geom_label(aes(y = export / 2, label = floor(export / 1000))) # добавляем подписи 2, color = 'black', size = 0.1) +
geom_point(alpha = 0.5) +
annotate("text", x = 175000, y = 190000, label = "Chemicals", color = 'coral')
2, color = 'black', size = 0.1) +
geom_point(alpha = 0.5) +
annotate("text", x = 175000, y = 190000, label = "Chemicals", color = 'coral') Часть из них входит в состав самой библиотеки. Дополнительные темы можно установить через пакет ggthemes. Чтобы изменить тему оформления ggplot, достаточно прибавить в конце построения графика соответствующую функцию. Например, классическая черно-белая тема получается прибавлением функции
Часть из них входит в состав самой библиотеки. Дополнительные темы можно установить через пакет ggthemes. Чтобы изменить тему оформления ggplot, достаточно прибавить в конце построения графика соответствующую функцию. Например, классическая черно-белая тема получается прибавлением функции 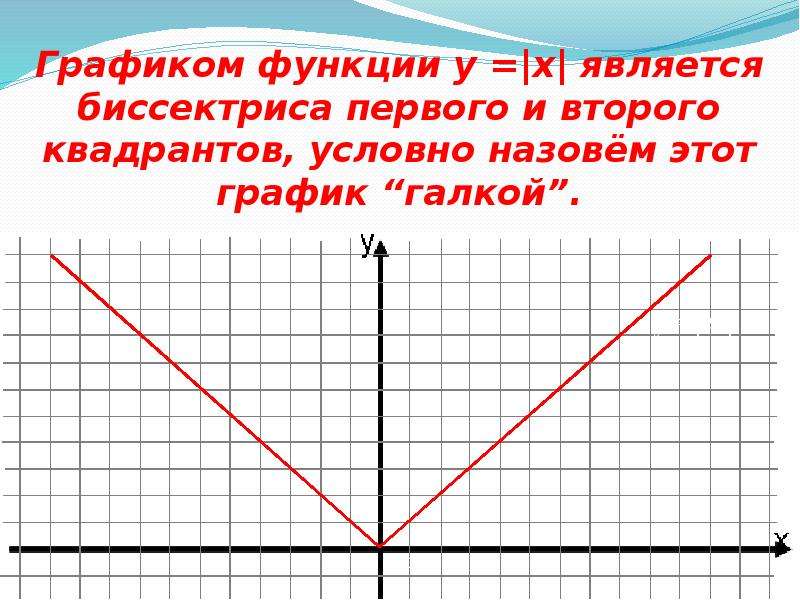

 Также вам потребуется преобразовать таблицу среднемесячных величин к длинной форме, где название месяца будет отдельной переменной (тип — упорядоченный фактор).
Также вам потребуется преобразовать таблицу среднемесячных величин к длинной форме, где название месяца будет отдельной переменной (тип — упорядоченный фактор). : Географический факультет МГУ, 2021. DOI: 10.5281/zenodo.901911
: Географический факультет МГУ, 2021. DOI: 10.5281/zenodo.901911 Подробнее см. раздел «Как формируются котировки».
Подробнее см. раздел «Как формируются котировки».
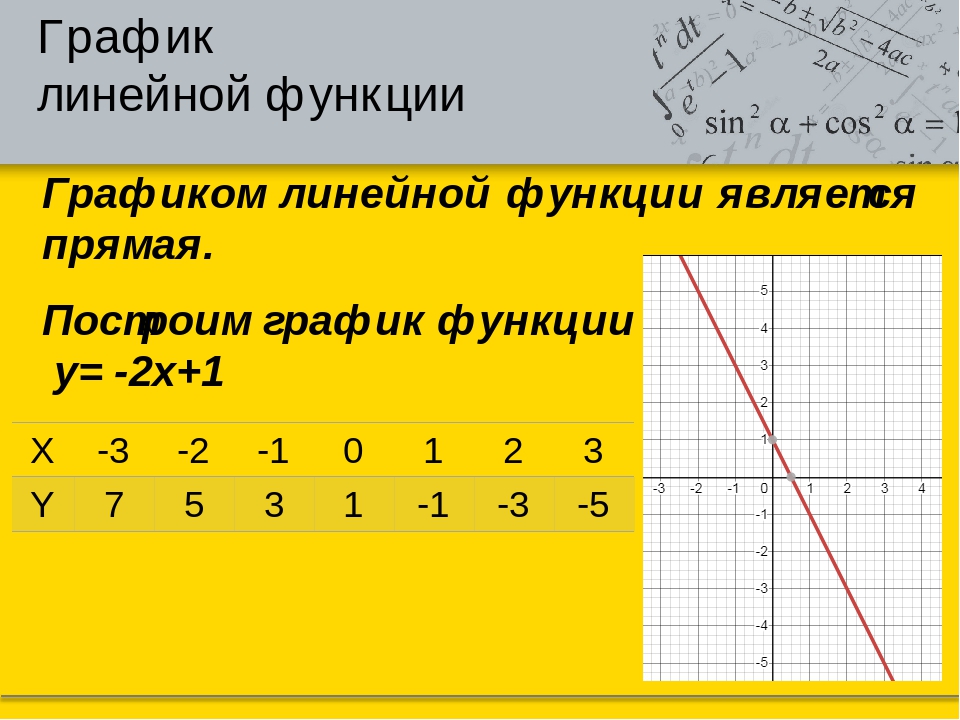


 е. цены внутри диапазона росли (белая свеча - «йо-сен»).
е. цены внутри диапазона росли (белая свеча - «йо-сен»). 
 В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.
Мы можем представить эту взаимосвязь как
В качестве примера рассмотрим пройденное расстояние
через определенный промежуток времени автомобилем, движущимся с постоянной скоростью 40 миль в час.
Мы можем представить эту взаимосвязь как Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро. Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты.При этом соглашении решения
Уравнение d - 40t - это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны
Если мы согласны ссылаться на парные номера в указанном
порядок, в котором первое число относится ко времени, а второе число относится к
расстояния, мы можем сократить приведенные выше решения как (1, 40), (2, 80), (3, 120) и
скоро. Мы называем такие пары чисел упорядоченными парами и ссылаемся на первую и
вторые числа в парах как компоненты.При этом соглашении решения
Уравнение d - 40t - это упорядоченные пары (t, d), компоненты которых удовлетворяют уравнению.
Некоторые упорядоченные пары для t, равного 0, 1, 2, 3, 4 и 5, равны Если в уравнении используются переменные x и y, подразумевается, что заменить -
элементы для x являются первыми компонентами и, следовательно, x - независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения
Если в уравнении используются переменные x и y, подразумевается, что заменить -
элементы для x являются первыми компонентами и, следовательно, x - независимая переменная и
замены y являются вторыми компонентами и, следовательно, y является зависимой переменной.
Например, мы можем получить пары для уравнения Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
Переменная.
Часто бывает проще получить решения, если сначала выразить уравнения в такой форме
потому что зависимая переменная явно выражается через независимые
Переменная.

 Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу.
Если второй компонент положительный, точка находится выше
Горизонтальная ось; если отрицательный, он находится внизу. В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
В разделе 7.2 мы видели, что компонентами упорядоченной пары являются
координаты точки на плоскости. Таким образом, чтобы построить график уравнения с двумя переменными, мы
Изобразите набор упорядоченных пар, которые являются решениями уравнения. Например, мы
может найти некоторые решения уравнения первой степени
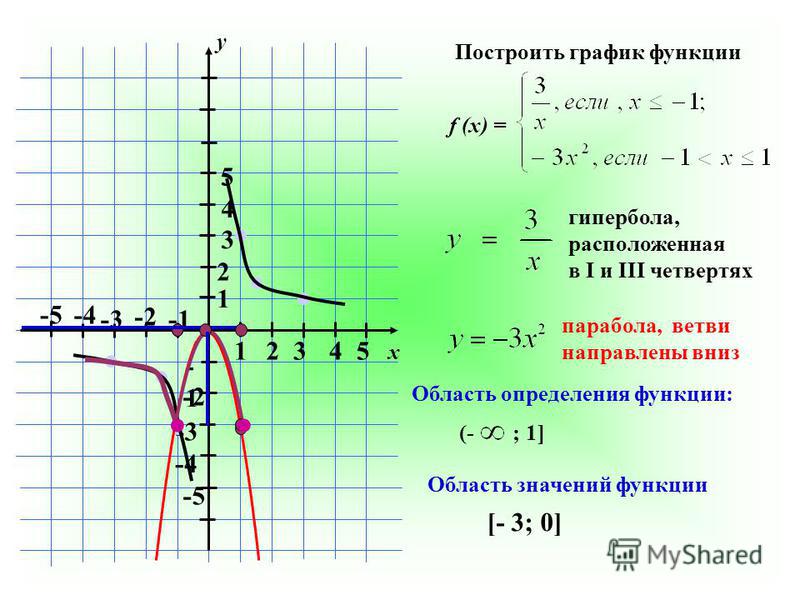

 Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4.
Графическое изображение решений
дает горизонтальную линию, как показано на рисунке
7.4. Решения уравнения с двумя переменными, которые
обычно легче всего найти те, в которых первый или второй компонент
0. Например, если мы подставим 0 вместо x в уравнение
Решения уравнения с двумя переменными, которые
обычно легче всего найти те, в которых первый или второй компонент
0. Например, если мы подставим 0 вместо x в уравнение метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
метод построения графиков. Обратите внимание, что когда мы используем этот метод построения графиков линейного
уравнение, нет никакого преимущества в том, чтобы сначала явно выразить y через x.
 7. Обратите внимание на рис. 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y 2 - y 1 , а изменение по горизонтали (или
расстояние по горизонтали) составляет x 2 - x 1 .
7. Обратите внимание на рис. 7.7, что при переходе от P 1 к P 2 вертикальное изменение (или
расстояние по вертикали) между двумя точками составляет y 2 - y 1 , а изменение по горизонтали (или
расстояние по горизонтали) составляет x 2 - x 1 .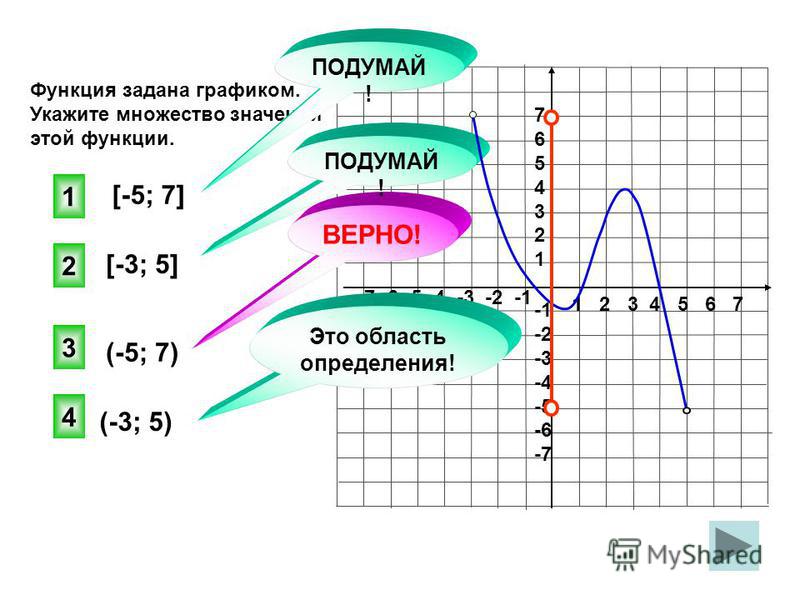 8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y 2 - y 1 равно нулю для любых двух
точек, а наклон линии просто
8 ниже. Наклоны линий, которые
вверх вправо положительны (рисунок 7.8а) и наклоны спускающихся вниз
справа отрицательны (рис. 7.8b). Обратите внимание (рис. 7.8c), поскольку все
точки на горизонтальной линии имеют одинаковое значение y, y 2 - y 1 равно нулю для любых двух
точек, а наклон линии просто В данном случае
В данном случае Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона
Если мы обозначим любую другую точку на прямой как P (x, y) (см. Рис. 7.11 b), то через
формула наклона 12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного
уравнение, имеем
12. Подставив 0 вместо x 1 и b вместо y 1 в форме точечного наклона линейного
уравнение, имеем

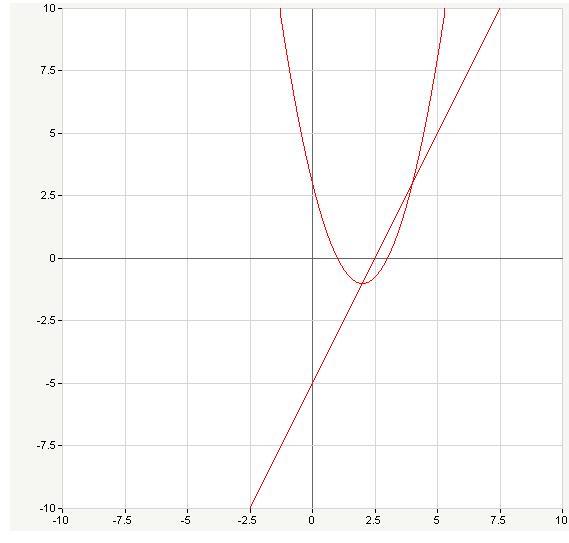 С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем
С другой стороны, (2, 5) не является решением, потому что когда
2 заменяется на x и 5 заменяется на y, мы получаем Затем закрашиваем эту полуплоскость. Всегда можно определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.В таком случае закрашиваем полуплоскость, содержащую контрольную точку; иначе,
закрашиваем другую полуплоскость. Часто (0, 0) - удобная контрольная точка.
Затем закрашиваем эту полуплоскость. Всегда можно определить, какая половина
плоскость заштриховать, выбрав точку (не на линии уравнения Ax + By = C)
и тестирование, чтобы увидеть, является ли упорядоченная пара, связанная с точкой, решением
учитывая неравенство.В таком случае закрашиваем полуплоскость, содержащую контрольную точку; иначе,
закрашиваем другую полуплоскость. Часто (0, 0) - удобная контрольная точка.
 Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x.
Когда х в
символ f (x) заменяется определенным значением, символ представляет значение
выражения для этого значения x. Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y, называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
Координата x точки, в которой линия пересекает ось x.
называется пересечением по оси x линии, а координата y точки, в которой линия
пересекает ось Y, называется пересечением линии. Использование точек пересечения для построения графика
уравнение называется методом построения графика с пересечением.
 Таким образом, когда я подставлю свое значение для x , знаменатель будет отмените, и мне не придется иметь дело с дробями.
Таким образом, когда я подставлю свое значение для x , знаменатель будет отмените, и мне не придется иметь дело с дробями.
 Но я рад, что нарисовал больше, чем две точки, потому что линии, которые начинаются близко к вертикали, могут легко выйти из строя, если я не аккуратен в своей работе.
Но я рад, что нарисовал больше, чем две точки, потому что линии, которые начинаются близко к вертикали, могут легко выйти из строя, если я не аккуратен в своей работе. Каждый раз, когда у вас есть уравнение вида « y равно числу», в котором нет x , на графике всегда будет горизонтальной линией, проходящей через ось y на высоте. какого бы ни было это число.
Каждый раз, когда у вас есть уравнение вида « y равно числу», в котором нет x , на графике всегда будет горизонтальной линией, проходящей через ось y на высоте. какого бы ни было это число.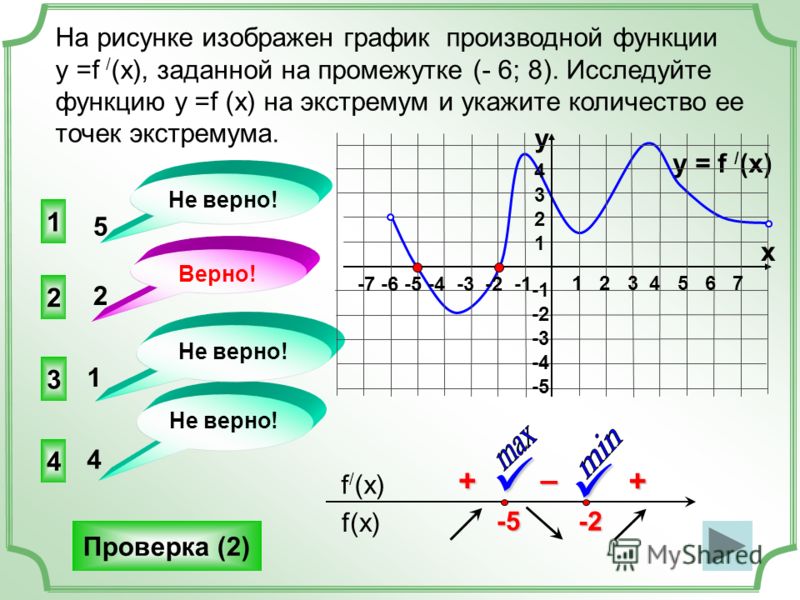 Итак, мой график выглядит так:
Итак, мой график выглядит так:



 7 \ rfloor = 2 $$.
7 \ rfloor = 2 $$. 5 & -2 \\
-1,25 & -2 \\
-1 & -1 \\
-0,75 & -1 \\
-0,5 & -1 \\
-0,25 и -1 \\
0 & 0 \\
0,25 & 0 \\
0,5 & 0 \\
0,75 & 0 \\
1 и 1 \\
1,25 и 1 \\
1.5 и 1 \\
\ hline
\ end {массив}
$$
5 & -2 \\
-1,25 & -2 \\
-1 & -1 \\
-0,75 & -1 \\
-0,5 & -1 \\
-0,25 и -1 \\
0 & 0 \\
0,25 & 0 \\
0,5 & 0 \\
0,75 & 0 \\
1 и 1 \\
1,25 и 1 \\
1.5 и 1 \\
\ hline
\ end {массив}
$$ Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.

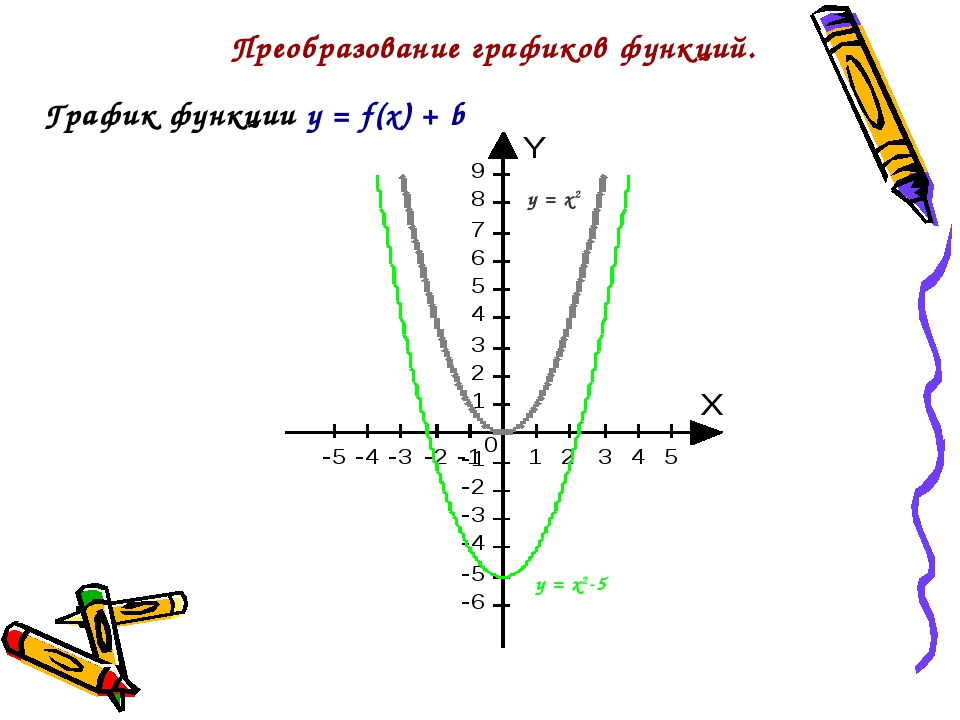 25 + u Шаг 3
25 + u Шаг 3 Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
Теперь мы рассмотрим неравенства по двум переменным. Неравенства по двум переменным имеют множество приложений. Например, если вы управляете бизнесом, вы хотите, чтобы ваш доход превышал ваши расходы, чтобы ваш бизнес приносил прибыль.
 Это кратко показано на (Рисунок)
Это кратко показано на (Рисунок)
 Итак, точка находится на границе.
Итак, точка находится на границе.



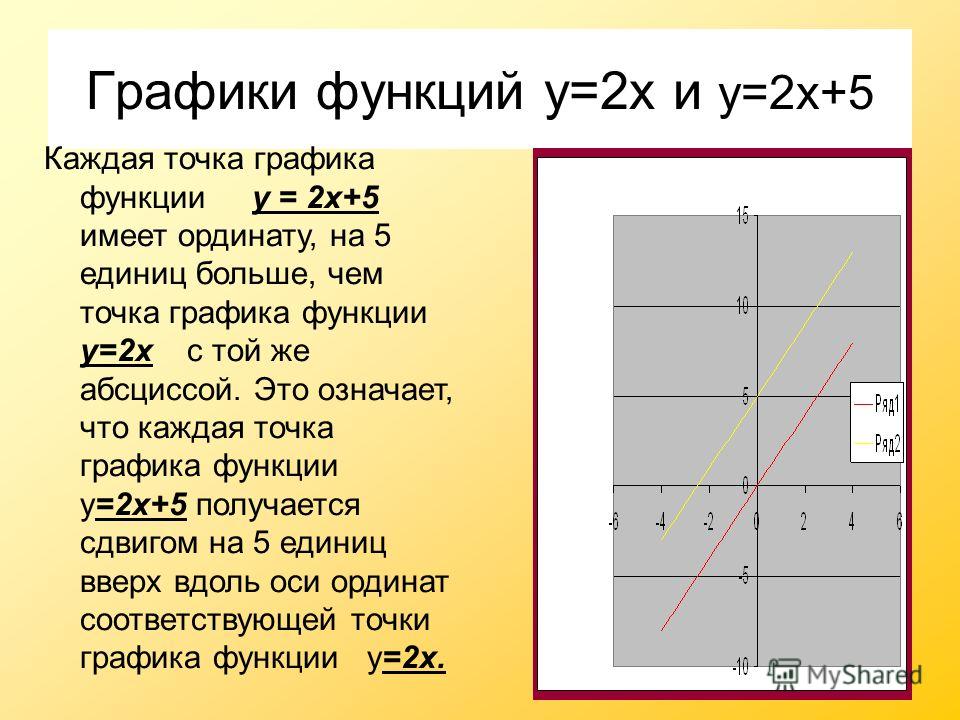
 Сравните значения с уравнением.
Сравните значения с уравнением.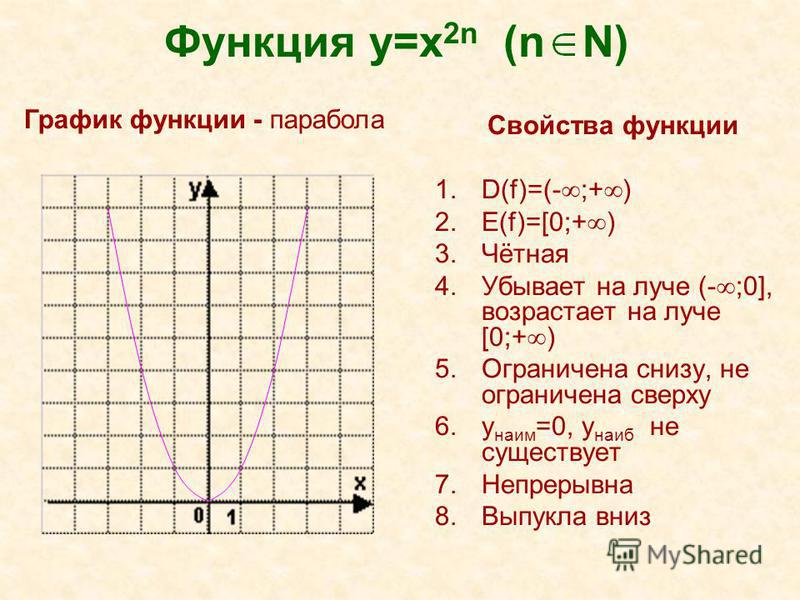
 Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ
Перехват P означает, что, когда количество уроков равно 0, Марджори теряет 250 фунтов стерлингов. Ⓓ 
 Запишите уравнение в форме угла наклона и точки пересечения.
Запишите уравнение в форме угла наклона и точки пересечения.
 Начнем с просмотра рисунка 8. Сразу видно, что график пересекает ось y в точке (0, 4), так что это пересечение y .
Начнем с просмотра рисунка 8. Сразу видно, что график пересекает ось y в точке (0, 4), так что это пересечение y .
 Функция g имеет тот же наклон, но другую точку пересечения y- . Линии I и III имеют одинаковый уклон, потому что они имеют одинаковый уклон. Линия III не проходит через (0, 3), поэтому f должен быть представлен линией I.
Функция g имеет тот же наклон, но другую точку пересечения y- . Линии I и III имеют одинаковый уклон, потому что они имеют одинаковый уклон. Линия III не проходит через (0, 3), поэтому f должен быть представлен линией I.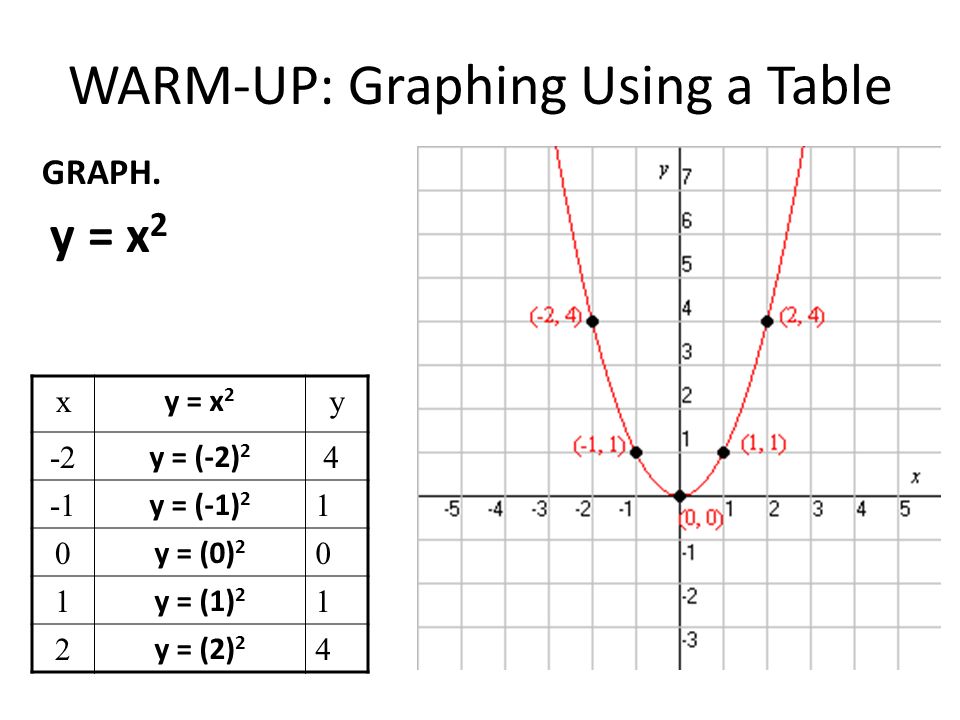 Эта функция представлена линией II.
Эта функция представлена линией II.
 Его можно решить уравнением 0 = mx + b .
Его можно решить уравнением 0 = mx + b .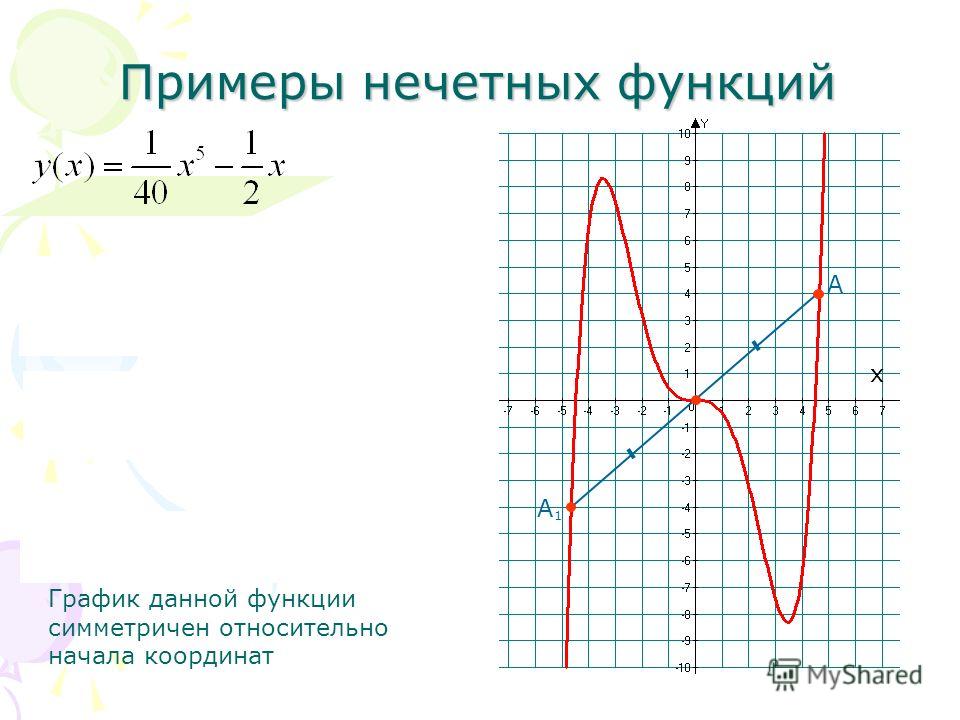 Горизонтальная линия указывает на постоянный выход или значение y . На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение выходных сигналов между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m = 0 в уравнении [латекс] f \ left (x \ right) = mx + b [/ latex], уравнение упрощается до [latex] f \ left (x \ right) = b [/ latex].Другими словами, значение функции постоянно. Этот график представляет функцию [латекс] f \ left (x \ right) = 2 [/ latex].
Горизонтальная линия указывает на постоянный выход или значение y . На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение выходных сигналов между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m = 0 в уравнении [латекс] f \ left (x \ right) = mx + b [/ latex], уравнение упрощается до [latex] f \ left (x \ right) = b [/ latex].Другими словами, значение функции постоянно. Этот график представляет функцию [латекс] f \ left (x \ right) = 2 [/ latex]. Поскольку это входное значение отображается более чем на одно выходное значение, вертикальная линия не представляет функцию.Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.
Поскольку это входное значение отображается более чем на одно выходное значение, вертикальная линия не представляет функцию.Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен. 
 ..
.. Нам нужно будет переставить это так, чтобы "y" находилось слева само по себе:
Нам нужно будет переставить это так, чтобы "y" находилось слева само по себе: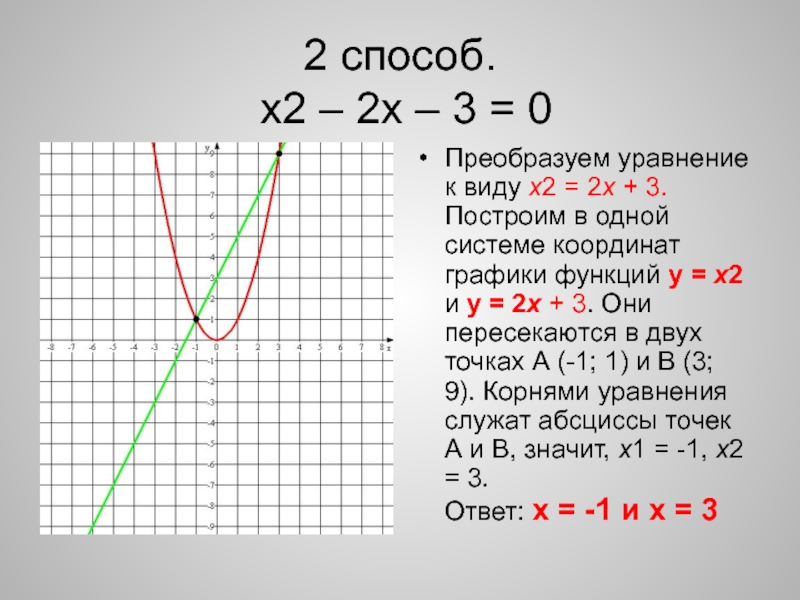
Ваш комментарий будет первым