2 х 4 график
Вы искали 2 х 4 график? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 x 2 функция, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «2 х 4 график».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 2 х 4 график,4 x 2 функция,x 2 4x y график,y 2 х 4,y 4x 2 2x,y 4x x2 график,y x 2 2x 4,y x 2 4x построить график,y x 4 x 2,y x 4x 2,y x2 4x график,график 2x 4,график y x 2 4x,график функции 2 x 4,график функции 4x x 2,график функции y 2x 4,график функции y x 2 4,график функции y x2 4,график функции у 4х2,график функции х 2 4,график х 2 4,постройте график x 2 y 4,постройте график функции y x 2 4 x 2,у 2 4х,у 2 х 4,у 2х 4,у х2 4х,функция 4 x 2,функция 4 х 2.
Где можно решить любую задачу по математике, а так же 2 х 4 график Онлайн?
Решить задачу 2 х 4 график вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
ГИА — построение графиков функций со знаком модуля / Sandbox / Habr
Всем привет! Хотел бы сегодня объяснить такую тему, как построение графиков.
2 или y=1/x. А как строить графики со знаком модуля?Задача 1. Построить графики функций y=|x| y=|x-1|.
Решение. Сравним его с графиком функции y=|x|.При положительных x имеем |x|=x. Значит, для положительных значений аргумента график y=|x| совпадает с графиком y=x, то есть эта часть графика является лучём, выходящим из начала координат под углом 45 градусов к оси абсцисс. При x< 0 имеем |x|= -x; значит, для отрицательных x график y=|x| совпадает с биссектрисой второго координатного угла.
y=|x|
Для построения берём точки (-2; 2) (-1; 1) (0; 0) (1; 1) (2; 2).
Теперь график y=|x-1|. Если А — точка графика у=|x| с координатами (a;|a|), то точкой графика y=|x-1| с тем же значением ординаты Y будет точка A1(a+1;|a|).
(Почему?) Эту точку второго графика можно получить из точки А(a;|a|) первого графика сдвигом параллельно оси Ox вправо. Значит, и весь график функции y=|x-1|получается из графика функции y=|x| сдвигом параллельно оси Ox вправо на 1.
Построим графики:
y=|x-1|
Для построения берём точки (-2; 3) (-1; 2) (0; 1) (1; 0) (2; 1).
Это была простенькая задачка. Теперь то, что многих приводит в ужас.
Задача 2. Постройте график функции y=3*|x-4| — x + |x+1|.
Решение. Найдем точки, в которых подмодульные выражения обращаются в нуль, т.е. так называемые «критические» точки функции. Такими точками будут х=-1 и х=4. В этих точках подмодульные выражения могут изменить знак.
Пусть x<-1. Тогда х+1<0, |x+1|=-x-1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(-х-1)= -5х+11.
Пусть -1< = x < = 4. Тогда х+1>0, |x+1|=x+1; x-4<0, |x-4|=-x+4; Следовательно y= 3(-х+4)-х+(х+1)= -3х+13.
Пусть х>4. Тогда х+1>0, |x+1|=x+1, x-4>0; |x-4|=x-4; Следовательно у= 3(х-4)-х+х+1= 3х-11.
Итак, всем спасибо! Теперь мы получили ту базу знаний, необходимую для построения графиков со знаком модуля! А то его так все боятся.
Вот ссылка, которая поможет вам проверить ваши построения:
Постройте график функции и найдите значение k
Постройте график функции y=|x-3|-|x+3| и найдите значение k, при которых прямая y=kx имеет с графиком данной функции ровно одну общую точку.
Решение:
Разберем как строить график с модулем.
y=|x-3|-|x+3|
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3).
Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—(x-3)-(—(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—(x-3)-(+(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.
Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+(x-3)-(+(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
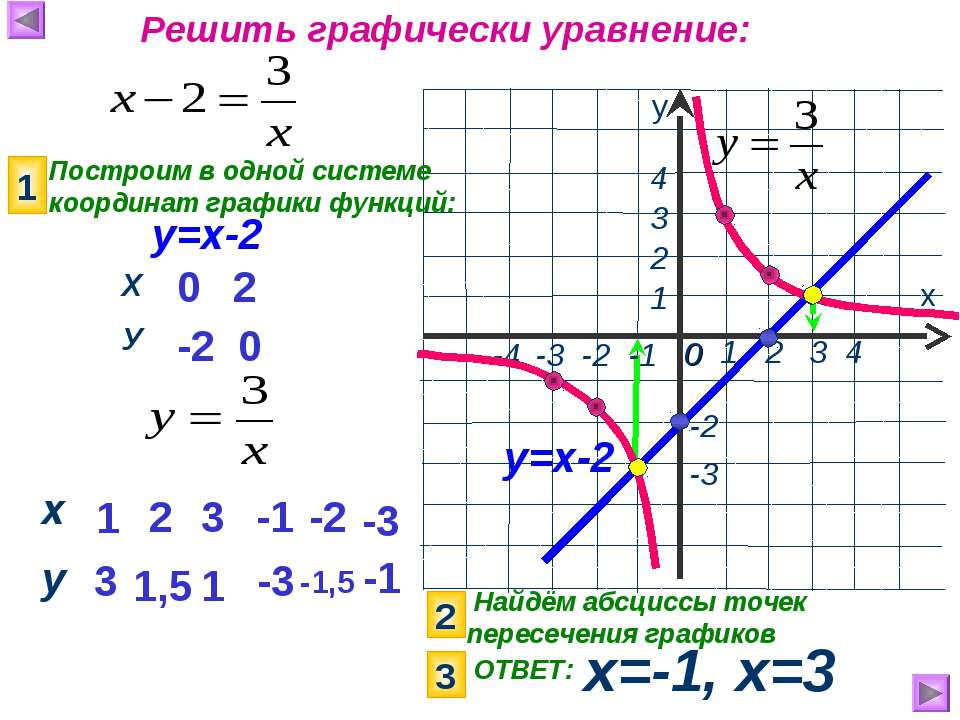
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.
Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U[0;+∞) прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Преобразование графиков функций
Преобразование графиков функций
В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции
Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.
Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:
- Вычленение базовой функции, собственно, график которой мы и преобразовываем.
- Определения порядка преобразований.
Именно на этих моментах мы и остановимся подробнее.
Рассмотрим внимательно функцию
В ее основе лежит функция . Назовем ее базовой функцией.
При построении графика функции мы совершаем преобразования графика базовой функции .
Если бы мы совершали преобразования функции в том же порядке , в каком находили ее значение при определенном значении аргумента, то
Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.
Преобразования аргумента.
1. f(x) f(x+b)
1. Строим график фунции
2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц
- влево, если b>0
- вправо, если b<0
Построим график функции
1. Строим график функции
2. Сдвигаем его на 2 единицы вправо:
2. f(x) f(kx)
1. Строим график фунции
2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.
Построим график функции .
1. Строим график функции
2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:
3. f(x) f(-x)
1. Строим график фунции
2. Отображаем его симметрично относительно оси OY.
Построим график функции .
1. Строим график функции
2. Отображаем его симметрично относительно оси OY:
4. f(x) f(|x|)
1. Строим график функции
2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:
График функции выглядит так:
Построим график функции
1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):
2. Часть графика, расположенную левее оси OY (x<0) стираем:
3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:
Важно! Два главных правила преобразования аргумента.
1. Все преобразования аргумента совершаются вдоль оси ОХ
2. Все преобразования аргумента совершаются «наоборот» и «в обратном порядке».
Например, в функции последовательность преобразований аргумента такая:
1. Берем модуль от х.
2. К модулю х прибавляем число 2.
Но построение графика мы совершали в обратном порядке:
Сначала выполнили преобразование 2. — сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы «наоборот»)
Затем выполнили преобразование f(x) f(|x|).
Коротко последовательность преобразований записывается так:
Теперь поговорим о преобразовании функции. Преобразования совершаются
1. Вдоль оси OY.
2. В той же последовательности, в какой выполняются действия.
Вот эти преобразования:
1. f(x)f(x)+D
1. Строим график функции y=f(x)
2. Смещаем его вдоль оси OY на |D| единиц
- вверх, если D>0
- вниз, если D<0
Построим график функции
1.
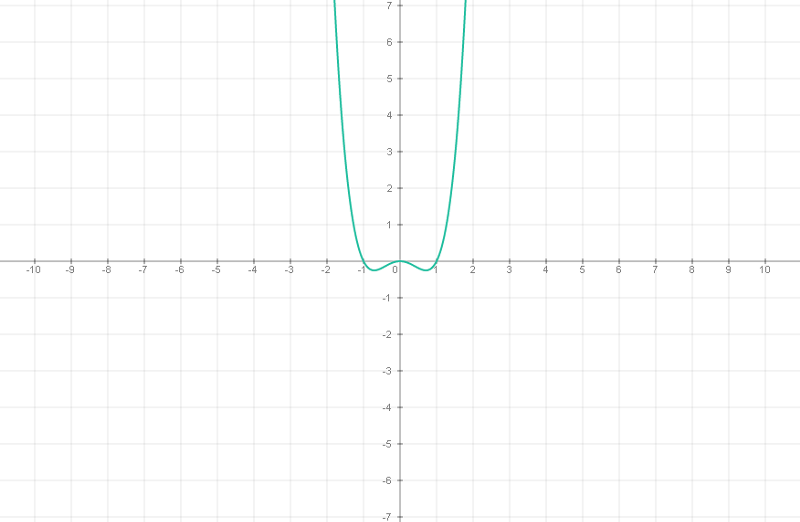Строим график функции
2. Смещаем его вдоль оси OY на 2 единицы вверх:
2. f(x)Af(x)
1. Строим график функции y=f(x)
2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.
Построим график функции
1. Построим график функции
2. Ординаты всех точек графика умножим на 2:
3. f(x)-f(x)
1. Строим график функции y=f(x)
2. Отображаем его симметрично относительно оси ОХ.
Построим график функции .
1. Строим график функции .
2. Отображаем его симметрично относительно оси ОХ.
4. f(x)|f(x)|
1. Строим график функции y=f(x)
2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.
Построим график функции
1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:
2.
Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:
И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:
y=f(x) |y|=f(x)
1. Строим график функции y=f(x)
2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
Построим график уравнения
1. Строим график функции :
2. Часть графика, расположенную ниже оси ОХ стираем:
3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.
И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции
График этой функции выглядит так:
И.
В. Фельдман, репетитор по математике.
Построение графиков функций геометрическими методами / math5school.ru
График функции y=f(x)+a
График функции y=f(x–a)
График функции y=kf(x), k>0
График функции y=f(kx), k>0
График функции y=–f(x)
График функции y=f(–x)
График функции y=|f(x)|
График функции y=f(|x|)
График функции
y=f(x)+aСпособ построения: параллельный перенос графика функции y=f(x) вдоль оси Oy на а единиц вверх, если a>0, и на |a| единиц вниз, если a<0.
График функции
y=f(x–a)Способ построения: параллельный перенос графика функции y=f(x) вдоль оси Ox на а единиц вправо, если a>0, и на |a| единиц влево, если a<0.
График функции
y=kf(x), k>0Способ построения: растяжение графика функции y=f(x) вдоль оси Oy относительно оси Ox в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1.
График функции
y=f(kx), k>0Способ построения: сжатие графика функции y=f(x) вдоль оси Ox относительно оси Oy в k раз, если k>1, и растяжение в 1/k раз, если 0<k<1.
График функции
y=–f(x)Способ построения: симметричное отражение графика функции y=f(x) относительно оси Ox.
График функции
y=f(–x)Способ построения: симметричное отражение графика функции y=f(x) относительно оси Oy.
График функции
y=|f(x)|Способ построения: часть графика функции y=f(x), расположенная ниже оси Ox, симметрично отражается относительно этой оси, остальная его часть остаётся без изменения.
График функции
y=f(|x|)Способ построения: часть графика функции y=f(x), расположенная правее оси Oy и на ней, остаётся без изменения, а остальная его часть заменяется симметричным отображением относительно оси Oy части графика, расположенной правее оси Oy.
Смотрите также:
Таблицы чисел
Алгебраические тождества
Степени
Арифметический корень n-й степени
Логарифмы
Графики элементарных функций
Тригонометрия
Таблицы значений тригонометрических функций
Треугольники
Четырёхугольники
Многоугольники
Окружность
Площади геометрических фигур
Прямые и плоскости
Многогранники
Тела вращения
Постройте график функции y x2 4x 3.
Квадратичная и кубическая функции. Основные свойства квадратичной функцииРазберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2.
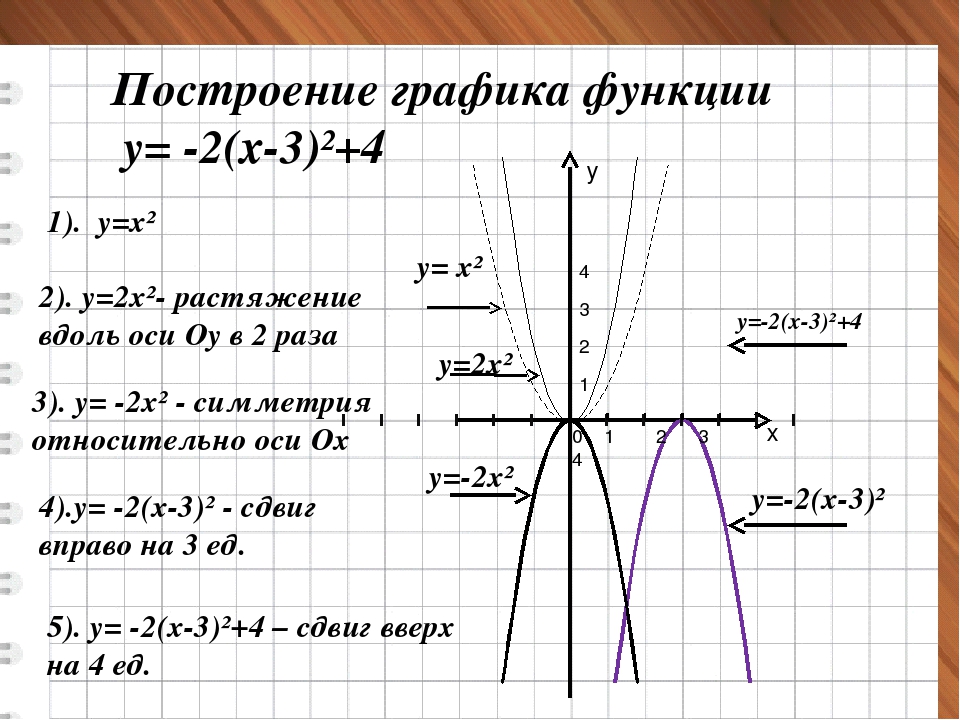Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.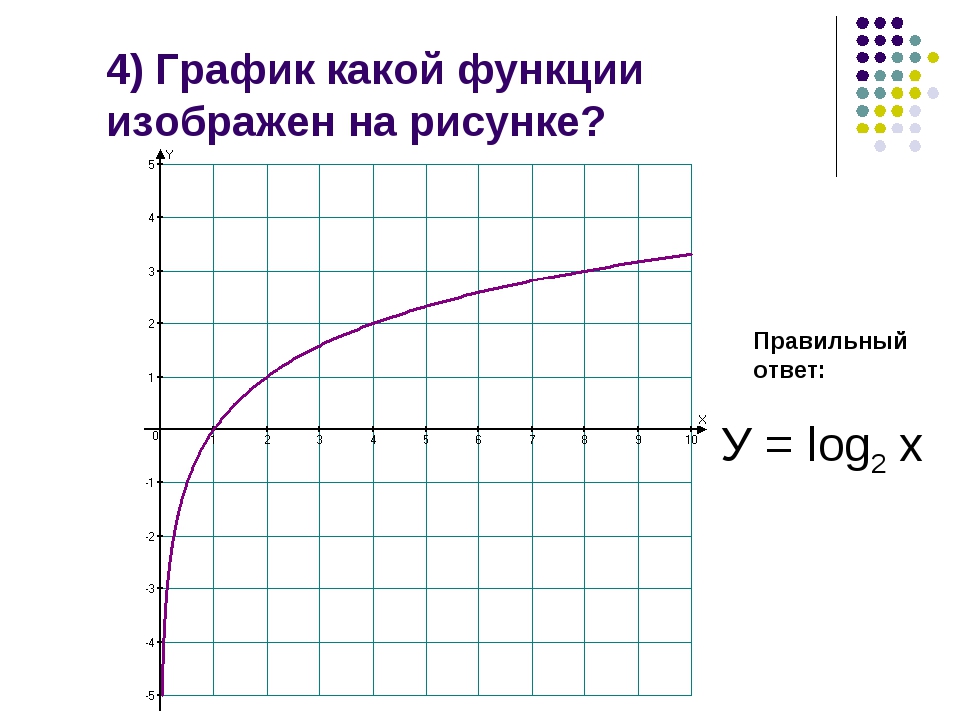
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. Имейте в виду, что нули имеют не все функции, но это первый шаг процесса построения графика любой функции.
{2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.
у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх.
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Функция y=x^2 называется квадратичной функцией.
Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Графические линейные уравнения: больше примеров
Purplemath
Во всех предыдущих упражнениях, которые мы сделали, уравнения, которые нам давали, были решены для одной из переменных, обычно y .
Однако иногда нам дают уравнения, которые не решены. В таком случае обычно проще всего сначала заняться алгеброй, чтобы решить уравнение (обычно для « y =»), чтобы упростить нашу жизнь.(Возможно, вы видели, что это называется «решение буквальных уравнений».) Необязательно, чтобы мы сначала занимались алгеброй, но мы можем сначала решить уравнение, а затем просто вставить-н-пыхтеть, или мы можем вставить уравнение, как указано а затем выполните решение для каждого значения плагина. Первое обычно позволяет сэкономить время по сравнению со вторым.
MathHelp.com
В этом примере проще всего сначала решить для « y =».
Это особенно верно, если я использую графический калькулятор для заполнения своей T-диаграммы, потому что графические калькуляторы могут обрабатывать линейные уравнения только в том случае, если они имеют форму « y =». Итак, чтобы облегчить себе задачу, я сначала решу это уравнение алгебраически.
Для этого я вычту 12 из левой части и добавлю –3 y в правую часть. Затем я разделю на 3 и упрощу. Наконец, я переставлю уравнение (поменяв местами стороны), чтобы получить и в левой части, где я привык:
4 x — 12 = 3 y
4 x — 12 = 3 y
(4 x ) / 3 — (12) / 3 = (3 y ) / 3
(4/3) x — 4 = y
y = (4/3) x — 4
Итак, я на самом деле изображаю это уравнение:
Поскольку я собираюсь умножить свои значения x на дробь, проще всего будет выбрать значения x , кратные 3, так что знаменатель сократится.
Вот мой Т-график …
… а вот мой график:
Сначала я решу уравнение для « y =»
Итак, после перестановки сторон, чтобы привести вещи в обычный формат, мое уравнение:
Хорошо, поэтому вычисление точек графика для этого будет беспорядочным, со всеми дробями.Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я просто буду делать все, что в моих силах, когда я пойду на график своих точек:
Из этих точек я рисую свой график:
Обратите внимание, что этот график должен быть больше (с точки зрения минимального и максимального значений оси), чем то, что я нарисовал ранее.
Это потому, что точки были «беспорядочными», поэтому мне нужно было больше очков, и мне нужно, чтобы эти точки были дальше друг от друга, чтобы убедиться, что моя линия верна.Это пример графика, на который стоит потратить дополнительное время и быть осторожным!
Редко можно встретить упражнения по построению графиков с десятичными знаками. Преобразование в дроби может быть полезным, поскольку вы сможете увидеть, какие виды значений x могут быть более полезными.
Десятичная дробь 0,4 совпадает с дробью
4/10 = 2/5. Итак, я могу рассматривать это уравнение как:Это говорит мне, что выбор значений x , кратных 5, с большей вероятностью даст мне красивые, аккуратные точки сюжета.Вот мой Т-график:
Даже если я пропущу несколько точек на концах (что, думаю, я и сделаю), это будет широкий график, по крайней мере, с точки зрения масштаба.
Между прочим, существуют и другие методы построения графиков прямых линий, такие как построение графиков по пересечениям или построение графиков по пересечению y и наклону. Вы должны ожидать, что вам потребуется возможность использовать любой метод, который был (или будет) введен в ваш класс.
URL: https://www.purplemath.com/modules/graphlin4.htm
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске графика прямой линии из таблицы значений. Затем нажмите кнопку и выберите «Использовать таблицу значений для построения графика уравнения» во всплывающем окне, чтобы сравнить свой ответ с ответом Mathway. (Если вы выбрали значения x , кратные 5, значения вашей таблицы почти наверняка будут «лучше» для построения графика, чем значения Mathway.
Но ваша линия должна быть такой же, как у них.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
линий графика
линия графикаПостроение графиков линейных уравнений
График уравнения с двумя переменными представляет все возможные комбинации x и y , которые удовлетворяют уравнению.Другими словами, точки на графике имеют координаты ( x , y ), которые делают утверждение уравнения истинным. В зависимости от природы уравнения и показателей переменных каждое уравнение имеет свой график.
График любого уравнения, в котором есть две переменные, которые имеют степень один, не умножаются друг на друга и не входят в знаменатель дробей, представляет собой прямую линию.
Например, график 2y — x + 4 = 0 представляет собой линию.
Это означает, что если мы найдем все возможные комбинации x и y, которые работают в уравнении, и построим их в системе координат, результатом будет линия. Поскольку две точки определяют линию, если мы распознаем уравнение как линейное уравнение, нам понадобятся только два набора x и y (точек), которые удовлетворяют уравнению для графика. Есть много способов найти эти точки, и их бесконечное количество. Мы рассмотрим построение линий с помощью пересечений по оси x и оси y. Это точки, в которых линия пересекает ось x и ось y соответственно.Мы выбрали эти точки потому, что с ними легче работать. Пересечение линии по оси x является точкой на оси x и, следовательно, имеет нулевую координату y. А точка пересечения линии y — это точка на оси y, имеющая нулевую координату x . Мы собираемся использовать эти факты, чтобы найти недостающие координаты каждой точки.
Сначала мы подставим ноль для y и найдем соответствующие x , а затем подставим ноль для x и найдем соответствующие y .
Пример 1) График 2 y — x + 4 = 0
Если мы подставим 0 для x , мы получим:
2 y — 0 + 4 = 0 Мы вычтем 4 с обеих сторон:
2 y = -4 и разделив на 2, получим y = -2, поэтому у нас есть (0, -2), это перехват y .
Затем мы подставим ноль для y :
2 (0) — x + 4 = 0 Мы вычтем 4 с обеих сторон:
— x = -4 или x = 4, получим наша вторая точка (4,0), это пересечение x
Теперь мы наносим точки и соединяем их.Результирующая линия представляет все комбинации x, y , которые работают в данном уравнении.
Каждая линия имеет крутизну, которая обозначается как уклон . Крутизна линии или ее наклон — это отношение подъема линии (насколько далеко вверх или вниз мы должны пройти, чтобы достичь другой точки) к ее пробегу (насколько далеко вперед или назад мы должны идти). Для приведенной выше линии наклон составляет 2/4 или 1/2, поскольку нам нужно подняться на 2 единицы, а затем на 4 единицы, чтобы перейти от одной точки к другой.
Мы также можем найти наклон, решив сначала наше уравнение для y . Тогда наклон будет коэффициентом x (а оставшееся число будет пересечением по оси Y):
Сначала мы прибавим x к обеим сторонам и вычтем 4: 2 y = x — 4
Затем мы разделим обе стороны на 2: y = x /2 — 2 (это называется формой пересечения угла наклона линии)
Таким образом, наклон равен 1/2, а точка пересечения оси y равна -2.Эта информация может быть полезна в некоторых случаях.
Пример 2) График 4y + 5x = 20
Подставляя ноль для x, мы получаем:
4y = 20 или y = 5
Таким образом, мы получаем точку пересечения с y (0,5)
Подставляя ноль для y, получаем:
5x = 20 или x = 4
Итак, пересечение по оси x равно (4,0)
Обратите внимание, что наклон этой линии равен -5/4, так как нам нужно спуститься на 5 единиц вниз и вперед на 4 единицы, чтобы перейти от одной точки к другой.
И если мы решим для y (изменим форму на наклон-пересечение ), мы сначала должны вычесть 5x с обеих сторон:
4y = -5x + 20, а затем разделить на 4:
y = -5/4 x + 5
Который также показывает, что наклон равен -5/4, а точка пересечения по оси Y равна 5.
Особые случаи:
Иногда нам может потребоваться построить график уравнений только с одной переменной в системе координат.
Например, y = 4 или x = -2 — это уравнения, которые содержат только одну переменную, но их можно построить в виде линий.
В случае y = 4, набор точек, удовлетворяющих уравнению, — это все точки, которые имеют y значение 4 (с любым возможным значением x). Эти точки могут быть представлены горизонтальной линией y = 4.В общем случае на графике все уравнения вида y = C, где C — число, представляет собой горизонтальную линию в точке C.
В случае x = -2, график представляет собой набор всех точек с x значением -2, которые могут быть представлены вертикальной линией с отметкой -2.
Обычно график всех уравнений в форме x = C представляет собой вертикальную линию в точке C.
Вернуться к линейным функциям
Линейные функции и их графики
Обзор линий графика
Напомним, что множество всех решений линейного уравнения может быть представлено на прямоугольной координатной плоскости с помощью прямой линии, проходящей по крайней мере через две точки; эта линия называется ее графиком.Например, чтобы построить график линейного уравнения 8x + 4y = 12, мы сначала решим для y .
8x + 4y = 12 Вычтем 8x с обеих сторон. 4y = −8x + 12 Разделим обе части на 4.y = −8x + 124 Упростим. Y = −8×4 + 124y = −2x + 3
В таком виде мы видим, что y зависит от x ; другими словами, x — это независимая переменная, которая определяет значения других переменных. Обычно мы думаем о x -значении упорядоченной пары ( x , y ) как о независимой переменной.
и y — зависимая переменная Переменная, значение которой определяется значением независимой переменной. Обычно мы думаем о y -значении упорядоченной пары ( x , y ) как о зависимой переменной. Выберите как минимум два x -значения и найдите соответствующие y -значения. Рекомендуется выбирать ноль, некоторые отрицательные числа, а также некоторые положительные числа. Здесь мы выберем пять значений x , определим соответствующие значения y , а затем сформируем репрезентативный набор упорядоченных парных решений.
x | л | y = −2x + 3 | Решения |
|---|---|---|---|
−2 | 7 | y = −2 (−2) + 3 = 4 + 3 = 7 | (-2, 7) |
-1 | 5 | y = −2 (−1) + 3 = 2 + 3 = 5 | (-1, 5) |
0 | 3 | y = −2 (0) + 3 = 0 + 3 = 3 | (0, 3) |
4 | −5 | y = −2 (4) + 3 = −8 + 3 = −5 | (4, −5) |
6 | −9 | y = −2 (6) + 3 = −12 + 3 = −9 | (6, −9) |
Постройте точки и проведите через них линию с помощью линейки.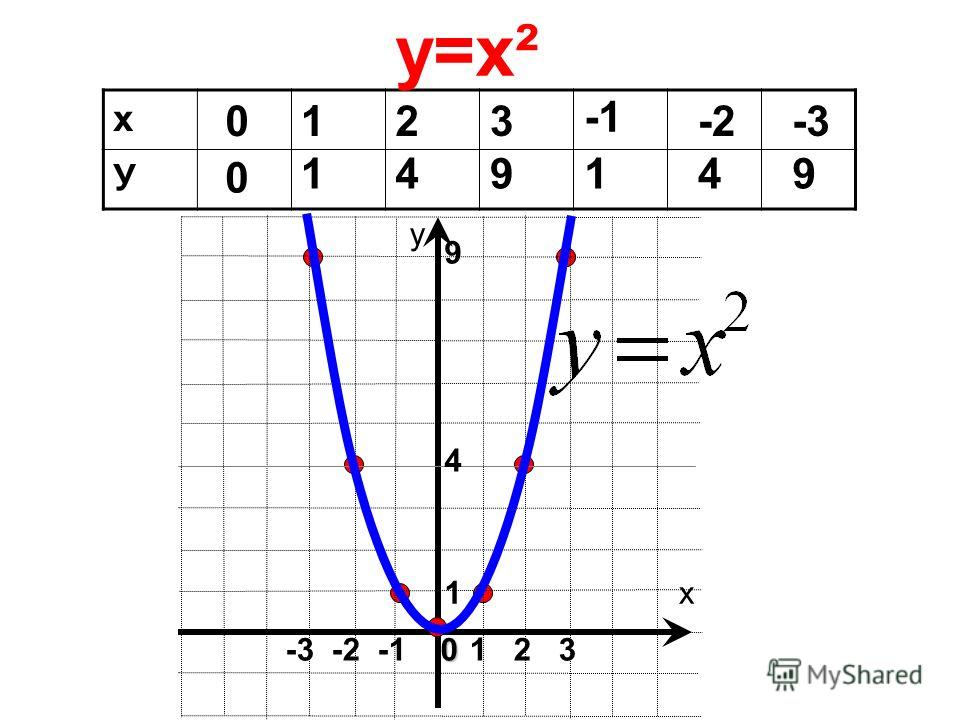
Обязательно добавьте стрелки на обоих концах, чтобы указать, что график неограничен.
Результирующая линия представляет все решения 8x + 4y = 12, которых бесконечно много. Вышеупомянутый процесс описывает метод построения графиков, известный как построение точек. Способ определения графика с использованием конечного числа типичных упорядоченных парных решений. Этот метод будет использоваться для построения графиков более сложных функций по мере продвижения в этом курсе.
Крутизну любого наклона можно измерить как отношение вертикального изменения к горизонтальному.Например, уклон 5% можно записать как 5100, что означает, что на каждые 100 футов вперед высота увеличивается на 5 футов.
В математике мы называем наклон линии наклоном Наклон линии, измеряемый как отношение вертикального изменения к горизонтальному изменению, часто называемый «подъем через пробег», обозначается буквой м .
Вертикальное изменение называется подъемом. Вертикальное изменение между любыми двумя точками на линии. Горизонтальное изменение называется пробегом. Горизонтальное изменение между любыми двумя точками на линии.. Для любых двух точек (x1, y1) и (x2, y2) мы можем получить подъем и пробег, вычитая соответствующие координаты.
Это приводит нас к формуле наклона. Наклон прямой, проходящей через точки (x1, y1) и (x2, y2), задается формулой m = y2 − y1x2 − x1 .. Для любых двух точек (x1, y1) и (x2, y2), наклон определяется как:
Уклон m = riserun = y2 − y1x2 − x1 = ΔyΔx ← Изменение y ← Изменение x
Греческая буква дельта (Δ) часто используется для описания изменения количества.Поэтому наклон иногда описывают с использованием обозначения ΔyΔx, которое представляет изменение y , деленное на изменение x .
Пример 1
Найдите наклон прямой, проходящей через (−3, −5) и (2, 1).
Решение:
Для заданных (−3, −5) и (2, 1) вычислите разницу значений y , деленную на разницу значений x . Будьте последовательны при вычитании координат:
(x1, y1) (x2, y2) (- 3, −5) (2,1)
м = y2 − y1x2 − x1 = 1 — (- 5) 2 — (- 3) = 1 + 52 + 3 = 65
Неважно, какую точку вы считаете первой или второй.Однако, поскольку вычитание не является коммутативным, вы должны позаботиться о том, чтобы вычесть координаты первой точки из координат второй точки в том же порядке. Например, мы получим тот же результат, если применим формулу наклона с переключенными точками:
(x1, y1) (x2, y2) (2,1) (−3, −5)
м = y2 − y1x2 − x1 = −5−1−3−2 = −6−5 = 65
Ответ: m = 65
Убедитесь, что наклон равен 65, построив линию, описанную в предыдущем примере.
Конечно, график не является обязательным; Красота формулы наклона состоит в том, что по любым двум точкам мы можем получить наклон, используя только алгебру.
Пример 2
Найдите значение y , для которого наклон прямой, проходящей через (6, −3) и (−9, y), равен −23.
Решение:
Подставьте данную информацию в формулу наклона.
Наклон (x1, y1) (x2, y2) m = −23 (6, −3) (−9, y)
м = y2 − y1x2 − x1−23 = y — (- 3) −9−6−23 = y + 3 −15
После подстановки в данную информацию остается единственная переменная y .Решать.
−15 (−23) = — 15 (−y + 3 15) 10 = y + 37 = y
Ответ: y = 7
Существует четыре геометрических случая для значения наклона.
Если читать график слева направо, линии с наклоном вверх имеют положительный наклон, а линии с наклоном вниз — отрицательный. В двух других случаях используются горизонтальные и вертикальные линии. Напомним, что если k — действительное число, мы имеем
y = k Горизонтальная линия x = k Вертикальная линия
Например, если мы построим график y = 2, мы получим горизонтальную линию, а если мы построим график x = −4, мы получим вертикальную линию.
Из графиков мы можем определить две точки и рассчитать уклон по формуле наклона.
Горизонтальная линия | Вертикальная линия |
|---|---|
(x1, y1) (x2, y2) (- 3,2) (3, 2) м = y2 − y1x2 − x1 = 2− (2) 3 — (- 3) = 2−23 + 3 = 06 = 0 | (x1, y1) (x2, y2) (- 4, −1) (−4, 1) m = y2 − y1x2 − x1 = 1 — (- 1) −4 — (- 4) = 1 + 1−4 + 4 = 20 Не определено |
Обратите внимание, что точки на горизонтальной линии имеют одинаковые значения y .Следовательно, подъем равен нулю и, следовательно, наклон равен нулю. Точки на вертикальной линии имеют одинаковые значения x .
Следовательно, пробег равен нулю, что приводит к неопределенному уклону. В целом
Линейные функции
Для любого линейного уравнения в стандартной форме Любая невертикальная линия может быть записана в стандартной форме ax + by = c., Ax + by = c, мы можем решить для y , чтобы получить форму пересечения наклона Любая невертикальная линия может быть записана в форма y = mx + b, где м — наклон, а (0, b ) — пересечение y ., у = mx + b. Например,
3x − 4y = 8 ← Стандартная форма − 4y = −3x + 8y = −3x + 8−4y = −3x − 4 + 8−4y = 34x − 2 ← Форма пересечения наклона
Где x = 0, мы видим, что y = −2 и, следовательно, (0, −2) — решение для упорядоченной пары. Это точка, в которой график пересекает ось y и называется пересечением y Точка (или точки), где график пересекает ось y , выраженную в виде упорядоченной пары (0, y ) .
. Мы можем использовать эту точку и наклон как средство для быстрого построения линии.Например, чтобы построить график y = 34x − 2, начните с точки пересечения y (0, −2) и отметьте наклон, чтобы найти вторую точку. Затем используйте эти точки, чтобы построить линию следующим образом:
Тест с вертикальной линией показывает, что этот график представляет функцию. Кроме того, домен и диапазон состоят из всех действительных чисел.
В общем случае линейная функция Любая функция, которую можно записать в форме f (x) = mx + b, является функцией, которую можно записать в форме f (x) = mx + b Линейная функция где уклон м и b представляют любые действительные числа.Поскольку y = f (x), мы можем использовать y и f (x) как взаимозаменяемые, а упорядоченные парные решения на графе (x, y) можно записать в форме (x, f (x)).
(х, у) ⇔ (х, е (х))
Мы знаем, что любой перехват y будет иметь значение x , равное нулю.
Следовательно, перехват y может быть выражен как упорядоченная пара (0, f (0)). Для линейных функций
f (0) = m (0) + b = b
Следовательно, y -перехват любой линейной функции равен (0, b).Чтобы найти точку пересечения x Точка (или точки), где график пересекает ось x , выраженную в виде упорядоченной пары ( x , 0)., Точка, в которой функция пересекает ось x , находим x , где y = 0 или f (x) = 0.
Пример 3
Изобразите линейную функцию f (x) = — 53x + 6 и обозначьте точку пересечения x .
Решение:
Из функции мы видим, что f (0) = 6 (или b = 6) и, таким образом, y -перехват равен (0, 6).Также мы можем видеть, что наклон m = −53 = −53 = riserun. Начиная с точки пересечения и , отметьте вторую точку на 5 единиц ниже и на 3 единицы вправо. Проведите линейкой линию, проходящую через эти две точки.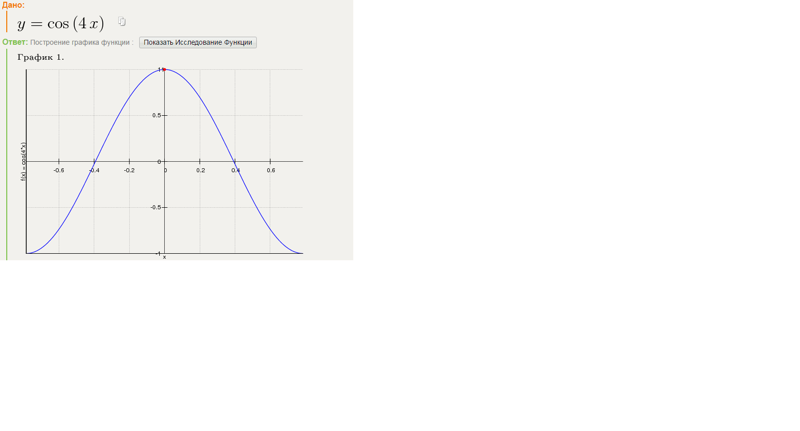
Чтобы определить интервал x , найдите значение x , при котором функция равна нулю. Другими словами, определите x , где f (x) = 0.
f (x) = — 53x + 60 = −53x + 653x = 6 (35) 53x = (35) 6x = 185 = 335
Следовательно, интервал x равен (185,0).Общее правило — помечать все важные моменты, которые нельзя четко прочитать на графике.
Ответ:
Пример 4
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .
Решение:
Мы начинаем с чтения наклона графика. В этом случае начисляются два балла, и мы видим, что
м = стояк = −23
Кроме того, интервал y равен (0, 3) и, следовательно, b = 3.
Мы можем подставить в уравнение любую линейную функцию.
г (х) = mx + b ↓↓ g (x) = — 23x + 3
Чтобы найти x -пересечение, мы устанавливаем g (x) = 0 и решаем относительно x .
г (x) = — 23x + 30 = −23x + 323x = 3 (32) 23x = (32) 3x = 92 = 412
Ответ: g (x) = — 23x + 3; x -перехват: (92,0)
Затем рассмотрите горизонтальные и вертикальные линии. Используйте тест вертикальной линии, чтобы убедиться, что любая горизонтальная линия представляет функцию, а вертикальная — нет.
Для любой горизонтальной линии тест вертикальной линии показывает, что каждое значение x в домене соответствует ровно одному значению y в диапазоне; это функция. Вертикальная линия, с другой стороны, не проходит тест вертикальной линии; это не функция. Вертикальная линия представляет собой набор упорядоченных пар, в которых все элементы в домене одинаковы.
Это нарушает требование, согласно которому функции должны связывать ровно один элемент в диапазоне с каждым элементом в домене.Резюмируем следующим образом:
Горизонтальная линия | Вертикальная линия | |
|---|---|---|
Уравнение: | y = 2 | х = −3 |
Перехват по оси x: | Нет | (−3,0) |
Y-перехват: | (0,2) | Нет |
Домен: | (-∞, ∞) | {−3} |
Диапазон: | {2} | (-∞, ∞) |
Функция: | Есть | № |
Горизонтальную линию часто называют постоянной функцией .
Дано любое действительное число c ,
f (x) = c Константа функция
Пример 5
Постройте график постоянной функции g (x) = — 2 и укажите домен и диапазон.
Решение:
Здесь дана постоянная функция, эквивалентная y = −2. Это определяет горизонтальную линию через (0, −2).
Ответ: Домен: ℝ; диапазон: {−2}
Попробуй! График f (x) = 3x − 2 и обозначьте точку пересечения x .
Ответ:
Линейные уравнения и неравенства: графическая интерпретация
Мы можем использовать идеи этого раздела, чтобы развить геометрическое понимание того, что значит решать уравнения вида f (x) = g (x), где f и g — линейные функции. Используя алгебру, мы можем решить линейное уравнение 12x + 1 = 3 следующим образом:
12x + 1 = 312x = 2 (2) 12x = (2) 2x = 4
Решение этого уравнения: x = 4.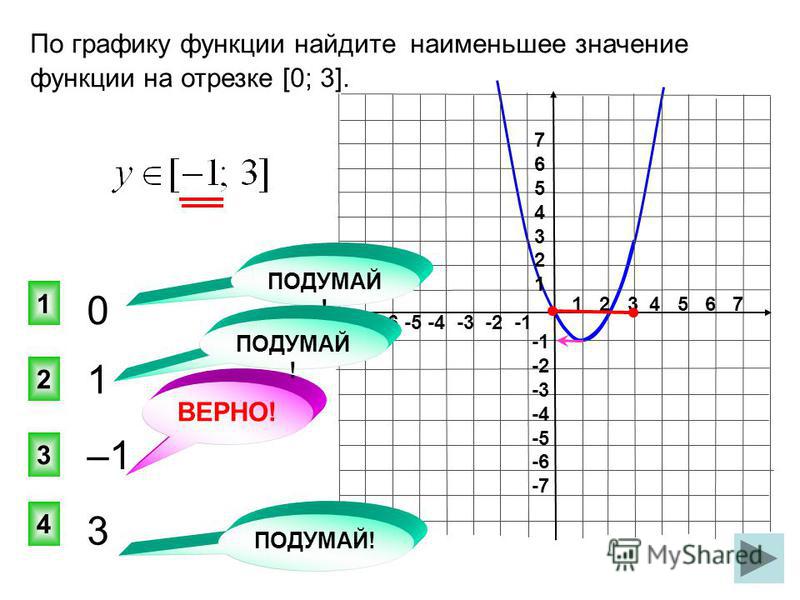
Геометрически это значение x пересечения двух графиков f (x) = 12x + 1 и g (x) = 3. Идея состоит в том, чтобы построить график линейных функций по обе стороны от уравнения и определить, где графики совпадают.
Пример 6
График f (x) = 12x + 1 и g (x) = 3 на одном и том же наборе осей и определите, где f (x) = g (x).
Решение:
Здесь f — линейная функция с наклоном 12 и y -пересечение (0,1).Функция g является постоянной функцией и представляет собой горизонтальную линию. Изобразите обе эти функции на одном наборе осей.
Из графика видно, что f (x) = g (x), где x = 4. Другими словами, 12x + 1 = 3, где x = 4.
Ответ: x = 4
Мы можем немного расширить геометрическую интерпретацию, чтобы решить неравенства. Например, мы можем решить линейное неравенство 12x + 1≥3, используя алгебру, следующим образом:
12x + 1≥312x≥2 (2) 12x≥ (2) 2x≥4
Набор решений состоит из всех действительных чисел, больших или равных 4.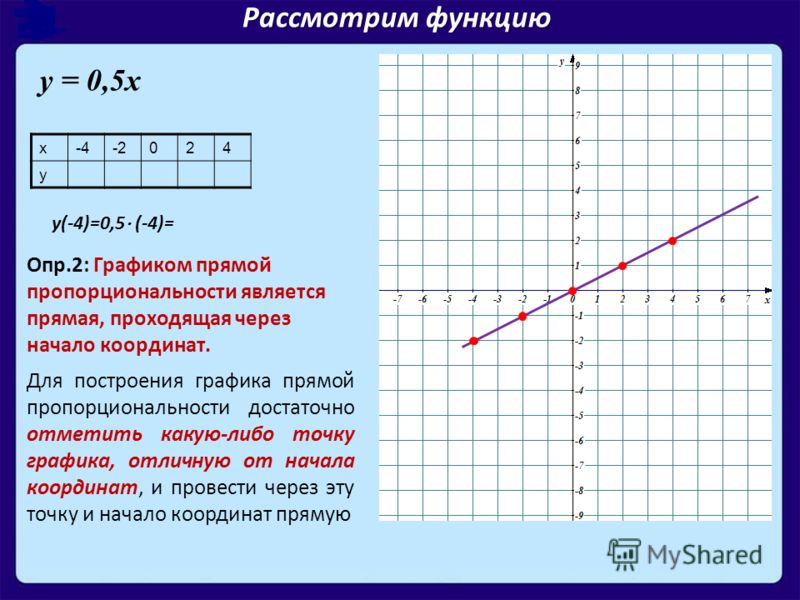
Геометрически это значения x , для которых график f (x) = 12x + 1 лежит выше графика g (x) = 3.
Пример 7
График f (x) = 12x + 1 и g (x) = 3 на одном и том же наборе осей и определить, где f (x) ≥g (x).
Решение:
На графике это заштриховано.
Из графика видно, что f (x) ≥g (x) или 12x + 1≥3, где x≥4.
Ответ: Значения x , решающие неравенство, в интервальной нотации равны [4, ∞).
Основные выводы
- Мы можем построить линии, нанося точки. Выберите несколько значений для x , найдите соответствующие значения y , а затем нанесите на график полученные решения для упорядоченных пар. Проведите линию через точки с помощью линейки, чтобы завершить график.
- Для любых двух точек на прямой мы можем вычислить наклон алгебраически, используя формулу наклона, m = riserun = y2 − y1x2 − x1 = ΔyΔx.
- Используйте форму пересечения наклона y = mx + b, чтобы быстро нарисовать график линии.От точки пересечения и (0, b) отметьте наклон, чтобы определить вторую точку. Поскольку две точки определяют линию, проведите линию через эти две точки линейкой, чтобы завершить график.
- Линейные функции имеют вид f (x) = mx + b, где наклон м и b — действительные числа. Чтобы найти перехват x , если он существует, установите f (x) = 0 и найдите x .
- Поскольку y = f (x), мы можем использовать y и f (x) как взаимозаменяемые.Любая точка на графике функции может быть выражена с помощью обозначения функции (x, f (x)).
Тематические упражнения
(-52,14) и (-12,54)
(−4, −3) и (−2, −3)
(12, -1) и (-1, -32)
м = 32; (6,10), (−4, у)
м = −13; (−6,4), (9, у)
м = −4; (−2,5), (−1, y)
м = 3; (1, −2), (−2, y)
м = 15; (1, у), (6,15)
м = −34; (−1, у), (−4,5)
Часть A: Графические линии по точкам построения
Найдите пять упорядоченных парных решений и график.
Найдите наклон прямой, проходящей через заданные точки.
Найдите значение y , для которого наклон прямой, проходящей через данные точки, имеет данный наклон.
По графику определите наклон.
Часть B: Линейные функции
Найдите точки пересечения x и y и используйте их для построения графика следующих функций.
Изобразите линейную функцию и обозначьте точку пересечения x .
Определите линейную функцию, которая определяет данный график, и найдите точку пересечения x .
f (x) = 3x − 2, g (x) = — 2x + 3
f (x) = — 13x, g (x) = — 23x + 1
f (x) = 23x − 1, g (x) = — 43x − 3
f (x) = 32x + 3, g (x) = — 32x − 3
Часть C: Графическая интерпретация линейных уравнений и неравенств
Изобразите графики функций f и g на одном наборе осей и определите, где f (x) = g (x).
Проверьте свой ответ алгебраически.
Постройте график функций f и g на одном и том же наборе осей и определите, где f (x) ≥g (x).
Проверьте свой ответ алгебраически.
Постройте график функций f и g на одном и том же наборе осей и определите, где f (x)
Все ли линейные функции имеют точки пересечения и ? Все ли линейные функции имеют x -перехватов? Объяснять.
Может ли функция иметь более одного перехвата y ? Объяснять.
Как проверка вертикальной линии показывает, что вертикальная линия не является функцией?
Часть D: Обсуждение
ответов
ф (х) = х + 1; (−1,0)
f (x) = — 32x; (0,0)
Математическая сцена — Уравнения III — Урок 3
Математическая сцена — Уравнения III — Урок 3 — Квадратные уравнения| 2008 Rasmus ehf и Jhann sak | Уравнения III |
Урок 3 Пересечение точек графиков
Как мы приступаем к поиску точек, в которых два графика y = f (x) и y = g (x) пересекаются?
Мы уже знаем, как найти график
f (x) пересекает ось x.
Здесь y = 0. Мы вычисляем его, решая
уравнение f (x) = 0.
Когда графики y = f (x) и y =
g (x) пересекаются, оба графа имеют
точно такие же значения x и y. Итак, мы можем найти точку или точки
пересечения путем решения уравнения f (x)
= g (x). Решение этого уравнения даст нам значение (я) x
точка (и) пересечения. Затем мы можем найти значение y, поместив значение для
x, который мы нашли в одном из исходных уравнений.То есть путем расчета
либо f (x), либо g (x).
Пример 1
Рассчитать точку пересечение двух прямых f (x) = 2x — 1 и g (x) = x + 1. Сначала давайте посмотрим на график двух функций. Мы видим смысл пересечение есть (2, 3).
Рассчитываем точку пересечения по решение уравнения f (x) = g (x). То есть:
2х — 1 = х + 1
2х — х = 1 + 1
х = 2
Координата Y теперь может быть найдена вычисление f (2):
f (2) = 2 × 2 — 1 = 3
Точка пересечения — (2,
3) .
Пример показывает, что мы можем найти точку
пересечения двумя способами.
Либо графически, нарисовав два графика в одной системе координат, либо
алгебраически, решив уравнение, такое как в приведенном выше примере.
Некоторые уравнения нельзя решить алгебраически, но мы можем найти решения, которые исправляем до любого количества значащих цифр, используя компьютеры и калькуляторы.
Пример 2
Решите уравнение x 2 — 2x — 3 = 2x — 3 сначала графически, затем алгебраически.
Рисуем графики f (x) = x 2 — 2x — 3 и g (x) = 2x — 3 путем составления таблицы значений и построения графика точки. Как из графика, так и из таблицы значений видно, что графики пересекаются при x = 0 и x = 4 .
Решает алгебраически:
x 2 — 2x — 3 = 2x — 3
x 2 — 4x = 0
х (х — 4) = 0
Получение решений x = 0 и x = 4 .
Пример 3
Решите уравнение x 2 — 1 = 2x — 3
Сначала переместите все условия перейдите к левой части уравнения и упростите.
Это дает x 2 — 2x + 2 = 0
Используем формулу корней квадратного уравнения с a = 1, b = −2 и c = 2.
Число под знаком квадратного корня:
отрицательный, что означает, что это уравнение не имеет решения.
Чтобы понять, почему это так, мы рисуем графики в левой части оригинала.
уравнение
f (x) = x 2 — 1 и правая часть g (x) = 2x — 3.
Мы видим, что парабола f (x) и прямая g (x) не пересекаются.Легко видеть, что мы не может вычислить точку проникновения просто потому, что такой точки нет.
Пример 4
Решите уравнение x 3 — 3x + 2 = x 2 — 2x + 1
Как и в предыдущем примере, мы перемещаем все
слагаемые в левую часть уравнения.
х 3 — 3x + 2 = x 2 — 2x + 1
х 3 — х 2 — х + 1 = 0
(x 3 — x 2 ) — (x — 1) = 0
x 2 (x — 1) — (x — 1) = 0
(х — 1) (х 2 — 1) = 0
(х — 1) (х — 1) (х + 1) = 0
Расчеты показывают, что их всего два решений, x = 1 и x = −1, но кубическое уравнение может иметь три решения.График показывает нам, что происходит.
Графики f (x) = x 2 — 2x + 1 и g (x) = x 3 — 3x + 2 пересекаются только в двух местах, где x = −1 и x = 1, которые были решениями уравнение.
Пример 5
Решите уравнение x 2 = x
Легко видеть, что x = 0 и x = 1 являются решения уравнения, но есть ли еще решения? Это не очень вероятно, но давайте посмотрим на графики.
Назовите левую часть f (x) = x 2 и правую часть g (x) = x.
Помните, что g (x) не может принимать отрицательные значения x, поэтому не может быть никаких
отрицательные точки пересечения.
На графике видно, что точек всего две
пересечения и, следовательно, только два решения уравнения. х = 0 и х =
1.
Вот как решить уравнение расчетом:
| x 2 = x х 4 = х х 4 — х = 0 х (х 3 — 1) = 0 | Квадрат обе части уравнения, чтобы избавиться от квадратного корня . |
Это дает решение x = 0 и x = 1 .
Пример 6
Решите уравнение ln x = x 2 — 1
Это уравнение не так-то просто решить. Если мы
помните определение логарифма, мы видим, что x = 1 делает обе стороны
уравнение равно 0 и, следовательно, является одним решением уравнения.
Мы рисуем
графики, чтобы увидеть, есть ли другие решения.
График показывает нам, что есть два решения. Одно решение — ровно x = 1, поскольку e 0 = 1.
Обратите внимание, что мы выбираем значения x так, чтобы значения y становятся все ближе и ближе друг к другу в таблице значений. Таким образом мы можем выбрать значение x, чтобы получить желаемую точность.| Пример 7 | EXCEL |
Если мы воспользуемся графическим калькулятором, то сможем найти решение уравнения ln x = x 2 — 1 намного проще.
Рисуем графики обеих сторон уравнение и используйте Zoom (сдвиг F2), а затем Trace (сдвиг F1), чтобы найти точка пересечения.
Еще проще использовать G-Solve (F5) и
затем функция пересечения ISCT (F5). Это дает нам первую точку зрения
пересечение. Затем нажимаем стрелку вправо, и калькулятор переходит к
вторая точка пересечения.
2-ln (B2)
Теперь выберите Инструменты а затем «Поиск цели» в строке меню.В на экране появляется следующее:
Пишем D2, 1 и B2 в промежутках, как показано. Мы просим Excel сделать значение ячейки D2 равным к значению 1, изменив значение в B2.
Когда нажимаем ОК, появляется следующая информация.
Это говорит нам о том, что аппроксимация x ≈ 0,45, которую мы нашли графически в примере 6, довольно хорошее решение x ≈ 0.4500289, найденный с помощью EXCEL, не намного лучше.
Попробуйте пройти тест 3 по уравнениям III.
Не забудьте использовать контрольный список для следите за своей работой.
График на числовой прямой
Построение графика на числовой прямой
Целые и действительные числа могут быть представлены в числовой строке . Точка на этой линии, связанная с каждым числом, называется графиком числа.
Обратите внимание на то, что числовые линии расположены одинаково или пропорционально (см. Рисунок 1).
Рисунок 1. Числовые линии.
График неравенств
При построении графиков неравенств, содержащих только целые числа, используются точки.
Пример 1
Изобразите набор x таким образом, чтобы 1 ≤ x ≤ 4 и x было целым числом (см. Рисунок 2).
{ x : 1 ≤ x ≤ 4, x — целое число}
Рисунок 2.График {x: 1 ≤ x ≤ 4, x является целым числом}.
При отображении неравенств с действительными числами используются линий, лучей и точек. Если номер указан, используется точка. Пустая точка используется, если номер не указан.
Пример 2
График, как показано (см. Рисунок 3).
Изобразите набор x таким образом, чтобы x ≥ 1.
{ x : x ≥ 1}
Изобразите набор x таким образом, чтобы x > 1 (см.
Рисунок 4).{ x: x > 1}
Изобразите набор x таким образом, чтобы x <4 (см. Рисунок 5).
{ x: x <4}
Рисунок 4).Этот луч часто называют открытым лучом или полупрямой . Пустая точка отличает открытый луч от луча.
Рис. 3. График { x : x ≥ 1}.
Рис. 4. График { x : x > 1}
Рисунок 5.График { x : x <4}
Интервалы
Интервал состоит из всех чисел, лежащих в двух определенных границах. Если включены две границы или фиксированные числа, то интервал называется закрытым интервалом . Если фиксированные числа не включены, то интервал называется открытым интервалом .
Пример 3
График.
Закрытый интервал (см. Рисунок 6).
{ x : –1 ≤ x ≤ 2}
Открытый интервал (см. Рисунок 7).
{ x: –2 < x <2}
Рис. 6. График, показывающий закрытый интервал { x : –1 ≤ x ≤ 2}.
Рис. 7. График, показывающий открытый интервал { x : –2 < x <2}.
Если интервал включает только одну из границ, то он называется полуоткрытым интервалом .
Пример 4
Постройте график полуоткрытого интервала (см. Рисунок 8).
{ x : –1 < x ≤ 2}
Рис. 8. График, показывающий полуоткрытый интервал { x : –1 < x ≤ 2}.
Что такое неравенство в математике?
Математика на крыльце>> Что такое неравенство? Введение в понимание и построение графиков неравенств
Введение в графическое отображение неравенств
Видео знакомит с тем, что такое неравенство.
Мы выясним, зачем нам нужны неравенства и как их построить.
Давайте продолжим эту идею, рассмотрев более тонкие детали построения графиков неравенств.
График: $ \ color {blue} {x <4} $
Начнем с графического представления некоторых чисел, которые делают утверждение $ x <4 $ истинным.
Это лишь некоторые из решений. Мы используем необходимость использовать линию, чтобы показать, что включены все числа меньше 4. Также, помещая открытый кружок в начало решения (около 4), мы говорим, что while $ 3.99999 $ — это часть набора решений, 4 — нет.
Когда число не входит в набор решений, кружок остается открытым.
График: $ \ color {blue} {x \ leq 4}
$ Мы снова воспользуемся линией, чтобы показать, что включены все числа меньше 4, но на этот раз мы поместим замкнутый круг (что означает, что мы закрашиваем круг) вокруг числа, где находится начало решения.
Итак, в этом случае закрашенный кружок вокруг 4 говорит читателю, что 4 является частью набора решений.
Когда число входит в набор решений, кружок закрашивается.
График: $ \ color {blue} {x> 4}
$ Выберите значение для x, чтобы определить, как нарисовать линию, представляющую набор решений. Поскольку 6 больше 4, линия рисуется вправо.
Когда число не входит в набор решений, кружок остается открытым.
Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet
Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию.График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение на графике, нанеся достаточно точек для распознавания шаблона, а затем соединить точки, чтобы включить все точки.
Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
Пример
Постройте функцию y = x + 2
Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.
| X | Y = х + 2 | Заказанная пара |
| -2 | -2 + 2 = 0 | (-2, 0) |
| -1 | -1 + 2 = 1 | (-1, 1) |
| 0 | 0 + 2 = 2 | (0, 2) |
| 1 | 1 + 2 = 3 | (1, 3) |
| 2 | 2 + 2 = 4 | (2, 4) |
Теперь вы можете просто построить пять упорядоченных пар в координатной плоскости
На данный момент это пример дискретной функции.
Дискретная функция состоит из изолированных точек.
Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.
Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения с y находится путем нахождения значения y, когда x = 0, (0, y).
Стандартная форма линейного уравнения —
$$ Ax + By = C, \: \: A, B \ neq 0 $$
Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы должны сначала решить уравнение относительно y.
$$ 2y-4x = 8 $$
$$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$
$$ 2y = 4x + 8 $$
$$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}}
$$$ y = 2x + 4 $$
Отсюда вы можете изобразить уравнение, как в примере выше.
Ваш комментарий будет первым