График уравнения онлайн: Построение графика функции онлайн

Онлайн-олимпиады и тесты по алгебре

• Главная /
• Олимпиады /
• По предметам и областям знаний /
• Математика /
• org/ListItem»> Алгебра

7 класс

• Арифметические операции над многочленами
• Арифметические операции над одночленами
• Базовые свойства степеней с натуральным показателем
• Взаимное расположение графиков линейных функций
• Деление многочлена на одночлен
• Деление одночленов
• Запись функции в виде y = f(x)
• Итоговый тест по математике (7 класс)
• Квадратичная функция y = x²
• Квадратичная функция и её график
• Координатная плоскость • Координаты точки
• Координатная прямая и числовые промежутки
• Линейная функция
• Линейная функция y = kx
• Линейная функция y = kx + m и её график
• Линейное уравнение с двумя переменными и его график
• Линейное уравнение с одной переменной
• Математические модели
• Математические модели реальных ситуаций
• Математический язык
• Основные понятия многочлена: теория и практика
• Понятие одночлена и его стандартный вид
• Понятие системы линейных уравнений с двумя переменными
• Понятие степени с натуральным показателем
• Понятие степени с нулевым показателем
• Произведение одночленов и возведение одночлена в степень
• Решение систем линейных уравнений методом подстановки
• Решение систем линейных уравнений методом сложения
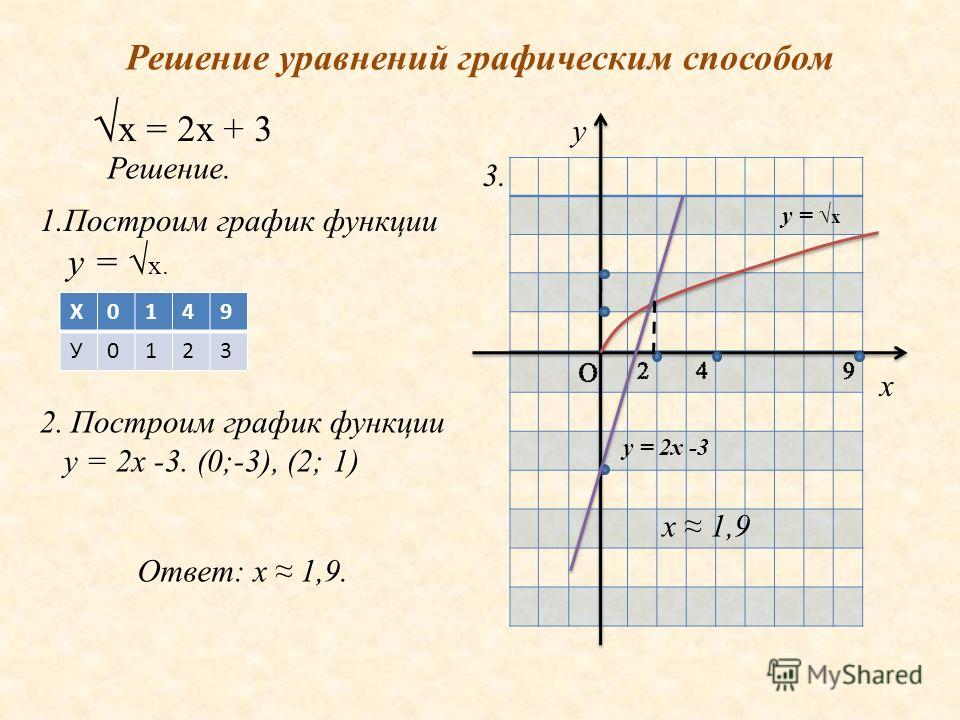
• Решение уравнений графическим методом
• Свойства степеней с натуральным показателем
• Системы линейных уравнений как математические модели реальных ситуаций
• Системы линейных уравнений с двумя переменными
• Сложение и вычитание многочленов
• Сложение и вычитание одночленов
• Таблица основных степеней (часто используемые степени)
• Умножение и деление степеней с одинаковыми натуральными показателями
• Умножение многочлена на многочлен
• Умножение многочлена на одночлен
• Формулы сокращённого умножения многочленов
• Числовые и алгебраические выражения

8 класс

• Базовые свойства квадратных корней
• Виды квадратных уравнений
• Действительные числа
• Иррациональные числа
• Итоговый тест по математике (8 класс)
• Квадратные уравнения
• Методы решения квадратных неравенств
• Множество рациональных чисел
• Модуль действительного числа и его геометрический смысл
• Монотонность функций
• Неравенства
• Понятие квадратного корня
• Преобразование иррациональных выражений
• Решение линейных неравенств
• Свойства числовых неравенств
• Способы решения квадратных уравнений
• Стандартный вид положительного числа
• Теорема Виета
• Функция y = |x| и функция квадратного корня y = √x
• Функция квадратного корня y = √x, её свойства и график
• Числовые промежутки

9 класс

• Арифметическая прогрессия
• Геометрическая прогрессия
• Итоговый тест по математике (9 класс)
• Комбинаторика • Статистика • Теория вероятностей
• Комбинаторные задачи
• Методы обработки информации (статистика)
• Методы решения систем рациональных уравнений
• Множества и подмножества • Объединение и пересечение множеств
• Неравенства и системы неравенств
• Определение числовой функции и способы её задания
• Понятие системы рациональных уравнений
• Простейшие вероятностные задачи
• Решение рациональных неравенств методом интервалов
• Свойства основных функций
• Системы рациональных неравенств
• Системы уравнений
• Системы уравнений как математические модели реальных ситуаций
• Способы решения линейных и квадратных неравенств
• Степенная функция с натуральным показателем
• Степенная функция с отрицательным целым показателем
• Функция кубического корня
• Чётные и нечётные функции • Определение чётности и нечётности
• Числовая последовательность
• Числовые последовательности и прогрессии
• Числовые функции и их свойства
• Экспериментальные данные и вероятности событий

10 класс

• Арккосинус и решение уравнения cos x = a
• Арксинус и решение уравнения sin x = a
• Арктангенс и арккотангенс • Решение уравнений tg x = a, ctg x = a
• Итоговый тест по математике (10 класс)
• Методы, используемые для решения тригонометрических уравнений
• Нахождение значений синуса и косинуса, тангенса и котангенса
• Обратимая и обратная функции
• Периодические функции
• Предел числовой последовательности
• Применение свойств функций к решению иррациональных уравнений
• Производная • Применение производной для исследования функций
• Тригонометрические уравнения
• Тригонометрические функции
• Тригонометрические функции углового аргумента
• Тригонометрические функции числового аргумента
• Числовые функции

11 класс

• Базовые свойства логарифмов
• Бином Ньютона и треугольник Паскаля
• Вероятность события
• Итоговый тест по математике (11 класс)
• Комбинаторика
• Комбинации событий
• Логарифмы • Показательная и логарифмическая функции
• Независимые события
• Определение логарифма, основное логарифмическое тождество
• Перестановки (комбинаторика)
• Правило произведения (комбинаторика)
• Правило суммы (комбинаторика)
• Размещения (комбинаторика)
• Сложение вероятностей
• Случайные события
• Сочетания и их свойства (комбинаторика)
• Статистическая вероятность
• Теория вероятностей

 

Mathpix — мобильное приложение, которое решает написанные от руки уравнения и строит по ним графики / Хабр

marks

000Z» title=»2016-05-17, 13:05″>17 мая 2016 в 13:05

Время на прочтение 1 мин

Количество просмотров

23K

Смартфоны Софт Лайфхаки для гиков

Это ПО — настоящий подарок для прилежных и нерадивых учащихся

Наверное, среди читателей Geektimes нет никого, кто хотя бы раз не писал от руки математическое уравнение. Ну, а строить графики уравнений — это обычное дело для любого школьника, студента или специалиста. Правда, на построение графика с использованием карандаша и линейки (и других подручных инструментов) требуется время, которого всегда мало.

Теперь появилось приложение, которое это время экономит. Встречаем Mathpix, которое сам разработчик называет «первой программой, которая может решать написанные от руки уравнения». Работает все очень просто: запускаем приложение, активируется камера телефона. Приложение фотографирует формулы, написанные на бумаге, и данные отправляются на сервер, где анализируются (на все про все уходят считанные секунды, судя по демонстрационному видео).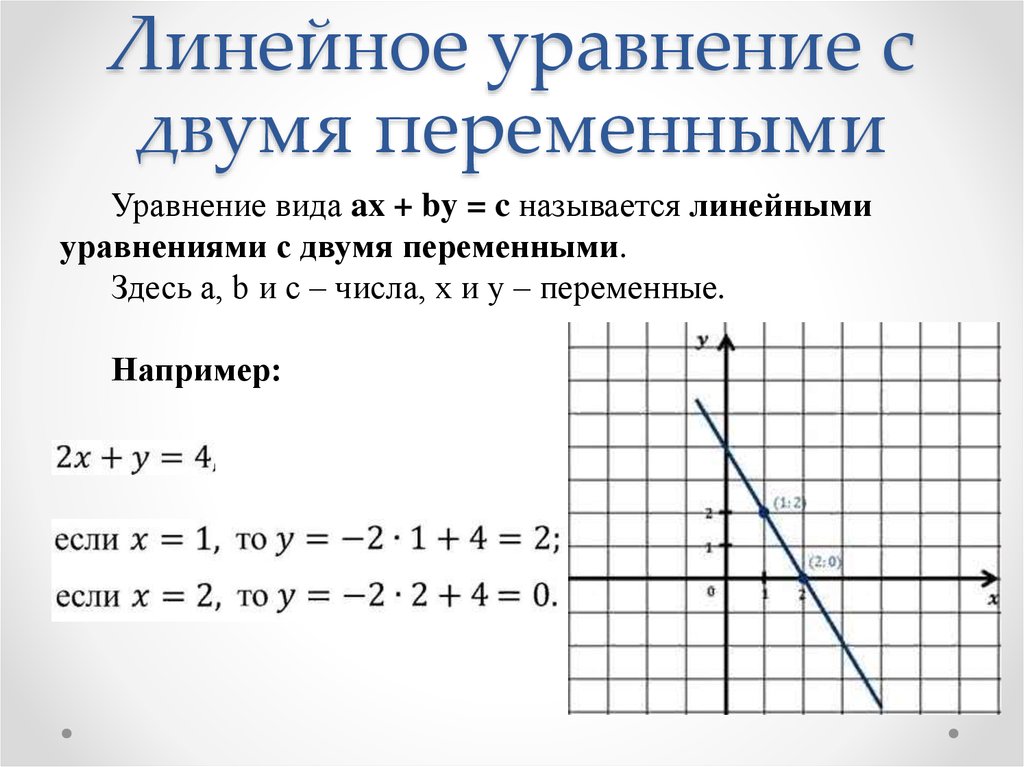 После анализа на экран выводятся инструменты для работы с уравнением — например, построение графика.

По словам Николаса Хименеса, разработчика приложения, в серверной части используются самообучающиеся алгоритмы, которые становятся все «умнее» с увеличением количества пользователей программы и количества проанализированных уравнений.

Использовать ПО можно для построения графиков уравнений, решения интегральных, тригонометрических уравнений. При этом выдается не только результат, но и промежуточные этапы решения.

Конечно, Хименес понимает, что ПО может использоваться недобросовестными учащимися школ и ВУЗов, но, по его словам, программа предназначена для помощи студентам, школьникам и специалистам в сложных ситуациях. При помощи Mathpix можно быстро прояснять для себя непонятные моменты в процессе решения уравнений, в ПО есть и обучающие моменты.

Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.

Как вы считаете, принесет ли пользу это приложение учащемуся?

33. 39% Да, конечно 198

48.23% Вероятно, но будут и желающие просто облегчить себе жизнь 286

18.04% Нет, это еще один инструмент оболванивания — ввел данные, и получил результат на тарелочке 107

0.34% Свое мнение, отпишусь в комментариях 2

Проголосовали 593 пользователя. Воздержались 94 пользователя.

Теги:

• математика
• смартфоны
• Mathpix

Хабы:

• Смартфоны
• Софт
• Лайфхаки для гиков

График линейных уравнений — MathCracker.com

Инструкции: Используйте этот Linear Equation Grapher для создания графика любого предоставленного вами линейного уравнения, показывающего все шаги. Вам нужно указать линейное уравнение, которое вы хотите построить в форме ниже.

Подробнее об этом графическом редакторе линейных уравнений

Рисование линий — фундаментальная способность, и этот калькулятор поможет вам в этом. Вам необходимо начать с предоставления линейное уравнение, которое вы хотите построить.

Вы можете указать любое линейное уравнение явно, например, x + 3y = 2 или что-то, что не полностью упрощено, как x + 3y = 2/3 x.

Линии графика имеют так много применений, что приобретать их становится очень практичным навыком. Геометрически линии имеют очень простую интуицию, которая позволяет легко график, так как нам не нужно много информации, чтобы указать их.

Как построить график линейных уравнений?

Вы можете использовать этот графический калькулятор для построения линий. Если вы решите сделать это вручную, вы должны знать, что этот подход требует преамбулы, которая будет зависеть от тип предоставляемой информации.

Каковы шаги для построения графика?

• Шаг 1: Определите тип предоставленной информации. У вас есть фактическое уравнение, у вас есть две точки, точка и наклон, наклон и y-пересечение? Четко оценить, что
• Шаг 2: Независимо от предоставленной информации, используйте ее, чтобы найти две точки, через которые проходит линия. Для заданного уравнения найдите y, например, для x = 0 и x = 1. Для наклона и y-перехвата вы составить уравнение y = a + bx и найти две точки. Если у вас есть одна точка и наклон, определите y = y1 + b(x-x1) и подставьте его на x = 0
• Шаг 3. Получив две точки, через которые проходит линия, используйте линейку, чтобы проследить линию, проходящую через них

Линии очень легко рисовать, просто вам нужно быть методичным и знать тип имеющейся у вас информации.

Даже если вы делаете это вручную, всегда приятно иметь удобный онлайн-калькулятор линейных графиков для проверки результатов.

Линии графика

Линии графика имеют множество применений. Например, вы можете решить систему уравнений, построив график соответствующие линии и увидеть, где они пересекаются.

Используя этот метод, когда прямые параллельны и не пересекаются, решений не будет.

Подобно тому, что произошло со сложением и вычитанием, деление дробей просто происходит от умножения дробей: Чтобы разделить две дроби, вы просто умножаете первый к обратная дробь второй (обратная дробь получается заменой числителя на знаменатель в дроби).

Другие применения линейных графиков

Линии или линейные графики действительно присутствуют повсюду. Линейные функции постоянно появляются в приложениях. в исчислении и оптимизации, поэтому они действительно полезно.

Пример: пример линейного графического уравнения

Нарисуйте следующие уравнения: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Решение: Нам нужно работать со следующим уравнением:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Сначала работаем с константами:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Результат получается путем размещения (y) слева и (x) и константы справа:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Затем процесс продолжается путем решения для \(y\), а затем путем деления обеих частей уравнения на \(\frac{7}{4}\). Получаем:

\[\ displaystyle y = — \ frac {\ frac {1} {2}} {\ frac {7} {4}} x \]

и после упрощения получается следующее.

\[\displaystyle y=-\frac{2}{7}x\]

Заключение : Мы делаем вывод, что уравнение линии в форме пересечения наклона, основанное на имеющихся данных, имеет вид \(\displaystyle y=-\frac{2}{7}x\) с наклон \(\displaystyle b = -\frac{2}{7}\) и y-пересечение \(\displaystyle n = 0\).

Следовательно, график представленной линии равен

Пример: Linear Equation Grapher пример

Получить строку, которая представляет: \(\frac{2}{3}x + \frac{5}{4}y = — \frac{5}{6}x + 2\)

Решение: Мы получили следующее уравнение:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Работа с константами:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Теперь, подставив \(y\) в левую часть, а \(x\) и константу в правую, мы получим

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Теперь член, умножающий \(y\), равен \( \frac{5}{4} — 0 = \frac{5}{4}\), а также поскольку \( -\frac{5}{6 } — \frac{2}{3} = -\frac{3}{2}\), получается следующее

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Теперь, найдя \(y\), разделив обе части уравнения на \(\frac{5}{4}\), получим следующее

\[\ displaystyle y = — \ frac {\ frac {3} {2}} {\ frac {5} {4}} x + \ frac {2} {\ frac {5} {4}} \]

и упрощая окончательно получаем следующее

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Заключение : На основании предоставленных данных мы заключаем, что уравнение линии в форме наклона-пересечения имеет вид \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5} \), с наклоном \(\displaystyle b = -\frac{6}{5}\) и пересечением по оси Y \(\displaystyle n = \frac{8}{5}\).

Линейный график

Другие линейные калькуляторы

Линии настолько важны, что заслуживают отдельного раздела в учебнике по математике. Вы можете вычислять линейные уравнения в различных формах, в зависимости от конкретные потребности.

Для определения линий в конечном итоге потребуются две точки, через которые проходит линия, которые можно указать прямо или косвенно.

Графический калькулятор линейных уравнений | Бесплатный онлайн калькулятор линейных уравнений с шагами

Онлайн калькулятор линейных уравнений

Как пользоваться калькулятором графиков линейных уравнений?

1. Начните с ввода линейного уравнения в данное поле ввода.
2. Нажмите «Решить», чтобы получить результат.
3. Наконец, в поле вывода будут отображены точки пересечения x и y уравнения.
4. Вы можете установить флажок «Показать шаги», чтобы понять, какие шаги нужно выполнить, чтобы получить ответ.
5. Проанализируйте график, чтобы понять, как были нанесены координаты.
6. Также узнайте больше, нажав «Пример», чтобы просмотреть различные уравнения и соответствующие им графики.

Что такое линейное уравнение?

Линейное уравнение определяется как уравнение со степенью один. Когда это уравнение изображено на графике, мы видим, что оно всегда будет иметь форму прямой линии.

Что такое линейное уравнение с одной переменной?

Линейное уравнение с одной переменной является уравнением с одной переменной. Ax + B = 0 — стандартная форма линейного уравнения с одной переменной, где x — переменная, A — ее коэффициент, а B — константа в этом уравнении.

Что такое линейное уравнение с двумя переменными?

Уравнение с двумя переменными называется линейным уравнением с двумя переменными. Линейное уравнение с двумя переменными, записанное в стандартной форме, имеет вид Ax + By = C, где x и y — переменные, A и B — коэффициенты, а C — константа.

Какое решение уравнения? Как они представлены на графике?

Решение — это значение или набор значений, при подстановке которых неизвестное делает уравнение верным.

Каждое значение или набор значений будет действовать как точка на линии графика. Это означает, что каждая упорядоченная пара этой линии является решением уравнения.

Что такое x-intercept?

Координата x точки, в которой линия пересекает ось x, является точкой пересечения x. На оси x нет координаты y. Следовательно, чтобы найти точку пересечения x уравнения без рисования графика, нам просто нужно заменить значение y на ноль, полученное значение x будет точкой пересечения x.

Решенные примеры

Пример 1: Решите уравнение 3x + 9 = 0

 

Решение: значений
Шаг 1: 90 таблица из 86.

 

 

Шаг 2: Постройте упорядоченные пары.

Шаг 3: Теперь через эти точки проведите прямую линию.

 

 

Пример 2. Нарисуйте график для y = 2x + 4

Решение:

Шаг 1: Составьте таблицу значений.

 

 

Шаг 2: Постройте упорядоченные пары.

Шаг 3: Теперь через эти точки проведите прямую линию.

 

Часто задаваемые вопросы

Что такое уравнение?

Математическое выражение, содержащее символ равенства, называется уравнением.

Что такое y-перехват?

Когда линия пересекает другую линию, мы получаем точку пересечения. Таким образом, когда линия пересекает ось Y, мы получаем точку пересечения. Координата y этой точки называется точкой пересечения с осью y.

Можно ли решить уравнение, содержащее две переменные, одним уравнением?

Чтобы решить для всех переменных, нам нужно равное количество уравнений в качестве переменных. Таким образом, мы не можем решить уравнение с двумя переменными, используя только одно уравнение.