Задачи на степенные функции 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Функции натуральные числа, их свойства и графики
Урок: Задачи на степенные функции
1. Введение
На этом уроке мы вспомним свойства степенных функций, т. е. функций вида , где – натуральное число, и решим серию типовых задач.
2. Функция
Рассмотрим степенную функцию с четным показателем степени (рис. 1).
3.Функция четная, т.е.
4. Всё семейство функций проходит через три фиксированные точки:
5. Функция не монотонна на всей области определения: функция убывает при ; функция возрастает при
3. Примеры
1. Отметим интервалы знакопостоянства функции на примере функции (рис. 2).
2. Рассмотрим функцию и ее интервалы знакопостоянства (рис. 3).
Рассмотрим функцию и ее интервалы знакопостоянства (рис. 3).
Рассмотрим задачу с параметром:
Найти число корней уравнения
Решение:
Метод решения подобных задач следующий:
1. Изобразить график функции.
2. Пересечь график семейством прямых
3. Определить число точек пересечения и выписать ответ (рис. 4).
При корней нет;
при уравнение имеет один корень;
при уравнение имеет два корня. Заметим, что сумма этих корней равна нулю.
4. Функция
Теперь кратко повторим график и свойства степенной функции с нечетным показателем.
Функция (рис. 5).
1.
2.
3. Функция нечетная, т.е. График симметричен относительно точки (0; 0).
4. Любая из функций проходит через три фиксированные характерные точки:
5. Функция монотонно возрастает.
5. Решение задач с использованием свойств степенных функций
Рассмотрим примеры.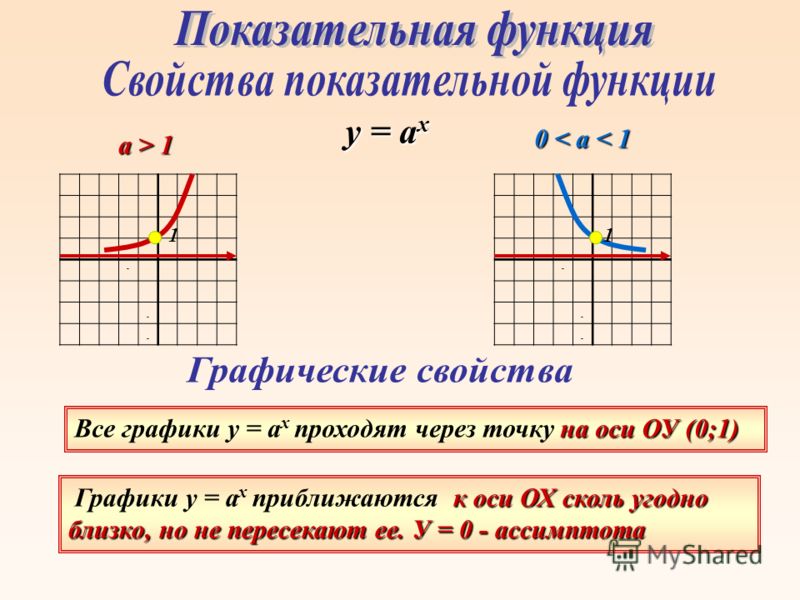
1. Найти область значений функции и прочитать её график.
Решение:
При y убывает,
При y возрастает,
Ответ:
При функция возрастает,
Ответ:
2. Найдите точки пересечения графиков функций:
Решение:
Графики функций пересекаются в точках
Ответ:
Графики функций пересекаются в точках
Ответ:
3. Постройте и прочитайте график функции
Решение:
Еслито yубывает,
Если то yвозрастает,
Если то у убывает,
На примере предыдущей функции рассмотрим важную сопутствующую задачу.
Найти число корней уравнения с параметром:
Решение:
Решить уравнение с параметром означает перебрать все возможные значения параметра и для каждого указать ответ.
Методика решения таких задач нам известна:
1. Построить график функции .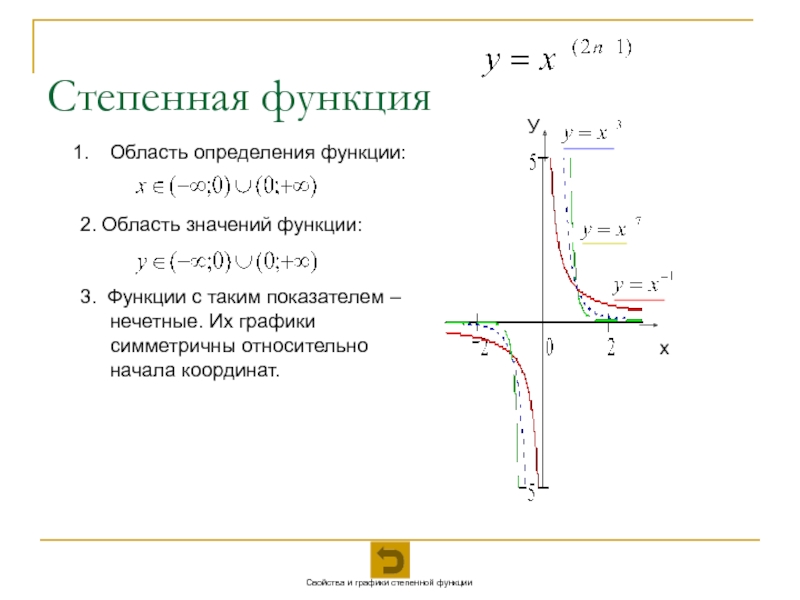
2. Пересечь его семейством прямых.
3. Найти точки пересечения и выписать ответ (рис. 11).
Нет корней при .
Один корень при.
Два корня при.
Три корня при
6. Заключение
Мы вспомнили основные свойства степенных функций с натуральным показателем и решили серию типовых задач. На следующем уроке мы расcмотрим функцию
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на ресуры интернет
1. Открытая математика (Источник).
2. Задачи (Источник).
3. Решу ЕГЭ (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№311, 312, 321.
Степенная функция, ее свойства и графики – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Степенной функцией называют функцию \(y=x^n\), где \(n\) – любое действительное число, отличное от нуля.
Свойства степенной функции с нечетным положительным показателем
- Область определения: \(D(y)=(-\infty;+\infty)\).
- Область значений: \(E(y)=(-\infty;+\infty)\).
- Функция нечетная, так как \(y(-x)=-y(x)\).
- Функция возрастает при \(x\in (-\infty;+\infty)\).
- Функция выпуклая при \(x\in (-\infty;0]\) и вогнутая при \(x\in [0;+\infty)\) (кроме линейной функции).
- Точка \((0; 0)\) является точкой перегиба (кроме линейной функции).
- Асимптот нет.
- Функция проходит через точки \((-1; -1), (0; 0), (1; 1)\).
Свойства степенной функции с четным положительным показателем
- Область определения: \(D(y)=(-\infty;+\infty)\).
- Область значений: \(E(y)=[0;+\infty)\).
- Функция четная, так как \(y(-x)=y(x)\).
- Функция возрастает при \(x\in[0;+\infty)\), убывает при \(x\in(-\infty;0]\).
- Функция вогнутая при \(x\in (-\infty;+\infty)\).

- Точек перегиба нет.
- Асимптот нет.
- Функция проходит через точки \((-1; 1), (0; 0), (1; 1)\).
Свойства степенной функции с нечетным отрицательным показателем
- Область определения: \(D(y)=(-\infty;0)\cup(0;+\infty)\).
- Область значений: \(E(y)=(-\infty;0)\cup(0;+\infty)\).
- Функция нечетная, так как \(y(-x)=-y(x)\).
- Функция убывает при \(x\in(-\infty;0)\cup (0;+\infty)\).
- Функция выпуклая при \(x\in(-\infty;0)\) и вогнутая при \(x\in(0;+\infty)\).
- Точек перегиба нет.
- Горизонтальной асимптотой является прямая \(y = 0\).
- Функция проходит через точки \((-1;-1), (1;1)\).
Свойства степенной функции с четным отрицательным показателем
- Область определения: \(D(y)=(-\infty;0)\cup(0;+\infty)\).
- Область значений: \(E(y)=(0;+\infty)\).
- Функция четная, так как \(y(-x)=y(x)\).
 4}\), где \(x\in[2;3)\).
4}\), где \(x\in[2;3)\). - Введите время и значения функция
- Введите значения второй функции и их относительное время
- Введите точку для оценки (необязательно)
- Нажмите кнопку расчета
- Пошаговый расчет показательной функции
- Графическое представление экспоненциального роста и затухания
Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот Объем файла не должен превышать 1МБКазахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
Сканируй QR код, скачивай приложение
и учись вместе с нами
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Экспоненциальная функция Графический редактор — MathCracker.com
Решатели Статистика
9{rt}\).
 {kt}\]
{kt}\]Для того, чтобы получить график, вам просто нужно указать параметры \(A_0\) и \(k\) для одной или двух функций (в зависимости от того, хотите ли вы построить график одной функции или хотите сравнить две функции).
Но как найти экспоненциальную функцию по точкам?
Технически, чтобы найти параметры, нужно решить следующую систему уравнений: 9{к т_2}} \]
Как построить график экспоненциальной функции
Экспоненциальная функция указанного выше вида будет иметь характерный экспоненциальный вид, и ее общий вид будет зависеть от того, положительна или отрицательна скорость \(r\).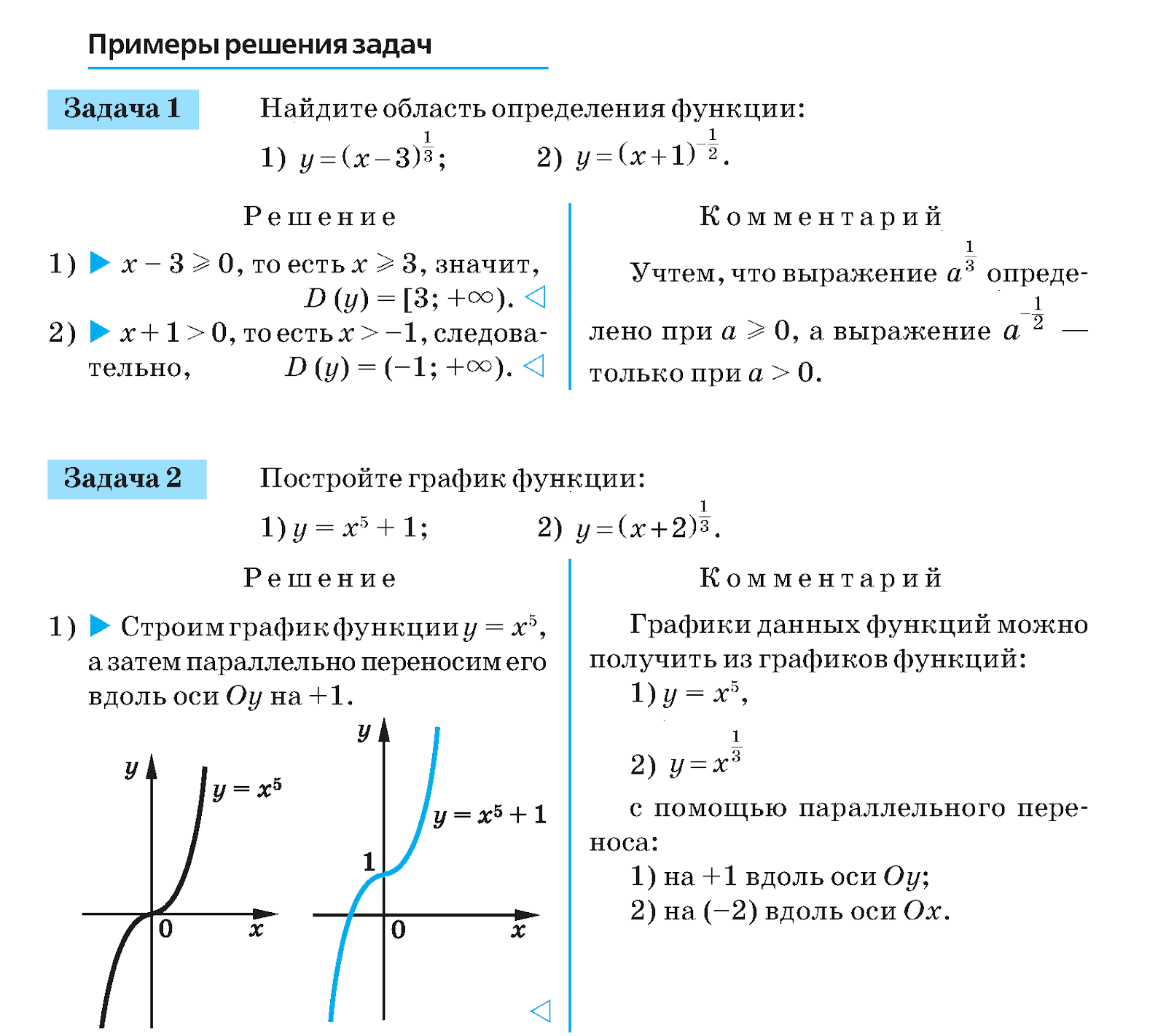
Для положительной скорости \(r\) мы будем иметь экспоненциальный рост , а для отрицательной скорости \(r\) будем иметь экспоненциальный спад .
Каковы основные характеристики экспоненциальных графиков?
Они имеют очень специфическую форму, так как растут или распадаются (в зависимости от знака \(r\)) очень быстро. Типов графиков в этом случае не так много. Только быстрый (экспоненциальный) спад или быстрый (экспоненциальный) рост.
Базовый пакет статистики
Экспоненциальный калькулятор вероятности
Экспоненциальный калькулятор вероятности онлайн
Калькулятор вероятности
Вероятностный решатель
Решатель статистики
9kt, как известно, является показательной функцией.
Рассмотрим две функции (y1, y2) и их соответствующие значения (4, 5) в относительное время (2,5). Мы хотим оценить их поведение в момент времени t = 5,9.{0,0744×5}$$
$$ f\left(5\right) = 5 $$
Вы можете использовать калькулятор экспоненциального уравнения для проверки результатов за считанные секунды.
Окончательный график:Работа калькулятора экспоненциальной функции:
Использование этого калькулятора формул экспоненциальной функции требует следующих входных данных для расчета результатов:
Ввод: 9000 7
Вывод:
Экспоненциальные функции имеют два типа: экспоненциальный рост и экспоненциальное затухание.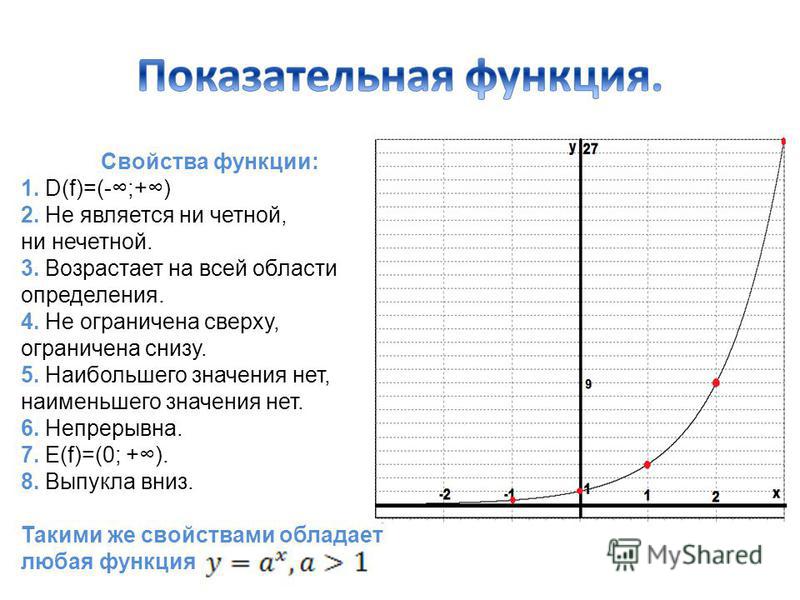

 4}\), где \(x\in[2;3)\).
4}\), где \(x\in[2;3)\).
Ваш комментарий будет первым