Система 2×2 линейных уравнений — Онлайн Solver
Алгебра Рельефы
инструкции Этот инструмент он находит решения для системы двух одновременных линейных уравнений с двумя переменными.Способ, используемый для решения уравнения, — это метод Крамера.Пожалуйста, заполните форму ниже с параметрами для обоих линейных уравнений:
Введите 1-е линейное уравнение (например, 2x + 3Y = 4)
 X — 3Y = 2)
X — 3Y = 2) Этот калькулятор позволяет решить два одновременных линейных уравнения, с двумя переменными, которые часто называют «двух-дшими системами». Эти виды 2×2 систем очень часто используются в алгебре, потому что они часто появляются во всех видах приложений, как когда вы Попробуйте решить слова проблемы.
Как правило, переменные, используемые в двухподневой линейной системе, называются по умолчанию \(x\) и \(y\), но это только конвенция, как они могут быть \(u\) и \(v\) Если вы хотите
Итак, это система дву- две:
\[x + 2y = 4\] \[2x — 2y = 2\]
так же, как это
\[2u — 2v = 1\] \[u — 3v = 2\]
это двух- две системы.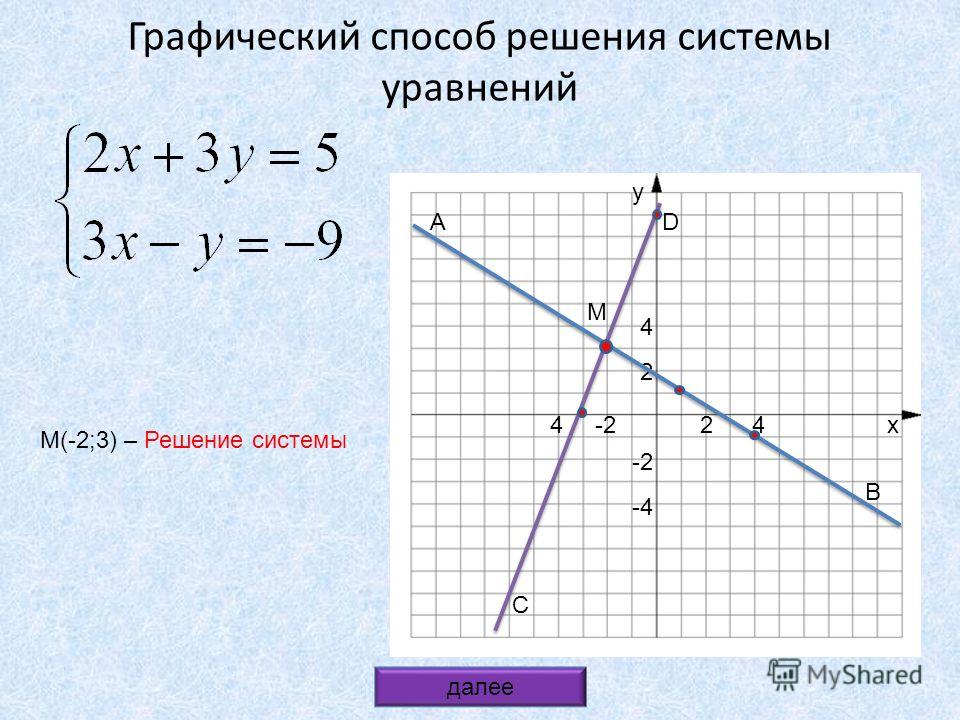 Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
Важно то, что у нас есть два линейных уравнения с двумя переменными (неизвестными)
Методы решения линейных систем 2×2
К счастью, есть много способов использовать для решения двухгибовых систем, и у вас есть преимущество, чтобы выбрать, какой метод использовать. Наиболее часто используемыми методами являются:
- График
- Замена
- Ликвидация
Метод графики основан на, нет удивлению, график двух уравнений и пытаясь визуально определить, где эти две линии пересекаются (если они пересекаются
вообще).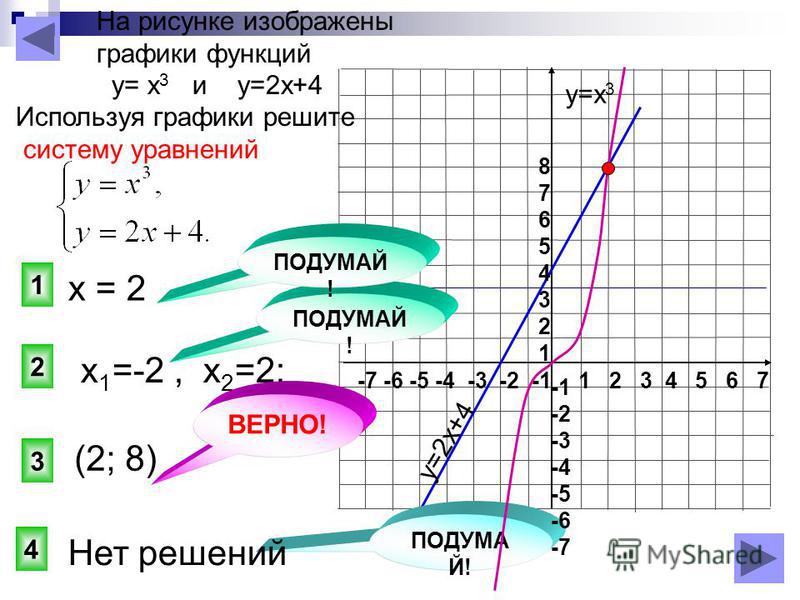 Этот метод естественным образом ограничивает приближения в большинстве случаев
Этот метод естественным образом ограничивает приближения в большинстве случаев
Метод замены основан на идее, которую можно решить для одной переменной в одном из уравнений, а затем подключить, что в другое уравнение, для решения для другой переменной.Часто это удобно, потому что структура одного из уравнений может привести к нему решить для одной переменной. Но это не всегда так, и этот метод в значительной степени ограничен случаем систем 2×2
Метод ликвидации основан на идее, которую можно манипулировать одному или оба уравнения, чтобы получить их или вычесть их, так что одна переменная исчезает. В некотором смысле,
Это более общий способ использования метода замещения
В некотором смысле,
Это более общий способ использования метода замещения
Как бороться с большими системами линейных уравнений?
Три метода, представленные выше, действительно могут быть эффективно использованы только с системами 2×2, что и для больших систем, которые системы становятся гораздо более сложными и Может быть, даже возможно использовать эти методы
Для 3×3 и крупных систем лучше всего использовать систематические подходы, такие как использование
МЕТОД КРАМЕРА
Для общего \(n \times n\) системы или используя
ГАУСОВСКАЯ ЛИКВИДАЦИЯ.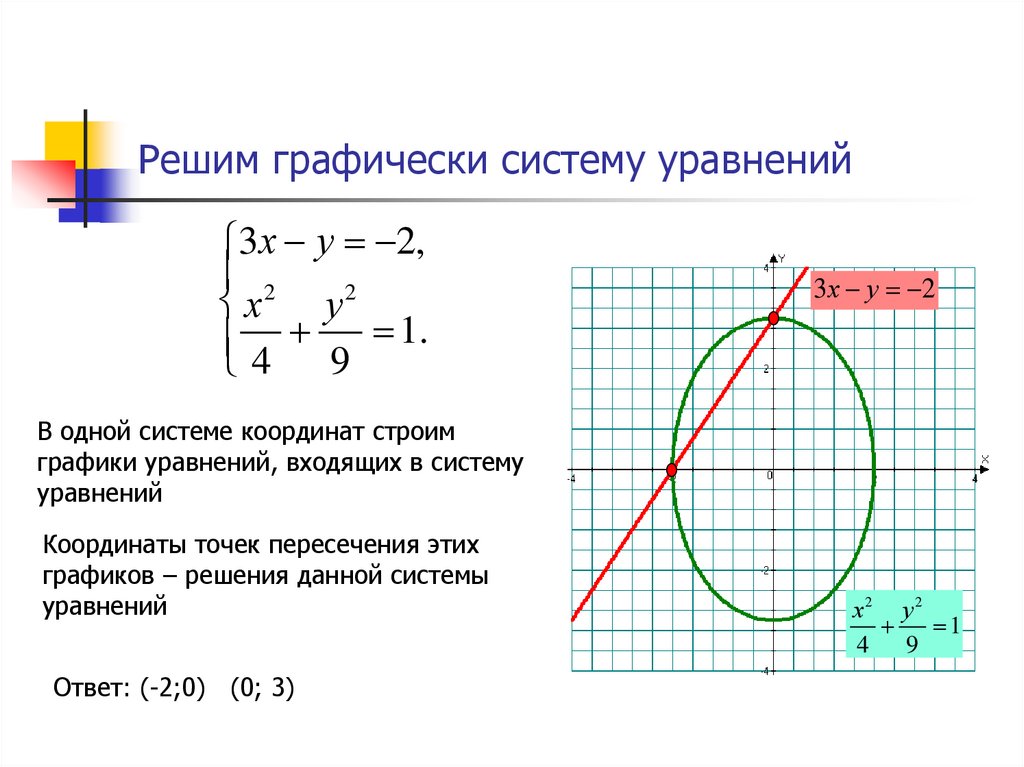
Алгебра калькулятор Алгебра калькулятор онлайн Алгебра Рельвер Система уравнений 2×2 Система 2×2 линейных уравнений калькулятора
Графический метод решения системы уравнений 9 класс онлайн-подготовка на Ростелеком Лицей
Тема: Системы уравнений
Урок: Графический метод решения системы уравнений
1.
 Тема урока, основные определения
Тема урока, основные определения
Рассмотрим систему
Пару чисел которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.
Решить систему уравнений – это значит найти все её решения, или установить, что решений нет. Мы рассмотрели графики основных уравнений, перейдем к рассмотрению систем.
2. Решение линейной системы уравнений
Пример 1. Решить систему
Решение:
Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений (Рис. 1).
Решением системы является пара чисел Подставив эту пару чисел в каждое уравнение, получим верное равенство.
Мы получили единственное решение линейной системы.
Ответ:
Вспомним, что при решении линейной системы возможны следующие случаи:
cистема имеет единственное решение – прямые пересекаются,
система не имеет решений – прямые параллельны,
система имеет бесчисленное множество решений – прямые совпадают.
Мы рассмотрели частный случай системы, когда p(x; y) и q(x; y) – линейные выражения от x и y.
3. Решение нелинейных систем уравнений
Пример 2. Решить систему уравнений
Решение:
График первого уравнения – прямая, график второго уравнения – окружность. Построим первый график по точкам (Рис. 2).
|
x |
|
-1 |
|
y |
1 |
0 |
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в т. А(0; 1) и т. В(-1; 0).
Ответ:
Пример 3. Решить систему графически
Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 2. График второго уравнения – парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина – точка (0; 2) (Рис. 3).
График второго уравнения – парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина – точка (0; 2) (Рис. 3).
Графики имеют одну общую точку – т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.
Ответ:
Пример 4. Решить систему
Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 1 (Рис. 4).
Построим график функции Это ломаная (Рис. 5).
Теперь сдвинем ее на 1 вниз по оси oy. Это и будет график функции
Поместим оба графика в одну систему координат (Рис. 6).
Получаем три точки пересечения – т. А(1; 0), т. В(-1; 0), т. С(0; -1).
Ответ:
4. Заключение, вывод
Мы рассмотрели графический метод решения систем. Если можно построить график каждого уравнения и найти координаты точек пересечения, то этого метода вполне достаточно.
Но часто графический метод даёт возможность найти только приближенное решение системы или ответить на вопрос о количестве решений. Поэтому нужны и другие методы, более точные, и ими мы займемся на следующих уроках.
Поэтому нужны и другие методы, более точные, и ими мы займемся на следующих уроках.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А.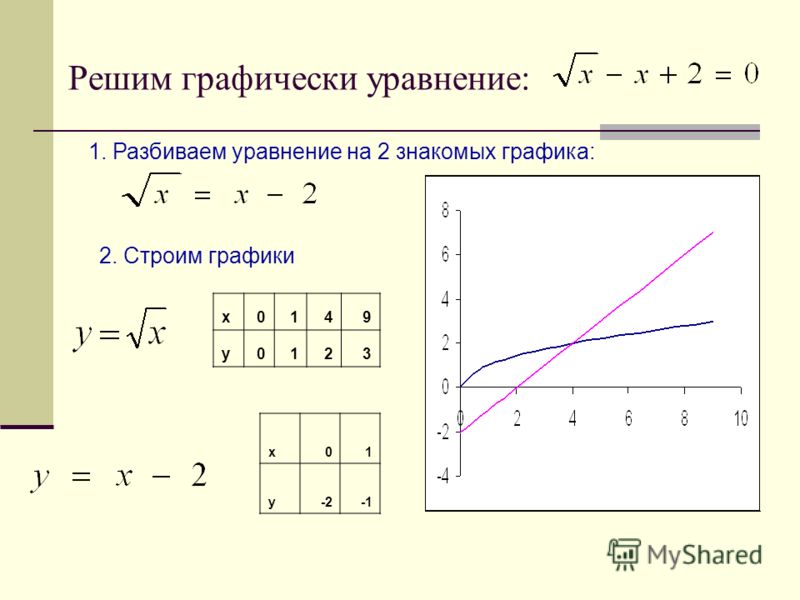 Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 105, 107, 114, 115.
Калькулятор метода построения системы уравнений
Решатели Алгебра Калькуляторы
Инструкции: Используйте этот калькулятор для решения системы двух линейных уравнений графическим методом.
Введите линейное уравнение (пример: y = 2x + 3, 3x — 2y = 3 + 2/3 x и т. д.)
Введите другое линейное уравнение (пример: y = 2x + 3, 3x — 2y = 3 + 2/3 x и т. д.)
(необязательно) Минимум x =
(необязательно) Максимум x =
Системы линейных уравнений очень часто встречаются в различном контексте алгебры. Наиболее часто встречающиеся системы в базовых курсах алгебры представляют собой системы 2 на 2, которые состоят из двух прямых уравнений и двух переменных.
Такие системы «два на два» часто появляются при решении задач со словами, задач на пропорции и задач на присваивание с ограничением.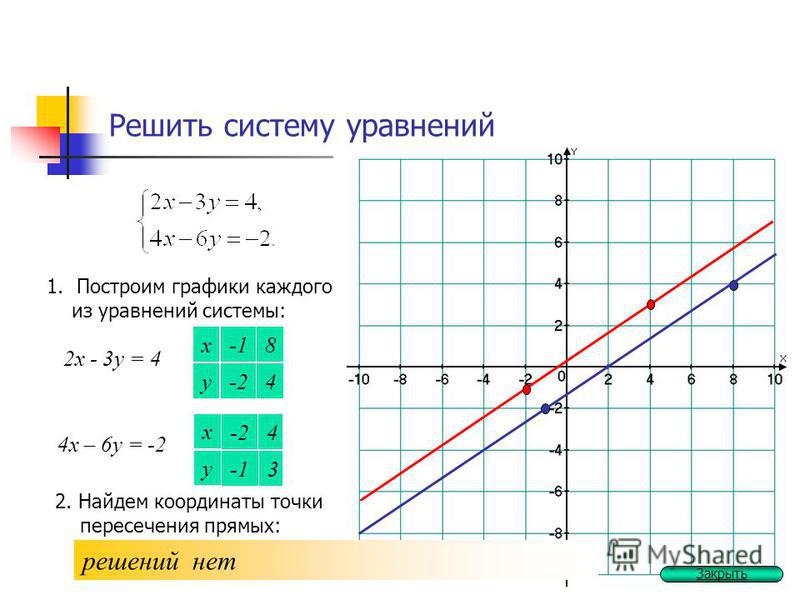 Естественно, крупнее
системы (с большим количеством переменных и уравнений) также распространены, здесь сосредоточьтесь только на системах 2×2, потому что их мы можем изобразить графически.
Естественно, крупнее
системы (с большим количеством переменных и уравнений) также распространены, здесь сосредоточьтесь только на системах 2×2, потому что их мы можем изобразить графически.
Как пользоваться графическим методом
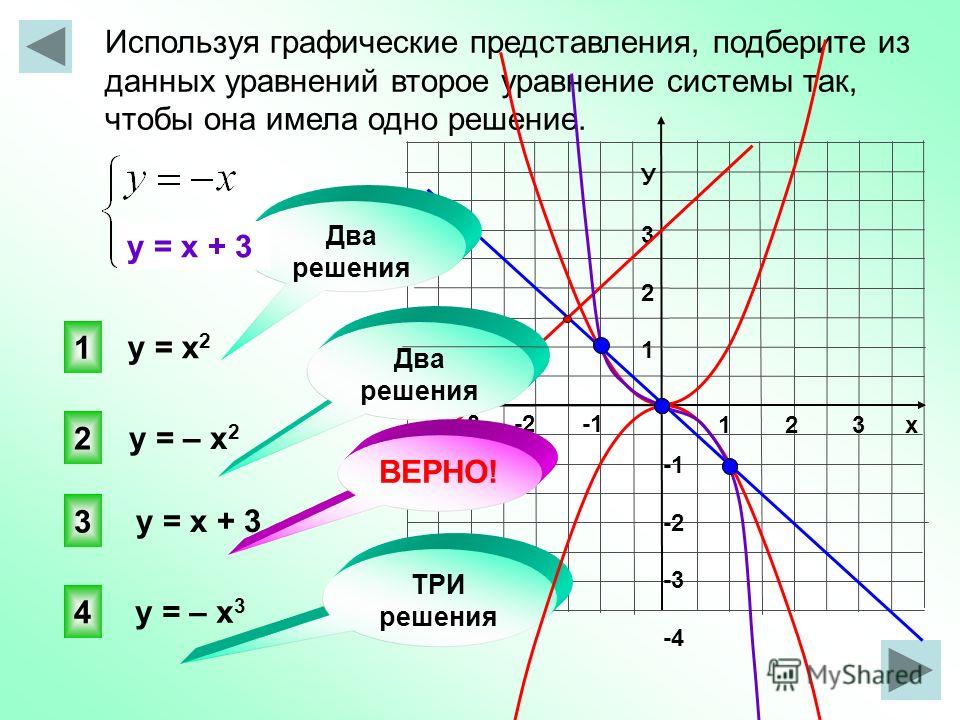
Графический метод состоит в представлении каждого из линейных уравнений в виде линии на графике. Затем нам нужно найти пересечение точки между двумя линиями, используя наблюдение, что точка пересечения линии (если она существует) будет решением системы.
Что произойдет, если перекрестка не существует? Это было бы в том случае, если бы линии были параллельны, но не были бы одной и той же линией, и в этом случае нет пересечение. Правило понятно: когда между линиями нет пересечения, у системы нет решения.
Возможен и третий случай: линии могут быть параллельны, но на самом деле идентичны (это одна и та же линия). Итак, сколько перекрестков
баллы у тебя есть? Да, вы правы: у вас бесконечные точки пересечения, а значит, у вас есть бесконечные решения.
Итак, сколько перекрестков
баллы у тебя есть? Да, вы правы: у вас бесконечные точки пересечения, а значит, у вас есть бесконечные решения.
Решение систем уравнений путем графического отображения ответов
Итак, методология проста: вы начинаете с линейной системы, и первое, что вы делаете, это графически изображаете два линейные уравнения.
Затем вы смотрите на график и оцениваете, пересекаются ли линии только в одной точке (что происходит, если линии имеют разные наклоны, и в этом случае у вас есть уникальное решение.
Если нет, посмотрите, параллельны ли они и различны, и в этом случае решений нет. В противном случае, если два прямые равны, то у нас есть бесконечные решения.
Как решить систему уравнений на графическом калькуляторе?
Все системы работают по-разному. В этом случае с этим графическим калькулятором все, что вам нужно сделать, это ввести два линейных уравнения, даже если они
не совсем упрощенный.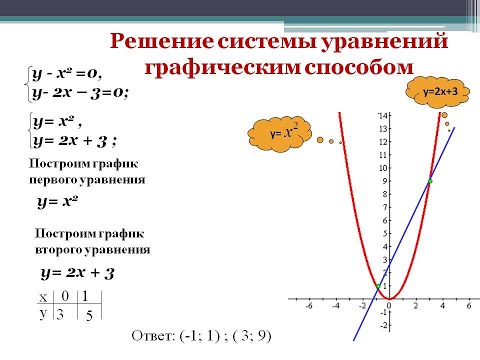 Калькулятор сначала попытается перевести линии в точку пересечения наклона и предоставит вам график и
приближенная оценка решения.
Калькулятор сначала попытается перевести линии в точку пересечения наклона и предоставит вам график и
приближенная оценка решения.
Разные калькуляторы дают разные результаты, но большое преимущество этого калькулятора в том, что он обеспечивает все этапы процесса.
Как вы пишете системы уравнений из графика?
Линейные функции однозначно связаны. То есть одно линейное уравнение связано только с одной и одной прямой, и наоборот, линия связаны только с одним линейным уравнением и одним линейным уравнением.
Итак, чтобы написать системы уравнений с графика, нужно работать с каждой строкой отдельно. Возьмите одну линию и определите две точки на линия. С этими двумя точками вы можете вычислить наклон линии.
Затем, с учетом наклона линии и точки пересечения с осью Y,
вы можете написать уравнение линии в форме пересечения наклона.
Метод построения системы уравнений калькулятор системы линейных уравнений калькулятор решения уравнения системы s
Решатель систем уравнений: Wolfram|Alpha
О, о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
WolframAlpha
Решение уравнений и систем уравнений с помощью Wolfram|Alpha
Мощный инструмент для поиска решений систем уравнений и ограничений
Wolfram|Alpha способен решать самые разные системы уравнений. Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, и может специально искать целочисленные решения или решения в другой области. Кроме того, он может решать системы, включающие неравенства и более общие ограничения. 92 = 4, y = x
Кроме того, он может решать системы, включающие неравенства и более общие ограничения. 92 = 4, y = x
- Посмотреть другие примеры »
Доступ к инструментам мгновенного обучения
Немедленная обратная связь и руководство с помощью пошаговых решений и Генератора проблем Wolfram
Узнайте больше о:
- Шаг пошаговые решения »
- Генератор задач Wolfram »
Что такое системы уравнений?
Система уравнений представляет собой набор из одного или нескольких уравнений, включающих ряд переменных.
Решениями систем уравнений являются такие отображения переменных, что удовлетворяются все уравнения компонентов, другими словами, места, в которых все эти уравнения пересекаются. Решить систему значит найти все такие общие решения или точки пересечения.
Системы линейных уравнений — распространенное и применимое подмножество систем уравнений. В случае двух переменных эти системы можно рассматривать как линии, проведенные в двумерном пространстве. Если все прямые сходятся в одной точке, то говорят, что система непротиворечива и имеет решение в этой точке пересечения. В противном случае система называется несовместной, не имеющей решений. Системы линейных уравнений с более чем двумя переменными работают аналогично, имея либо одно решение, либо отсутствие решений, либо бесконечное количество решений (последнее в случае, если все уравнения компонентов эквивалентны).
Если все прямые сходятся в одной точке, то говорят, что система непротиворечива и имеет решение в этой точке пересечения. В противном случае система называется несовместной, не имеющей решений. Системы линейных уравнений с более чем двумя переменными работают аналогично, имея либо одно решение, либо отсутствие решений, либо бесконечное количество решений (последнее в случае, если все уравнения компонентов эквивалентны).
Возможны и более общие системы, включающие нелинейные функции. Они обладают более сложными наборами решений, включающими одно, нулевое, бесконечное или любое количество решений, но работают аналогично линейным системам в том смысле, что их решениями являются точки, удовлетворяющие всем задействованным уравнениям. Идя дальше, возможны более общие системы ограничений, например, включающие неравенства или требующие, чтобы определенные переменные были целыми числами.
Решение систем уравнений является очень общей и важной идеей, которая является фундаментальной во многих областях математики, техники и естественных наук.
Ваш комментарий будет первым