ОТРИЦАТЕЛЬНЫЕ ЗНАЧЕНИЯ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если у мы знаем функцию f(x) и нам нужно построить функцию f(–x) (то есть заменить все иксы в функции на противоположные), тогда нужно отразить график симметрично относительно оси Оу, т.е. все ординаты останутся неизменными, а абсциссы поменяют знак.
Например:
Четная функция при таком изменении не изменяется, т.к. это следует из определения четной функции.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если у мы знаем функцию f(x) и нам нужно построить функцию –f(x) (то есть заменить все значения функции на противоположные), тогда нужно отразить график симметрично относительно оси Ох, т.е. все абсциссы останутся неизменными, а ординаты поменяют знак.
ИЗМЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(x)\ \pm \ a\ \)(то есть прибавить к получившимся значениям функции \(\pm\) a), тогда f(x) будет двигаться по оси Оу.
– Если нужно построить \(f(x)\ + \ a\), то функция поднимется на a единичных отрезков вверх.
– Если нужно построить \(f(x)\ –\ a\), то функция опуститься на a единичных отрезков вниз.
Например:
Функция \(y = \frac{1}{x} + 5\) будет выше функции \(y = \frac{1}{x}\) на 5 единичных отрезков, а функция \(\frac{1}{x}\ –\ 4\) ниже на 4 единичных отрезка:
ПРОИЗВЕДЕНИЕ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить функцию \(f(\text{ax})\ \)(то есть заменяем все иксы на выражение ax), тогда функция \(f(x)\) будет «сжиматься» и «растягиваться» вдоль оси Ох.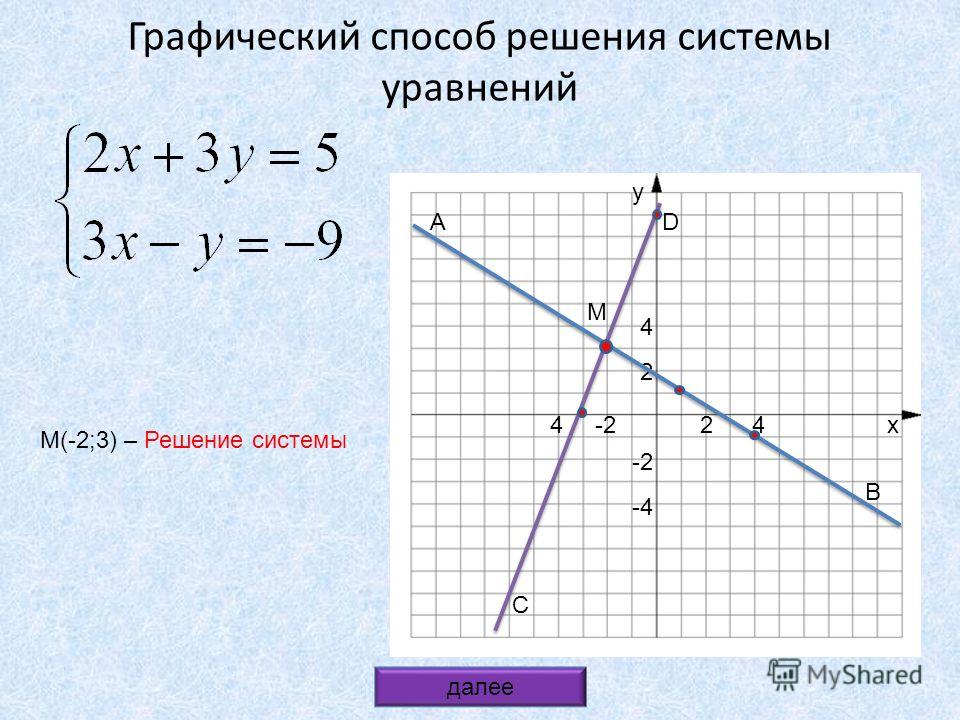
МОДУЛЬ:
ИЗМЕНЕНИЕ АРГУМЕНТА
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(f(|x|)\) (то есть заменяем все иксы на модуль икс), тогда график в области с отрицательными абсциссами стирается, а график в области с положительными абсциссами отражается относительно оси Оу. Функция становится четной.
Например:
ИЗЕНЕНИЕ ЗНАЧЕНИЯ ФУНКЦИИ
Если мы знаем функцию \(f(x),\) а нам нужно построить график функции \(|f\left( x \right)|\) (то есть берем под модуль значение функции). Тогда график в области с отрицательными ординатами отражается относительно оси Ох.
Например:
график дифференциального уравнения онлайн
график дифференциального уравнения онлайн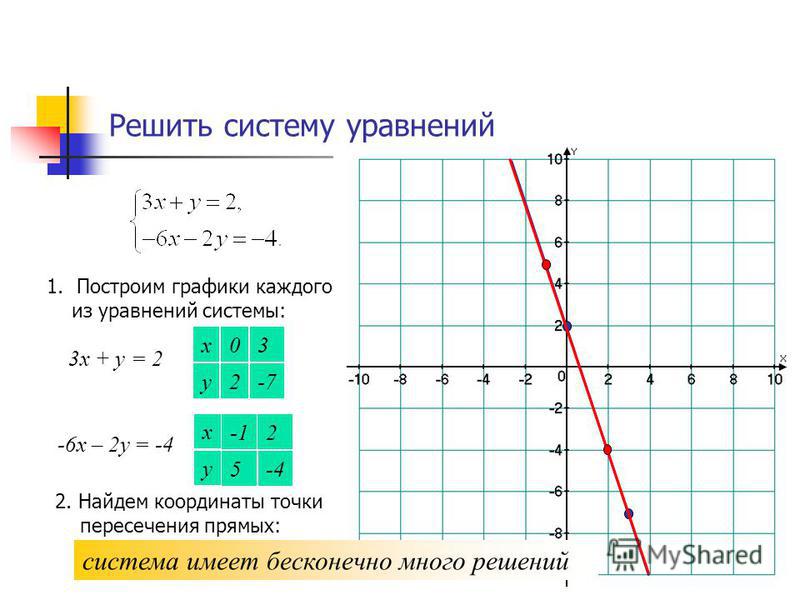
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и диф уравнение онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «график дифференциального уравнения онлайн».Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как график дифференциального уравнения онлайн,диф уравнение онлайн,диф уравнения онлайн,диф уравнения онлайн с подробным решением,дифур онлайн,дифуры онлайн,дифуры онлайн с решением,дифф уравнения онлайн,дифференциальное уравнение калькулятор онлайн,дифференциальное уравнение онлайн,дифференциальное уравнение онлайн калькулятор,дифференциальное уравнение онлайн решение,дифференциальное уравнение онлайн с подробным решением,дифференциальное уравнение первого порядка онлайн,дифференциальное уравнение решение онлайн,дифференциальные однородные уравнения онлайн,дифференциальные уравнения 1 порядка онлайн,дифференциальные уравнения 2 порядка онлайн,дифференциальные уравнения второго порядка онлайн,дифференциальные уравнения калькулятор,дифференциальные уравнения калькулятор онлайн,дифференциальные уравнения калькулятор онлайн с подробным,дифференциальные уравнения калькулятор онлайн с подробным решением,дифференциальные уравнения однородные онлайн,дифференциальные уравнения онлайн,дифференциальные уравнения онлайн второго порядка,дифференциальные уравнения онлайн калькулятор,дифференциальные уравнения онлайн калькулятор с подробным решением,дифференциальные уравнения онлайн однородные,дифференциальные уравнения онлайн первого порядка,дифференциальные уравнения онлайн решение,дифференциальные уравнения онлайн с подробным решением,дифференциальные уравнения онлайн с разделяющимися переменными онлайн,дифференциальные уравнения онлайн с решением,дифференциальные уравнения первого порядка калькулятор онлайн,дифференциальные уравнения первого порядка онлайн,дифференциальные уравнения первого порядка онлайн калькулятор,дифференциальные уравнения решение онлайн,дифференциальные уравнения с разделяющимися переменными калькулятор онлайн,дифференциальные уравнения с разделяющимися переменными онлайн,дифференциальные уравнения с разделяющимися переменными онлайн калькулятор,дифференциальные уравнения с разделяющимися переменными уравнения онлайн,дифференциальные уравнения с решением онлайн,дифференцированные уравнения онлайн,дифференцированные уравнения онлайн решение,диффуры онлайн,ду онлайн,ду онлайн решение,ду решить онлайн,задача коши для дифференциального уравнения онлайн,задача коши онлайн,задача коши онлайн для дифференциального уравнения,задача коши онлайн калькулятор,задача коши онлайн с подробным решением,изоклины онлайн,калькулятор диф уравнений,калькулятор диф уравнений онлайн,калькулятор дифференциалов онлайн,калькулятор дифференциальное уравнение онлайн,калькулятор дифференциальные уравнения,калькулятор дифференциальные уравнения с разделяющимися переменными онлайн,калькулятор дифференциальных уравнений,калькулятор дифференциальных уравнений онлайн,калькулятор дифференциальных уравнений онлайн с подробным решением,калькулятор дифференциальных уравнений с подробным решением,калькулятор дифференциальных уравнений с подробным решением онлайн,калькулятор онлайн дифференциальное уравнение,калькулятор онлайн дифференциальные уравнения,калькулятор онлайн дифференциальные уравнения с разделяющимися переменными,калькулятор онлайн дифференциальных уравнений,калькулятор онлайн задача коши,калькулятор онлайн решения дифференциальных уравнений,калькулятор решения дифференциальных уравнений онлайн,коши калькулятор онлайн,коши онлайн калькулятор,линейные дифференциальные уравнения первого порядка онлайн решение,метод изоклин онлайн калькулятор,найдите общее решение дифференциального уравнения онлайн,найдите частное решение дифференциального уравнения,найти дифференциал второго порядка онлайн,найти общее и частное решение дифференциального уравнения калькулятор,найти общее решение,найти общее решение дифференциального уравнения,найти общее решение дифференциального уравнения второго порядка онлайн,найти общее решение дифференциального уравнения калькулятор онлайн,найти общее решение дифференциального уравнения онлайн,найти общее решение дифференциального уравнения онлайн калькулятор,найти общее решение дифференциального уравнения онлайн с решением,найти общее решение дифференциального уравнения онлайн с решением онлайн,найти общее решение дифференциального уравнения первого порядка онлайн,найти общее решение уравнения,найти общее решение уравнения онлайн,найти общие интегралы дифференциальных уравнений онлайн,найти общий интеграл дифференциального уравнения калькулятор онлайн,найти общий интеграл дифференциального уравнения онлайн,найти общий интеграл дифференциального уравнения онлайн калькулятор,найти общий интеграл дифференциального уравнения онлайн с решением,найти решение дифференциального уравнения онлайн с решением,найти решение задачи коши онлайн,найти решение задачи коши онлайн с подробным решением,найти решение задачи коши онлайн с решением,найти частное решение дифференциального уравнения калькулятор,найти частное решение дифференциального уравнения калькулятор с решением,найти частные решения дифференциальных уравнений онлайн,общее решение дифференциального уравнения онлайн,общее решение найти,общий интеграл дифференциального уравнения онлайн,общий интеграл дифференциального уравнения онлайн калькулятор,однородные дифференциальные уравнения онлайн,однородные дифференциальные уравнения первого порядка онлайн,оду решение,онлайн диф уравнение,онлайн дифференциальное уравнение первого порядка,онлайн дифференциальные уравнения второго порядка,онлайн калькулятор диф уравнений,онлайн калькулятор дифференциальное уравнение,онлайн калькулятор дифференциальные уравнения с разделяющимися переменными,онлайн калькулятор дифференциальных уравнений,онлайн калькулятор дифференциальных уравнений с подробным решением,онлайн калькулятор задача коши,онлайн калькулятор коши,онлайн калькулятор решения дифференциальных уравнений,онлайн найти общее решение дифференциального уравнения первого порядка,онлайн решение диф уравнений,онлайн решение дифференциального уравнения,онлайн решение дифференциальное уравнение,онлайн решение дифференциальные уравнения,онлайн решение дифференциальных уравнений,онлайн решение дифференциальных уравнений 2 порядка,онлайн решение дифференциальных уравнений второго порядка,онлайн решение дифференциальных уравнений коши,онлайн решение дифференциальных уравнений первого порядка,онлайн решение дифференциальных уравнений с подробным решением,онлайн решение дифференциальных уравнений с разделяющимися переменными,онлайн решение дифференциальных уравнений с решением,онлайн решение ду 2 порядка,онлайн решение линейных дифференциальных уравнений,онлайн решение однородных дифференциальных уравнений,онлайн решение однородных уравнений,онлайн решение систем дифференциальных уравнений,онлайн решение системы дифференциальных уравнений,онлайн решение уравнение коши,онлайн решение уравнений коши онлайн,онлайн решение уравнений с разделяющимися переменными,онлайн решения дифференциальных уравнений,онлайн частное решение дифференциального уравнения,определить тип дифференциального уравнения онлайн,проинтегрировать дифференциальное уравнение онлайн,решение диф уравнений онлайн,решение диф уравнений онлайн с полным решением,решение дифуров онлайн,решение дифф уравнений онлайн,решение дифференциального уравнения онлайн,решение дифференциальное уравнение онлайн,решение дифференциальные уравнения онлайн,решение дифференциальных однородных уравнений первого порядка онлайн,решение дифференциальных систем уравнений онлайн,решение дифференциальных уравнений 2 порядка онлайн,решение дифференциальных уравнений второго порядка онлайн,решение дифференциальных уравнений второго порядка онлайн с решением,решение дифференциальных уравнений коши онлайн,решение дифференциальных уравнений онлайн,решение дифференциальных уравнений онлайн коши,решение дифференциальных уравнений онлайн с подробным решением,решение дифференциальных уравнений онлайн с разделяющимися переменными,решение дифференциальных уравнений онлайн с решением,решение дифференциальных уравнений онлайн с решением в полном виде,решение дифференциальных уравнений первого порядка онлайн,решение дифференциальных уравнений первого порядка онлайн с решением,решение дифференциальных уравнений с подробным решением онлайн,решение дифференциальных уравнений с разделяющимися переменными калькулятор,решение дифференциальных уравнений с разделяющимися переменными онлайн,решение дифференциальных уравнений с решением онлайн,решение ду 2 порядка онлайн,решение ду онлайн,решение ду онлайн с полным решением,решение задачи коши онлайн с подробным решением,решение линейных дифференциальных уравнений онлайн,решение однородных дифференциальных уравнений онлайн,решение однородных уравнений онлайн,решение онлайн дифференциального уравнения,решение онлайн дифференциальное уравнение,решение онлайн дифференциальных уравнений первого порядка,решение онлайн дифференциальных уравнений с разделяющимися переменными,решение онлайн линейных дифференциальных уравнений,решение онлайн уравнений с разделяющимися переменными,решение систем дифференциальных уравнений онлайн,решение системы дифференциальных уравнений онлайн,решение уравнение коши онлайн,решение уравнений с разделяющимися переменными онлайн,решения дифференциальных уравнений онлайн,решить диф уравнение онлайн,решить дифференциальное линейное уравнение онлайн,решить дифференциальное уравнение второго порядка онлайн с решением,решить дифференциальное уравнение онлайн,решить дифференциальное уравнение онлайн с подробным решением,решить дифференциальное уравнение онлайн с решением,решить дифференциальное уравнение первого порядка онлайн,решить дифференциальное уравнение первого порядка онлайн с решением,решить дифференциальное уравнение с разделяющимися переменными онлайн,решить дифференциальное уравнение с решением онлайн,решить ду,решить ду онлайн,решить задачу коши онлайн,решить задачу коши онлайн калькулятор с подробным решением,решить задачу коши онлайн с решением,решить линейное дифференциальное уравнение онлайн,решить однородное дифференциальное уравнение онлайн,решить онлайн дифференциальное уравнение,решить онлайн ду,решить онлайн задачу коши,решить онлайн линейное дифференциальное уравнение,решить онлайн уравнение в полных дифференциалах,решить систему дифференциальных уравнений онлайн,решить уравнение y x y,решить уравнение в полных дифференциалах онлайн,система дифференциальных уравнений онлайн,система дифференциальных уравнений онлайн калькулятор с решением,уравнение в полных дифференциалах решить онлайн,уравнение коши онлайн,уравнение коши решение онлайн,уравнения с разделяющимися переменными онлайн,уравнения с разделяющимися переменными онлайн калькулятор,частное решение дифференциального уравнения калькулятор,частное решение дифференциального уравнения онлайн.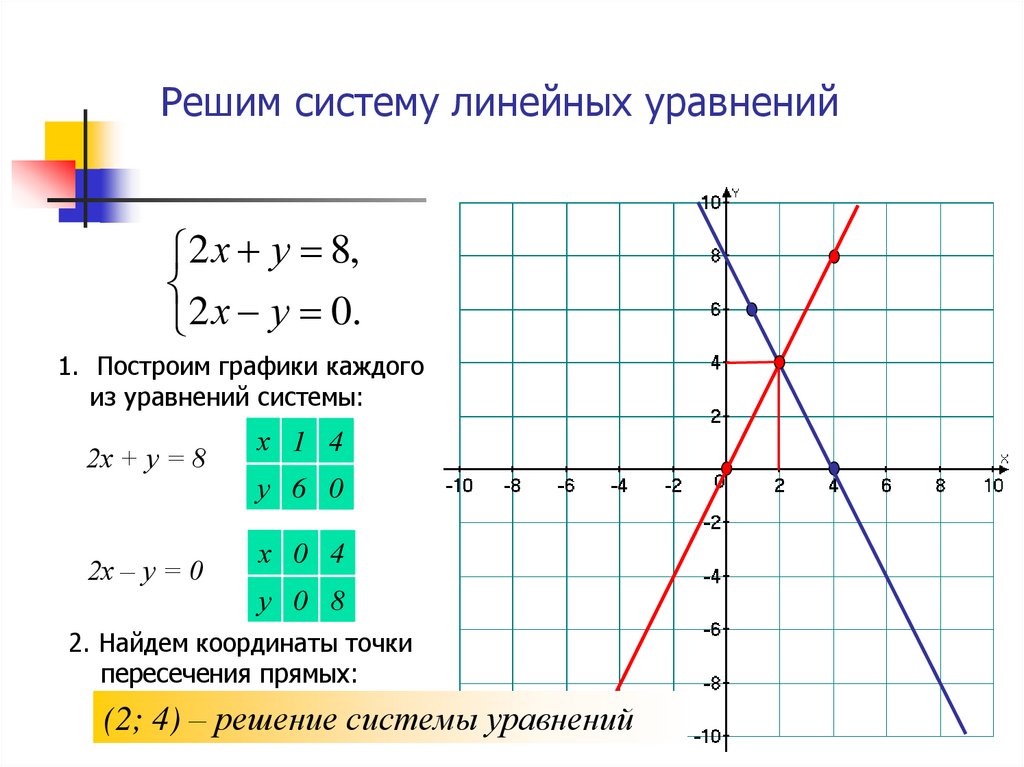
Где можно решить любую задачу по математике, а так же график дифференциального уравнения онлайн Онлайн?
Решить задачу график дифференциального уравнения онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор метода построения системы уравнений
Решатели Алгебра Калькуляторы
Инструкции: Используйте этот калькулятор для решения системы двух линейных уравнений графическим методом.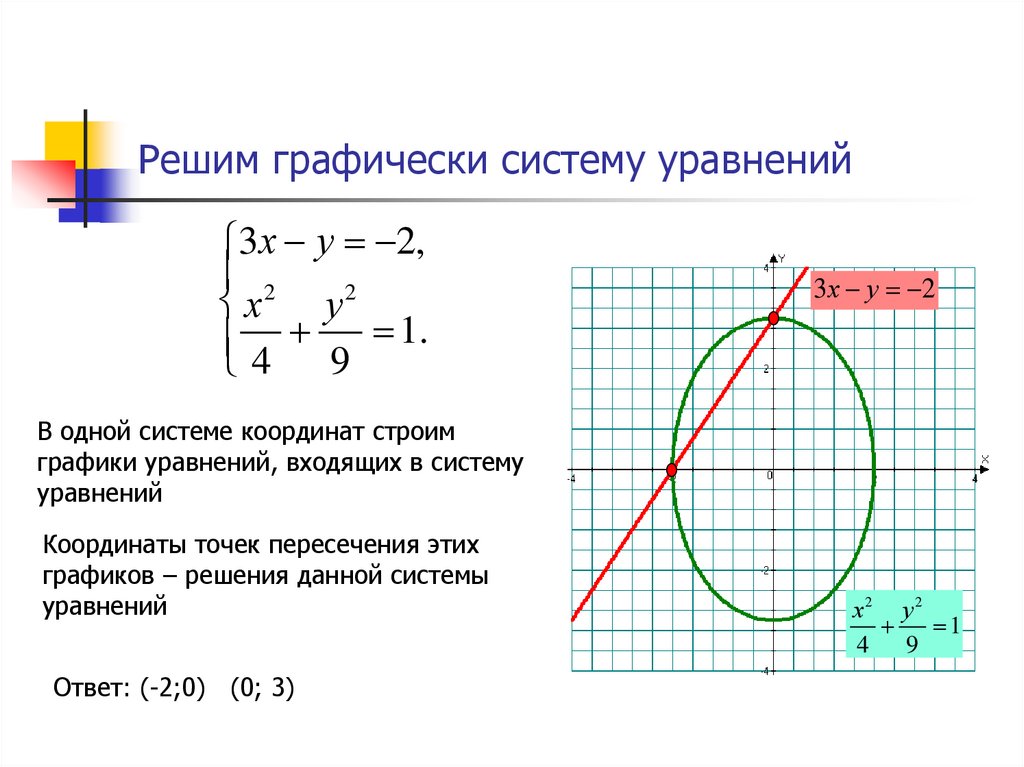
Введите два допустимых линейных уравнения в соответствующие поля.
ниже:
Введите линейное уравнение (Пример: y = 2x + 3, 3x — 2y = 3 + 2/3 x и т. д.)
Введите другое линейное уравнение (Пример: y = 2x + 3, 3x — 2y = 3 + 2 /3 x и т. д.)
(дополнительно) Минимум x =
(необязательно) Максимум x =
Системы линейных уравнений очень часто встречаются в различном контексте алгебры. Наиболее часто встречающиеся системы в базовых курсах алгебры представляют собой системы 2 на 2, которые состоят из двух прямых уравнений и двух переменных.
Такие системы «два на два» часто появляются при решении задач со словами, задач на пропорции и задач на присваивание с ограничением.
Естественно, крупнее
системы (с большим количеством переменных и уравнений) также распространены, здесь сосредоточьтесь только на системах 2×2, потому что их мы можем изобразить графически.
Как пользоваться графическим методом
Графический метод состоит в представлении каждого из линейных уравнений в виде линии на графике. Затем нам нужно найти пересечение точки между двумя линиями, используя наблюдение, что точка пересечения линии (если она существует) будет решением системы.
Что произойдет, если перекрестка не существует? Это было бы в том случае, если бы линии были параллельны, но не были бы одной и той же линией, и в этом случае нет пересечение. Правило понятно: когда между линиями нет пересечения, у системы нет решения.
Возможен и третий случай: линии могут быть параллельны, но на самом деле идентичны (то есть это одна и та же линия).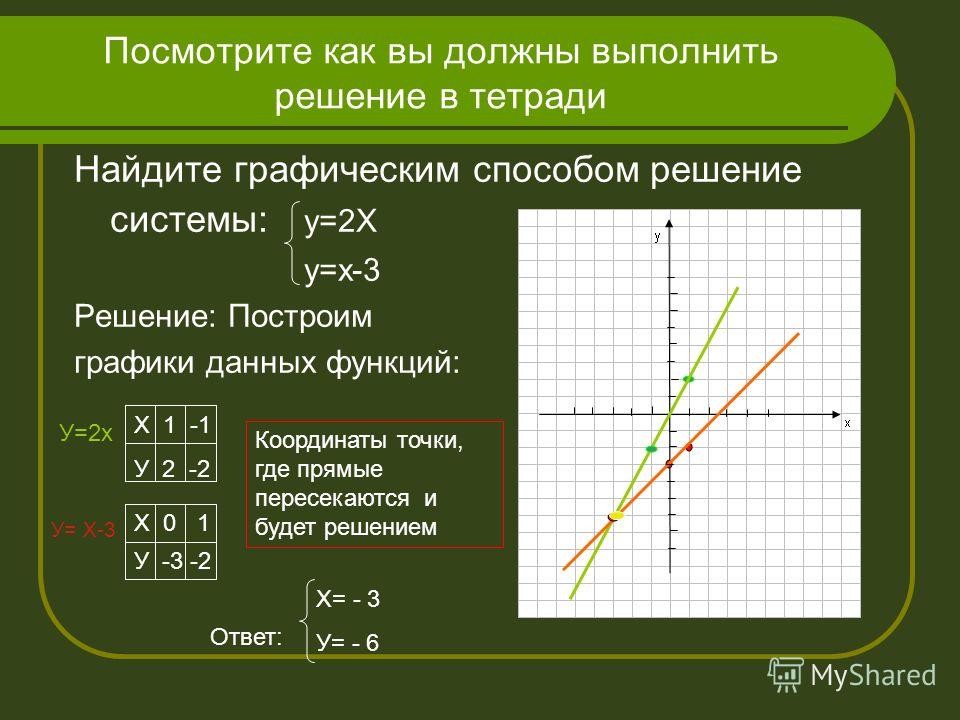
Итак, сколько перекрестков
баллы у тебя есть? Да, вы правы: у вас бесконечные точки пересечения, а значит, у вас есть бесконечные решения.
Решение систем уравнений путем графического отображения ответов
Итак, методология проста: вы начинаете с линейной системы, и первое, что вы делаете, это графически изображаете два линейные уравнения.
Затем вы смотрите на график и оцениваете, пересекаются ли линии только в одной точке (что происходит, если линии имеют разные наклоны, и в этом случае у вас есть уникальное решение.
Если нет, посмотрите, параллельны ли они и различны, и в этом случае решений нет. В противном случае, если два прямые равны, то у нас есть бесконечные решения.
Как решить систему уравнений на графическом калькуляторе?
Все системы работают по-разному. В этом случае с этим графическим калькулятором все, что вам нужно сделать, это ввести два линейных уравнения, даже если они
не совсем упрощенный.
Калькулятор сначала попытается перевести линии в точку пересечения наклона и предоставит вам график и
приближенная оценка решения.
Различные калькуляторы дают разные результаты, но большое преимущество этого калькулятора в том, что он обеспечивает все этапы процесса.
Как составить систему уравнений из графика?
Линейные функции однозначно связаны. То есть одно линейное уравнение связано только с одной и одной прямой, и наоборот, линия связаны только с одним линейным уравнением и одним линейным уравнением.
Итак, чтобы написать системы уравнений с графика, нужно работать с каждой строкой отдельно. Возьмите одну линию и определите две точки на линия. С этими двумя точками вы можете вычислить наклон линии.
Затем, с учетом наклона линии и точки пересечения с осью Y,
вы можете написать уравнение линии в форме пересечения наклона.
Метод построения системы уравнений калькулятор системы линейных уравнений калькулятор решения уравнения системы s
Systems of Equations Solver: Wolfram|Alpha
WolframAlpha
Решение уравнений и систем уравнений с помощью Wolfram|Alpha
Мощный инструмент для поиска решений систем уравнений и ограничений
Wolfram|Alpha способен решать самые разнообразные систем уравнений. Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, и может специально искать целочисленные решения или решения в другой области. Кроме того, он может решать системы, включающие неравенства и более общие ограничения. 92 = 4, y = x
- Посмотреть другие примеры »
Доступ к инструментам мгновенного обучения
Немедленная обратная связь и руководство с пошаговыми решениями и генератором проблем Wolfram
Узнайте больше о:
- Шаг пошаговые решения »
- Генератор задач Wolfram »
Что такое системы уравнений?
Система уравнений представляет собой набор из одного или нескольких уравнений, включающих ряд переменных.
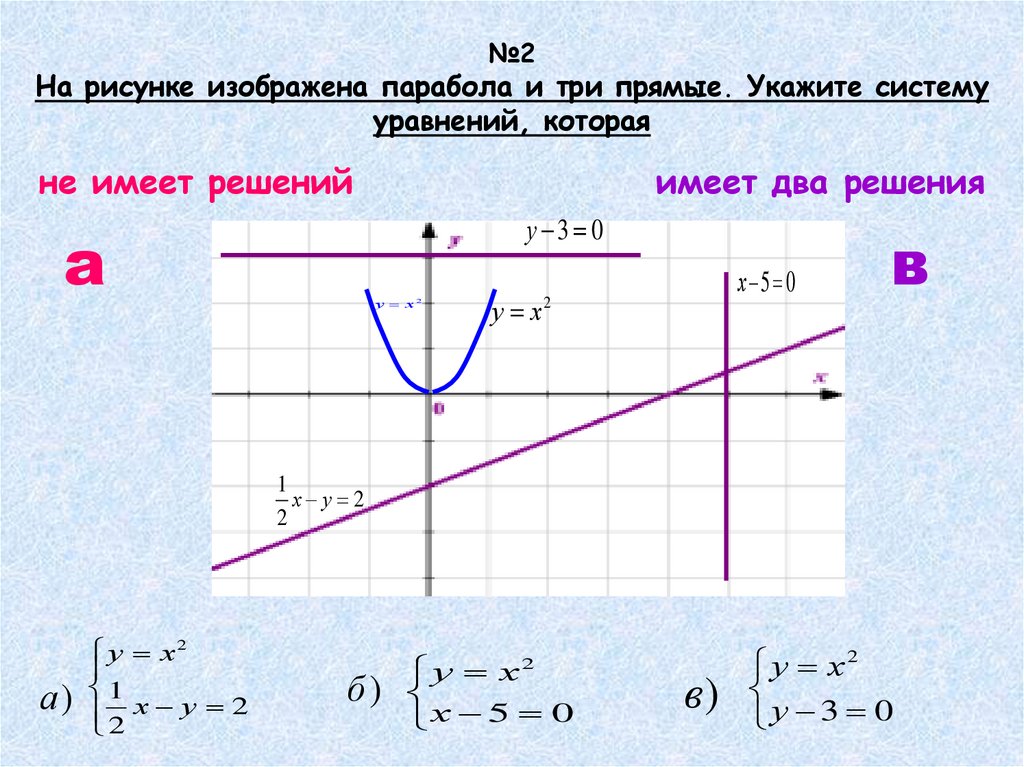
Решениями систем уравнений являются такие отображения переменных, что удовлетворяются все уравнения компонентов, другими словами, места, в которых все эти уравнения пересекаются. Решить систему значит найти все такие общие решения или точки пересечения.
Системы линейных уравнений — распространенное и применимое подмножество систем уравнений. В случае двух переменных эти системы можно рассматривать как линии, проведенные в двумерном пространстве. Если все прямые сходятся в одной точке, то говорят, что система непротиворечива и имеет решение в этой точке пересечения. В противном случае система называется несовместной, не имеющей решений. Системы линейных уравнений, включающие более двух переменных, работают аналогично, имея либо одно решение, либо отсутствие решений, либо бесконечное количество решений (последнее в случае, если все уравнения для компонентов эквивалентны).
Возможны и более общие системы, включающие нелинейные функции. Они обладают более сложными наборами решений, включающими одно, нулевое, бесконечное или любое количество решений, но работают аналогично линейным системам в том смысле, что их решениями являются точки, удовлетворяющие всем задействованным уравнениям.
Ваш комментарий будет первым