График прямой в пространстве онлайн: Построить трехмерный график онлайн

Содержание

Нахождение уравнений прямой, заданной пересечением двух плоскостей

УчебаМатематикаГеометрия

Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве. Калькулятор выводит канонические и параметрические уравнения прямой, а также координаты точки, принадлежащей прямой и направляющего вектора прямой.

Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:

Записать канонические (или параметрические) уравнения прямой, заданной уравнениями двух плоскостей
.

Вы задаете коэффициенты уравнений плоскостей, А₁, B₁, C₁, D₁ и A₂, B₂, C₂, D₂, калькулятор выдает уравнения прямой в параметрической и канонической формах, а также найденную точку, принадлежащую прямой и направляющий вектор прямой.

Обратите внимание, в том случае если уравнения плоскостей заданы в виде

при вводе коэффициентов D₁ и D₂ надо поменять знак.

Немного теории, как обычно, можно почерпнуть под калькулятором

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Общее уравнение первой плоскости

Общее уравнение второй плоскости

Точка, принадлежащая прямой

Направляющий вектор прямой

Канонические уравнения прямой

Параметрические уравнения прямой

Точность вычисления

Знаков после запятой: 2

Канонические уравнения прямой, заданной пересечением двух плоскостей

Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.

Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.

Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .

Точка и вектор дают нам канонические уравнения прямой:

Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.

В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:

В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:

Эти случаи также учитываются калькулятором.

Параметрические уравнения прямой, заданной пересечением двух плоскостей

Зная точку, принадлежащую прямой и ее направляющий вектор, несложно записать и параметрические уравнения прямой.
Для точки , принадлежащей прямой, и направляющего вектора параметрические уравнения прямой выглядят так:

Ссылка скопирована в буфер обмена

Уравнения прямой в пространстве

Канонические уравнения прямой в пространстве
Уравнения прямой, проходящей через две данные точки
Прямая как линия пересечения плоскостей
Параметрические уравнения прямой в пространстве

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.

Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m, n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа

m, n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz, т. е. плоскости yOz.

Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz.

Решение. Найдём точку пересечения данной плоскости с осью Oz. Так как любая точка, лежащая на оси

Oz, имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0, получим 4z — 8 = 0 или z = 2. Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2). Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :

или

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.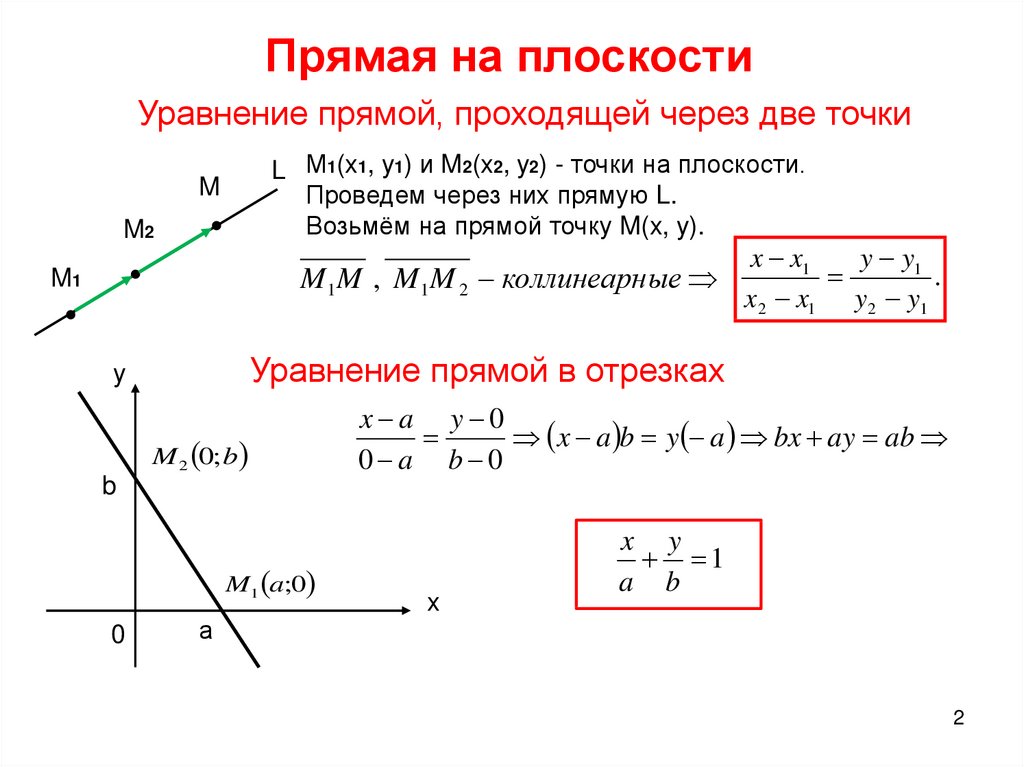

Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .

Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:

или

Так как , то искомая прямая перпендикулярна оси Oy.

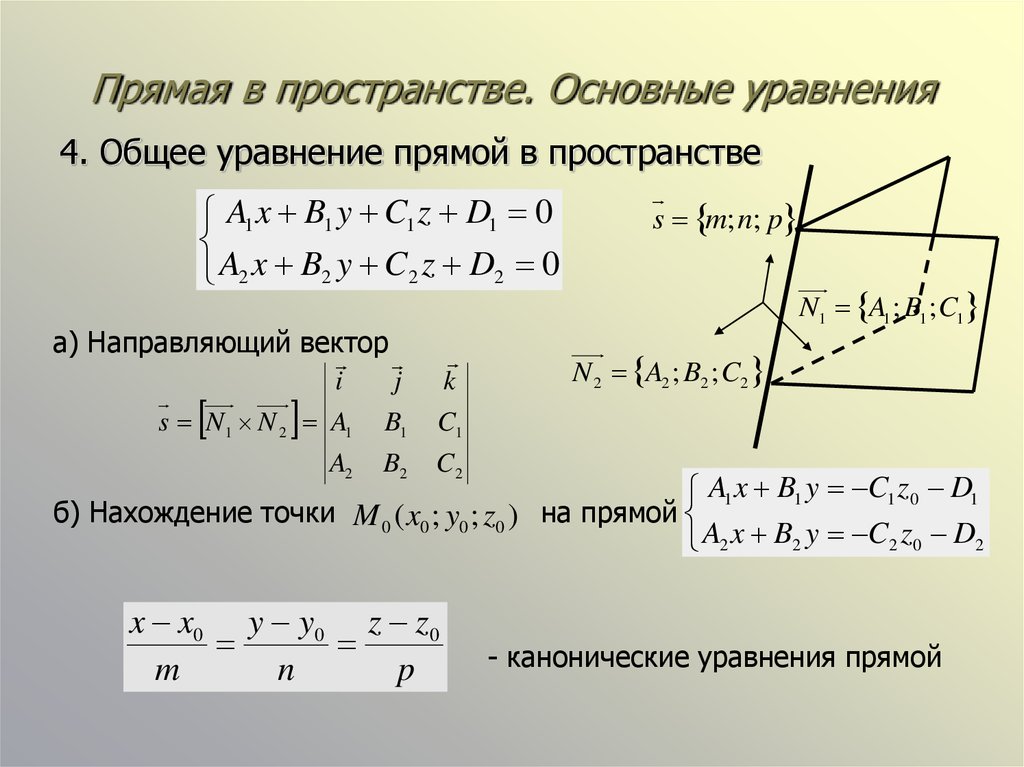
Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений

Уравнения системы называются также общими уравнениями прямой в пространстве.

Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями

Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой.

Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz.

Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0. Поэтому, полагая в данной системе уравнений x = 0, получим систему с двумя переменными:

Её решение y = 2, z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0, получим систему

Её решение x = -2, z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью

xOz.

Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0):

или после деления знаменателей на -2:

где .

Если даны некоторая точка и направляющий вектор, то можно составить не только канонические, но и параметрические уравнения прямой в пространстве. Пусть даны и направляющий вектор .

Тогда

где t — параметр .

Пример 4. Даны точка и направляющий вектор . Составить параметрические уравнения прямой.

Решение:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

Пройти тест по теме Прямая и плоскость

Всё по теме «Прямая и плоскость»

Плоскость

Уравнения плоскости, взаимное расположение плоскостей

Прямая в пространстве

Уравнения прямой в пространстве

Задачи на плоскость и прямую в пространстве

Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке

Прямая на плоскости

Уравнение прямой с угловым коэффициентом
Общее уравнение прямой на плоскости
Уравнение прямой в отрезках
Каноническое уравнение прямой на плоскости
Параметрические уравнения прямой на плоскости
Нормальное уравнение прямой на плоскости, расстояние от точки до прямой
Угол между двумя прямыми

Простая в использовании программа для создания линейных диаграмм

Решатели Статистика

Инструкции : Используйте этот конструктор линейных графиков, чтобы создать линейный график, используя форму ниже. Все, что вам нужно сделать, это ввести данные Y (и, возможно, ваши метки X). Кроме того, вы можете добавить название к осям.

Данные Y (разделенные запятой или пробелом)

Данные X (разделенные запятой или пробелом)

Введите заголовок (необязательно)

Имя переменной X (необязательно)

Имя переменной Y (необязательно)

Подробнее о линейных диаграммах : Линейная диаграмма или линейный график — это тип графического представления с характеристикой, состоящей в том, что точки данных соединяются прямыми линиями. Этот тип настройки имеет смысл в определенных обстоятельствах, как, например, в случае временного ряда, но в случаях порядка, точечная диаграмма может быть более подходящим (в случае большинства перекрестных данных).

Как создать линейный график?

Линейная диаграмма строится путем соединения набора пар \((x_i,y_i)\) прямыми линиями, начиная с точек слева и вправо.

Графически линейный график выглядит следующим образом:

Другие производители графиков

Мы предоставляем другие создатели графиков, такие как наш график нормальной вероятности , наш Создатель диаграммы Парето , создатель сюжета временных рядов или круговая диаграмма .

Одним из специфических типов калькуляторов линейных графиков является средство для создания оживальных графиков, которое представляет собой линейный график, изображающий кумулятивная таблица частот.

Базовый пакет статистики Графический инструмент Линейный график Создатель линейных диаграмм Плоттер линейных диаграмм Генератор линейных графиков Решатель статистики

Линейная диаграмма—ArcGIS Online Help | Документация

Линейные графики позволяют визуализировать изменения в непрерывном диапазоне, например, во времени или расстоянии. Визуализация изменений с помощью линейной диаграммы позволяет одновременно отображать общую тенденцию и одновременно сравнивать несколько тенденций.

Пример

Создайте линейную диаграмму для визуализации тенденций в криминальных инцидентах в 2014 и 2015 гг.0049

Числовые поля — нет

Разделить по — тип преступления

Интервал — шесть дней

Данные

Конфигурации вкладки «Данные» включают переменные, которые используются для создания линейной диаграммы.

Переменные

Для линейных диаграмм требуется непрерывная переменная даты или числа по оси X и связанное числовое значение на оси Y.

По оси X линейного графика отображается непрерывная переменная, такая как время или расстояние, и рисуется линия, отображающая изменение значения между каждым последовательным интервалом времени или расстояния. Каждый интервал отмечен точкой, соответствующей числовому значению, измеренному по оси Y.

Если для оси X выбрано числовое поле, и каждое число появляется в таблице только один раз, нет необходима агрегация, но должна быть указана переменная числовых полей.

Если для оси X выбрано поле даты, даты объединяются или агрегируются во временные интервалы. Когда линейная диаграмма рисуется с использованием поля даты или агрегированного числового поля, необходимо выбрать метод агрегирования, чтобы указать, как данные будут суммироваться.

Если числовые поля не указаны, на диаграмме будет использоваться метод агрегирования Count, который суммирует количество записей, появляющихся в каждый интервал времени или расстояния. Например, в наборе данных о криминальных происшествиях поле даты разбито на двухнедельные интервалы с помощью метода агрегирования Count. В полученной диаграмме для каждого двухнедельного интервала будет отображаться маркер, показывающий, сколько преступлений было совершено за эти две недели.

Если указаны значения числовых полей, метод агрегации может быть одним из следующих:

Сумма
Среднее
Медиана
Без агрегации тот же график для сравнения тенденций.
Линейные диаграммы с несколькими сериями можно создать, добавив несколько числовых полей или установив поле «Разделить по категориям».
При добавлении нескольких значений числовых полей рисуется одна линия для визуализации изменения для каждого числового поля. Например, в наборе данных о криминальных происшествиях поле даты разбито на двухнедельные интервалы с помощью метода агрегирования Sum и двух значений числовых полей, PropertyLoss и TotalDamage. Полученная диаграмма будет отображать две линии, одна из которых представляет сумму PropertyLoss, а другая — сумму TotalDamage для каждого двухнедельного интервала.
Поле категории также можно использовать для разделения линейной диаграммы на несколько рядов. Например, в наборе данных о криминальных происшествиях поле даты разбито на двухнедельные интервалы с помощью метода агрегирования Count и поля CrimeType Split by. В итоговой диаграмме будут отображаться линии, представляющие общее количество преступлений каждого типа (например, краж, вандализма и поджогов), которые имели место за эти две недели.
Разделение по категориям невозможно применить, если добавлено более одного числового значения поля.
Поля категории с большим количеством уникальных значений не подходят для разделения поля на несколько серий.
Биннинг по времени
Агрегирование по времени, или биннинг, происходит автоматически, когда для оси X выбрано поле даты. Несколько параметров управляют размером интервала и соответствующими настройками, применяемыми к биннингу.
Интервал
Временные данные объединяются во временные интервалы по оси x. Интервал по умолчанию выбирается на основе временного экстента набора данных и может быть изменен вручную с помощью параметра «Интервал».
Выравнивание интервала
Временные интервалы могут быть выровнены по первой точке данных или по последней точке данных.
Привязка к первой точке данных инициирует бинирование с самой ранней датой и работает вперед.
Привязка к последней точке данных инициирует бинирование с самой последней датой и работает в обратном порядке.
Выравнивание интервалов важно учитывать, поскольку последний созданный бин может быть частично пустым, что может создать ложное впечатление, что в течение этого времени наблюдается провал в значении или подсчете, когда на самом деле сбор данных начался или закончился в течение промежутка времени это мусорное ведро. Чтобы избежать смещения бина, установите флажок Обрезать неполный интервал. Это удаляет частично заполненную корзину из визуализации:
Пустые ячейки
В зависимости от разреженности набора данных и размер временного интервала, выбранный для бинирования, могут быть бины, которые не содержат данных. Пустые бины могут рассматриваться как нулевые при отсутствии данные действительно представляют собой нулевое значение (например, отсутствие болезней были зарегистрированы в мае или дождей не было в течение недели). Недопустимо присваивать нулевое значение бину, в котором нет данных. существует, потому что ничего не было собрано (например, нет чтения из датчик температуры не означает, что была температура нуль).
Доступны три варианта с пустыми ячейками:
- Обрабатывать их как ноль (Обрабатывать как ноль) — это наиболее подходит при подсчете инцидентов, так как инциденты не учитываются. вероятно, означает, что инцидентов не было.
- Интерполировать соседние значения (линия соединения) — нулевые значения можно визуально интерполировать с помощью соединение линии между бункерами по обе стороны от пустого мусорное ведро
- Break the line (Перерыв линии) — оставляйте пустое место там, где падает пустая корзина.
Метки
Вы можете включить метки, отображающие значение каждой строки или ряда, включив параметр Показать метки данных.
Series
Конфигурации вкладки Series используются для изменения цвета, ширины, стиля и метки линии на линейной диаграмме.
Оси
Конфигурации вкладки Оси используются для изменения спецификаций осей X и Y.
Вы можете отформатировать способ отображения числовых значений по осям X и Y, указав количество знаков после запятой и включив ли разделитель тысяч. Ось X можно отформатировать только в том случае, если она отображает числовое поле, а не поле даты.
Минимальные и максимальные границы по оси Y по умолчанию устанавливаются на основе диапазона значений данных, представленных на оси Y. Вы можете настроить эти значения, введя новые значения «Минимальные границы» и «Максимальные границы». Нажмите «Сброс», чтобы вернуть ось, привязанную к значению по умолчанию.
Логарифмическая шкала
По умолчанию оси линейной диаграммы отображаются в линейной шкале. Числовые оси (без дат) можно отображать в логарифмическом масштабе с помощью ползунка Логарифмический масштаб.
Логарифмические шкалы полезны при визуализации данных с большой положительной асимметрией, когда большинство точек данных имеют небольшое значение, а несколько точек данных имеют очень большие значения. Изменение масштаба оси не меняет значения данных — только то, как они отображаются.
Линейные шкалы основаны на сложении, а логарифмические шкалы основаны на умножении.
На линейной шкале каждое приращение по оси представляет такое же расстояние по стоимости. Например, на осевой диаграмме ниже каждое приращение на оси увеличивается на 10.
В логарифмическом масштабе приращение увеличивается на величину. В на осевой диаграмме ниже каждое приращение по оси увеличивается на умножение на 10.
Логарифмические шкалы не могут отображать отрицательные значения или ноль. Если вы используете логарифмическую шкалу для переменной, содержащей отрицательные значения или нули, эти значения не будут отображаться на диаграмме.
Направляющие
Конфигурации вкладки Направляющие используются для добавления направляющих или диапазонов направляющих на диаграмму.
Направляющие линии или диапазоны могут быть добавлены к диаграммам в качестве ссылки или способа выделения важных значений. Направляющие добавляются нажатием кнопки «Добавить направляющую», а затем выбором «Добавить направляющую оси X» или «Добавить направляющую оси Y».
Направляющие оси X не поддерживаются для линейных диаграмм, использующих дату в качестве переменной оси X.
Чтобы создать направляющую линию, введите начальное значение в том месте, где должна быть проведена линия. Чтобы создать направляющий диапазон, введите начальное значение и конечное значение. Вы также можете изменить внешний вид направляющей линии или диапазона. Для линий можно обновить стиль, ширину и цвет. Для диапазонов можно обновить цвет заливки.
При желании вы можете изменить имя направляющей с помощью параметра Имя направляющей и добавить текст к направляющей с помощью параметра Метка направляющей (например, Медиана).
Вы можете выбрать, будет ли направляющая отображаться поверх диаграммы или под диаграммой, используя кнопки «Выше» и «Ниже» в параметре «Визуализация».
Формат
Конфигурации вкладки Формат используются для изменения внешнего вида диаграммы путем форматирования элементов текста и символов.
Варианты форматирования диаграммы включают следующее:
Параметры форматирования диаграммы включают следующие:
Общие
Конфигурации вкладки Общие используются для обновления заголовков диаграммы, осей и условных обозначений.