|
y(x) = цвет линия убрать Добавить график функции: обычный: y(x)заданный параметрически: x(t) и y(t) в полярной системе координат по точкам (по значениям) Ось Х
|
Занятие 2.
 Построение графика распределения. Построение гистограммы — Основы доказательной медицины. Биомедицинская статистика. — Внауке.by
Построение графика распределения. Построение гистограммы — Основы доказательной медицины. Биомедицинская статистика. — Внауке.by
ПОСТРОЕНИЕ ГРАФИКА РАСПРЕДЕЛЕНИЯ
В программе STATISTICA реализован графически-ориентированный подход к анализу данных. Он заключается в том, чтобы получать всестороннее визуальное представление данных на всех этапах статистической обработки. В связи с этим программа обладает огромным набором различных типов графиков, которые можно построить, обратившись к пункту главного меню Graphs (рисунок ниже) или к соответствующим закладкам того или иного статистического модуля.
Выбор типа графика в программе STATISTICA.
Для того чтобы программа смогла построить график распределения, из данных столбца «Лейкоциты» нужно сформировать вариационный ряд, т.е. в двойной ряд чисел, в котором содержатся значения анализируемого признака и частоты их встречаемости в выборке. Перед тем как сделать это, добавим два столбца в таблицу Spreadsheet, содержащую данные о числе лейкоцитов. Подведите курсор к заголовку столбца «Лейкоциты» и нажмите правую клавишу мыши. В выскочившем контекстном меню выберите пункт Add Variables (добавить переменные). Появится диалоговое окно, в котором нужно указать, сколько переменных мы намерены добавить (поле How Many: выставляем 2) и после какой из существующих переменных их нужно вставить (поле After: наберите слово «Лейкоциты»). Остальные настройки установите так, как это показано на рисунке Диалоговое окно «Add Variables». В таблице появятся два новых столбца с названиями «NewVar1» и «NewVar2». Переименуйте их в «Количество лейкоцитов» и «Количество пациентов» соответственно (о том, как задать имя переменной, рассказано выше).
Диалоговое окно «Add Variables»
Теперь построим вариационный ряд. Для этого в пункте основного меню Statistics (Статистические процедуры) выберем модуль Basic Statistics/Tables (Основные статистические показатели/Таблицы), а в нем — опцию Frequency Tables (Таблицы частот).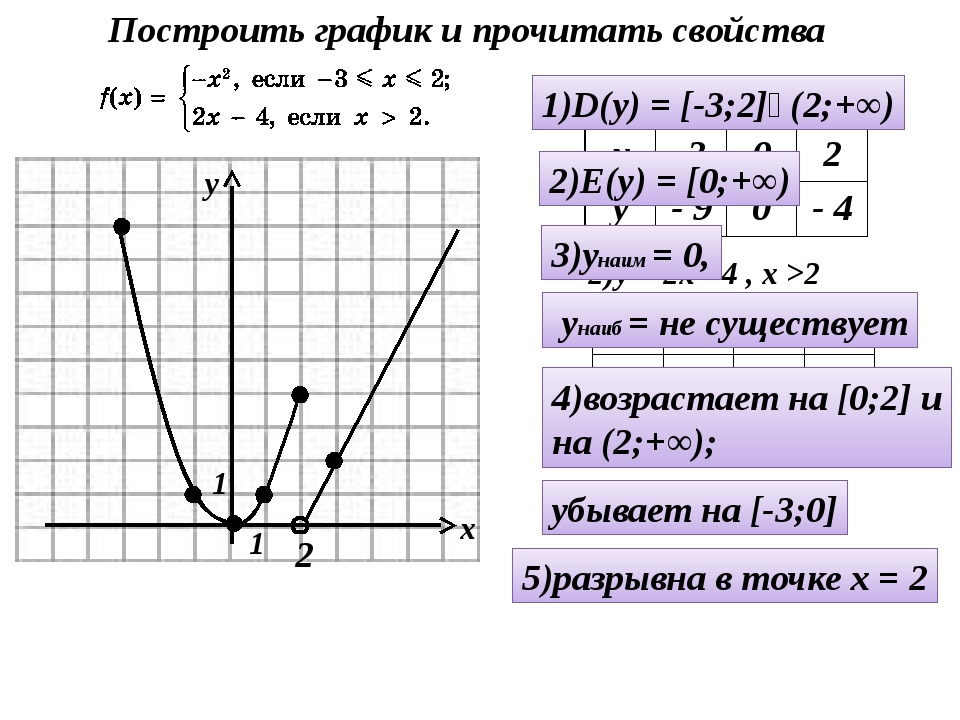 В появившемся диалоговом окне программе необходимо указать, какую именно переменную мы собираемся анализировать. Для этого служит кнопка Variables (переменные) (рисунок ниже). При нажатии на нее всплывает еще одно окошко (Select the variables for the analysis), основная часть которого занята списком переменных, имеющихся в таблице Spreadsheet. Дважды кликните по пункту «Лейкоциты», а затем нажмите либо кнопку Summary: Frequency Tables (Результат: Частотные таблицы), либо Summary (Результат), либо просто клавишу «Ввод» на клавиатуре.
В появившемся диалоговом окне программе необходимо указать, какую именно переменную мы собираемся анализировать. Для этого служит кнопка Variables (переменные) (рисунок ниже). При нажатии на нее всплывает еще одно окошко (Select the variables for the analysis), основная часть которого занята списком переменных, имеющихся в таблице Spreadsheet. Дважды кликните по пункту «Лейкоциты», а затем нажмите либо кнопку Summary: Frequency Tables (Результат: Частотные таблицы), либо Summary (Результат), либо просто клавишу «Ввод» на клавиатуре.
Выбор переменной для анализа Frequency Tables
В итоге программа выдаст таблицу, представляющую собой «расширенный» вариант вариационного ряда. В этой таблице имеются следующие столбцы:
- Category (Категория): содержит ранжированные численные значения анализируемой переменной, отмеченные в выборке. В случае с нашим примером видим, что количество лейкоцитов у пациентов изменялось от 6,4 до 27.
- Count (Счет): здесь приведены частоты, с которыми в выборке встречались те или иные значения переменной (так, в ходе исследования обнаружено, что уровень лейкоцитов 6,4 был у 1 пациента, 21,4 у 4 пациентов, а 11,6 у 3 пациентов и т.д.).
- Cumulative count: накопленные частоты численных значений переменной.
- Percent: процентная доля, которую составляет каждая из частот от общего числа наблюдений.
- Cumulative percent: накопленные процентные доли частот.
Последняя строка итоговой таблицы называется Missing (Отсутствующие) — она имеет отношение к пропущенным (т.е. не внесенным в таблицу) значениям анализируемой переменной. Таковых в нашем примере нет, в связи с чем, на пересечении столбца Count и строки Missing видим 0.
Рассмотрите внимательно: итоговая таблица анализа Frequency Tables является частью окна с заголовком Workbook (рабочая книга). Такая форма вывода результатов очень удобна и является характерной особенностью программы STATISTICA. Результаты любого анализа, который в дальнейшем применялся бы к данным открытого в текущий момент файла, заносился бы в эту же рабочую книгу на отдельный лист. Структура рабочей книги (= каталог выполненных анализов) отображается в специальном окошке слева. Рабочую книгу можно сохранить в виде самостоятельного файла (с расширением .stw) и при необходимости вернуться к ней в любое время.
Результаты любого анализа, который в дальнейшем применялся бы к данным открытого в текущий момент файла, заносился бы в эту же рабочую книгу на отдельный лист. Структура рабочей книги (= каталог выполненных анализов) отображается в специальном окошке слева. Рабочую книгу можно сохранить в виде самостоятельного файла (с расширением .stw) и при необходимости вернуться к ней в любое время.
Рабочая книга, содержащая результат анализа Frequency Tables.
Для построения графика распределения нам потребуются числа из столбцов Category и Count, которые необходимо будет перенести из итоговой таблицы анализа Frequency Tables в таблицу Spreadsheet. Чтобы скопировать данные из столбца Category, выполните следующие действия:
- Подведите курсор к первой ячейке столбца Category, нажмите левую кнопку мыши и, удерживая ее, доведите курсор до предпоследней ячейки этого же столбца. При этом выделятся все ячейки таблицы (за исключением строки Missing). Все они нам не нужны, поэтому…
- Нажмите правую кнопку мыши и из появившегося контекстного меню выберите пункт Select case names only (Выбрать только имена наблюдений), находящийся в самом верху списка.
- Примените сочетание клавиш Ctrl+C.
- Установите курсор в первую ячейку столбца «Количество лейкоцитов» таблицы Spreadsheet.
- Примените сочетание клавиш Ctrl+V. Готово!
!! Данные из столбца Count итоговой таблицы анализа Frequency tables легко выделяются, копируются (Ctrl+C) и вставляются в столбец «Количество пациентов» обычным способом (Ctrl+V), в чем вы можете убедиться сами… В результате описанных операций по переносу данных таблица Spreadsheet должна принять вид, подобный приведенному на рисунке.
Результат копирования и переноса данных из столбцов Category и Count итоговой таблицы Frequency Tables в таблицу Spreadsheet
Теперь у нас есть все необходимое, чтобы построить полигон распределения по данным о количестве лейкоцитов у пациентов с перитонитом. В пункте главного меню Graphs (Графики) выберите подпункт 2D Graphs (двухмерные графики), а в нем — опцию Line Plots (Variables) (линейные графики (по переменным)). В появившемся диалоговом окне выберите закладку Advanced (расширенные настройки). На ней в поле Graph Type (Тип графика) выделите XY Trace, а в выпадающем меню Display points (отображать точки) выберите On (Включить). Наконец откройте закладку Options 1, разыщите на ней выпадающее меню Case labels (Подписи наблюдений) и выберите пункт Off (Отключить).
В пункте главного меню Graphs (Графики) выберите подпункт 2D Graphs (двухмерные графики), а в нем — опцию Line Plots (Variables) (линейные графики (по переменным)). В появившемся диалоговом окне выберите закладку Advanced (расширенные настройки). На ней в поле Graph Type (Тип графика) выделите XY Trace, а в выпадающем меню Display points (отображать точки) выберите On (Включить). Наконец откройте закладку Options 1, разыщите на ней выпадающее меню Case labels (Подписи наблюдений) и выберите пункт Off (Отключить).
Окно 2D Line Plots на закладке Advanced
Теперь программе необходимо указать, в каком из столбцов таблицы Spreadsheet находятся данные о количестве лейкоцитов (ось X), а в каком — данные о частотах встречаемости (ось Y). Для этого снова возвращаемся на закладку Advanced и нажимаем кнопку Variables (переменные). Появится окошко с двумя списками переменных. В левом списке выделяем пункт «Количество лейкоцитов», а в правом — пункт «Количество пациентов». Жмем ОК, затем еще раз ОК и получаем график. Заметьте: график является составной частью рабочей книги Workbook, как это ранее было с итоговой таблицей анализа Frequency Tables.
График распределения, построенный с помощью программы STATISTICA
Если кликнуть один раз по любой части получившегося графика правой кнопкой мыши и из контекстного меню выбрать пункт Copy Graph, можно скопировать его в буфер обмена и затем вставить в документ какого-либо другого Windows-приложения, например, MS Word или Excel. График можно сохранить также как самостоятельный файл (с расширением .stg). Для этого необходимо выделить иконку графика в каталоге рабочей книги и, удерживая нажатой левую клавишу мыши, перетащить ее за пределы рабочей книги. В результате график окажется в отдельном окошке. Теперь, кликнув по нему правой кнопкой мыши, можно применить команду Save Graph (сохранить график).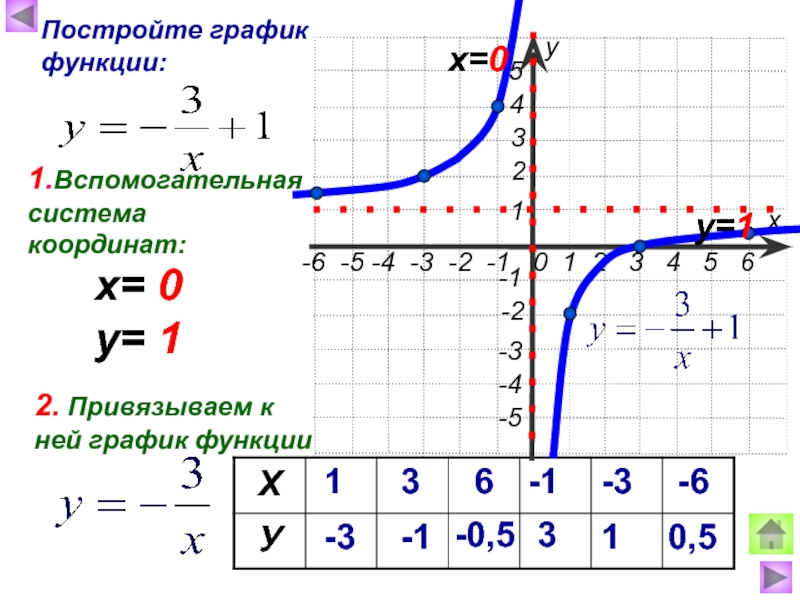
Программа STATISTICA предоставляет огромные возможности для придания графику необходимого внешнего вида. Достаточно кликнуть по интересующему вас элементу, и появится окошко со множеством опций по его преобразованию (заголовок, оси и их названия, маркеры, их форма, цвет и размер, и т.п.).
ПОСТРОЕНИЕ ГИСТОГРАММЫ
Ниже представлены данные о температуре тела пациентов с перитонитом (в °С):
Размах значений температуры тела составляет 38,6 – 35,3 = 3,3. Для графического изображения частотного распределения в данном случае лучше подходит гистограмма, а не график распределения.
Откройте файл «Распределение.sta» и добавьте в него еще одну переменную после столбца «Количество пациента» (как это сделать см. выше) и назовите ее «температура». Введите в этот новый столбец данные о температуре тела пациентов. Далее для построения гистограммы выполните следующие действия:
В основном меню Graphs выберите 2D Graphs > Histograms (Гистограммы).
В появившемся окне выберите закладку Advanced. Нажав на кнопку Variables, выберите для анализа переменную «Температура». В поле Fit type (Тип подгонки) выберите Off, а в выпадающем меню Y axis (Ось Y) — %. Остальные настройки оставьте без изменений.
Нажмите кнопку OK. В результате у вас должен получиться график, подобный приведенному на рисунке:
Гистограмма, построенная с помощью программы STATISTICA.
laquo;Распределение.sta
Добавление комментариев доступно только зарегистрированным пользователям
Графическое
представление информации бывает весьма полезным именно в силу своей
наглядности. 1. График строят на бумаге,
размеченной сеткой. Для ученических практических работ лучше всего брать
миллиметровую бумагу. 2. Особо следует сказать о размере графика: он определяется
не размером имеющегося у вас кусочка «миллиметровки», а масштабом. Масштаб
выбирают прежде всего с учетом интервалов измерения (по каждой оси он
выбирается отдельно). 3. Если планируете некую количественную обработку данных по графику, то экспериментальные точки надо наносить настолько «просторно», чтобы абсолютные погрешности величин можно было изобразить отрезками достаточно заметной длины. Погрешности в этом случае отображают на графиках отрезками, пересекающимися в экспериментальной точке, либо прямоугольниками с центром в экспериментальной точке. Их размеры по каждой из осей должны соответствовать выбранным масштабам. Если погрешность по одной из осей (или по обеим осям) оказывается слишком малой, то предполагается, что она отображается на графике размером самой точки. 4. По горизонтальной оси откладывают значения аргумента, по вертикальной — значения функции. Чтобы различать линии, можно одну проводить сплошной, другую — пунктирной, третью — штрихпунктирной и т.п. Допустимо выделять линии различным цветом. Вовсе не обязательно, чтобы в точке пересечения осей было начало координат 0:0). По каждой из осей можно отображать только интервалы измерения исследуемых величин. 5. Когда приходится откладывать по оси «длинные», многозначные числа, лучше множитель, указывающий порядок числа, учитывать при записи обозначения. 6. На тех участках графика, где имеются некие особенности, такие как резкое изменение кривизны, максимум , минимум, перегиб и др. 7. В ряде случаев удобно пользоваться функциональными масштабами. В этих случаях на осях откладывают не сами измеряемые величины, а функции этих величин. 8. Проводить линию «на глаз» по экспериментальным точкам всегда довольно сложно, наиболее простым случаем, в этом смысле, является проведение прямой. Поэтому посредством удачного выбора функционального масштаба можно привести зависимость к линейной. 9. Графики обязательно нужно подписывать. Подпись должна отражать содержание графика. Следует объяснить в подписи либо основном тексте изображенные на графике линии. 10. Экспериментальные точки, как правило, не соединяются между собой ни отрезками прямой, ни произвольной кривой. Вместо этого строится теоретический график той функции (линейной, квадратичной, экспоненциальной, тригонометрической и т.д.), которая отражает проявляющуюся в данном опыте известную или предполагаемую физическую закономерность, выраженную в виде соответствующей формулы. 11. В лабораторном практикуме встречаются два случая: проведение теоретического графика преследует цель извлечения из эксперимента неизвестных параметров функции (тангенса угла наклона прямой, показателя экспоненты и т.д.), либо делается сравнение предсказаний теории с результатами эксперимента. 12. В первом случае график соответствующей функции проводится «на глаз» так, чтобы он проходил по всем областям погрешности возможно ближе к экспериментальным точкам. Существуют математические методы, позволяющие провести теоретическую кривую через экспериментальные точки в определенном смысле наилучшим образом. При проведении графика «на глаз» рекомендуется пользоваться зрительным ощущением равенства нулю суммы положительных и отрицательных отклонений точек от проводимой кривой. 13. Во втором случае график строится по результатам расчетов, причем расчетные значения находятся не только для тех точек, которые были получены в опыте, а с некоторым шагом по всей области измерений для получения плавной кривой. Нанесение на миллиметровку результатов расчетов в виде точек является рабочим моментом — после проведения теоретической кривой эти точки с графика убираются. Если в расчетную формулу входит уже определенный (или заранее известный) экспериментальный параметр, то расчеты проводятся как со средним значением параметра, так и с его максимальным и минимальным (в пределах погрешности) значениями. На графике в этом случае изображается кривая, полученная со средним значением параметра, и полоса, ограниченная двумя расчетными кривыми для максимального и минимального значений параметра. 1. http://iatephysics.narod.ru/knowhow/knowhow7.htm 2. Мацукович Н.А., Слободянюк А.И. Физика: рекомендации к лабораторному практикуму. Минск, БГУ, 2006 г. |
Построение диаграмм на Python с помощью Matplotlib
Бывает, что нужно по-быстрому визуализировать какие-то данные — построить графики для презентации или вроде того. Есть много способов сделать это. Например, можно открыть CSV-файл в LibreOffice или Google Docs и построить графики в нем. Но что, если диаграммы нужно строить регулярно, а значит предпочтительнее делать это автоматически? Вот тут-то на помощь и приходит Python с его потрясающей библиотекой Matplotlib.
Примечание: Для решения той же задачи в свое время мне доводилось использовать Scala Chart. Однако, как вы сами сейчас убедитесь, Matplotlib куда гибче, да и графики у него получаются намного красивее. Если вас интересует тема визуализации данных, вам стоит обратить внимание на мои стары посты, посвященные Graphviz, а также JavaScript-библиотекам Flot и Dracula.
Не будем ходить вокруг да около, лучше сразу перейдем к примерам. Пожалуй, простейший график, который можно построить в Matplotlib, это график синуса и косинуса:
Пожалуй, простейший график, который можно построить в Matplotlib, это график синуса и косинуса:
# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.axis([0, 10, -1.5, 1.5])
plt.title(‘Sine & Cosine’)
plt.xlabel(‘x’)
plt.ylabel(‘F(x)’)
xs = []
sin_vals = []
cos_vals = []
x = 0.0
while x < 10.0:
sin_vals += [ math.sin(x) ]
cos_vals += [ math.cos(x) ]
xs += [x]
x += 0.1
plt.plot(xs, sin_vals, color = ‘blue’, linestyle = ‘solid’,
label = ‘sin(x)’)
plt.plot(xs, cos_vals, color = ‘red’, linestyle = ‘dashed’,
label = ‘cos(x)’)
plt.legend(loc = ‘upper right’)
fig.savefig(‘trigan.png’)
Я думаю, что код не нуждается в пояснениях. В крайнем случае, вы можете полистать официальную документацию или почитать вывод help() в REPL’е.
Получившийся график:
Однако на практике часто нужно построить график функции не от абстрактного вещественного числа, а от вполне конкретного времени. И в этом случае хочется, чтобы по оси OX были подписаны не абстрактные 1, 2, 3, а вполне конкретные временные метки. Для примера рассмотрим построение графика регистрации новых доменов в зоне RU за разное время с разбивкой по регистраторам:
#!/usr/bin/env python3# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
dates = []
values = {}
with open(‘ru-newreg.csv’, newline = ») as f:
for row in csv.reader(f, delimiter = ‘,’, quotechar = ‘»‘):
if dates == []:
dates = [
dt.datetime.strptime(
«{}-01».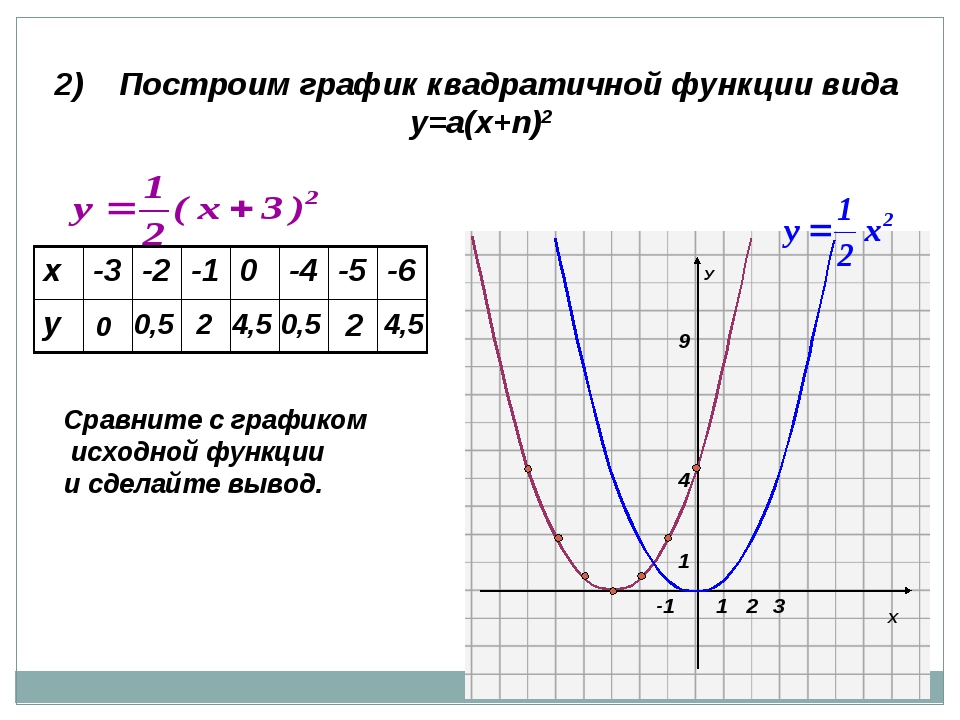 format(d),
format(d),
‘%Y-%m-%d’
).date()
for d in row[1:]
]
continue
values[ row[0] ] = row[1:]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.title(‘RU New Domain Names Registration’)
plt.xlabel(‘Year’)
plt.ylabel(‘Domains’)
ax = plt.axes()
ax.yaxis.grid(True)
ax.xaxis.set_major_formatter(mdates.DateFormatter(‘%Y’))
ax.xaxis.set_major_locator(mdates.YearLocator())
for reg in values.keys():
plt.plot(dates, values[reg], linestyle = ‘solid’, label = reg)
plt.legend(loc=’upper left’, frameon = False)
fig.savefig(‘domains.png’)
Данные были получены с ныне уже закрытого сайта stat.nic.ru, который, впрочем, все еще доступен на web.archive.org. Результирующий график:
Что еще часто строят, это столбчатые диаграммы. В качестве примера возьмем данные из заметки Поиск по географическим данным при помощи PostGIS и построим диаграмму, отображающую сколько точек на карте к какому типу (заправка, кафе и так далее) относятся. Чтобы было чуть интереснее, сделаем вид, что в прошлом году точек каждого вида было на 10% меньше, и попытаемся отразить это изменение:
#!/usr/bin/env python3# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘cafe’, ‘pharmacy’, ‘fuel’, ‘bank’, ‘waste_disposal’,
‘atm’, ‘bench’, ‘parking’, ‘restaurant’,
‘place_of_worship’]
data_values = [9124, 8652, 7592, 7515, 7041, 6487, 6374, 6277,
5092, 3629]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 10})
plt.title(‘OpenStreetMap Point Types’)
ax = plt.axes()
ax. yaxis.grid(True, zorder = 1)
yaxis.grid(True, zorder = 1)
xs = range(len(data_names))
plt.bar([x + 0.05 for x in xs], [ d * 0.9 for d in data_values],
width = 0.2, color = ‘red’, alpha = 0.7, label = ‘2016’,
zorder = 2)
plt.bar([x + 0.3 for x in xs], data_values,
width = 0.2, color = ‘blue’, alpha = 0.7, label = ‘2017’,
zorder = 2)
plt.xticks(xs, data_names)
fig.autofmt_xdate(rotation = 25)
plt.legend(loc=’upper right’)
fig.savefig(‘bars.png’)
Результат:
Те же данные можно отобразить, расположив столбики горизонтально:
#!/usr/bin/env python3# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘cafe’, ‘pharmacy’, ‘fuel’, ‘bank’, ‘w.d.’, ‘atm’,
‘bench’, ‘parking’, ‘restaurant’, ‘p.o.w.’]
data_values = [9124, 8652, 7592, 7515, 7041, 6487, 6374, 6277,
5092, 3629]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 9})
plt.title(‘OpenStreetMap Point Types’)
ax = plt.axes()
ax.xaxis.grid(True, zorder = 1)
xs = range(len(data_names))
plt.barh([x + 0.3 for x in xs], [ d * 0.9 for d in data_values],
height = 0.2, color = ‘red’, alpha = 0.7, label = ‘2016’,
zorder = 2)
plt.barh([x + 0.05 for x in xs], data_values,
height = 0.2, color = ‘blue’, alpha = 0.7, label = ‘2017’,
zorder = 2)
plt.yticks(xs, data_names, rotation = 10)
plt.legend(loc=’upper right’)
fig.savefig(‘barshoris.png’)
Соответствующая диаграмма:
И последний на сегодня вид диаграмм — круговая диаграмма, или «пирог». Для примера попробуем визуализировать распределение кафе по различным городам России:
#!/usr/bin/env python3# vim: set ai et ts=4 sw=4:
import matplotlib as mpl
import matplotlib. pyplot as plt
pyplot as plt
import matplotlib.dates as mdates
import datetime as dt
import csv
data_names = [‘Москва’, ‘Санкт-Петербург’, ‘Сочи’, ‘Архангельск’,
‘Владимир’, ‘Краснодар’, ‘Курск’, ‘Воронеж’,
‘Ставрополь’, ‘Мурманск’]
data_values = [1076, 979, 222, 189, 137, 134, 124, 124, 91, 79]
dpi = 80
fig = plt.figure(dpi = dpi, figsize = (512 / dpi, 384 / dpi) )
mpl.rcParams.update({‘font.size’: 9})
plt.title(‘Распределение кафе по городам России (%)’)
xs = range(len(data_names))
plt.pie(
data_values, autopct=’%.1f’, radius = 1.1,
explode = [0.15] + [0 for _ in range(len(data_names) — 1)] )
plt.legend(
bbox_to_anchor = (-0.16, 0.45, 0.25, 0.25),
loc = ‘lower left’, labels = data_names )
fig.savefig(‘pie.png’)
Полученная круговая диаграмма:
Выше была рассмотрена лишь малая часть возможностей Matplotlib. Чтобы получить более полное представление о всей мощи этой библиотеки, советую заглянуть в галерею построенных с ее помощью графиков на официальном сайте. Что же до исходников к этому посту, как обычно, вы найдете их на GitHub.
А чем вы строите диаграммы и, если не секрет, как они при этом выглядят?
Дополнение: См также заметки Примеры использования Python-библиотеки NumPy, Визуализация проведенных радиосвязей с помощью Matplotlib и Basemap и Рисуем диаграммы Вольперта-Смита на Python.
Метки: Python.
График по точкам
Решения уравнений с двумя переменными
Линейное уравнение с двумя переменными Уравнение с двумя переменными, которое может быть записано в стандартной форме ax + by = c, где действительные числа a и b не равны нулю. имеет стандартную форму ax + by = c, где a , b и c — действительные числа, а a и b не равны 0. Решения уравнений этой формы представляют собой упорядоченные пары ( x , и ), где координаты при подстановке в уравнение дают истинное утверждение.
Пример 1: Определите, являются ли (1, −2) и (−4, 1) решениями для 6x − 3y = 12.
Решение: Подставьте значения x и y в уравнение, чтобы определить, дает ли упорядоченная пара истинное утверждение.
Ответ: (1, −2) — решение, а (−4, 1) — нет.
Часто бывает, что линейное уравнение задается в форме, в которой одна из переменных, обычно y , изолирована.Если это так, то мы можем проверить, является ли упорядоченная пара решением, подставив значение одной из координат и упростив, чтобы увидеть, получим ли мы другую.
Пример 2: Являются ли (12, −3) и (−5, 14) решениями y = 2x − 4?
Решение: Замените значения x и упростите, чтобы увидеть, получены ли соответствующие значения y .
Ответ: (12, −3) — решение, а (−5, 14) — нет.
Попробуй! Является ли (6, −1) решением y = −23x + 3?
Ответ: Да
Если даны линейные уравнения с двумя переменными, мы можем решить для одной из переменных, обычно и , и получить эквивалентное уравнение следующим образом:
В этой форме мы видим, что y зависит от x . Здесь x — это независимая переменная, которая определяет значения других переменных.Обычно мы думаем о значении x как о независимой переменной. и y — зависимая переменная Переменная, значение которой определяется значением независимой переменной. Обычно мы воспринимаем значение y как зависимую переменную.
Линейное уравнение y = 2x − 4 можно использовать для нахождения упорядоченных парных решений. Если мы заменим x любым действительным числом, то можно упростить поиск соответствующего значения y . Например, если x = 3, то y = 2 (3) −4 = 6−4 = 2, и мы можем сформировать упорядоченное парное решение (3, 2). Поскольку для x можно выбрать бесконечно много действительных чисел, линейное уравнение имеет бесконечно много упорядоченных парных решений ( x , y ).
Например, если x = 3, то y = 2 (3) −4 = 6−4 = 2, и мы можем сформировать упорядоченное парное решение (3, 2). Поскольку для x можно выбрать бесконечно много действительных чисел, линейное уравнение имеет бесконечно много упорядоченных парных решений ( x , y ).
Пример 3: Найдите упорядоченные парные решения уравнения 5x − y = 14 с заданными значениями x {−2, −1, 0, 4, 6}.
Решение: Сначала решите относительно и .
Затем подставьте значения x в уравнение y = 5x − 14, чтобы найти соответствующие значения y .
Ответ: {(−2, −24), (−1, −19), (0, −14), (4, 6), (6, 16)}
В предыдущем примере даны определенные значения x , но это не всегда так. Рассматривая x как независимую переменную, мы можем выбрать любые значения для x , а затем подставить их в уравнение, чтобы найти соответствующие значения y .Этот метод дает столько упорядоченных парных решений, сколько мы пожелаем.
Пример 4: Найдите пять упорядоченных парных решений уравнения 6x + 2y = 10.
Решение: Сначала решите относительно и .
Затем выберите любой набор значений x . Обычно мы выбираем некоторые отрицательные значения и некоторые положительные значения. В этом случае мы найдем соответствующие значения y , когда x равно {−2, −1, 0, 1, 2}.Сделайте замены, необходимые для заполнения следующей таблицы (часто называемой t-диаграммой):
Ответ: {(−2, 11), (−1, 8), (0, 5), (1, 2), (2, −1)}. Поскольку существует бесконечно много упорядоченных парных решений, ответы могут варьироваться в зависимости от выбора значений для независимой переменной.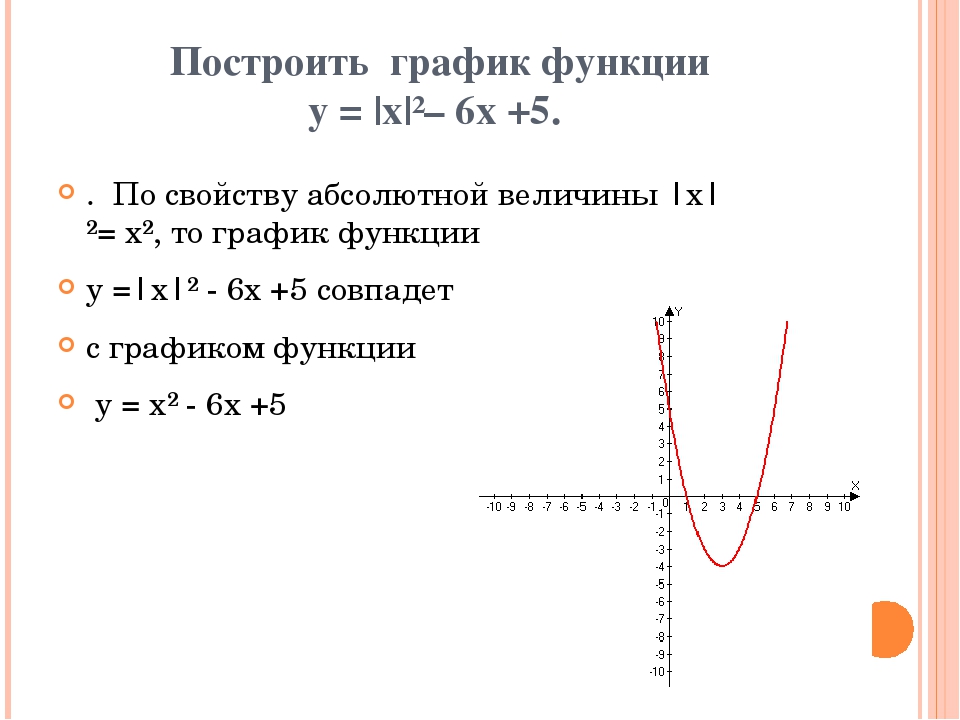
Попробуй! Найдите пять упорядоченных парных решений уравнения 10x − 2y = 2.
Ответ: {(−2, −11), (−1, −6), (0, −1), (1, 4), (2, 9)} ( ответов могут отличаться от )
График по точкам
Поскольку решения линейных уравнений представляют собой упорядоченные пары, их можно построить в виде графиков в прямоугольной системе координат.Набор всех решений линейного уравнения может быть представлен на прямоугольной координатной плоскости с помощью прямой линии, соединяющей по крайней мере две точки; эта линия называется его графиком Точка на числовой прямой, связанной с координатой .. Чтобы проиллюстрировать это, постройте пять упорядоченных парных решений, {(−2, 11), (−1, 8), (0, 5), (1) , 2), (2, −1)}, в линейное уравнение 6x + 2y = 10.
Обратите внимание, что точки коллинеарны; это будет иметь место для любого линейного уравнения.Проведите линию через точки с помощью линейки и добавьте стрелки с обоих концов, чтобы указать, что график продолжается бесконечно.
Получившаяся линия представляет все решения 6x + 2y = 10, которых бесконечно много. Шаги построения линий путем нанесения точек описаны в следующем примере.
Пример 5: Найдите пять упорядоченных парных решений и график: 10x − 5y = 10.
Решение:
Шаг 1: Решить относительно и .
Шаг 2 : Выберите не менее двух значений x и найдите соответствующие значения y . В этом разделе мы выберем пять действительных чисел для использования в качестве значений x . Рекомендуется выбирать 0 и некоторые отрицательные числа, а также некоторые положительные числа.
Пять упорядоченных парных решений: {(−2, −6), (−1, −4), (0, −2), (1, 0), (2, 2)}
Шаг 3: Выберите подходящий масштаб, нанесите точки и проведите через них линию с помощью линейки. В этом случае выберите масштаб, в котором каждая отметка на оси y представляет 2 единицы, поскольку все значения y кратны 2.
В этом случае выберите масштаб, в котором каждая отметка на оси y представляет 2 единицы, поскольку все значения y кратны 2.
Ответ:
Не всегда будет так, что y может быть решено в терминах x с целыми коэффициентами. На самом деле коэффициенты часто оказываются дробными.
Пример 6: Найдите пять упорядоченных парных решений и построите график: −5x + 2y = 10.
Решение:
Помните, что вы можете выбрать любое действительное число для независимой переменной x , так что выбирайте здесь с умом. Поскольку знаменатель коэффициента переменной x равен 2, вы можете избежать дроби, выбрав для значений x числа, кратные 2. В этом случае выберите набор значений x {−6, −4, −2, 0, 2} и найдите соответствующие значения y .
Пять решений: {(−6, −10), (−4, −5), (−2, 0), (0, 5), (2, 10)}.Здесь мы выбираем масштабирование оси x с кратностью 2 и оси y с кратностью 5.
Ответ:
Попробуй! Найдите пять упорядоченных парных решений и график: x + 2y = 6.
Ответ: {(−2, 4), (0, 3), (2, 2), (4, 1), (6, 0)}
Горизонтальные и вертикальные линии
Нам нужно распознать путем осмотра линейные уравнения, которые представляют собой вертикальную или горизонтальную линию.
Пример 7: График из пяти точек: y = −2.
Решение: Поскольку данное уравнение не имеет переменной x , мы можем переписать его с коэффициентом 0 для x .
Выберите любые пять значений для x и убедитесь, что соответствующее значение y всегда равно -2.
Теперь у нас есть пять упорядоченных парных решений для построения графиков {(−2, −2), (−1, −2), (0, −2), (1, −2), (2, −2)}.
Ответ:
Когда коэффициент для переменной x равен 0, график представляет собой горизонтальную линию. В общем, уравнение для горизонтальной линии — это любая линия, уравнение которой можно записать в виде y = k , где k — действительное число. можно записать в виде y = k, где k представляет любое действительное число.
Пример 8: График из пяти точек: x = 3.
Решение: Поскольку данное уравнение не имеет переменной y , перепишите его с коэффициентом 0 для y .
Выберите любые пять значений для y и убедитесь, что соответствующее значение x всегда равно 3.
Теперь у нас есть пять упорядоченных парных решений для построения: {(3, −2), (3, −1), (3, 0), (3, 1), (3, 2)}.
Ответ:
Когда коэффициент для переменной y равен 0, график представляет собой вертикальную линию.В общем, уравнение для вертикальной линии — любая линия, уравнение которой можно записать в виде x = k , где k — действительное число. можно записать как x = k, где k представляет любое действительное число.
Подводя итог, если k — действительное число,
Попробуй! Изобразите y = 5 и x = −2 на одном и том же наборе осей и определите, где они пересекаются.
Ответ: (−2, 5)
Основные выводы
- Решения линейных уравнений с двумя переменными ax + by = c представляют собой упорядоченные пары ( x , y ), где координаты при подстановке в уравнение приводят к истинному утверждению.

- Линейные уравнения с двумя переменными имеют бесконечно много упорядоченных парных решений. Когда решения нанесены на график, они коллинеарны.
- Чтобы найти упорядоченные парные решения, выберите значения для независимой переменной, обычно x , и подставьте их в уравнение, чтобы найти соответствующие значения y .
- Чтобы построить график линейных уравнений, определите по крайней мере два упорядоченных парных решения и проведите через них линию линейкой.
- Горизонтальные линии описываются как y = k , где k — любое действительное число.
- Вертикальные линии описываются как x = k , где k — любое действительное число.
Тематические упражнения
Часть A: Решения для линейных систем
Определить, является ли данная точка решением.
1.5x − 2y = 4; (-1, 1)
2. 3x − 4y = 10; (2, −1)
3. −3x + y = −6; (4, 6)
4. −8x − y = 24; (−2, −3)
5. −x + y = −7; (5, −2)
6. 9x − 3y = 6; (0, −2)
7. 12x + 13y = −16; (1, −2)
8. 34x − 12y = −1; (2, 1)
9. 4x − 3y = 1; (12, 13)
10. −10x + 2y = −95; (15, 110)
11. y = 13x + 3; (6, 3)
12.у = −4x + 1; (-2, 9)
13. y = 23x − 3; (0, −3)
14. y = −58x + 1; (8, −5)
15. y = −12x + 34; (−12, 1)
16. y = −13x − 12; (12, −23)
17. y = 2; (−3, 2)
18. y = 4; (4, −4)
19. х = 3; (3, −3)
20. х = 0; (1, 0)
Найдите упорядоченные парные решения для набора x -значений.
21. y = −2x + 4; {−2, 0, 2}
22. y = 12x − 3; {−4, 0, 4}
23. y = −34x + 12; {−2, 0, 2}
24. y = −3x + 1; {−1/2, 0, 1/2}
25. y = −4; {−3, 0, 3}
26. y = 12x + 34; {−1/4, 0, 1/4}
27. 2x − 3y = 1; {0, 1, 2}
28. 3x − 5y = −15; {−5, 0, 5}
29. –x + y = 3; {−5, −1, 0}
30. 12x − 13y = −4; {−4, −2, 0}
31.35х + 110у = 2; {−15, −10, −5}
32. х-у = 0; {10, 20, 30}
Найдите упорядоченные парные решения, учитывая набор значений и .
33. y = 12x − 1; {−5, 0, 5}
34. y = −34x + 2; {0, 2, 4}
35. 3x − 2y = 6; {−3, −1, 0}
36. −x + 3y = 4; {−4, −2, 0}
37. 13x − 12y = −4; {−1, 0, 1}
38. 35х + 110у = 2; {−20, −10, −5}
Часть B: Графические линии
Учитывая набор x -значений {−2, −1, 0, 1, 2}, найдите соответствующие значения y и изобразите их на графике.
39. у = х + 1
40. у = −x + 1
41. у = 2х − 1
42. у = −3x + 2
43. у = 5х − 10
44. 5x + y = 15
45. 3x − y = 9
46. 6x − 3y = 9
47. y = −5
48. y = 3
Найдите как минимум пять упорядоченных парных решений и график.
49. у = 2х − 1
50.у = −5x + 3
51. у = −4x + 2
52. у = 10х − 20
53. у = −12x + 2
54. у = 13x − 1
55. y = 23x − 6
y = 23x − 6
56. у = −23x + 2
57. у = х
58. y = −x
59. −2x + 5y = −15
60. х + 5у = 5
61. 6x − y = 2
62. 4x + y = 12
63. −x + 5y = 0
64.х + 2у = 0
65. 110x − y = 3
66. 32x + 5y = 30
Часть C: Горизонтальные и вертикальные линии
Найдите не менее пяти упорядоченных парных решений и нанесите их на график.
67. y = 4
68. y = −10
69. х = 4
70. х = -1
71. y = 0
72. х = 0
73. y = 34
74.х = -54
75. Постройте линии y = −4 и x = 2 на одном и том же наборе осей. Где они пересекаются?
76. Постройте линии y = 5 и x = −5 на одном и том же наборе осей. Где они пересекаются?
77. Какое уравнение описывает ось x ?
78. Какое уравнение описывает ось y ?
Часть D: Смешанная практика
График по точкам.
79. y = −35x + 6
80. y = 35x − 3
81. у = −3
82. х = −5
83. 3x − 2y = 6
84. −2x + 3y = −12
Часть E: Темы дискуссионной доски
85. Обсудите значение связи между алгеброй и геометрией при описании линий.
86. Приведите реальные примеры, связанные с двумя неизвестными.
ответов
1: Нет
3: Есть
5: Есть
7: Есть
9: Есть
11: Нет
13: Есть
15: Есть
17: Есть
19: Есть
21: {(−2, 8), (0, 4), (2, 0)}
23: {(−2, 2), (0, 1/2), (2, −1)}
25: {(−3, −4), (0, −4), (3, −4)}
27: {(0, −1/3), (1, 1/3), (2, 1)}
29: {(−5, −2), (−1, 2), (0, 3)}
31: {(-15, 110), (-10, 80), (-5, 50)}
33: {(−8, −5), (2, 0), (12, 5)}
35: {(0, −3), (4/3, −1), (2, 0)}
37: {(−27/2, −1), (−12, 0), (−21/2, 1)}
39:
41:
43:
45:
47:
49:
51:
53:
55:
57:
59:
61:
63:
65:
67:
69:
71:
73:
75:
77: y = 0
79:
81:
83:
| Алгоритм компоновки — один из: «ациклический», «круговой» (строит граф с вершинами, равномерно распределенными по окружности), «ранжированный», «графвиз», «планарный», «пружинный» (традиционная компоновка пружин, с использованием текущие позиции графика как начальные позиции) или «дерево» (дерево будет построено по уровням, в зависимости от минимального расстояния до корня). |
| Число раз для выполнения алгоритма компоновки пружины. |
| Словарь, отображающий высоты в список вершин на этой высоте. |
| Используйте пружинный макет, чтобы завершить текущий макет. |
| Обозначение вершины для рисования деревьев. Вершина дерева, которая будет использоваться в качестве корня для опции |
| Итерация, определяющая, какие вершины использовать в качестве корней для параметра |
| Направление ветвей дерева — «вверх», «вниз», «влево» или «вправо». |
| Сохранять или нет вычисленное положение для графика. |
| Размер макета — 2 или 3. |
| Какую программу компоновки graphviz использовать — одну из «circo», «dot», «fdp», «neato» или «twopi». |
| Делать ли компоновку пружины связным компонентом — логическое значение. |
| Позиционный словарь вершин |
| Следует ли рисовать метки вершин. |
| Цвет по умолчанию для вершин, не перечисленных в словаре vertex_colors. |
| Словарь раскраски вершин: каждый ключ — это цвет, распознаваемый matplotlib, и каждая соответствующая запись представляет собой список вершин. |
| Размер для рисования вершин. |
| Форма для рисования вершин. В настоящее время недоступен для многогранных диаграмм. |
| Следует ли рисовать краевые метки. |
| Стиль линий краев.Это должно быть одно из следующих значений: «сплошной», «пунктирный», «пунктирный», «тире» или «-», «-», «:», «-.» Соответственно. |
| Толщина кромки. |
| Цвет по умолчанию для краев, не перечисленных в edge_colors. |
| словарь, определяющий цвета краев: каждый ключ — это цвет, распознаваемый matplotlib, и каждая запись представляет собой список краев. |
| Следует ли раскрашивать края в соответствии с их этикетками. Это также принимает функцию или словарь, отображающий метки в цвета. |
| Разбиение множества вершин. Если указано, на графике каждая ячейка будет отображаться другим цветом. vertex_colors имеет приоритет. |
| Радиус наименьшей петли. |
| Расстояние между многолезвиями. |
| Максимальный диапазон расстояний, позволяющий использовать несколько ребер. |
| Отображать ли вершины в режиме разговора (большие и белые). |
| Следует ли рисовать рамку вокруг графика. |
| Цвет фона кромки метки |
Построение линейных графиков
|
Использование Microsoft Excel для построения графика
Использование Microsoft Excel для построения графика Использование Microsoft Excel для построения графика Построение набора данных X-YПредположим, мы хотим построить график зависимости объема использованной соляной кислоты отродинки магний.
1. Первым шагом в создании графика с помощью Microsoft Excel является ввод данных. Данные должны быть в двух соседних столбцах с данными x слева. столбец. Столбцы должны быть помечены в первой строке, чтобы определить, какие числа в Таблицу представляют. (рисунок 4).
Рисунок 4: Данные по осям X и Y
2. Поместите курсор на первое значение X (т.е.е., вверху
столбец, содержащий значения x или значения «Молей Mg»), удерживайте левую часть
кнопку мыши и перетащите курсор мыши к нижнему значению Y (т. е. внизу
столбец, содержащий значения y или значения «Объем HCl»). Все X-Y
значения должны быть выделены (рисунок 4).
е. внизу
столбец, содержащий значения y или значения «Объем HCl»). Все X-Y
значения должны быть выделены (рисунок 4).
3. Щелкните Вставить в верхнем левом углу панели инструментов.
4. Нажмите на диаграмму
5. Щелкните поле с надписью XY (Scatter) .
6. Щелкните Далее> .
7. Щелкните шаблон X-Y без линий (вариант формата 1).
8. Щелкните Далее> ; уменьшенная версия вашего появится график.
9. Щелкните Далее> .
10. Щелкните прямоугольное поле с надписью «Заголовок диаграммы» и введите название графика (например,g., «Объем HCl относительно молей Mg).
11. Щелкните отдельно поля с надписью «Категория ( X )» и «Значение ( Y )» и введите метку для оси X (например, Moles Mg) и Ось Y (например, объем HCl (мл)).
12. Щелкните Как новый лист . Это проинструктирует программа для отображения данных на отдельном листе с надписью «Chart1».
13. Щелкните Далее> .
14. Нажмите Готово . На этом этапе у вас будет создал график X-Y данных, который должен выглядеть, как на рисунке 5.
Рисунок 5: X-Y график экспериментальных данных
окон — Хорошее приложение для построения графиков
окно — Хорошее приложение для построения графиков — СуперпользовательСеть обмена стеками
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Подписаться
Super User — это сайт вопросов и ответов для компьютерных энтузиастов и опытных пользователей.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 851 раз
Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.
Это вопрос не по теме. В настоящее время он не принимает ответы.Хотите улучшить этот вопрос? Обновите вопрос, чтобы он был по теме для суперпользователя.
Закрыт 4 года назад.
Кто-нибудь знает о бесплатном приложении для построения графиков для Windows (или онлайн-инструменте), которое может строить что-то вроде этого?
ГаффХ n + 1 = r sin (π * X n )
17.4k1414 золотых знаков5353 серебряных знака6767 бронзовых знаков
Создан 14 окт.
Нифле32.6k2525 золотых знаков103103 серебряных знака136136 бронзовых знаков
Я хотел бы предложить WolframAlpha, но у него проблемы с «r *».Лучшее, что я мог сделать, это это.
Гафф17.4k1414 золотых знаков5353 серебряных знака6767 бронзовых знаков
Создан 14 окт.
синфосинфо1,
золотых знаков1111 серебряных знаков1313 бронзовых знаков
3 Я бы попробовал Gnuplot или Octave / Matlab. Если бы у вас был Apple, встроенный Grapher справился бы с этой задачей.
Если бы у вас был Apple, встроенный Grapher справился бы с этой задачей.
17.4k1414 золотых знаков5353 серебряных знака6767 бронзовых знаков
Создан 14 окт.
Бастибебастиб3,66299 золотых знаков3030 серебряных знаков4343 бронзовых знака
1Попробуйте Graph Ивана Йохансена.
ГаффGraph — это приложение с открытым исходным кодом, используемое для рисования математических графиков. в системе координат. Всем, кто хочет рисовать графики функций сочтёт эту программу полезной. Программа позволяет очень легко визуализировать функцию и вставить ее в другую программу. Это также можно сделать некоторые математические вычисления на функциях.
17.4k1414 золотых знаков5353 серебряных знака6767 бронзовых знаков
Создан 24 окт.
пользователь 259774727111 серебряный знак66 бронзовых знаков
Я бы порекомендовал matplotlib (требуются некоторые базовые знания Python).
matplotlib — это библиотека 2D-построения на Python, которая производит публикацию показатели качества в различных форматах бумажных и интерактивных среды на разных платформах.
matplotlib можно использовать в python скрипты, оболочка python и ipython (ala MATLAB® или Mathematica®), серверы веб-приложений и шесть наборов инструментов графического пользовательского интерфейса.
Документация все еще находится в стадии разработки, поэтому освоение MPL может занять некоторое время, но, очевидно, оно того стоит, если вы взглянете на приведенные здесь примеры.
Гафф17.4k1414 золотых знаков5353 серебряных знака6767 бронзовых знаков
Создан 15 янв.
Мило Велондек88111 золотой знак1212 серебряных знаков2222 бронзовых знака
Не тот ответ, который вы ищете? Просмотрите другие вопросы с тегами диаграммы Windows или задайте свой вопрос.
Суперпользователь лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Топ-5 лучших Python-библиотек для построения графиков и графиков
В этой статье рассказывается о некоторых из лучших Python-библиотек для построения графиков и графиков! Прежде чем мы начнем со списка лучших библиотек, давайте кратко рассмотрим, зачем нужна визуализация данных и что
Зачем нужна визуализация данных?
В эпоху бурного развития анализа данных часто удобнее просматривать результаты нашего анализа и делать выводы, чем просматривать текстовые данные или файлы csv, чтобы понять результаты.
Следовательно, визуализация данных — это простой способ найти ответы на сложные вопросы. Это также позволяет пользователям выражать результаты лучше, чем таблицы.
Визуализация данныхТоп-5 лучших Python-библиотек для построения графиков и графиков
Вот краткий список нескольких Python для построения графиков и библиотек графиков, которые мы обсудим:
- Matplotlib: Простое построение графиков для всех приложений, использующих его API.
- Seaborn: Универсальная библиотека на основе matplotlib, которая позволяет сравнивать несколько переменных.
- ggplot: Создает визуализацию для конкретных областей
- Bokeh: Предпочтительные библиотеки для потоковой передачи и данных в реальном времени.
- Plotly: Позволяет создавать очень интерактивные графики с помощью JS.
1. Matplotlib
МатплотлибMatplotlib — это библиотека построения графиков для Python. Он предоставляет объектно-ориентированный API, который позволяет нам строить графики в самом приложении. Это бесплатно и с открытым исходным кодом. Поддерживает десятки типов вывода и серверную часть.
Matplotlib позволяет использовать pandas в качестве оболочки для своего API. Эта библиотека имеет лучшее время выполнения и занимает мало места в памяти.
Преимущества использования Matplotlib
- Понимание корреляции между переменными
- Сообщает подгонку данных модели
- Диаграммы разброса могут использоваться для обнаружения выбросов
2. Seaborn
СиборнSeaborn — это библиотека визуализации данных, доступная на Python, основанная на matplotlib.У Seaborn есть API, основанный на наборах данных, позволяющих сравнивать несколько переменных.
Он поддерживает многослойные сетки, которые, в свою очередь, упрощают построение сложной визуализации. В нем доступны одномерные и двумерные визуализации для сравнения подмножеств данных.
Он использует разные цветовые палитры для выявления различных типов узоров. Он также автоматически оценивает модели линейной регрессии.
Seaborn против Matplotlib
Matplotlib пытается упростить простые вещи, а сложные — возможными, seaborn также пытается легко определить четко определенный набор сложных вещей.На самом деле matplotlib хорош, но seaborn лучше. Matplotlib оставляет графики менее привлекательными, но seaborn имеет высокоуровневые интерфейсы и настраиваемые темы для решения этой проблемы.
При работе с пандами matplotlib плохо работает при работе с фреймами данных. В то время как функции seaborn работают с фреймами данных.
3. ggplot
GgplotПервоначально реализованный в R, ggplot — одна из универсальных библиотек для построения графиков в Python. Это предметно-ориентированный язык для создания визуализаций, зависящих от предметной области, особенно для анализа данных.
Ggplot позволяет построить график простым способом, используя всего 2 строки кода. Однако тот же код, написанный с использованием matplotlib, очень сложен и включает в себя много строк кода. Следовательно, ggplot упрощает кодирование графика. Это чрезвычайно ценная библиотека Python.
Необходимо использовать pandas для достижения всех возможностей ggplot.
4. Боке
БокеBokeh, библиотека, похожая на ggplot, основана на Грамматике графики.Однако это родная для python библиотека, которая не была импортирована из R. Создает интерактивные веб-графики, которые можно выводить в различных форматах, таких как — документы HTML и объекты JSON.
Bokeh — одна из самых популярных библиотек для потоковой передачи и передачи данных в реальном времени.
Bokeh доступно для пользователей в трех уровнях, а именно — высокий уровень, средний уровень и низкий уровень. Пользователи высокого уровня могут легко и быстро создавать гистограммы и гистограммы. Пользователи среднего уровня могут использовать структуру matplotlib для создания точек для диаграмм разброса.
5. Сюжет
СюжетноPlotly — это онлайн-платформа для визуализации с поддержкой библиотеки. Здесь мы можем создавать интерактивные графики так же, как Bokeh, но с дополнительными графиками, такими как контурные графики, трехмерные диаграммы и дендрограммы. Plotly также распознает события наведения указателя мыши и щелчка курсора, что делает Plotly уникальной библиотекой как с графикой, так и с JavaScript.
Bokeh и Plotly — похожие библиотеки, однако с Plotly вам придется конвертировать данные в словари.Однако plotly проще, когда дело доходит до обработки фреймов данных с помощью Pandas.
Подводя итог…
Использование Python для построения графиков выгодно и невыгодно по той простой причине, что Python предлагает широкий спектр возможностей. Выбор лучшей библиотеки полностью зависит от типа задачи, которую вы пытаетесь выполнить. Обратите внимание: ни одна библиотека не превосходит другую, и использование каждой библиотеки зависит от потребностей пользователя.
Matplotlib, однако, служит ядром всех этих библиотек и позволяет кодерам оборачивать их инструментами.Seaborn, используя matplotlib, строит сложные интерактивные визуализации. С другой стороны, боке помогает создать собственный сервер для визуализаций. Используйте эти библиотеки и дайте нам знать, что вы чувствуете, в разделе комментариев ниже.
Python рисование — документация Matplotlib 3.3.4
Matplotlib — это комплексная библиотека для создания статических, анимированных, и интерактивные визуализации на Python.
Matplotlib упрощает легкие, а сложные — возможными.
Присоединяйтесь к нашему сообществу! ¶
Matplotlib — гостеприимный, инклюзивный проект, и мы следуем Python Кодекс поведения Software Foundation во всем, что мы делаем.
Получить помощь
Если у вас есть вопросы, обязательно ознакомьтесь с FAQ, документы API. Полный текст поиск — хороший способ найти документацию, включая множество примеров.
Новости
Чтобы быть в курсе того, что происходит в Matplotlib, см. какая новая страница или просмотрите исходный код. Все, что могло требовать изменений в существующем коде регистрируется в API изменяет файл.
Разработка
Matplotlib размещен на GitHub.
Будет хорошей идеей также связаться с нами по Discourse.
Списки рассылки
Цитирование Matplotlib¶
Матплотлиб — детище Джона Хантера (1968-2012), который вместе со своими многие участники потратили неизмеримое количество времени и усилий на создание программного обеспечения, используемого тысячами ученых по всему миру.
Если Matplotlib участвует в проекте, который ведет к научной публикации, пожалуйста, подтвердите эту работу, цитируя проект.Готовая цитата запись доступна.
Открытый исходный код¶
Matplotlib — спонсируемый проект NumFOCUS, некоммерческой организации 501 (c) (3) благотворительность в США. NumFOCUS предоставляет Matplotlib с финансовая, юридическая и административная поддержка для обеспечения здоровья и устойчивость проекта. Посетите numfocus.org, чтобы узнать больше Информация.
Пожертвования в Matplotlib находятся в ведении NumFOCUS. Для доноров в Соединенные Штаты, ваш подарок не облагается налогом в пределах, предусмотренных закон.Как и в случае любого пожертвования, вам следует проконсультироваться со своим налоговым консультантом. о вашей конкретной налоговой ситуации.
Пожалуйста, рассмотрите возможность пожертвования проекту Matplotlib через организации NumFOCUS или Технологическому товариществу Джона Хантера.
Лицензия Matplotlib основана на программном обеспечении Python Лицензия Foundation (PSF).
Существует активное сообщество разработчиков и длинный список людей, которые сделали значительный вклад.
 По графикам можно определять характер функциональной зависимости,
определять значения величин. Графики позволяют сравнить результаты, полученные
экспериментально, с теорией. На графиках легко находить максимумы и минимумы,
легко выявлять промахи и т. д.
По графикам можно определять характер функциональной зависимости,
определять значения величин. Графики позволяют сравнить результаты, полученные
экспериментально, с теорией. На графиках легко находить максимумы и минимумы,
легко выявлять промахи и т. д. , следует брать большую густоту
экспериментальных точек. Чтобы не пропустить такие особенности, есть смысл строить график сразу во время эксперимента.
, следует брать большую густоту
экспериментальных точек. Чтобы не пропустить такие особенности, есть смысл строить график сразу во время эксперимента.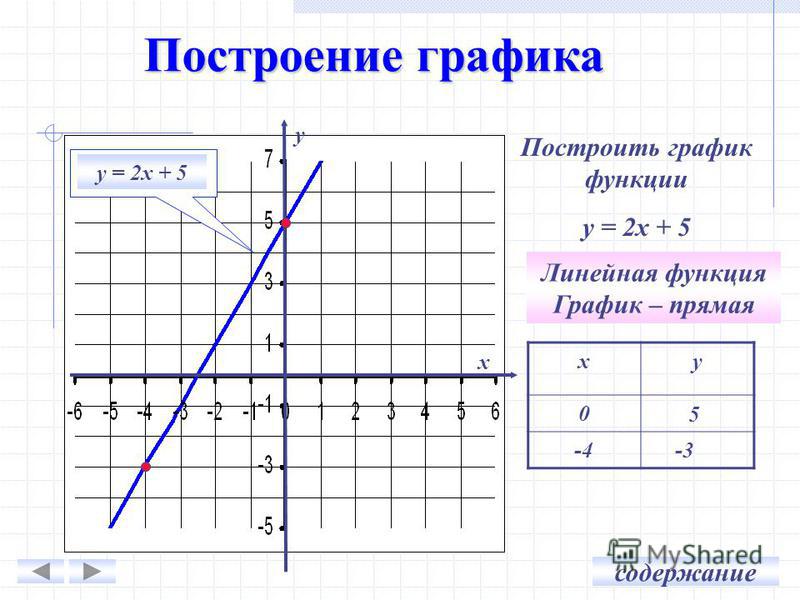

 2 Справочное руководство: 2D-графика
2 Справочное руководство: 2D-графика

 Затем присоединяйтесь к точкам
с линейкой, чтобы получить прямолинейный график.
Затем присоединяйтесь к точкам
с линейкой, чтобы получить прямолинейный график. matplotlib можно использовать в python
скрипты, оболочка python и ipython (ala MATLAB® или Mathematica®),
серверы веб-приложений и шесть наборов инструментов графического пользовательского интерфейса.
matplotlib можно использовать в python
скрипты, оболочка python и ipython (ala MATLAB® или Mathematica®),
серверы веб-приложений и шесть наборов инструментов графического пользовательского интерфейса.
Ваш комментарий будет первым