Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.
Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.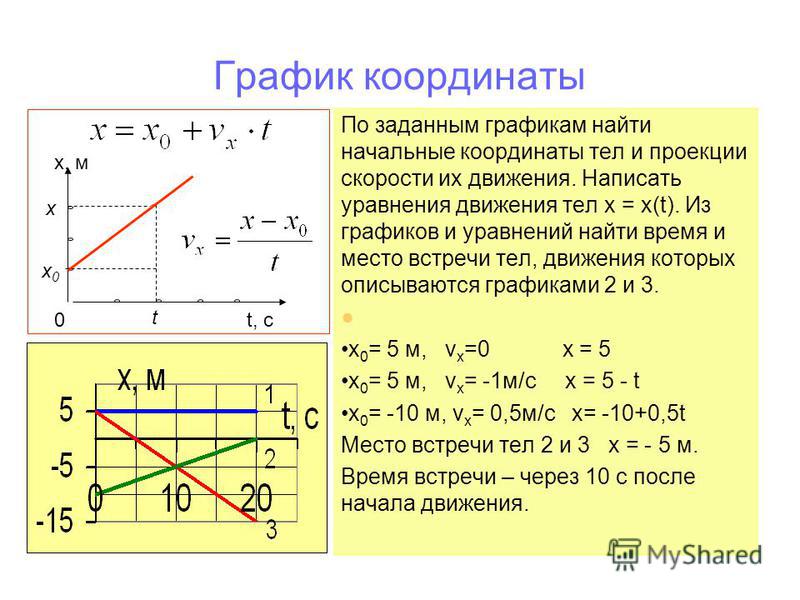
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно .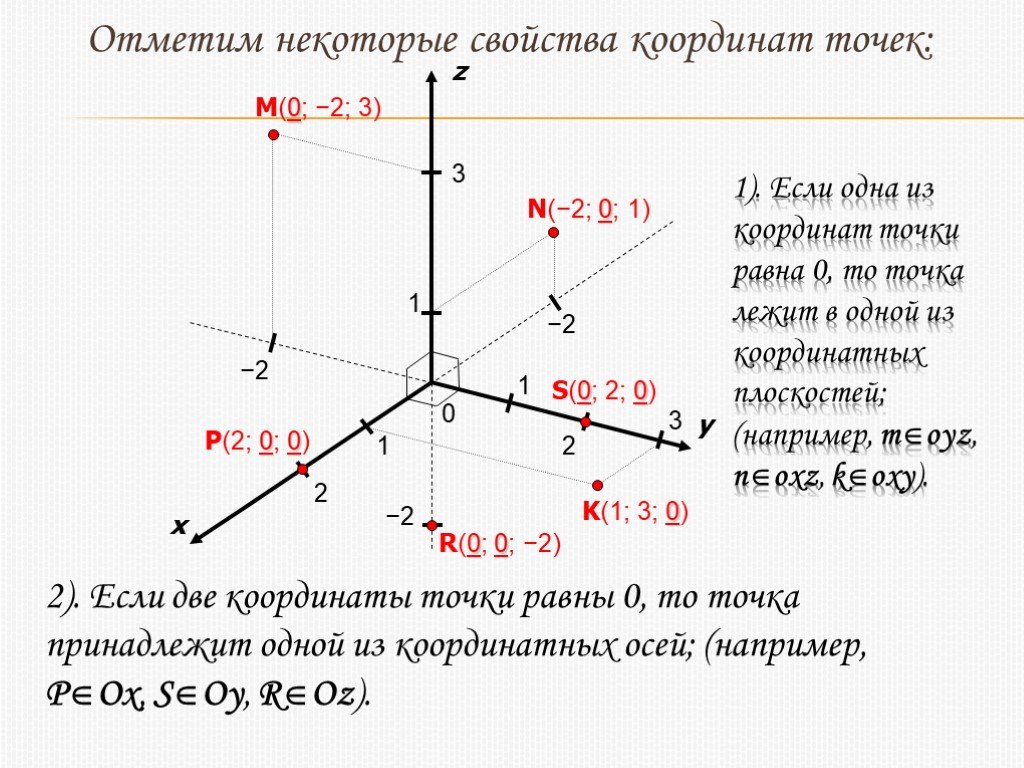 Оно достигается в левом конце отрезка.
Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 08.04.2023
Как в excel построить график с двумя осями x и y
Artman Excel
Допустим, нам надо построить график линейной функции, заданной уравнением
y=2x+7
Для этой функции сделаем таблицу с двумя колонками. В первой колонки будут находится произвольные значения X от 1 до 20, в данном случае шаг у нас единица. Если функция сложная, то шаг лучше взять меньше. Чем меньше шаг, тем точность построения графика выше. Во второй колонки – расчёт значений Y в зависимости от значения x.
В первой колонки будут находится произвольные значения X от 1 до 20, в данном случае шаг у нас единица. Если функция сложная, то шаг лучше взять меньше. Чем меньше шаг, тем точность построения графика выше. Во второй колонки – расчёт значений Y в зависимости от значения x.
Формула для определения Y первой ячейки C4 в нашем случае будет иметь вид:
=2*B4+7
Для остальных ячеек формула аналогичная. Переходим на вкладку Вставка -> Точечная (можно выбрать точечная с гладкими кривыми и маркерами)
Появится белая прямоугольная область, кликаем на неё правым указателем мыши и из пункта меню выбираем Выбрать данные, появляется окошко Выбора источника данных и выбираем весь диапазон данных в ячейках.
В итоги получается вот такой точечный график.
Чтобы добавить линию, необходимо два раза быстро кликнуть на точку графика. Справа появится окошко Формат ряда данных -> Заливка и границы. Здесь можно настроить наш график, укать тип линии (в нашем случае сплошная), цвет, штрихи и т.д.
Справа появится окошко Формат ряда данных -> Заливка и границы. Здесь можно настроить наш график, укать тип линии (в нашем случае сплошная), цвет, штрихи и т.д.
Таблица исходных данных для построения линейной функции в Excel.
| x | y=2x+7 |
| 1 | 9 |
| 2 | 11 |
| 3 | 13 |
| 4 | 15 |
| 5 | 17 |
| 6 | 19 |
| 7 | 21 |
| 8 | 23 |
| 9 | 25 |
| 10 | 27 |
| 11 | 29 |
| 12 | 31 |
| 13 | 33 |
| 14 | 35 |
| 15 | 37 |
| 16 | 39 |
| 17 | 41 |
| 18 | 43 |
| 19 | 45 |
| 20 | 47 |
Пример построение графика для разного шага по оси Х.
Возьмём данные для первого столбца c разным шагом (ось X — первый столбец)
Далее в Excell переходим на вкладку Вставка -> Точечная с прямыми отрезками и маркерами
Далее появляется график, правой клавишей мыши нажимаем на него и в меню выбираем Выбрать данные
Далее выбираем Диапазон данных для диаграммы и жмём Ок
=Лист1!$A$2:$B$8
Получаем график c разным шагом в Excel.
34496
Нанесение точек на координатную плоскость
Результаты обучения
- Определение компонентов декартовой системы координат.
- Точки графика в декартовой координатной плоскости.
Старая история описывает, как философ и математик семнадцатого века Рене Декарт изобрел систему, которая стала основой алгебры, будучи больным в постели. Согласно рассказу, Декарт смотрел на муху, ползущую по потолку, когда понял, что может описать положение мухи по отношению к перпендикулярным линиям, образованным соседними стенами его комнаты. Он рассматривал перпендикулярные линии как горизонтальную и вертикальную оси. Далее, разделив каждую ось на равные единицы длины, Декарт увидел, что можно определить местонахождение любого объекта в двумерной плоскости, используя всего два числа — смещение от горизонтальной оси и смещение от вертикальной оси.
Он рассматривал перпендикулярные линии как горизонтальную и вертикальную оси. Далее, разделив каждую ось на равные единицы длины, Декарт увидел, что можно определить местонахождение любого объекта в двумерной плоскости, используя всего два числа — смещение от горизонтальной оси и смещение от вертикальной оси.
Хотя есть свидетельства того, что идеи, подобные системе сетки Декарта, существовали веками ранее, именно Декарт ввел компоненты, составляющие декартову систему координат , систему сетки с перпендикулярными осями. Декарт назвал горизонтальную ось x- осью , а вертикальную ось y- осью .
Декартова система координат, также называемая прямоугольной системой координат, основана на двухмерной плоскости, состоящей из x — ось и y — ось. Перпендикулярные друг другу оси делят плоскость на четыре части. Каждая секция называется квадрантом ; квадранты нумеруются против часовой стрелки, как показано на рисунке ниже.
Декартова система координат с маркировкой всех четырех квадрантов.
Попробуйте
Центр плоскости — это точка пересечения двух осей. Он известен как исходная точка или точка [латекс]\влево(0,0\вправо)[/латекс]. От начала координат каждая ось далее делится на равные единицы: возрастающие положительные числа справа на x-ось и вверх по оси y-; убывающие отрицательные числа влево по оси x- и вниз по оси y-. Оси простираются до положительной и отрицательной бесконечности, как показано стрелками на рисунке ниже.
Каждая точка на плоскости идентифицируется по координате x- или смещению по горизонтали от начала координат и по координате y- или смещению по вертикали от начала координат. Вместе мы пишем их как заказал пару , указывающую комбинированное расстояние от начала координат в виде [латекс]\влево(х,у\вправо)[/латекс]. Упорядоченная пара также называется парой координат, поскольку она состоит из координат x и y . Например, мы можем представить точку [латекс]\влево(3,-1\вправо)[/латекс] на плоскости, переместив ее на три единицы вправо от начала координат в горизонтальном направлении и на одну единицу вниз в вертикальном направлении. .
Упорядоченная пара также называется парой координат, поскольку она состоит из координат x и y . Например, мы можем представить точку [латекс]\влево(3,-1\вправо)[/латекс] на плоскости, переместив ее на три единицы вправо от начала координат в горизонтальном направлении и на одну единицу вниз в вертикальном направлении. .
Иллюстрация построения точки (3,-1).
При разделении осей на равные интервалы, обратите внимание, что ось x- может рассматриваться отдельно от оси y-. Другими словами, в то время как ось x- может быть разделена и помечена в соответствии с последовательными целыми числами, ось y- может быть разделена и помечена с шагом 2, 10 или 100. Фактически, оси могут представлять другие единицы измерения. например, количество лет по отношению к остатку на сберегательном счете или количество по отношению к стоимости. Рассмотрим прямоугольную систему координат в первую очередь как метод отображения связи между двумя величинами.
A Общее примечание: Декартова система координат
Двумерная плоскость, где ось
- x является горизонтальной осью
- y -ось вертикальная ось
Точка на плоскости определяется как упорядоченная пара [латекс]\влево(х,у\вправо)[/латекс], такая, что x определяется ее горизонтальным расстоянием от начала координат, а y — определяется его вертикальным расстоянием от начала координат.
Пример: построение точек в прямоугольной системе координат
Нанесите точки [латекс]\влево(-2,4\вправо)[/латекс], [латекс]\влево(3,3\вправо)[/латекс] и [латекс]\влево(0,- 3\right)[/latex] в координатной плоскости.
Показать раствор
Попробуйте
Ключевые выводы
Вы можете использовать онлайн-инструмент для построения графиков, чтобы попрактиковаться в построении точек на декартовой плоскости координат. Посмотрите следующее короткое видео, чтобы узнать, как это сделать!
youtube.com/embed/eS6kabG2omI?feature=oembed» frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»»>Теперь попробуйте нанести на график следующие точки с помощью графического онлайн-инструмента.
[латекс](4,0)[/латекс]
[латекс](-1,5)[/латекс]
[латекс](0,-10)[/латекс]
[латекс](2,7)[/латекс]
[латекс]( 3,-5)[/latex]
[latex](-4,-7)[/latex]
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
10 действий на плоскости координат для экономии времени на планирование
«Класс, что вы знаете о построении графиков положительных и отрицательных целых чисел на плоскости координат?» Возможно, это не лучший способ представить эту тему классу, полному шестиклассников. С этой темой ваши ученики будут изучать новый словарный запас и математические понятия, но я думаю, что они также получат массу удовольствия, используя все четыре квадранта координатной плоскости.
Отображение точек координат в первом квадранте входит в курс математики 5-го класса, но в связи с COVID-19 есть вероятность, что у ваших учеников нет никаких предварительных знаний. Даже если ваши ученики не знают, что такое упорядоченная пара, все они могут стать мастерами в этом году!
Мне очень нравится преподавать построение графиков на координатной плоскости, особенно когда используются все четыре квадранта! В Интернете так много фантастических ресурсов, и у нас есть список из 10 отличных вариантов, которые вы можете изучить сегодня!
Занятия :
- Идентификация точки Цифровая квест-комната
- Графическое изображение точки Цифровая квест-комната
- Координатная плоскость Карточки задач
- Координатные точки Лабиринт #1
- Графические точки для поиска сокровищ #1
- Zoo to You: рабочий лист координат
- Nearpod: координатная плоскость
- Нанесение точек на координатную сетку: 4 квадранта
- Запаситесь полками
Не волнуйтесь, если вы новичок в цифровых квестах, их очень легко настроить и объяснить учащимся. Эта квест-комната — отличный способ помочь повторить предыдущие знания и убедиться, что ваши ученики понимают, как определить точку. Первая задача состоит в том, чтобы дать заказанную пару для шести определенных букв. Затем учащиеся должны заполнить пропуск, используя правильное словарное слово. Наконец, учащиеся записывают значение x или y для шести точек и располагают их в порядке от наименьшего к наибольшему.
Эта квест-комната — отличный способ помочь повторить предыдущие знания и убедиться, что ваши ученики понимают, как определить точку. Первая задача состоит в том, чтобы дать заказанную пару для шести определенных букв. Затем учащиеся должны заполнить пропуск, используя правильное словарное слово. Наконец, учащиеся записывают значение x или y для шести точек и располагают их в порядке от наименьшего к наибольшему.
Учитывая, насколько сумасшедшим был прошлый учебный год, я бы порекомендовал пройтись по лексике и отметить точки в первом квадранте. Затем вы можете использовать эту квест-комнату, чтобы бросить вызов своим ученикам, чтобы увидеть, смогут ли они узнать, как строить планы, используя все четыре квадранта. Это делает отличную партнерскую деятельность и действительно заставляет студентов говорить. Мне всегда нравится группировать своих учеников и быть доступным для любых пар, которым может понадобиться дополнительная поддержка.
Удивительно, есть ДВА квеста, которые вы можете использовать с этими стандартами! Цифровая квест-комната Graphing a Point — это именно то, на что это похоже: студенты рисуют точки. Студенты должны определить упорядоченную пару для символа на координатной плоскости. Затем они сопоставляют заказанную пару с буквой, отмеченной на плоскости. Чтобы найти последний фрагмент головоломки, учащиеся перемещают точки на сетку и используют прямую линию, чтобы расположить их по порядку.
Студенты должны определить упорядоченную пару для символа на координатной плоскости. Затем они сопоставляют заказанную пару с буквой, отмеченной на плоскости. Чтобы найти последний фрагмент головоломки, учащиеся перемещают точки на сетку и используют прямую линию, чтобы расположить их по порядку.
Мне нравится использовать эту квест-комнату в качестве обзора перед тестом или быстрой формирующей оценки. Вы легко увидите, понимают ли ученики, как построить заданную точку. Преимущество всех четырех квадрантов в том, что очень легко определить, где студент делает ошибку.
Вы уже пробовали цифровой математический квест? Учителя и ученики в восторге от них! Чтобы узнать, о чем идет речь, нажмите на ссылку ниже, оставьте свой адрес электронной почты, и мы вышлем вам БЕСПЛАТНУЮ цифровую математическую квест-комнату!
Этот квест построен в Google Slides и имеет 3 головоломки: одну для комбинирования одинаковых терминов, одну для распределения свойств и последнюю для решения двухшаговых уравнений. Хватай сегодня!
Хватай сегодня!
ДА! Пришлите мне БЕСПЛАТНУЮ математическую квест-комнату!
Карточки заданий всегда полезны, но этот набор мне нравится больше, чем обычно. Создание собственной активности с координатной плоскостью может занять много времени и усилий. В этих карточках с заданиями на координатную плоскость есть множество вопросов, и все ответы на них предоставлены, что всегда является победой в моей книге.
В этом наборе карточек вы найдете: словарные вопросы, определение точек, определение квадрантов и запись координатных точек. Всего 24 карточки с заданиями и лист ответов ученика. Я сразу вижу в этом отличное занятие для обзора SCOOT перед тестом. Если вы хотите что-то изменить, вы можете вытаскивать пару карточек каждый день для быстрой викторины или работы со звонком.
Это еще один пример отличного ресурса, который сэкономит вам столько времени и усилий! В нашем лабиринте координатных точек есть три отдельных лабиринта, в которых ваши ученики могут практиковаться. К каждому лабиринту прилагается ключ для ответа, который можно использовать в цифровом виде или распечатать.
К каждому лабиринту прилагается ключ для ответа, который можно использовать в цифровом виде или распечатать.
В каждом лабиринте есть вопросы о конкретных координатных плоскостях, которые указаны на бумаге. Студенты доберутся до финиша, правильно определяя координаты и упорядоченные пары. В первом лабиринте задаются вопросы о первом и третьем квадранте, что означает, что одна ось Y отрицательна. Второй лабиринт показывает второй и четвертый квадранты, что означает, что обе оси X отрицательны, а одна ось Y. Последний лабиринт показывает координатную плоскость со всеми четырьмя квадрантами вместе.
Есть множество способов использовать это задание в классе. Мне нравится использовать первые два лабиринта для студентов, которые не готовы отвечать на вопросы обо всех четырех квадрантах сразу. Я могу работать со студентами в небольших группах и помогать им разбираться в самолетах. Я бы отдал последний лабиринт ученикам, которые усвоили концепцию и готовы к испытаниям.
What’s the Point — это задание, которое было разработано для ознакомления с построением координатных точек на графике. Всегда полезно иметь «я делаю, мы делаем» во время занятий по математике, и это позволяет именно это. Есть три разных координатных плоскости с крышками от бутылок с буквами. Студенты должны идентифицировать букву в правильной упорядоченной паре.
Всегда полезно иметь «я делаю, мы делаем» во время занятий по математике, и это позволяет именно это. Есть три разных координатных плоскости с крышками от бутылок с буквами. Студенты должны идентифицировать букву в правильной упорядоченной паре.
Вы можете сделать это на проекторе, а учащиеся будут отвечать на листе бумаги или на белой доске. Это также отличный способ разбудить умы учащихся в качестве звонка или может быть быстрым выходным билетом. Кроме того, они представлены в цифровой версии в Google Slides 9.0199 ТМ . Есть два отдельных занятия, которые предоставляют вам больше возможностей помочь учащимся освоить координатные точки.
Одна из основных причин, по которой я люблю преподавать координатные плоскости, заключается в том, что существует так много доступных игр с зарытыми сокровищами! Эта онлайн-игра на сайте education.com — увлекательный способ для учащихся попрактиковаться в определении точек на координатной плоскости. На острове есть несколько разных ориентиров, и они должны правильно писать точки x и y.
Эта игра будет отличным вариантом для тех, кто рано финиширует. Студенты по-прежнему будут практиковать важные навыки, которые им необходимо знать, но они будут использовать другую среду. Программа также хороша тем, что ученики продолжают попытки, если они вводят неправильную координату.
Этот рабочий лист очень похож на игру с сокровищами, которую я только что упомянул, но это отличный вариант, если вы не можете использовать технологии в своем классе каждый день. На координатной сетке есть 12 изображений, и учащиеся должны определить точки, а также квадранты, в которых они находятся.
Вы можете легко использовать это как средство досрочного завершения, домашнее задание или попросить весь класс работать над ним вместе на доске. В рабочем листе есть отличные вопросы, на которые учащиеся должны ответить, чтобы увидеть свое понимание координатной плоскости. Дополнительное задание, которое вы можете выполнить, — это предложить учащимся написать вопрос, на который должен ответить партнер или весь класс. Бросьте им вызов, чтобы поставить в тупик класс или даже учителя!
Бросьте им вызов, чтобы поставить в тупик класс или даже учителя!
Это видео Nearpod — фантастическое введение в координатную плоскость. Вы можете показать видео своему классу, как и любой клип на YouTube. Он также имеет «интерактивный режим», в котором видео автоматически останавливается и задает вопрос. Вы можете позволить учащимся войти в Nearpod для ответа или использовать другие средства для ответов учащихся.
Мне нравится идея показать это видео в первый день работы с координатными плоскостями, а затем использовать упражнение «В чем суть» для практики. В ролике задаются вопросы «Как много вы уже знаете о координатной плоскости: много, мало или совсем ничего?» и «Где вы могли бы увидеть координатную плоскость в реальной жизни?» Вы можете попросить учащихся ответить на эти вопросы еще раз в качестве выходного билета в конце урока. Или предложите им задать своим сверстникам вопрос о координатной плоскости, на который они знают ответ.
Видео мистера Джея всегда пользуются успехом в моем классе, потому что он так хорошо объясняет с помощью анимации. Этот клип длится почти шесть минут, но он отлично справляется с созданием лесов и показывает, как строить точки. Есть несколько способов использовать это видео, поэтому я дам вам несколько простых идей.
Этот клип длится почти шесть минут, но он отлично справляется с созданием лесов и показывает, как строить точки. Есть несколько способов использовать это видео, поэтому я дам вам несколько простых идей.
Предложите учащимся делать заметки во время просмотра видео. Распечатайте координатную плоскость, похожую на ту, что у г-на J на экране. Когда ваш класс будет смотреть видео, попросите их аннотировать свой график, как это делает он. Это даст вашим ученикам лист для заметок, к которому они могут вернуться, который они помогли создать.
Другой вариант — учащиеся отвечают на вопросы во время просмотра видео, чтобы привлечь внимание всех.
- В каком направлении идет ось Y?
- Опишите происхождение.
- Как прочитать упорядоченную пару?
- Опишите, как нанести (-9,8) на координатную плоскость.
- Что нового вы узнали из этого видео?
Я бы порекомендовал распечатать их, чтобы учащиеся могли ответить или заранее записать их на доске.
Ваш комментарий будет первым