Внеклассный урок — Построение графика квадратичной функции
Построение графика квадратичной функцииВозьмем формулу квадратичной функции y = ax2 + bx + c. Проведя вычисления, можно прийти к другому виду этой формулы (можете вычислить сами):
b b2 – 4ac
y = a(x + — )2 – ————.
2a 4a
Заменим полученные дроби буквами m и n. Тогда мы получим формулу, которая уже известна нам из предыдущего раздела:
y = a(x – m)2 + n, где
b
m = – ——,
2a
b2 – 4ac
n = – ————
4a
Вывод:
Графиком функции y = ax2 + bx + c является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов — сдвига вдоль оси x вправо или влево, а вдоль оси y – вверх или вниз.
b b2 – 4ac
Вершиной этой параболы является (m; n), где m = – ——, n = – ————.
2a 4a
Три особенности этой параболы:
1) x = m (пояснение: ось симметрии параболы параллельна оси y)
2) y = n (пояснение: y = ax2 + bx + c = a(x – m)2 + n = n)
3) при a > 0 ветви параболы направлены вверх, при a<0 – вниз.
Чтобы построить график квадратичной функции, надо в первую очередь найти координаты вершины параболы.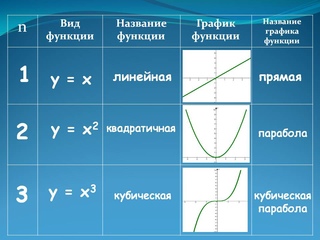
Пример.
Надо построить график функции y = –2x2 + 12x – 19.
Начинаем решать. Для этого отметим, что a = –2, b = 12, c = –19.
Мы видим, что a < 0. Значит, графиком данной функции является парабола, ветви которой направлены вниз.
Найдем координаты ее вершины – то есть значения m и n:
b 12
m = – —— = – ———— = 3
2a 2 · (–2)
Значение n можно вычислить двумя способами. Один из них – формула, приведенная выше. Но поскольку x = m, а y = n (см.выше), то можно найти n более простым способом – непосредственно с помощью нашего выражения –2x2 + 12x – 19, вставляя вместо x значение m, равное 3:
n = –2 · 32 + 12 · 3 – 19 = –1
Итак, вершина параболы имеет координаты (3; –1).
Далее с помощью приведенных формул просто находим координаты еще нескольких точек, отмечаем их на оси координат, соединяем точки – и получаем нашу параболу.
Пошаговое руководство построение графика квадратичной функции
Для того, чтобы начертить график функции в Прямоугольной системе координат, нам необходимы две перпендикулярные прямые xOy (где O это точка пресечения x и y), которые называются «координатными осями», и нужна единица измерения.
У точки в этой системе есть две координаты.
M(x, y): M это название точки, x это абсцисса и она измеряется по Ox, а y это ордината и мерится по Oy.
Две координаты отображают расстояние от точки до двух осей.
Если мы рассмотрим функцию f: A -> B (где A — область определения, B — область значений функции), тогда точку на графике данной функции можно представить в форме P(x, f(x)).
Пример
f:A -> B, f(x) = 3x — 1
If x = 2 => f(2) = 3×2 — 1 = 5 => P(2, 5) ∈ Gf (где Gf это график данной функции).
2-\frac{\Delta}{4a}$
где Δ = b2 — 4ac
Если a > 0, то минимальным значением f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет выпуклая парабола, вершина которой (точка, в которой она меняет направление) это $V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Если a < 0, то минимальное значение f(x) будет $-\frac{\Delta}{4a}$ , которое получается, если $x=-\frac{b}{2a}$. Графиком будет вогнутая парабола, вершина которой это$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
Парабола симметрична относительно прямой, которую она пересекает $x=-\frac{b}{2a}$ и которая называется «осью симметрии».
Именно поэтому, когда мы присваиваем знаячения x, то вибираем их симметричными относительно $-\frac{b}{2a}$.
При построении графика, точки пересечения с осями координат очень важны.
|. Точка, расположенная на оси Ox имеет форму P(x, 0), потому что расстояние от неё до Ox равно 0.
Если точка находиться и на Ox и на графике функции,то она также имеет вид P(x, f(x)) ⇒ f(x) = 0.
Таким образом, для того чтобы найти координаты точки пересечения с осью Ox, мы должны решить уравнение f(x)=0. Мы получаем уравнение a2 + bx + c = 0.
Решение уравнения зависит от знака Δ = b2 — 4ac.
Иммем следующие варианты:
1) Δ < 0,
тогда у уравнения нет решений в R (множестве действительных чисел) и график не пересекает Ox. Форма графика будет:
или
2) Δ = 0,
тогда у уравнения два решения $x_1=x_2=-\frac{b}{2a}$
График касается оси Ox в вершине параболы. Форма графика будет:
или
3) Δ > 0,
тогда у уравнения два разных решения.
$x_1=\frac{-b-\sqrt{\Delta}}{2a}$ и $x_2=\frac{-b+\sqrt{\Delta}}{2a}$
График функции будет пересекать ось Ox в точках M(x1 и Ox.
Форма графика будет:
или
||. Точка, находящаяся на оси Oy имеет форму R(0, y), потому что расстояние от Oy равно 0. Если точка находиться и на Oy и на графике функции, то она также имеет форму R(x, f(x)) ⇒ x = 0 ⇒ R(0, f(0)).
В случае квадратичной функции,
f(0) = a×02 + b×0 + c ⇒ R(0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f(x) = ax2 + bx + c
1. Составляем таблицу переменных, куда заносим некоторые важные значения x.
2. Вычисляем координаты вершины$V(-\frac{b}{2a};-\frac{\Delta}{4a})$.
3. Также записываем 0 в таблицу и нулевые значения симметричные $-\frac{b}{2a}$.
или
4. Мы определяем точку пересечения с осью Ox,решая уравнение f(x)=0 и записываем корни x1 и x2 в таблице.
Δ > 0 ⇒
Δ < 0 ⇒ точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-\frac{b}{2a}$
Δ = 0 ⇒ график касается Ox прямо в вершине параболы. Мы снова выберем два удобных значения, симметричных $-\frac{b}{2a}$. Для лучшего определения формы графика мы может выбрать другие пары значений для x, но они должны быть симметричны $-\frac{b}{2a}$.
5. Мы наносим эти значения на систему координат и строим график, соединяя эти точки.
Пример 1
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=\frac{2}{2}=1$ ⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-\frac{16}{4}=-4$
2. f(0) = -3
Симметричное 0 значение относительно 1 равно 2.
f(2) = -3
Δ = 16 > 0
$x_1=\frac{-b-\sqrt{\Delta}}{2a}=\frac{2-4}{2}=-1$
$x_1=\frac{2+4}{2}=3$
Мы нашли точки:
A(-1; 0)
B(0; -3)
V(1; -4)
C(2; -3)
D(3; 0)
График будет иметь вид:
Пример 2
f: R → R
f(x) = -x2 — 2x + 8
a = -1, b = -2, c = 8
Δ = b2 — 4×a×c = (-2)2 — 4×(-1)×8 = 36
$-\frac{b}{2a}=\frac{2}{-2}=-1$
⇒ V(-1; 9)
1.
$-\frac{\Delta}{4a}=-\frac{-36}{-4}=9$
2. f(0) = 8
3. f(x) = 0 ⇒ -x2 — 2x + 8 = 0
Δ = 36
x1 = 2 и x2 = -4
A(-4; 0)
B(-2; 8)
V(-1; 9)
C(0; 8)
D(2; 0)
Пример 3
f: R → R
f(x) = x2 — 4x + 4
a = 1, b = -4, c = 4
Δ = b2 — 4×a×c = (-4)2 — 4×1×4 = 0
$-\frac{b}{2a}=\frac{4}{2}=2$
⇒ V(2; 0)
1. $-\frac{\Delta}{4a}=0$
2. f(0) = 4
f(4) = 4 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ x2 — 4x + 4 = 0
Δ = 0
x1 = x2 = $-\frac{b}{2a}$ = 2
A(-2; 9)
B(0; 4)
V(2; 0)
C(4; 4)
D(5; 9)
Пример 4
f: R → R
f(x) = -x2 + 4x — 5
a = -1, b = 4, c = -5
Δ = b2 — 4×a×c = 42 — 4×(-1)×(-5) = 16 — 20 = -4
$-\frac{b}{2a}=\frac{-4}{-2}=2$
⇒ V(2; -1)
1.
2. f(0) = -5
f(4) = -5 (симметричное 0 значение относительно 2 равно 4)
3. f(x) = 0 ⇒ -x2 + 4x — 5 = 0,
Δ < 0
У этого уравнения нет решений.
Мы выбрали симметричные значения вокруг 2
A(-1; -10)
B(0; 5)
V(2; -1)
C(4; -5)
D(5; -10)
Если область определения не R (множество действительных чисел), а какой-то интервал, то мы стираем часть графика, которая соответствует тем значениям x, которые не находятся в данном интервале. Необходимо записать конечные точки интервала в таблице.
Пример 5
f: [0; +∞) → R
f(x) = x2 — 2x — 3
a = 1, b = -2, c = -3
Δ = b2 — 4×a×c = (-2)2 — 4×1×(-3) = 16
$-\frac{b}{2a}=1$
⇒ V(1; -4)
1. $-\frac{\Delta}{4a}=-4$
2. f(0) = -3
3. f(x) = 0 ⇒ x2 — 2x — 3 = 0,
Δ = 16
x1 = -1 ∉ [0; ∞)
x2 = 3
A(0; -3)
V(1; -4)
B(2; -3)
C(3; 0)
Квадратичная функция.
2+bx_в+с\)Ось симметрии проходит через вершину параболы и параллельна оси \(y\) (ординат). \(x_1\) и \(x_2\) – нули функции. Их можно найти, приравняв формулу функции к нулю и решив соответствующее квадратное уравнение.
3 параметра позволяющих сопоставить формулу квадратичной функции и график:
|
1. |
\(a>0\) — ветви параболы направлены вверх |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
\(a<0\) — ветви параболы направлены вниз |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2. |
\(c\) равна ординате точки пересечения |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
3. Ответ: Как построить график квадратичной функции (параболу)?Квадратичную функцию можно строить, как и все остальные, выбирая точки наугад (подробнее можно прочитать здесь). Но есть способ позволяющий строить параболу быстрее, выбирая точки осмысленно.
Смотрите также: от чего зависит вид графика функции
Функция вида y = a*x2 + b*x + c, где a, b, c – некоторые вещественные числа, причем График квадратичной функцииИсследуем расположение графика квадратичной функции, в зависимости от формы и вида квадратного трехчлена. Первым критерием, влияющим на общий вид графика квадратичной функции, является знак при старшем коэффициенте. Если при старшем коэффициенте в квадратном трехчлене стоит знак «плюс», то парабола будет иметь ветви направленные вверх. Если при старшем коэффициенте в квадратном трехчлене стоит знак «минус», то парабола будет иметь ветви направленные вниз. Следующим критерием является значение дискриминанта квадратного уравнения. Формула корней квадратного уравнения a*x2 + b*x+ c = 0. x = (-b ± √D)/(2*a), где D = b2 — 4 *a*c. В формуле корней квадратного уравнения выражение D (b2 — 4*a*c) называется дискриминантом квадратного уравнения a*x2 + b*x + c = 0. Такое название пришло из латинского языка, в переводе означает «различитель». В зависимости от того, какое значение имеет дискриминант, квадратное уравнение будет иметь два или один корень либо не иметь корней. Если дискриминант больше нуля, то квадратное уравнение имеет два корня: (x = (-b ± √D)/(2*a)). Если дискриминант равен нулю, то квадратное уравнение имеет один корень: (x = (-b/(2*a)). Корнем квадратного уравнения a*x2 + b*x + c = 0 называют любое значение переменной х, такое, что квадратный трехчлен a*x2 + b*x + c обращается в нуль. Обращение в нуль значение функции равносильно тому, что график функции будет в этой точке пересекать ось Ох. Следовательно, в зависимости от, того какое будет значение дискриминанта, вершина параболы будет расположена относительно оси координат одним из следующих трех способов: ниже оси Ох, на оси Ох, выше оси Ох. На следующем рисунке показаны основные расположения графика квадратичной функции, в зависимости от перечисленных выше двух критериев. Нужна помощь в учебе?Предыдущая тема: Квадратичная функция: ее график и свойства Следующая тема:   Построение графика квадратичной функций: алгоритм и примеры Формула планка для спектра черного телаЯ пытаюсь написать простой код python для графика зависимости интенсивности от длины волны для заданной температуры T=200K. Я не знаю, как определить длину волны (wav) и таким образом получить график Формулы планка. Любая помощь будет оценена по достоинству. python numpy matplotlib scipyПоделиться Источник Unknown 14 марта 2014 в 23:18 2 ответа
Вот основной сюжет. Чтобы построить график с помощью Таким образом, все, что вам нужно сделать, это создать равномерно распределенный массив длин волн ( Затем вычислите интенсивность с помощью вашей функции в каждой из этих точек массива (которая будет храниться в другом И вы видите: Вы, вероятно, захотите очистить метки осей, добавить легенду, построить график интенсивности при нескольких температурах на одном и том же графике, среди прочего. Обратитесь к соответствующей документации matplotlib . Поделиться dr jimbob 14 марта 2014 в 23:33 Поделиться Tobbey 08 июня 2020 в 08:43 Похожие вопросы:Генерировать цветовые палитры спектра Есть ли простой способ конвертировать цветовые модели в Java (RGB, HSV и Lab)? Предполагая, что цветовая модель RGB: Как рассчитать цветовую палитру спектра черного тела? Я хочу использовать его для. Отсутствующий символ шрифта, такой как уменьшенная постоянная Планка Я хочу отобразить два символа Unicode в TextView, но получаю квадраты: — ℏ (уменьшенная постоянная Планка/постоянная Планка более двух ПИ http://www.fileformat.info/info/unicode/char/210f/index.htm… Анализатор спектра с Python? Я хочу создать музыкальный плеер с Python, который использует OpenGL для визуализации звукового спектра. У меня уже есть настроенный движок 3d, и все, что мне нужно, — это получить данные спектра и… Каково значение CieLuv Черного? Страница Википедии о цветовом пространстве CieL*u*v* описывает функцию преобразования из цвета, выраженного в цветовом пространстве XYZ . Для черного цвета, выраженного как (R=0, G=0, B=0) в… Анализатор спектра для .raw 16-битных линейных файлов Мне нужно сделать анализатор спектра для .raw 16-битных линейных файлов. Я посмотрел на это , но это работает только с файлами . Интегрируйте спектр черного тела, чтобы получить болометрическую светимость Солнца Я попытался интегрировать спектр черного тела (функция BBS), чтобы получить болометрическую светимость Солнца (lbol в основном), которая должна составлять около 3.85*10**26 Вт. Но я получаю только… Как получить постоянную Планка в R? Я пытаюсь найти основные константы в статистике R, но не смог этого сделать. На самом деле мне нужна уменьшенная постоянная Планка, но я могу получить ее сам (деление на 2*pi), если смогу получить… Как вы можете интегрировать закон планка, чтобы получить Стефана-Больцмана с помощью python? Я новичок в python и пытаюсь получить закон Стефана Больцмана, интегрируя аналитически закон планка. До сих пор я строил кривые излучения черного тела, но застрял на том, как их интегрировать. Это… Python анализатор спектра Я хочу построить модуль Python, принимающий данные FFT от приемника (полоса пропускания от 20 МГц до 6 ГГц). Сравнение модели с данными для поиска наилучшей подходящей переменной с scipy.optimize.minimize() [python] Мне нужно сравнить модель с данными, чтобы найти наиболее подходящие входные данные. Мои данные-это поверхностное отражение тела (рассеянный свет + тепловое излучение) на разных длинах волн, и я… Таблица математических формулдля ASVABТест ASVAB предназначен для выявления ваших сильных и слабых сторон. Это может помочь вам получить желаемую работу в армии или дать возможность вашей школе дать вам правильный совет по карьере. Есть два раздела ASVAB, которые связаны с математикой: математические знания, которые проверяют ваши навыки алгебры и геометрии, и арифметическое мышление, которое фокусируется на словесных задачах. Поскольку тест ASVAB предназначен для оценки ваших навыков, вам не разрешается использовать какие-либо вспомогательные материалы или калькуляторы при его прохождении. Фракции
процентов
Статистика
Алгебра
Геометрия
Как создать формулу ступенчатой диаграммы в Excel с помощью малой функцииВ нашем последнем пятничном испытании мы изучали пошаговые диаграммы.Если вы его пропустили, вы можете проверить его и загрузить образец файла данных здесь: Friday Step Chart Challenge Кроме того, вы должны проверить самый быстрый ручной способ создания шаговой диаграммы здесь: Как создать пошаговую диаграмму в Excel с помощью 3 быстрых шагов Итак, в этом посте мы исследуем способ создания данных диаграммы с помощью формулы. Мои предпочтительные функции — МАЛЕНЬКИЙ и ВПР. Разбивка 1) Вставить формулы 2) Копируйте, пока не увидите ошибку #Num 3) Создать диаграмму Пошаговая инструкция 1) Вставить формулы Обратите внимание, эта формула была написана, когда ваши данные начинаются, когда Дата находится в ячейке A3 / Год находится в ячейке B3. Если ваши данные находятся в другой ячейке, сначала скопируйте эти формулы в ячейки, описанные ниже, затем скопируйте и вставьте их в желаемое конечное место назначения. Скопируйте формулы, как показано ниже: C3: = МАЛЕНЬКИЙ (Таблица1 [Дата], ОТБР (СТРОКА () / 2,0)) Возвращает наименьшее значение, указанное функцией Trunc (Row () / 2) вашего диапазона данных. Усечение формулы в Excel с последующим делением на 2 поможет вам повторить одно и то же значение в двух последовательных строках. D3: = ЕСЛИ (ЕЧИСЛО (C2), ЕСЛИ (C3 <> C2, D2, ВПР (C3, Таблица1,2, ЛОЖЬ)), ВПР (C3, Таблица1,2, ЛОЖЬ)) Эта формула сначала проверяет, находитесь ли вы в начале набора данных.Если значение в C2 является числом, то мы находимся в середине или конце набора данных, и затем вы попадаете во второй оператор if. Второй оператор if проверяет, находитесь ли вы в первом или втором повторяющемся значении, которое нам нужно для пошаговой диаграммы. Если C3 <> C2, то мы находимся во втором повторяющемся значении, и нам просто нужно вернуть (повторить) значение ячейки D2. Если C3 = C2, мы находимся в первом из двух повторяющихся значений, тогда нам нужно найти значение даты в столбце C. Последний Vlookup смотрит на первый оператор if, и если это не число, то мы нужно найти значение в столбце C. 2) Копируйте, пока не увидите ошибку #Num Так как нам нужна одна точка данных диаграммы для первой и последней точек, а затем нам нужны две точки данных диаграммы для каждой из других точек. Например, в задаче построения графика Prime Rate у нас было всего 341 точка данных. Следовательно, нам нужно скопировать формулу за исходные данные, чтобы получить в общей сложности 680 строк [= (341-2) * 2 + 2]. Если вы скопируете его дальше, вы начнете видеть значение # ЧИСЛО в ячейках, поскольку оно выходит за рамки фактических данных. 3) Создать диаграмму Теперь у вас есть данные шаговой диаграммы. Вам просто нужно выделить ячейки C2: D683, а затем создать линейную диаграмму из меню вставки. У вас будет идеальная пошаговая диаграмма, составленная из VLookUp и Small Functions. Пример файла Вы можете увидеть эти формулы в действии здесь: Step-Chart-Friday-Challenge-Using-Small-Function.xlsx Видео демонстрация Посмотрите, как построить эти формулы пошаговой диаграммы в Excel здесь:  youtube.com/embed/jFDxUwytomU» frameborder=»0″/> Если у вас есть более эффективные формулы для создания шаговой диаграммы, вставьте их в раздел комментариев ниже. Стив = Правда ФОРМУЛА ПРОЧИТАЕМЫХ ГРАФИКОВ ФРАЭдвард Фрай разработал одну из наиболее популярных формул чтения — формулу читаемости графика Фрая .Фрай, который работал стипендиатом программы Фулбрайта в Уганде, также помогал учителям преподавать английский как второй язык (ESL) в течение нескольких лет, начиная с 1963 года. В первые годы своей карьеры Фрай разработал тесты на удобочитаемость, основанные на графике [ Формула удобочитаемости, которая экономит время, , Journal of Reading (1968)]. Этот тест на основе графиков определил удобочитаемость в средней школе; это было подтверждено материалами из первичного и вторичного школ и с результатами других формул читаемости.В 1969 году Фрай расширил график до начальных уровней. В своей книге «Элементарная инструкция по чтению » в 1977 году Фрай расширил график, чтобы проверить его в студенческие годы.  Фрай сообщил, что словарный запас человека продолжает расти в течение учебы в колледже, но способность к чтению варьируется в зависимости от человека и преподаваемых предметов.Фрай стал директором Центра чтения Университета Рутгерса и авторитетом в области того, как люди учатся читать. Формула удобочитаемости графика ФраяШаг 1 : Случайным образом выберите 3 образца отрывков из 100 слов (исключите числа из числа слов). Шаг 2 : Подсчитайте количество предложений во всех трех отрывках из 100 слов, оценив долю последнего предложения с точностью до 1/10. Шаг 3 : Подсчитайте количество слогов во всех трех отрывках из 100 слов. Составьте таблицу следующим образом:
Шаг 4 : Введите график со средней длиной предложения и количеством слогов.  Нанесите точку на пересечении двух линий. Область, в которой нанесена точка, обозначает приблизительный уровень чтения для содержания.Шаг 5 : Если вы обнаружите большую изменчивость, вы можете добавить больше выборок в среднее значение. Щелкните изображение, чтобы увидеть увеличенную версию Fry Graph. Очки, отображаемые в темной области (длинные предложения и длинные слова), недействительны. Формула удобочитаемости графика Фрая и связанный с ней график часто используются для обеспечения консенсуса удобочитаемости в нормативных целях, таких как удобочитаемость, в отрасли здравоохранения, чтобы более широкая часть населения могла понимать публикации и получать к ним доступ с высоким уровнем читаемости. .Детское питание — Американский семейный врач 2. Gartner LM,
Мортон Дж.
Лоуренс Р.А.,
и другие.,
для Секции грудного вскармливания Американской академии педиатрии.
Грудное вскармливание и употребление грудного молока. 3. Обогащение детского питания железом. Американская академия педиатрии. Комитет по питанию. Педиатрия . 1999; 104 (1 п.1): 119–123. 4.Хопкинс Д., Эммет П., Управляйте C, Роджерс I, Благородный S, Эмонд А. Кормление грудных детей в течение вторых 6 месяцев жизни связано со статусом железа: обсервационное исследование. Арч Дис Детский . 2007. 92 (10): 850–854. 5. Симмер К, Патоле СК, Rao SC. Добавки длинноцепочечных полиненасыщенных жирных кислот у доношенных детей. Кокрановская база данных Syst Rev . 2008; (1): CD000376. 6. Симмер К, Шульцке С.М., Патоле С.Добавка длинноцепочечных полиненасыщенных жирных кислот недоношенным детям. Кокрановская база данных Syst Rev . 2008; (1): CD000375. 7. Зал РТ,
Кэрролл RE.
Младенческое вскармливание. 8. Хендерсон Г., Фэйи Т, Макгуайр В. Смесь, обогащенная питательными веществами, по сравнению со стандартной смесью для недоношенных новорожденных после выписки из больницы. Кокрановская база данных Syst Rev . 2007; (4): CD004696. 9. Хейман МБ. Комитет по питанию. Непереносимость лактозы у младенцев, детей и подростков. Педиатрия . 2006. 118 (3): 1279–1286. 10. Американская академия педиатрии. Комитет по питанию. Гипоаллергенные смеси для младенцев. Педиатрия . 2000; 106 (2 п.1): 346–349. 11. Бхатия Дж., Грир Ф, для Комитета по питанию Американской академии педиатрии. Использование смесей на основе соевого белка в кормлении грудных детей. Педиатрия . 2008. 121 (5): 1062–1068. 12. Крейг В. Р.,
Хэнлон-Дирман А,
Синклер C,
Табак S,
Моффатт М. 13. Гарнизон ММ, Кристакис Д.А. Систематический обзор методов лечения детских колик. Педиатрия . 2000; 106 (1 пт 2): 184–190. 14. Отсутствие G, Фокс Д, Нортстоун К, Голдинг Дж, для группы изучения лонгитюдных исследований родителей и детей Avon. Факторы, связанные с развитием аллергии на арахис в детстве. N Engl J Med . 2003. 348 (11): 977–985. 15. Клемола Т, Калимо К, Пусса Т, и другие. Кормление соевой смесью детей с аллергией на коровье молоко: развитие иммуноглобулиновой Е-опосредованной аллергии на сою и арахис. Pediatr Allergy Immunol . 2005. 16 (8): 641–646. 16. Осборн Д.А.,
Синн Дж.
Формулы, содержащие гидролизованный белок, для профилактики аллергии и пищевой непереносимости у младенцев. 17. Аллен UD, Маклеод К., Ван Э. Коровье молоко в сравнении с смесями на основе сои при легкой и умеренной диарее: рандомизированное контролируемое исследование. Acta Paediatr . 1994. 83 (2): 183–187. 18. Стром БЛ, Шиннар Р, Зиглер Э. и другие. Воздействие смеси на основе сои в младенчестве, а также эндокринологические и репродуктивные результаты в молодом взрослом возрасте. ЯМА . 2001. 286 (7): 807–814. 19. Эссекс К. Фитоэстрогены и детские смеси на основе сои. BMJ . 1996. 313 (7056): 507–508. 20. Зал РТ,
Калленбах JC,
Шихан МБ,
и другие.
Сравнение смеси соевых изолятов, содержащих кальций и фосфор, с молочной смесью для недоношенных детей с преобладанием сыворотки для младенцев с очень низкой массой тела при рождении. 21. Callenbach JC, Шихан МБ, Абрамсон SJ, Зал RT. Этиологические факторы рахита у детей с очень низкой массой тела при рождении. Дж. Педиатр . 1981. 98 (5): 800–805. 22. Sandhu BK, Изолаури Э, Уокер-Смит Дж. А., и другие. Многоцентровое исследование от имени Рабочей группы по острой диарее Европейского общества педиатрической гастроэнтерологии и питания.Раннее вскармливание в детском гастроэнтерите. J Педиатр Гастроэнтерол Нутр . 1997. 24 (5): 522–527. 23. Agostoni C, Fiocchi A, Рива Э, и другие. Рост младенцев с IgE-опосредованной аллергией на коровье молоко, получавших различные смеси в период прикорма. Pediatr Allergy Immunol . 2007. 18 (7): 599–606. 24. Hill DJ,
Марч Ш.,
Рафферти К,
Уоллис П.,
Зеленый CJ. 25. Грир FR, Шихерер Ш., Беркс А.В., для Комитета по питанию Американской академии педиатрии, Секции аллергии и иммунологии Американской академии педиатрии. Влияние раннего диетического вмешательства на развитие атопического заболевания у младенцев и детей: роль ограничения питания матери, грудного вскармливания, времени введения прикорма и гидролизованных смесей. Педиатрия . 2008. 121 (1): 183–191. 26. Мукарзель А.А., Абдельнур Х, Акачеян К. Влияние предварительно загущенной смеси на рН пищевода и опорожнение желудка у младенцев с ГЭР. Дж Клин Гастроэнтерол . 2007. 41 (9): 823–829. 27. Lothe L,
Линдберг Т,
Якобссон И.
Смесь коровьего молока как причина детских колик: двойное слепое исследование. 28.Кэмпбелл JP. Диетическое лечение детских колик: двойное слепое исследование. J R Coll Gen Pract . 1989. 39 (318): 11–14. 29. Lucassen PL, Ассендельфт WJ, Габбельс Дж. У., ван Эйк Дж. Т., ван Гелдроп WJ, Невен АК. Эффективность лечения детской колики: систематический обзор [опубликованные поправки опубликованы в BMJ. 1998, 317 (7152): 171]. BMJ . 1998. 316 (7144): 1563–1569. 30. Таубман Б. Консультирование родителей по сравнению с отказом от коровьего молока или белка соевого молока для лечения синдрома детской колики: рандомизированное исследование. Педиатрия . 1988. 81 (6): 756–761. Что на нем и как его использовать Если вы собираетесь сдавать экзамен по биологии AP, у нас есть хорошие новости! Во время теста AP у вас будет доступ к таблице формул, полной полезных уравнений и определений. Вот где мы вступаем! В этом руководстве мы рассмотрим все, что вам нужно знать о справочном листе AP Bio.Мы объясним каждое уравнение и определение, которое оно включает, покажем вам, как выглядит лист формул, рассмотрим важную информацию, которую он не содержит, но которую вы должны знать, и дадим вам советы о том, как получить от него максимальную пользу. Что находится на листе формул AP Bio?Лист формул AP Biology — это на самом деле две страницы, заполненные формулами и определениями, которые могут помочь вам во время экзамена AP. Таблица формул будет в начале разделов экзамена с множественным выбором и свободным ответом, поэтому у вас будет доступ к нему для всего теста AP.Это означает, что вам не нужно запоминать какую-либо информацию, содержащуюся в таблице формул! Так что же на этом справочном листе AP Bio? Посмотрите здесь, а также на скриншоты ниже (нажмите на каждое изображение, чтобы увеличить). Уравнение AP Biology охватывает шесть основных тем. Ниже изображений мы перечислим, какие уравнения и информацию включает каждая тема в таблицу формул.
Статистический анализ и вероятностьФормулы
Информация
Скорость и ростФормулы
Площадь и объемФормулы
Водный потенциалФормулы
Информация
РазведениеФормулыСвободная энергия ГиббсаФормулыРазноеФормулы
Всего на листе био-формул AP есть 23 формулы. Когда вы смотрите на уравнение, например, для свободной энергии Гиббса, даже если вы знаете (или можете видеть на листе формул), что формула ΔG = ΔH — TΔS, это мало что значит, если вы не знать, что означает каждый символ. Таким образом, помимо формул, таблица уравнений AP Biology также предоставляет информацию, необходимую для более простого использования этих уравнений. Что не указано в листе формул AP Bio, что вам нужно знать для экзамена? Справочный лист AP Biology отлично справляется с описанием формул, которые вам необходимо знать для экзамена, но есть и другая важная информация, относящаяся к формулам, которую вам будет полезно запомнить. Кривые численности населенияНа листе уравнений AP Biology есть несколько уравнений о росте и изменении популяции, но вам также следует знать, как выглядят различные кривые численности населения. Есть два основных вопроса, которые необходимо знать: Экспоненциальный рост (J-кривая) Экспоненциальный рост — это когда темп прироста на душу населения остается неизменным независимо от размера населения, что приводит к тому, что население растет быстрее по мере его увеличения. Это заставляет рост населения принимать форму буквы «J» на графике. В конце концов, этот тип быстрого роста населения будет остановлен ограничивающим фактором окружающей среды, например, нехваткой пищи или места. Логистический рост (S-образная кривая) У популяций, демонстрирующих логистический рост, рост на на душу населения сокращается по мере того, как население приближается к пропускной способности (k) , что является максимально возможным размером населения в окружающей среде. Правила pHВ справочном листе AP Bio есть одна одинокая формула pH, но pH — важная тема, и есть несколько других формул и правил, связанных с ней, которые вы должны знать. Вот три полезных формулы pH: Для преобразования между [H + ] и pH: pH = -log [H + ] (это уравнение включено в таблицу формул) Для преобразования между [OH — ] и pOH: pOH = -log [OH — ] Для любого водного раствора при 25 ∘ C: pH + pOH = 14 Маловероятно, что вам действительно нужно будет проводить расчеты с использованием этих формул, но их важно знать, чтобы вы могли понять, как pH, pOH, [H + ] и [OH — ] связаны с каждым из них. Другой.Например, посмотрев на первое уравнение выше и введя несколько номеров образцов, вы увидите, что по мере уменьшения [H +] pH повышается, а по мере увеличения [H + ] pH понижается. Вас также могут спросить, является ли раствор кислотным, основным или нейтральным. Вот правила для этого:
Советы по максимально эффективному использованию AP Bio Formula SheetКак видите, таблица с уравнениями AP Biology может быть очень полезна во время экзамена, поскольку экономит время на запоминание примерно двух десятков уравнений.В этом разделе мы обсудим три совета, которые помогут вам извлечь из этого максимальную пользу. # 1: Просмотрите, но не запоминайте Некоторые студенты думают, что, поскольку в день экзамена у них будет с собой лист с формулами AP Bio, им не нужно заранее об этом беспокоиться. Тем не менее, вы не хотите тратить драгоценное время во время экзамена AP на поиск формул и попытки выяснить, какая из них будет для вас наиболее полезной. # 2: Умейте использовать каждую формулуСправочный лист AP Bio содержит 23 формулы, и вы должны знать, как работает каждая из них, до дня тестирования. Совет колледжа не предназначен для включения посторонней информации в листы с формулами, поэтому , если формула включена в лист, означает, что есть большая вероятность, что вам нужно будет использовать ее на экзамене. Даже если вы не будете использовать все формулы в день тестирования, вы должны знать, как все они работают. Вы не хотите тратить свой экзамен, пытаясь научиться использовать, скажем, формулу свободной энергии Гиббса, и надеяться, что вы поняли ее правильно! Задолго до дня экзамена обязательно изучите каждую формулу на листе, убедитесь, что вы понимаете ее и знаете, как ее использовать. # 3: Пройдите практические тесты с формулойОтветы на практические вопросы и прохождение практических тестов с использованием таблицы формул AP Bio также являются ключом к успешной сдаче экзамена.Перед экзаменом вам следует пройти несколько практических тестов AP Biology, и для каждого из них вы должны использовать официальный лист формул. Ваш учитель, вероятно, также даст вам копию листа формул для ваших экзаменов в классе, чтобы вы тоже могли попрактиковаться. Если вам нужна помощь в поиске практических тестов, ознакомьтесь с нашим руководством, в частности, где найти лучшие практические вопросы и тесты AP Biology. Что дальше? Является ли биология AP особенно сложной по сравнению с другими AP? Прочтите эту статью, чтобы подробно обсудить уровень сложности курса и экзамена. Хотите получить больше рекомендаций по подготовке к экзамену AP по биологии? Мы создали для вас лучшее учебное пособие по AP-биологии, в котором есть все необходимое для успешного прохождения теста. Желаете сразу начать работу с AP Bio Pre? Мы рассматриваем клеточную теорию, ферменты, клеточные структуры (эндоплазматический ретикулум и клеточную мембрану), гомологичные и аналогичные структуры, а также уравнение фотосинтеза с помощью специальных руководств. Хотите улучшить свой результат SAT на 160 баллов или ваш результат ACT на 4 балла? Мы написали руководство для каждого теста о 5 лучших стратегиях, которые вы должны использовать, чтобы улучшить свой результат.Скачайте бесплатно сейчас: Калькулятор ИМТРезультатИМТ = 20,1 кг / м 2 ( Нормальный )
Калькулятор индекса массы тела (ИМТ) может использоваться для расчета значения ИМТ и соответствующего статуса веса с учетом возраста. BMI введение ИМТ — это показатель худощавости или полноты человека, основанный на его росте и весе, и предназначен для количественной оценки массы ткани. Он широко используется в качестве общего индикатора того, соответствует ли человек своему росту.В частности, значение, полученное при вычислении ИМТ, используется для классификации того, имеет ли человек недостаточный вес, нормальный вес, избыточный вес или ожирение, в зависимости от того, в какой диапазон попадает это значение. Эти диапазоны ИМТ варьируются в зависимости от таких факторов, как регион и возраст, и иногда делятся на подкатегории, такие как сильно пониженный вес или очень тяжелое ожирение. Избыточный или недостаточный вес может иметь значительные последствия для здоровья, поэтому, хотя ИМТ является несовершенным показателем здоровой массы тела, он является полезным индикатором того, требуются ли какие-либо дополнительные тесты или действия. Таблица ИМТ для взрослыхЭто рекомендованная Всемирной организацией здравоохранения (ВОЗ) масса тела на основе значений ИМТ для взрослых. Применяется как для мужчин, так и для женщин от 18 лет и старше.
График ИМТ для взрослых Это график категорий ИМТ на основе данных Всемирной организации здравоохранения. Таблица ИМТ для детей и подростков 2-20 летЦентры по контролю и профилактике заболеваний (CDC) рекомендуют категоризацию ИМТ для детей и подростков в возрасте от 2 до 20 лет.
Таблица ИМТ для детей и подростков в возрасте 2-20 летЦентры по контролю и профилактике заболеваний (CDC) График роста процентилей ИМТ к возрасту. Таблица для мальчиковТаблица для девочек Риски, связанные с лишним весомИзбыточный вес увеличивает риск ряда серьезных заболеваний и состояний здоровья. Ниже приведен список указанных рисков по данным Центров по контролю и профилактике заболеваний (CDC):
Как видно из приведенного выше списка, избыточный вес может привести к многочисленным отрицательным, в некоторых случаях летальным исходам. Риски, связанные с недостаточным весомНедостаточный вес имеет свои риски, перечисленные ниже:
В некоторых случаях недостаточный вес может быть признаком какого-либо основного состояния или заболевания, например нервной анорексии, которое имеет свои риски. Ограничения ИМТХотя ИМТ является широко используемым и полезным индикатором здоровой массы тела, у него есть свои ограничения. ИМТ — это всего лишь оценка, которая не может принимать во внимание состав тела. Из-за большого разнообразия типов телосложения, а также распределения мышечной, костной массы и жира, ИМТ следует рассматривать вместе с другими измерениями, а не использовать в качестве единственного метода для определения здоровой массы тела человека. Для взрослых: ИМТ не может быть полностью точным, потому что это показатель избыточной массы тела, а не избыточного жира.На ИМТ также влияют такие факторы, как возраст, пол, этническая принадлежность, мышечная масса и жировые отложения, а также уровень активности, среди прочих. Например, пожилой человек, имеющий нормальный вес, но совершенно неактивный в повседневной жизни, может иметь значительное количество лишнего жира, даже если он не тяжелый.
У детей и подростков: Те же факторы, которые ограничивают эффективность ИМТ для взрослых, могут также применяться к детям и подросткам.Кроме того, рост и уровень полового созревания могут влиять на ИМТ и жировые отложения у детей. ИМТ является лучшим индикатором избыточного жира у детей с ожирением, чем у детей с избыточным весом, у которых ИМТ может быть результатом повышенного уровня либо жировой, либо обезжиренной массы (всех компонентов тела, кроме жира, который включает воду, органы и т. При этом ИМТ является довольно показательным показателем телесного жира для 90-95% населения и может эффективно использоваться вместе с другими показателями для определения здоровой массы тела человека. Формула ИМТНиже приведены уравнения, используемые для расчета ИМТ в Международной системе единиц (SI) и обычной системе США (USC) на примере человека весом 5’10 дюймов и 160 фунтов:
Ponderal Index Ponderal Index (PI) похож на BMI в том, что он измеряет худобу или полноту человека в зависимости от его роста и веса. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2+5x+1\) \(x_в= \frac{-5}{2}=-2,5\) так же как на графике 3
2-4x+5=0\) нет корней, т.к. нету \(x\) при которых y будет равен нулю (функция не пересекает ось \(x\))
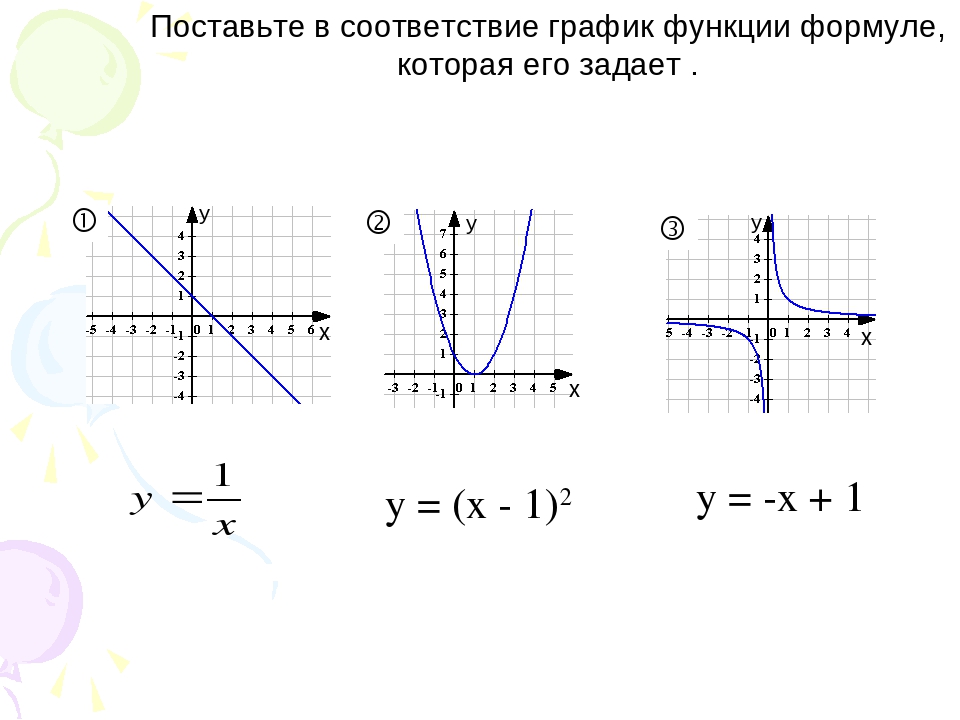Если дискриминант отрицателен, то квадратное уравнение не имеет корней.
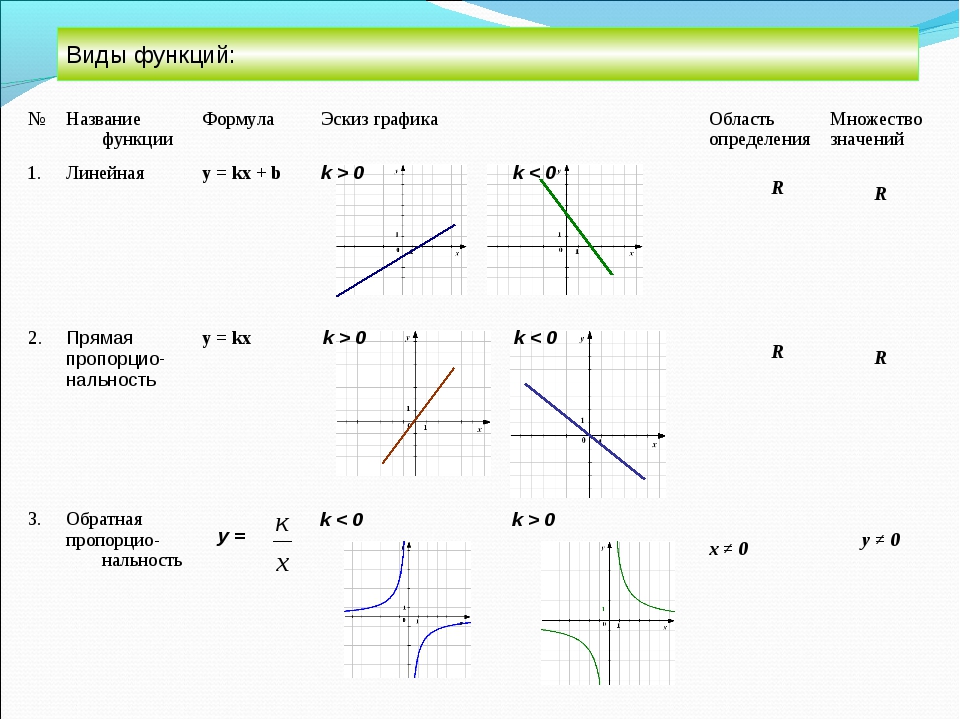Пока что у меня есть вот это…
..
)
plt.hold(True) # doesn't erase plots on subsequent calls of plt.plot()
plt.plot(wavelengths*1e9, intensity4000, 'r-')
# plot intensity4000 versus wavelength in nm as a red line
plt.plot(wavelengths*1e9, intensity5000, 'g-') # 5000K green line
plt.plot(wavelengths*1e9, intensity6000, 'b-') # 6000K blue line
plt.plot(wavelengths*1e9, intensity7000, 'k-') # 7000K black line
# show the plot
plt.show()
..
wav. Знаете ли вы какой-нибудь учебник/пример, который может помочь…
Моя цель такова: Оцените уровень шума. Обнаружение энергии над уровнем шума (обнаружение…
Чтобы показать, что вы на самом деле знаете , и могут делать , вам нужно хорошо подготовиться. Следующая таблица формул может помочь в этой подготовке. В нем перечислены основные формулы, которые вам понадобятся, если вы хотите улучшить свой результат в разделах ASVAB Math. Попробуйте использовать его, чтобы пройти образцы тестов, которые есть у нас в Union Test Prep!
б) = b \ cdot \ log (a) \)
Проверьте это в пошаговом руководстве, видеоуроке и бесплатном образце файла ниже.
Посмотрите видео ниже, чтобы понять, что я имею в виду.
Педиатрия .
2005. 115 (2): 496–506.
Педиатр Ред. .
2000. 21 (6): 191–199.
Метоклопрамид, утолщенные кормления и позиционирование при гастроэзофагеальном рефлюксе у детей до двух лет. Кокрановская база данных Syst Rev .
2004; (4): CD003502.
Кокрановская база данных Syst Rev .
2006; (4): CD003664.
J Педиатр Гастроэнтерол Нутр .
1984. 3 (4): 571–576.
Эффективность смесей на основе аминокислот в облегчении симптомов аллергии на коровье молоко: систематический обзор. Clin Exp Allergy .
2007. 37 (6): 808–822.
Педиатрия .
1982; 70 (1): 7–10.
Однако вам нужно хорошо понимать, что находится на листе формул AP Bio и как его использовать, чтобы он был полезен вам во время теста.
Однако, как вы можете видеть, взглянув на таблицу формул, она содержит гораздо больше информации, чем просто 23 формулы. Это потому, что лист формул включает несколько ключей, которые идентифицируют различные символы, используемые в формулах. Это чрезвычайно полезная информация, поскольку она дает больше контекста для формул. Например, хотя раздел о потенциале воды в таблице формул содержит только две формулы, в нем есть ключевые поясняющие символы для потенциала давления, потенциала раствора, константы ионизации, молярной концентрации, константы давления и температуры в Кельвинах.
Население выравнивается, как только оно достигает своей вместимости, из-за каких-то ограничений, таких как еда, жилье или пространство.
Это означает, что вам нужно будет просмотреть таблицу формул задолго до теста. Вы должны стремиться иметь общее представление о том, что включено в таблицу формул, а также о том, где находятся различные уравнения. Затем во время экзамена вы можете быстро найти конкретную формулу, которую ищете.
Если вам не удается найти одну или несколько формул, найдите в учебнике, где они обсуждаются, или попросите помощи у учителя.
Используйте вкладку «Метрические единицы» для Международной системы единиц или вкладку «Другие единицы» для преобразования единиц в американские или метрические единицы. Обратите внимание, что калькулятор также вычисляет Ponderal Index в дополнение к BMI, оба из которых подробно обсуждаются ниже.
Обратитесь к таблице ниже, чтобы увидеть различные категории на основе ИМТ, которые используются калькулятором.
Пунктирными линиями обозначены подразделения в рамках основной категоризации.
Как правило, человек должен стараться поддерживать ИМТ ниже 25 кг / м 2 , но в идеале должен проконсультироваться со своим врачом, чтобы определить, нужно ли ему вносить какие-либо изменения в свой образ жизни, чтобы стать более здоровым.
Проконсультируйтесь с врачом, если вы считаете, что у вас или у кого-то из ваших знакомых недостаточный вес, особенно если причина недостаточного веса не кажется очевидной.
Это будет считаться нездоровым, в то время как более молодой человек с более высоким мышечным составом и тем же ИМТ будет считаться здоровым. У спортсменов, особенно бодибилдеров, которых можно было бы считать избыточным весом из-за того, что мышцы тяжелее жира, вполне возможно, что они на самом деле имеют здоровый вес для их состава тела.Как правило, согласно CDC:
мышцы и др.). У худых детей разница в ИМТ также может быть связана с обезжиренной массой.
Ваш комментарий будет первым