Преобразование графика квадратичной функции — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Преобразование
графика квадратичной
функции
Заполни пропуски …
1).Функция у = aх2 + bx + c, где а, b, c – заданные действительные
числа, а 0, х – действительная переменная, называется … функцией.
2).График функции у = ах2 при любом а 0 называют
….
3).Функция у = х2 является … (возрастающей, убывающей) на
промежутке х 0.
4).Значения х, при которых квадратичная функция равна нулю, называют
функции.
5).Точку пересечения параболы с осью симметрии называют …
параболы.
6).При а >0 ветви параболы у = ах2 направлены … .
7).Если а< о и х 0, то функция у = ах2 принимает
… (положительные, отрицательные) значения.
Какие преобразования происходят с
графиком?
1. у=х2
У
2. у=2х2
9
3. у= х2
4
1
-1
1 2 3
Х
Выводы:
График функции у=2х2 можно получить из
параболы у=х2 растяжением вдоль оси
Оу в 2 раза;
График функции у= х2 можно получить из
параболы у=х2 сжатием относительно
оси Оу в 2 раза;
Построить графики функций в одной
системе координат и сделать выводы:
1. у=х2;
2. у=х2+2;
У
3. у=х2-2.
9
4
2
1
-1
-2
1 2 3
Х
Выводы записать:
1. График функции у=х2+2 – парабола,
полученная в результате сдвига вверх на
2единицы вдоль оси Оу графика функции
у=х2;
2.
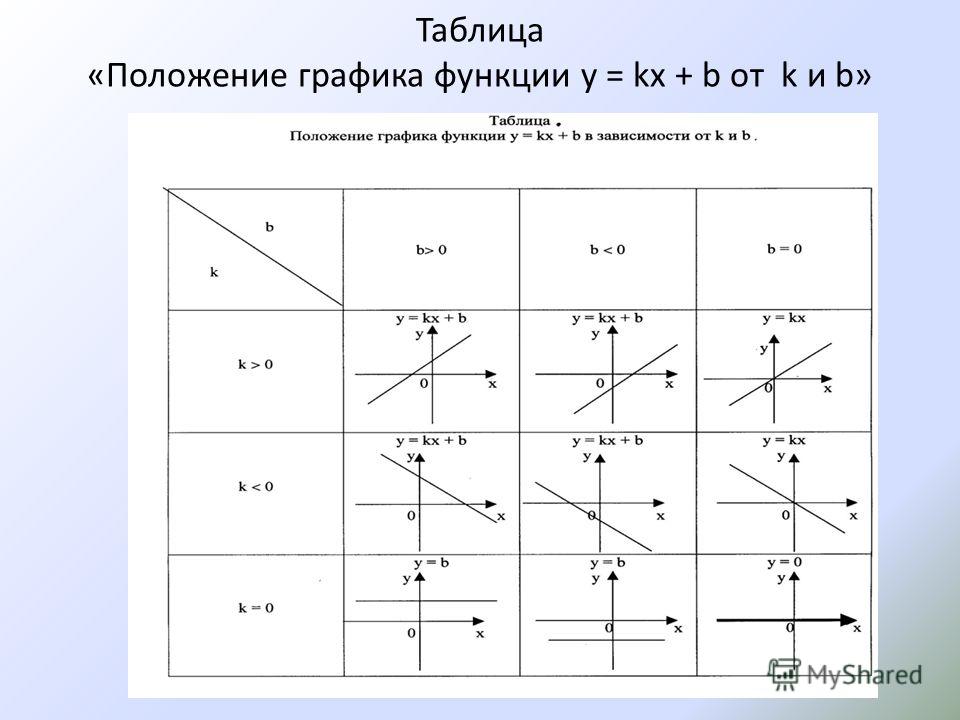 График функции у=х2+2 – парабола,
График функции у=х2+2 – парабола,полученная в результате сдвига вниз на 2
единицы вдоль оси Оу графика функции
у=х2.
Построить графики функций в одной
системе координат и сделать выводы:
1. у=х2;
2.
У
у=(х+1)2;
3. у=(х-1)2.
9
4
1
-1
1 2 3
Х
Выводы записать:
1. График функции у=(х+1)2 – парабола,
полученная в результате сдвига влево на
1 единицу вдоль оси Ох графика
функции у=х2;
2. График функции у=(х-1)2 – парабола,
полученная в результате сдвига вправо
на 1 единицу вдоль оси Ох графика
функции у=х2.
Преобразования графика
квадратичной функции
Преобразования
графика
Симметрия
Растяжение,
сжатие
Сдвиг
Выводы
Функция
Преобразование графика функции у=f(х)
у=-f(х)
Симметрия относительно оси ОХ
у=аf(х)
Растяжение графика вдоль оси ОУ в к раз,
у=f(х)+m
Сдвиг вдоль оси ОУ на m единиц вверх,
если m>0; на ImI единиц вниз, если m<0.
у=f(х-n)
Сдвиг вдоль оси ОХ на а единиц вправо,
если n > 0; на InI единиц влево, если n < 0.
ПРОВЕРЬ СЕБЯ.
График какой функции
рисунке?
изображен
на
12. График какой функции изображенной на рисунках соответствует указанной формуле у=3х2+1
График какой функции изображенной на рисункаху=3х2+1
соответствует указанной формуле
4
1
1
1
1
13. График какой функции изображенной на рисунках соответствует указанной формуле у= -0,5х2-3
3-3
-3
-3
14. График какой функции изображенной на рисунках соответствует указанной формуле
у= -2(х-2)22
-2
2
-2
15. График какой функции изображенной на рисунках соответствует указанной формуле у= (х+2)2 — 4
График какой функции изображенной на рисункаху= (х+2)2 — 4
соответствует указанной формуле
-2
2
-4
-4
2
4
-4
-2
Какой формулой задается график функции изображенной на
рисунке
у = (х+2)2 – 2
у = 2 — (х+2)2
2
-2
у = 2+ (х+2)2
у = (х+2)2
Какой формулой задается график функции изображенной
на рисунке
у = 2 (х+3)2 +4
4
у = 2(х-4)2 — 3
3
у = 3 — 2(х+4)2
у = -2(х-3)2 + 4
English Русский Правила
Функция тангенса: онлайн калькулятор, формулы, график
Функция
{$ main. types[data.type] $}
types[data.type] $}
Введите угол α{$ main.angles[data.angle1] $}
Результат расчёта
{$ data.type $}(α) = {$ result[0]|number:data.round $}
Введите {$ data.type $}(α){$ main.angles[data.angle2] $}
Результаты расчёта
- {$ result[1] $}
- {$ result[2] $}
Округлять до {$ data.round $} {$ Plural(data.round, [‘знака’, ‘знаков’, ‘знаков’]) $} после запятой
Тангенс — тригонометрическая функция, численно равная соотношению длин противолежащего и прилежащего катета. Тангенс широко используется во многих современных приложениях.
История вопроса
Тригонометрия берет свое начало в Древнем Вавилоне, когда ученые изучали свойства сторон прямоугольного треугольника. Именно тогда была сформулирована теорема, постулирующая соотношение катетов и гипотенузы, доказанная только через полторы тысячи лет самосским математиком Пифагором. Изначально использовался только синус, который рассчитывался как половина хорды окружности, описанной вокруг прямоугольного треугольника.
Изначально использовался только синус, который рассчитывался как половина хорды окружности, описанной вокруг прямоугольного треугольника.
Тангенс появился гораздо позднее, когда перед учеными возникла задача определения длины тени, отбрасываемой объектами, стоящими перпендикулярно к поверхности земли. Тангенс был введен арабским математиком Абу-ль-Вафой в десятом веке. Восточный ученый составил специальные таблицы для определения тангенсов и котангенсов, однако это открытие так и не попало на европейский континент.
В Европе тангенсы были вновь открыты только в XIV веке: немецкий математик Иоганн Мюллер Региомонтан использовал функцию в астрономических расчетах. Термин «тангенс» произошел от латинского слова tanger, что означает «касание» и был введен в обиход в конце XVI века. Данный термин использовался для описания линии тангенсов, то есть касательной к единичной окружности. Региомонтан доказал теорему тангенсов, а также составил специальные таблицы значений функции, которые подошли как для плоской, так и для сферической геометрии.
Определение тангенса
Геометрически тангенс определяется как соотношение противолежавшего катета к прилежащему. Функция всегда рассчитывается для угла и не зависит от длин сторон. Пусть у нас есть треугольник со сторонами A, B и C, где C — гипотенуза. Тангенс угла AC будет рассчитываться как соотношение противолежащего катета B к прилежащему A или tgAC = B/A. Для угла BC тангенс рассчитывается как дробь, в числителе которой длина противолежащего углу катета A к прилежащему B, что математически записывается как tgBC = A/B. Угол AB образуется при двумя катетами, поэтому его невозможно посчитать. Катеты — стороны, образующие прямой угол, поэтому для угла в 90 градусов тангенс не существует.
Помимо геометрического определения, тангенс легко выразить через другие тригонометрические функции. Так, для угла A тангенс можно выразить при помощи отношения синуса и косинуса:
tgA = sinA / cosA.
Наша программа позволяет определить численное значение тангенса для любого значения угла. Для этого достаточно выбрать в меню соответствующую функцию и ввести в ячейку «Угол» величину угла в градусах или радианах. Если необходимо найти угол по известному значению тригонометрической функции, используйте функцию арктангенса. Для этого введите значение тангенса в соответствующую ячейку, после чего калькулятор вернет вам величину угла.
Для этого достаточно выбрать в меню соответствующую функцию и ввести в ячейку «Угол» величину угла в градусах или радианах. Если необходимо найти угол по известному значению тригонометрической функции, используйте функцию арктангенса. Для этого введите значение тангенса в соответствующую ячейку, после чего калькулятор вернет вам величину угла.
Рассмотрим пару примеров
Вычисление угла
Пусть в школьной задаче задан прямоугольный треугольник со сторонами A = 5 см, B = 12 см, C = 13 см. Требуется найти величины всех углов. Итак, очевидно, что угол AB, то есть угол, образуемый двумя катетами — прямой. Это известно из самого определения катетов. Теперь мы можем найти тангенс угла BC, который численно будет равен дроби, в числителе которой противолежащий катет A, а в знаменателе — прилежащий B. Следовательно, tgBC = A/B = 5/12 = 0,416. Зная тангенс, мы легко можем вычислить соответствующий угол при помощи онлайн-калькулятора. Для это выберем в меню функцию тангенса и введем значение 0,416 в ячейку tgα. Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Программа мгновенно отобразит величину угла, равную 22,58 градуса. Вычислить последний угол не составит труда, так согласно постулату о сумме углов треугольника, угол AC = 180 − 90 − 22,58 = 67,42 градуса.
Вычисление тангенса
В школьных задачах чаще всего используются стандартные углы, поэтому школьникам важно знать значения основных тригонометрических функций для этих углов буквально наизусть. Давайте при помощи калькулятора определим значения тангенсов для наиболее распространенных в задачах углов:
- tg30 = 0,577;
- tg45 = 1;
- tg60 = 1,732;
- tg90 — не рассчитывается;
- tg120 = -1,732;
- tg150 = -0,577;
- tg180 = 0.
Выше мы выяснили, почему тангенс не рассчитывается для значений 90 градусов. Еще одно интересное значение — угол в 45 градусов. Почему тангенс равен 1? Ответ очевиден, ведь если в прямоугольном треугольнике один угол равен 45 градусам, то и второй имеет такую же величину. Следовательно, треугольник равнобедренный, его катеты имеют одинаковую длину, а их соотношение в любом случае будет равно 1.
Заключение
Тригонометрия — сложная наука, которая не находит практически никакого применения в повседневной жизни. Однако без тригонометрии не было бы современных технологий, поэтому специалистам прикладных наук без нее никуда. Используйте наши онлайн-калькуляторы для расчета значений тригонометрических функций.
Как использовать Google Sheets: полное руководство
Я не гуру электронных таблиц, но я провел много времени в Google Sheets. От организации ежемесячных маркетинговых материалов в календаре контента с цветовой кодировкой до отслеживания прибыли для моего малого бизнеса, где я перерабатываю одежду — Google Таблицы оказались одним из моих самых любимых инструментов. При эффективном использовании он может упростить процессы и просто облегчить вашу жизнь в целом.
В этой статье я расскажу вам, как использовать Google Таблицы, пройдусь по некоторым полезным формулам и дам вам несколько советов и приемов, которые помогут вам ускорить вашу работу.
Содержание:
Краткий обзор: что такое Google Таблицы?
Обзор: Необходимо знать Google Sheets Условия
- . использование формул в Google Sheets
Дополнительные руководства и советы по Google Sheets
Как делиться, защищать и перемещать свои данные
Бонус: как автоматизировать Google Sheets с помощью Zapier
Краткий обзор: что такое Google Sheets?
Google Таблицы — это приложение для работы с электронными таблицами, к которому вы можете получить доступ через Интернет. Значит ли это, что это всего лишь версия Microsoft Excel от Google? Типа, да не совсем.
Google Sheets — это то же самое, что Excel?
Если вы знакомы с Excel, вам будет легче научиться пользоваться Google Таблицами. Оба они представляют собой приложения для работы с электронными таблицами, поэтому у них много общих функций, но есть несколько важных отличий. Вы можете прочитать о них все в сравнении Zapier с таблицами Google Sheets и Microsoft Excel, но вот основные выводы:
Вы можете прочитать о них все в сравнении Zapier с таблицами Google Sheets и Microsoft Excel, но вот основные выводы:
Google Таблицы были созданы с учетом совместной работы и позволяют легко обмениваться рабочими листами, предоставлять доступ для редактирования и сотрудничать в режиме реального времени. Хотя Excel Online предлагает аналогичные функции совместной работы, они работают не так гладко, как Google Таблицы.
Google Таблицы недавно обновили ограничение на количество ячеек до 10 миллионов, но это все еще меркнет по сравнению с 17 миллиардами ячеек Excel на электронную таблицу. Это делает Excel лучшим инструментом для работы с большими данными. Хорошая новость в том, что Большинство из нас не имеют дело с такими большими наборами данных, поэтому Google Sheets работает просто отлично.
Excel имеет более мощные формулы и функции анализа данных, включая встроенные инструменты статистического анализа и расширенные возможности визуализации данных.
 Google Sheets предлагает «облегченную» версию большинства этих функций, но она далеко не так глубока.
Google Sheets предлагает «облегченную» версию большинства этих функций, но она далеко не так глубока.
Обзор: Обязательные термины Google Таблиц
Для начала давайте рассмотрим некоторые термины электронных таблиц, которые вам необходимо знать при использовании Google Таблиц:
Cell : единственная точка или элемент данных в электронной таблице
Колонка : вертикальный набор ячеек
Row : горизонтальный набор из ячеек
- Диапазон Диапазон . : выбор ячеек, охватывающих строку, столбец или и то, и другое
Функция : встроенная операция из приложения для работы с электронными таблицами, которую вы будете использовать для вычисления значений ячеек, строк, столбцов или диапазонов, управления данными, и более
Формула : Комбинация функций, ячеек, строк, столбцов и диапазонов, используемая для получения конкретного результата ; в одной электронной таблице может быть несколько листов
Электронная таблица: Весь документ, содержащий ваши рабочие листы
1.
 Как создать электронную таблицу
Как создать электронную таблицуСуществует четыре способа создания новой электронной таблицы в Google Sheets:
Вариант 1: Нажмите разноцветную кнопку «+» на панели инструментов Google Sheets.
Вариант 2: Откройте меню из электронной таблицы и выберите Файл > Новый > Электронная таблица .
Вариант 3: Нажмите разноцветную кнопку New на панели инструментов Google Диска и выберите Google Sheets > Пустая таблица .
Вариант 4: Введите в браузере «sheets.new».
Это создаст новую пустую электронную таблицу (или заполненный шаблон, если вы выберете один из них; однако для этого руководства по Google Таблицам вы должны начать с пустой электронной таблицы).
Интерфейс Google Sheets должен напомнить вам по крайней мере еще одно приложение для работы с электронными таблицами, которое вы видели раньше, со знакомыми значками редактирования текста и вкладками для дополнительных листов.
2. Как добавить данные в электронную таблицу
Посмотрите на бело-серую сетку, занимающую большую часть экрана, и первое, что вы заметите, это синий контур вокруг выбранной ячейки или ячеек.
Когда вы откроете новую электронную таблицу, если вы только начнете печатать, вы увидите, что ваши данные сразу же начинают заполнять верхнюю левую ячейку. Нет необходимости дважды щелкать ячейки, когда вы добавляете информацию, и не нужно использовать мышь.
Отдельный квадрат в электронной таблице называется ячейкой ; они организованы в строки и столбцы с числовыми и буквенными идентификаторами соответственно. Каждая ячейка должна содержать одно значение, слово или фрагмент данных.
Не стесняйтесь выбирать любую ячейку, а затем введите что-нибудь. Когда вы закончите вводить данные в ячейку, вы можете сделать одну из четырех вещей:
Нажмите Введите / верните , чтобы сохранить данные и перейти к началу следующей строки.

Нажмите Tab , чтобы сохранить данные и перейти вправо в той же строке.
Используйте клавиши со стрелками на клавиатуре (вверх, вниз, влево и вправо), чтобы переместиться на одну ячейку в этом направлении.
Щелкните любую ячейку, чтобы перейти непосредственно к ней.
Если вы не хотите вводить все вручную, вы также можете массово добавлять данные на лист несколькими способами:
Скопируйте и вставьте список текста или чисел в электронную таблицу.
Скопируйте и вставьте HTML-таблицу с веб-сайта.
Импорт существующей электронной таблицы в форматах CSV, XLS, XLSX и других.
Скопируйте любое значение в ячейке из диапазона ячеек с помощью щелчка и перетаскивания.
Как копировать и вставлять данные
Копирование и вставка не требуют пояснений, но бывают случаи, когда вы пытаетесь скопировать «табличный» набор данных с веб-сайта или PDF-файла, и он просто вставьте в одну ячейку или отформатируйте все в оригинальном стиле. Чтобы не рвать на себе волосы, попробуйте найти данные, которые на самом деле находятся в HTML-таблице (например, данные о фильмах с IMDb), чтобы не получить нелепые вставленные данные в вашу электронную таблицу. Вот видео, показывающее, как копировать и вставлять данные в Google Sheets.
Чтобы не рвать на себе волосы, попробуйте найти данные, которые на самом деле находятся в HTML-таблице (например, данные о фильмах с IMDb), чтобы не получить нелепые вставленные данные в вашу электронную таблицу. Вот видео, показывающее, как копировать и вставлять данные в Google Sheets.
Если вы все же получили странный формат данных, не беспокойтесь: мы исправим это в следующем разделе!
Как импортировать файл
Импортировать файл также просто. Вы можете импортировать непосредственно в текущую электронную таблицу, создать новую электронную таблицу или заменить лист (т. е. отдельную вкладку) импортированными данными.
Чаще всего импортируются файлы CSV (значения, разделенные запятыми) или XLS и XLSX (файлы из Microsoft Excel). Чтобы импортировать файл из-за пределов вашего Google Диска, перейдите к Файл > Импорт > Загрузить . Вот краткий видеоурок, чтобы продемонстрировать, как это сделать.
Я предпочитаю каждый раз импортировать данные на новый лист, чтобы разделять старые и вновь импортированные данные. В качестве альтернативы, если у вас есть Google Sheet (или CSV, XLS или другой файл электронной таблицы), сохраненный в вашей учетной записи Google Диска, вы можете импортировать его непосредственно в свою электронную таблицу, используя тот же процесс — просто выполните поиск на Диске из окна импорта.
В качестве альтернативы, если у вас есть Google Sheet (или CSV, XLS или другой файл электронной таблицы), сохраненный в вашей учетной записи Google Диска, вы можете импортировать его непосредственно в свою электронную таблицу, используя тот же процесс — просто выполните поиск на Диске из окна импорта.
Автозаполнение данных
Перетаскивание для копирования значения ячейки требует небольшого пояснения, потому что вы будете часто использовать его после того, как настроите формулы в своих электронных таблицах.
Перетаскивая маленькую синюю точку (на рисунке ниже) в правом нижнем углу выделенной ячейки через диапазон ячеек или вниз, вы можете выполнять ряд различных задач:
Копирование данных ячейки в соседние ячейки (включая форматирование)
Копирование формулы ячейки в соседние ячейки
Создание упорядоченного списка текстовых данных
Вот пример того, как может работать создание упорядоченного списка.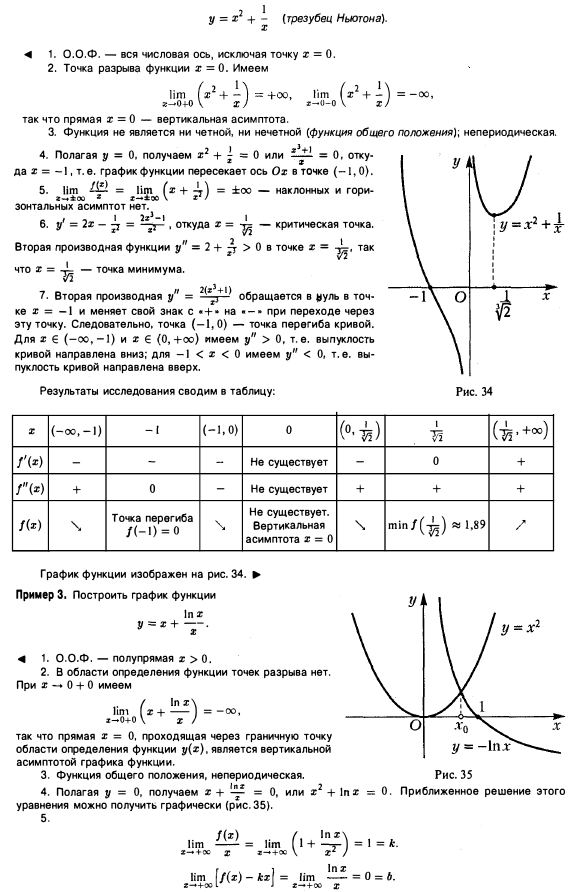 Попробуйте добавить текст «Участник 1» в ячейку A1, затем щелкните и перетащите маленькую синюю точку в правом нижнем углу выделенной ячейки вниз или через любое количество соседних ячеек.
Попробуйте добавить текст «Участник 1» в ячейку A1, затем щелкните и перетащите маленькую синюю точку в правом нижнем углу выделенной ячейки вниз или через любое количество соседних ячеек.
Если после участника не было номера, это действие перетаскивания просто скопирует «участник» во все ячейки, которые вы перетаскиваете. Но поскольку число есть, Таблицы знают, что нужно увеличить следующую ячейку на +1.
Предположим, вы либо скопировали, вставили, импортировали или ввели большой объем данных, и ваша электронная таблица выглядит вполне исправно.
Теперь, как мы можем использовать эти данные?
В дополнение к методам, которые я рассмотрел выше, есть еще способов ручного и автоматического импорта данных в Google Sheets .
3. Как редактировать и форматировать данные для удобства просмотра
Отслеживаете ли вы расходы, записываете оценки или создаете свои список дел , вы захотите манипулировать и форматировать свои данные.
Как использовать панель инструментов Google Таблиц
Основные параметры форматирования в Google Таблицах доступны над первой ячейкой. Они помечены на изображении ниже, но для быстрого ознакомления во время работы с листом просто наведите указатель мыши на значок, чтобы увидеть его описание и сочетание клавиш.
Такие функции, как печать, отмена и повтор действий, настройки шрифта и стиль шрифта, работают так же, как вы ожидаете от своего любимого текстового процессора.
Что касается всего остального, лучший способ показать вам, как все работает, — это погрузиться прямо в пример.
Я собираюсь создать краткий список возможных вариантов завтрака на завтрашнее утро, вместе с их ингредиентами, количеством, ценами и ссылками на видео на YouTube о том, как их приготовить (кто знал, что вы можете снять трехминутное видео о насыпать хлопья в миску?).
В приведенном выше простом примере отсутствие значительного форматирования вполне допустимо. Он выполняет основные функции: хранит мою информацию и позволяет мне ее сохранять. Но это не то, к чему я хотел бы возвращаться каждый день.
Но это не то, к чему я хотел бы возвращаться каждый день.
Так как я завтракаю каждое утро, давайте потратим некоторое время на то, чтобы сделать эту таблицу более удобной для пользователя, немного отформатировав ее.
Как зафиксировать строки и столбцы
Работая с той же электронной таблицей, мы зафиксируем первую строку на месте. Это означает, что если мы прокрутим электронную таблицу вниз, первая строка все равно будет видна, независимо от того, сколько данных находится под ней. Это позволяет вам иметь длинный список и помогает следить за тем, что вы на самом деле просматриваете.
Есть два способа закрепить строки:
Нажмите Вид > Закрепить > 1 строка на панели навигации, чтобы зафиксировать первую строку на месте.
Наведите указатель мыши на темно-серую полосу в верхнем левом углу электронной таблицы (пока она не превратится в руку) и перетащите ее между строками 1 и 2.
Замораживание строки заголовка — это первое, что я лист делаю.
Как скрыть строки и столбцы
Теперь скажем, например, что у вас закончился хлеб, поэтому французские тосты больше не вариант. Чтобы временно скрыть этот столбец из списка, щелкните правой кнопкой мыши Столбец C и нажмите Скрыть столбец .
Как форматировать текст
Теперь давайте сделаем текст заголовка всплывающим с помощью простого форматирования текста (помните, что инструменты форматирования текста находятся на панели инструментов, прямо над первой строкой):
Перетащите, чтобы выбрать ячейки, хочу отформатировать
Выделить текст жирным шрифтом
Увеличить размер шрифта до 12 пунктов
Выровнять всю строку по центру
Закрасьте свои ячейки серым цветом
Следующее, что я сделаю, чтобы немного почистить это, это отформатировать мою «Среднюю цену / порцию» в долларовом выражении. Выделите строку, а затем щелкните значок знака доллара, чтобы отобразить выбранные ячейки в виде суммы в долларах, а не в виде обычного числа.
Как добавить лист
Теперь предположим, что вы хотите составить похожий список на завтрак и ужин. Вместо создания новой электронной таблицы нажмите кнопку «+» в левом нижнем углу, чтобы добавить дополнительные листы.
4. Как использовать формулы в Google Sheets
В Google Sheets, как и в большинстве приложений для работы с электронными таблицами, есть набор встроенных формул для выполнения ряда статистических задач и задач по обработке данных. Вы также можете комбинировать формулы для создания более мощных вычислений и объединения задач. Если вы уже привыкли работать с числами в Excel, точно такие же формулы работают в Google Sheets большую часть времени .
В этом руководстве мы сосредоточимся на пяти наиболее распространенных формулах, которые отображаются в раскрывающемся меню формул в верхней части навигации.
Вы можете щелкнуть формулу, чтобы добавить ее в ячейку, или вы можете начать вводить любую формулу со знаком равенства (=) в ячейке, за которым следует имя формулы. Таблицы будут автоматически заполнять или предлагать формулы на основе того, что вы вводите, поэтому вам не нужно запоминать каждую формулу.
Таблицы будут автоматически заполнять или предлагать формулы на основе того, что вы вводите, поэтому вам не нужно запоминать каждую формулу.
Самые основные формулы в Таблицах включают:
СУММ : суммирует диапазон ячеек (например, 1+2+3+4+5 = сумма 15)
СРЕДНЕЕ 90 с среднее значение диапазона ячеек (например, 1, 2, 3, 4, 5 = среднее значение 3)
COUNT : подсчитывает значения в диапазоне ячеек (например, 1, пусто, 3, 4, 5 = всего 4 ячейки со значениями)
MAX : находит наибольшее значение в диапазоне ячеек (например, 1, 2, 3, 4, 5 = 5 является самым высоким)
MIN : находит наименьшее значение в диапазоне ячеек (например, 1,2,3,4,5 = 1 — самый низкий)
Мы изучим эти формулы, улучшив нашу таблицу завтраков.
СУММ формула
=СУММ(диапазон)
Начнем с суммирования общего количества ингредиентов, необходимых для каждого рецепта.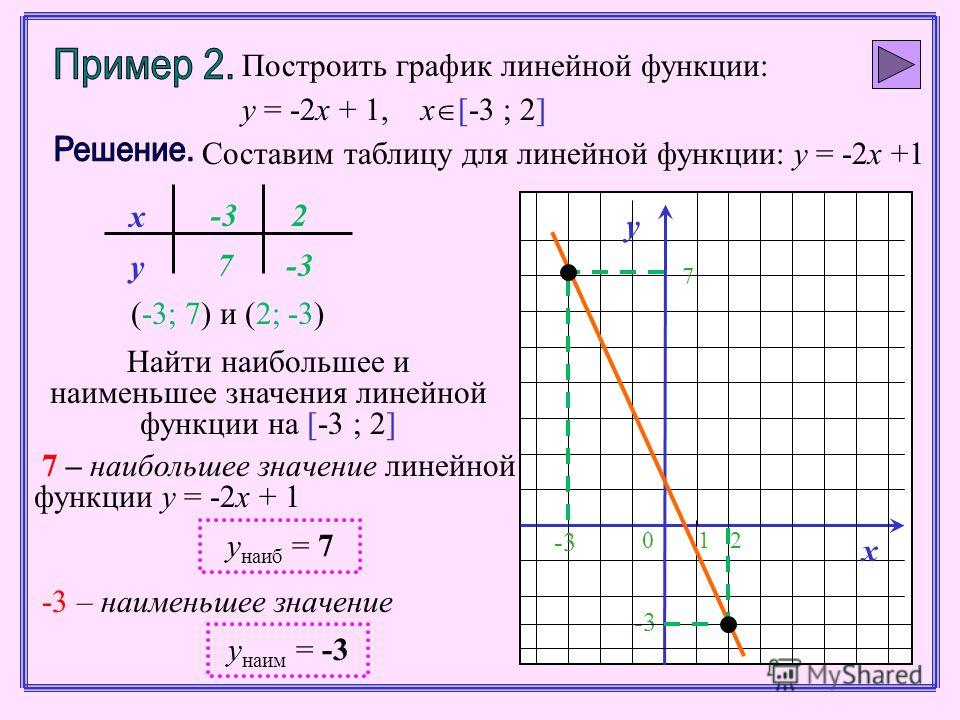 Я буду использовать формулу СУММ, чтобы добавить каждое значение в рецептах и получить общую сумму.
Я буду использовать формулу СУММ, чтобы добавить каждое значение в рецептах и получить общую сумму.
Существует три способа использования основных формул, доступных через верхнюю навигацию:
Выберите диапазон, затем щелкните формулу (это поместит результат либо ниже, либо сбоку от диапазона).
Выберите ячейку результата (т. е. ячейку, в которой должен появиться результат), затем щелкните формулу, которую хотите использовать, на панели инструментов. Наконец, выберите диапазон ячеек для выполнения операции.
Введите формулу в ячейку результатов (не забудьте знак =), затем введите диапазон вручную или выберите диапазон.
Я продемонстрирую все три метода в видеоуроке здесь. Во-первых, я суммирую свои ингредиенты, выбрав диапазон и щелкнув СУММ в меню формул. Во-вторых, я выберу ячейку результата и выделю диапазон ячеек, которые будут суммироваться. Наконец, я продемонстрирую ввод формулы и диапазона вручную. Когда вы закончите выбирать ячейки, которые хотите сложить, нажмите Введите / верните .
Когда вы закончите выбирать ячейки, которые хотите сложить, нажмите Введите / верните .
Теперь, когда есть формула, настроенная для суммирования всех ингредиентов, вы можете выбрать ячейку с формулой и перетащить синюю точку на другие ячейки, чтобы скопировать формулу в эти ячейки.
Формула СЧЕТА
=СЧЁТ(диапазон)
Теперь, когда мы знаем, сколько частей требуется для каждого рецепта, я хотел бы знать, насколько сложно это сделать. Я упростил это, предполагая, что меньшее количество ингредиентов означает, что рецепт менее сложен.
Чтобы подсчитать количество ингредиентов в каждом рецепте, я буду использовать формулу СЧЁТ. Формула COUNT, по сути, проверяет, пусты ли ячейки в диапазоне, и возвращает общее количество заполненных ячеек. Эта формула будет настроена в моей электронной таблице так же, как моя строка СУММ. Смотрите туториал.
Согласно моей таблице, хлопья — самый простой завтрак, но я все еще не уверен, что легкий завтрак того стоит.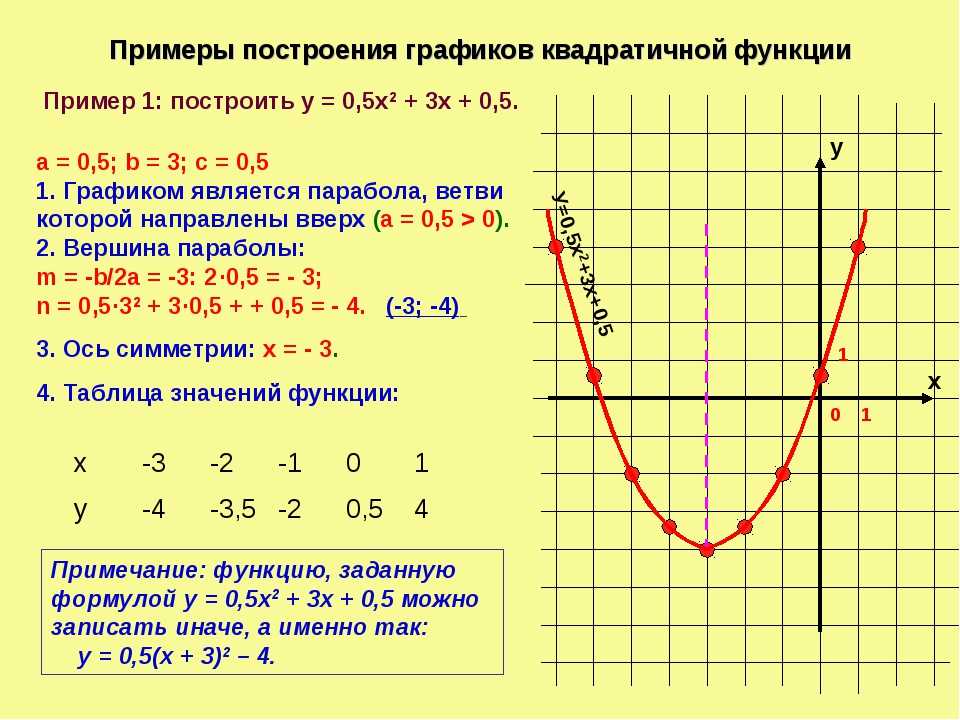 Что делать, если это стоит слишком дорого? Что, если дополнительные усилия по приготовлению другого блюда сэкономят мне деньги?
Что делать, если это стоит слишком дорого? Что, если дополнительные усилия по приготовлению другого блюда сэкономят мне деньги?
Теперь я собираюсь уточнить свое решение, рассчитав среднюю стоимость порции завтрака по формуле СРЕДНЕГО.
СРЕДНЯЯ формула
=СРЕДНЯЯ(диапазон)
Я добавил ложные минимальные и максимальные цены за единицу в списке ингредиентов справа от вариантов завтрака. Мы хотим получить среднюю цену для каждого ингредиента, используя низкие и высокие ставки.
Я начну с выделения диапазона значений (в данном случае это два ряда, а не вертикальный диапазон) и выбора формулы СРЗНАЧ на панели инструментов.
Это переместит результат в столбец справа от столбца максимальной цены. Затем я перетащу формулу вниз, чтобы применить ее к остальной части списка. Смотрите как здесь.
Я назову свой столбец «Средняя стоимость единицы», чтобы мы знали, на что смотрим.
Формула MIN
Допустим, я хотел определить самую низкую цену за единицу опций.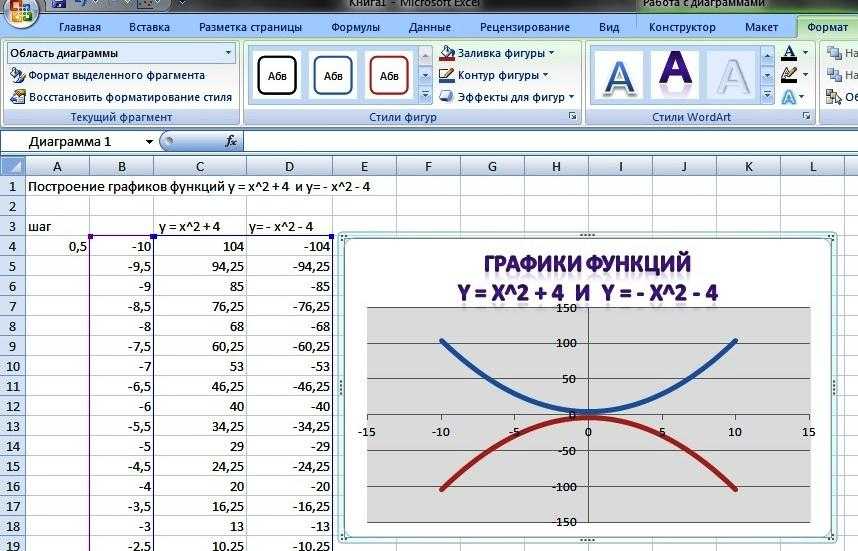 Хотя вы можете легко просто посмотреть на диаграмму и выбрать ее, эта формула очень полезна для больших наборов данных и избавит вас от бесконечной прокрутки. Посмотрите, как я использую эту формулу здесь.
Хотя вы можете легко просто посмотреть на диаграмму и выбрать ее, эта формула очень полезна для больших наборов данных и избавит вас от бесконечной прокрутки. Посмотрите, как я использую эту формулу здесь.
Формула MAX
Точно так же, если бы я хотел определить самую высокую цену за единицу опционов, я бы использовал формулу MAX. Посмотрите, как я использую эту формулу здесь.
После того, как вы освоите приведенные выше формулы, функций Google Sheets нужно будет изучить множество других функций.
5. Дополнительные руководства и советы по работе с Google Sheets
Теперь, когда вы знаете, как создавать электронные таблицы, импортировать данные и использовать формулы, я дам вам несколько дополнительных советов.
Как создать сводную таблицу
Сводная таблица — это удобный способ анализа и визуализации данных. Чтобы создать сводную таблицу, выполните следующие действия:
Перейдите к Вставьте > Сводная таблица .

В редакторе сводной таблицы добавьте выбранные значения строки и столбца.
Рядом с Values нажмите Add, и выберите нужное значение в раскрывающемся меню (вы также можете выбрать один из предложенных вариантов сводной таблицы).
В этом примере я создал искусственный набор данных и использовал сводную таблицу, чтобы показать средние баллы обучения каждого отдела.
Помимо этого краткого руководства, существует множество различных способов создания и использования сводных таблиц в Google Sheets .
Как использовать ярлыки для экономии времени
При использовании Google Таблиц ярлыки могут помочь вам сэкономить время и работать быстрее. Я перечислил некоторые из моих наиболее часто используемых ярлыков ниже.
Command | Shortcut |
|---|---|
Cut | Control + X / command + X |
Copy | Control + C / command + C |
Вставить | Control + V / команда + V |
Отменить Control + Z команда50003 | |
Redo | Control + Y / command + Y |
Select an entire row | Shift + Spacebar |
Select an entire column | Control + Пробел / команда + Пробел |
Как создавать диаграммы и графики
Важным этапом анализа данных является визуализация ваших данных, и Google Таблицы могут помочь вам сделать это с помощью диаграммы и графики . Просто выделите необходимые данные и нажмите Insert > Chart . Диаграмма будет создана, и вы можете редактировать ее по своему усмотрению на боковой панели.
Просто выделите необходимые данные и нажмите Insert > Chart . Диаграмма будет создана, и вы можете редактировать ее по своему усмотрению на боковой панели.
Вы можете поэкспериментировать с различными типами диаграмм и найти тот, который лучше всего подходит для вашего набора данных.
Zapier позволяет автоматически создавать диаграммы и отчеты в Google Sheets .
Как делиться, защищать и перемещать данные
Что делает Таблицы такими мощными, так это то, насколько синхронно вы будете чувствовать себя со своими коллегами. Совместное редактирование электронной таблицы — одна из важнейших функций Таблиц, и Google сделал ее удобной.
Вот как это работает:
Щелкните либо Файл > Поделиться , либо используйте зеленую кнопку Поделиться в правом верхнем углу.
Введите адреса электронной почты тех, кто может просматривать или редактировать вашу электронную таблицу.

Выберите другие параметры конфиденциальности и нажмите Готово .
После того, как вы добавите людей, с которыми хотите поделиться, вы можете предоставить им доступ к просмотру, комментированию или редактированию. Вы также можете добавить срок действия, если вы принимаете комментарии только в течение ограниченного времени.
Помимо предоставления общего доступа определенным людям, вы также можете предоставить общий доступ всем в вашей организации или всем, у кого есть ссылка.
Совместное использование электронных таблиц с вашими устройствами и приложениями
Несмотря на то, что Google Таблицы созданы для совместного использования между пользователями, вы часто замечаете, что ваши электронные таблицы создаются как внутренние документы, а совместное использование является второстепенным по отношению к фактическому выполнению работы.
Вы можете оптимизировать рабочие процессы электронных таблиц и обмен данными в режиме реального времени, воспользовавшись этими полезными надстройками:
Мобильные приложения Google Sheets.
 Мобильное приложение Google Таблицы можно использовать для просмотра и редактирования электронных таблиц, обмена ссылками на ходу и добавления пользователей. Это надежное дополнение к веб-приложению, но не его замена.
Мобильное приложение Google Таблицы можно использовать для просмотра и редактирования электронных таблиц, обмена ссылками на ходу и добавления пользователей. Это надежное дополнение к веб-приложению, но не его замена.Google Диск . Google Диск позволяет легко загружать файлы из локальной среды рабочего стола на онлайн-Диск. Это делает их доступными для ваших сотрудников, а также позволяет быстро импортировать их в электронные таблицы и другие документы.
Сторонний инструмент, такой как Zapier. Вы можете использовать Zapier для автоматического добавления данных в ваши электронные таблицы, отправки файлов в вашу учетную запись Google Диска, оповещения об изменениях в ваших Таблицах — вы называете это.
Как загрузить данные
Если вам нужно отправить файлы внешним соавторам, загрузить файл в другую систему или просто создать резервную копию, воспользуйтесь одним из многочисленных вариантов экспорта данных Google Sheets.
Чаще всего экспортируется в формате XLS (документ Excel), PDF или CSV (значения, разделенные запятыми). Если вы не уверены, какой формат использовать, лучше всего подойдет CSV.
Используйте электронную таблицу в автономном режиме
Google Таблицы имеют автономный режим, который автоматически синхронизирует ваши изменения в документе при повторном подключении к Интернету. Это полезно в любой ситуации, когда вам нужно обращаться с Google Sheets как с настольным приложением — например, в полете или в поездке.
Вам понадобится:
Google Chrome
Google Drive Chrome Web App
Google Drive Sync
Инструкции по настройке автономной синхронизации действительно просты, но основная часть процесса заключается в загрузке и использовании трех основных компонентов, указанных выше.
Перейдите к Файл > Сделать доступным в автономном режиме , чтобы включить его.
Точно так же вы можете использовать Google Sheets даже в автономном режиме — Wi-Fi не требуется.
7. Бонус: как автоматизировать Google Таблицы с помощью Zapier
Google Таблицы — это мощный инструмент. В нем есть все, что вы ожидаете от электронной таблицы, с дополнительными возможностями онлайн-приложения. Хотя пример электронной таблицы, который мы создали, может быть немного глупым, практическое применение Таблиц для ваших рабочих процессов (как деловых, так и личных) безгранично.
Как только вы освоите Google Таблицы, используйте Zapier для автоматизации конкретных задач, таких как сохранение URL-адресов , создание событий Календаря Google и многое другое. В зависимости от вашей отрасли есть и другие очень специфические вещи, которые вы можете сделать, например:
Автоматически добавление подписчиков в MailChimp от Google Sheets
Автоматические обновления инвентаризации
Connect Google Sheets с Save Shophys 9003
- 9
- 999999999999999999999999999999999999.

Благодаря тому, что все хранится на Google Диске, вы больше никогда не будете беспокоиться о потере файлов, даже если ваш компьютер выйдет из строя.
Эта статья была первоначально опубликована Майклом Граббсом в июле 2016 года. Последнее обновление было в марте 2023 года.
Калькулятор цен на облигации | Формула
С помощью этого калькулятора цен на облигации мы стремимся помочь вам рассчитать стоимость облигаций, выпущенных правительством или корпорацией . Выяснение текущей цены облигации является одной из наиболее важных процедур для инвесторов в облигации, поскольку просчеты могут привести к огромным потерям. Но не беспокойтесь, этот калькулятор создан для того, чтобы облегчить вам этот процесс.
Мы написали эту статью, чтобы помочь вам понять что такое цена облигации и как определить цену облигации, используя формулу цены облигации . Мы также продемонстрируем несколько примеров, чтобы помочь вам понять концепцию.
Что такое цена облигации? Понимание динамики уравнения цены облигации
Прежде чем мы углубимся в расчет текущей цены облигации с помощью нашего калькулятора оценки, давайте поговорим о том, что такое облигация. Облигация является одним из наиболее распространенных ценные бумаги с фиксированным доходом . Когда предприятие выпускает облигации, это считается получением финансирования от инвесторов посредством выпуска долговых обязательств . Рынок облигаций может быть не так известен, как фондовый рынок, но, хотите верьте, хотите нет, глобальный рынок облигаций более чем вдвое превышает фондовый рынок .
Когда вы покупаете облигацию у эмитента облигаций, вы, по сути, предоставляете кредит эмитенту облигаций . Поскольку цена облигации представляет собой сумму денег, которую инвесторы платят за приобретение облигации, она является одним из наиболее важных, если не самым важным, показателем оценки облигации.
Теперь давайте рассмотрим несколько примеров, чтобы понять, как рассчитывать цены облигаций.
Как рассчитать цену облигации? Формула цены облигации
Цена облигации рассчитывается как текущая стоимость денежного потока, генерируемого облигацией, а именно купонного платежа в течение всего срока действия облигации и основного платежа или платежа в конце срока облигации. . Вы можете увидеть, как она меняется со временем, на графике цены облигации в нашем калькуляторе.
Чтобы использовать уравнение цены облигации, вам необходимо ввести следующие данные в наш калькулятор текущей цены облигации:
-
Номинальная стоимость— Номинальная стоимость купона; -
Ставка купона— Годовая ставка купона; -
Частота— Частота выдачи купона, т.е. количество раз распространения купона в году; -
n— Годы до погашения; и -
YTM— Доходность к погашению.
В качестве примера возьмем облигацию А, выпущенную компанией «Альфа». Он имеет следующие данные:
- Номинальная стоимость: 1000 долларов
- Годовая купонная ставка: 5%
- Периодичность купонов: ежегодно
- Срок погашения: 10 лет
- Доходность к погашению (YTM): 8%
Калькулятор оценки облигаций выполняет следующие шаги:
Определить номинал .
Номинальная стоимость
лицо = 1000 долларов.Рассчитать купон за период .
Для расчета купона
за периодвам потребуются два входа, а именно купонная ставкаМожно рассчитать по следующей формуле:
купон за период = номинальная стоимость * купонная ставка / частотаПоскольку это годовая облигация, частота
 А купон
А купон (1000 долл. США * 5%) / 1 = 50 долл. США.Определить годы до погашения .
n— это количество лет, которое проходит с текущего момента до момента погашения облигации.nдля облигации A составляет10 лет.Определить доходность к погашению (YTM) .
YTM— это годовая норма прибыли, которую получит инвестор в облигации, если он будет держать облигацию с настоящего момента до наступления срока ее погашения. В этом примере 9{10}}цена облигации=(1+8%)1 50 долларов США+(1+8%)250 долларов США+(1+8%)3 50 долларов +…+(1+8%)9 50 долларов США +(1+8%)10$1,050В конце концов, окончательный результат:
`цена облигации = 798,70$`
В нашем калькуляторе цен на облигации вы можете следить за текущей стоимостью платежей на графике цен на облигации за определенный период.

Результаты калькулятора цен на облигации — еще немного информации
Теперь, когда вы понимаете значение цены облигации и то, как ее найти. Вот несколько идей, которыми мы хотели бы поделиться с вами:
Цены на облигации сильно зависят от макроэкономической среды , особенно процентных ставок . Когда центральные банки, такие как Федеральная резервная система и Банк Англии, меняют свою политику процентных ставок, цены на облигации колеблются. В частности, цена облигации увеличивается, когда процентные ставки снижаются, и наоборот.
Цены облигаций могут быть как выше, так и ниже их номинальной стоимости. Это зависит от купонных ставок и рисков облигации. Чем выше купонная ставка, тем выше цена при неизменности всех остальных параметров. Чем выше риск облигации, тем ниже ее цена при неизменности всех остальных параметров.
Корпоративные облигации, как правило, более рискованны, чем аналогичные государственные облигации.
 Это связано с тем, что корпоративные облигации связаны с кредитным риском, так как они могут погасить . Большинство государственных облигаций менее чувствительны к кредитным рискам, поскольку большинство из них могут напечатать больше денег для погашения своего долга.
Это связано с тем, что корпоративные облигации связаны с кредитным риском, так как они могут погасить . Большинство государственных облигаций менее чувствительны к кредитным рискам, поскольку большинство из них могут напечатать больше денег для погашения своего долга.
Вот несколько калькуляторов облигаций, которые могут вас заинтересовать:
- калькулятор доходности облигаций Калькулятор доходности облигаций 9Калькулятор доходности эквивалента облигации 0011
- Калькулятор ставки купона
Часто задаваемые вопросы
Что такое облигация?
Облигация представляет собой долговую ценную бумагу , обычно выпускаемую государством или корпорацией и продаваемую инвесторам . Инвесторы ссужают деньги эмитенту облигаций, покупая облигации. Инвесторы будут получать прибыль, получая купоны в течение всего срока действия облигации и номинальную стоимость по истечении срока облигации.
Что такое купон?
Купон выплата процентов по облигации . Как правило, он распределяется ежегодно или раз в полгода в зависимости от облигации. Обычно он рассчитывается как произведение купонной ставки и номинальной стоимости облигации.
Что такое YTM?
YTM означает доходность к погашению облигации . Это доходность, которую получат инвесторы в облигации, если они будут держать облигацию до погашения .
Какая номинальная стоимость?
Номинальную стоимость облигации также можно назвать основной . Это сумма денег, которую инвестор в облигации получит на дату погашения, если эмитент облигаций не объявит дефолт . Это последний платеж, который получит инвестор в облигации, если облигация удерживается до погашения.
Если процентные ставки вырастут, что произойдет с ценами на облигации?
Если процентные ставки вырастут, то будет YTM облигации .
 Google Sheets предлагает «облегченную» версию большинства этих функций, но она далеко не так глубока.
Google Sheets предлагает «облегченную» версию большинства этих функций, но она далеко не так глубока.


 Мобильное приложение Google Таблицы можно использовать для просмотра и редактирования электронных таблиц, обмена ссылками на ходу и добавления пользователей. Это надежное дополнение к веб-приложению, но не его замена.
Мобильное приложение Google Таблицы можно использовать для просмотра и редактирования электронных таблиц, обмена ссылками на ходу и добавления пользователей. Это надежное дополнение к веб-приложению, но не его замена.

 А купон
А купон 
 Это связано с тем, что корпоративные облигации связаны с кредитным риском, так как они могут погасить . Большинство государственных облигаций менее чувствительны к кредитным рискам, поскольку большинство из них могут напечатать больше денег для погашения своего долга.
Это связано с тем, что корпоративные облигации связаны с кредитным риском, так как они могут погасить . Большинство государственных облигаций менее чувствительны к кредитным рискам, поскольку большинство из них могут напечатать больше денег для погашения своего долга.
Ваш комментарий будет первым