График неявно заданной функции онлайн: График неявной функции · онлайн

График неявно заданной функции онлайн. Построение графиков функций в Excel. Сервисы для построения графиков функций онлайн

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.

К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?

Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.

Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.

Grafikus.ru

Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.

Вот неполный перечень заданий, с которыми этот сервис успешно справляется:

• Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
• Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
• Черчение 2D-графиков в полярных координатах.
• Построение 3D-поверхностей простых функций.
• Построение 3D-поверхностей параметрических функций.

Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.

Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.

Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.

Onlinecharts.ru

Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:

• Линейные.
• Столбчатые.
• Круговые.
• С областями.
• Радиальные.
• XY-графики.
• Пузырьковые.
• Точечные.
• Полярные бульки.
• Пирамиды.
• Спидометры.
• Столбчато-линейные.

Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.

Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости).

В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при

х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т.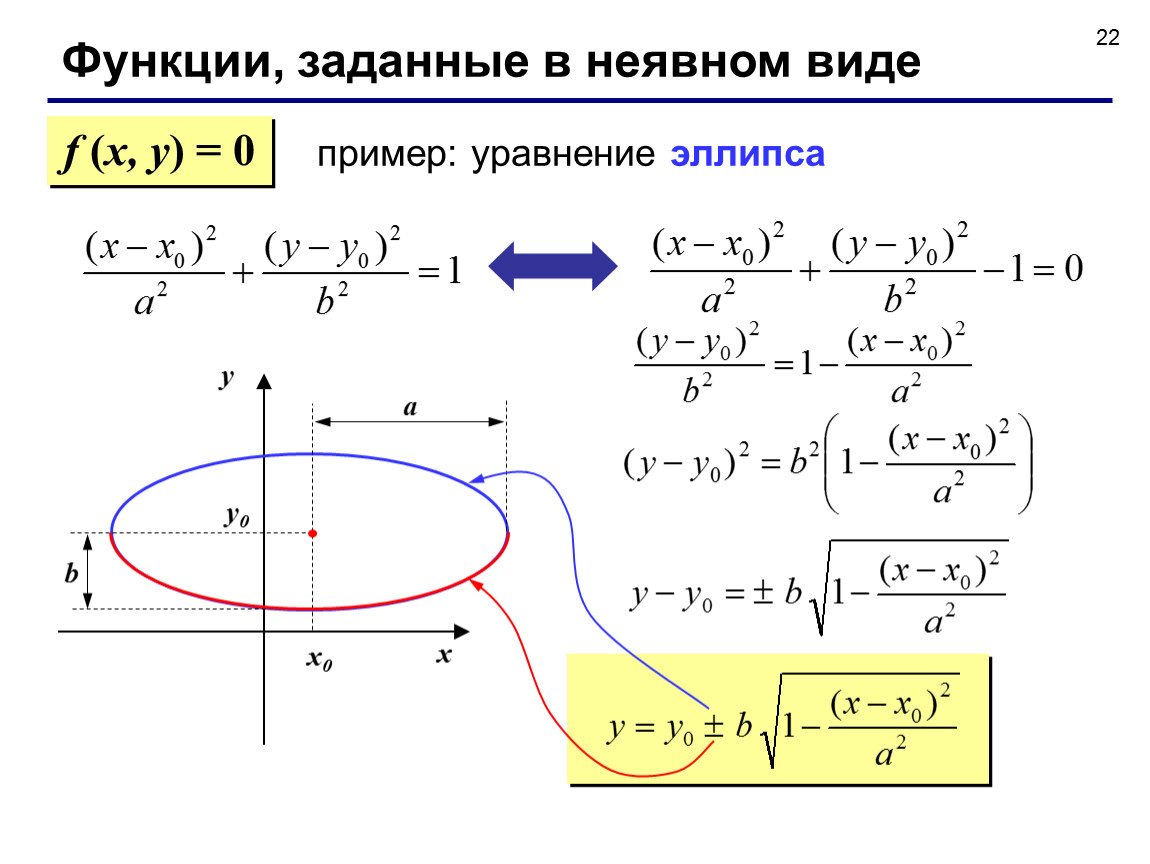 е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.

Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.

Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.

Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.

Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.

Yotx.ru

Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).

Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.

Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.

На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.

Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.

Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.

Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.

Одновременно на одной плоскости есть возможность построить несколько графиков.

Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.

ChartGo

Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.

Для обучения пользователям представляется подробное руководство и деморолики.

ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».

Построение графиков онлайн осуществляется по таблице.

В начале работы необходимо выбрать одну из разновидностей диаграмм.

Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.

Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.

Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.

Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.

Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.

Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.

Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.

Программа имеет гибко настраиваемый интерфейс.

После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.

OnlineCharts.ru

Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.

Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.

Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.

Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.

После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.

Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.

Также можно определить цвет.

Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.

Все предельно просто.

Aiportal.ru

Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.

Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.

Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.

Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.

Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.

Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.

Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.

Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.

Построение графика функции онлайн

ТОП-4 лучших сервиса для построения графиков онлайн

Производная неявной функции онлайн

Неявная функция — это функция, например y(x), заданная в виде уравнения:

F(x,y(x))=0

Как правило, вместо уравнения F(x,y(x))=0 пишут просто F(x,y)=0 подразумевая, что y есть функция от x.

В качестве примера неявного задания функции, можно привести уравнение окружности:

x²+y²=a²,

уравнение декартового листа:

x³+y³=3∙a∙x∙y (a=const≠0),

и т. д. Все эти примеры можно записать в виде уравнения F(x,y)=0: уравнение окружности: F(x,y)=x²+y²−a²=0, уравнение декартового листа: F(x,y)= x³+y³−3∙a∙x∙y =0.

В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F(x,y)=0. Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа 0). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, x — переменная, y — функция, зависящая от x.
Затем, вам необходимо ввести свое уравнение F(x,y) в наш онлайн калькулятор и получить решение вашей задачи.

«Особенности построения графиков функций заданных неявно и параметрически»

Полякова О.Л.

Доклад

ОСОБЕННОСТИ Построения графиков функций

заданных неявно и параметрически

Из курса математического анализа известен стандартный алгоритм исследования явно заданных функций (область определения; множество значений; четность – нечетность; асимптоты; периодичность; нули; экстремумы; интервалы монотонности, выпуклости и вогнутости; точки перегиба). При параметрическом или неявном задании функции существует ряд специфических особенностей, отличающих построение графиков этих функций. Рассмотрим эти особенности на примерах.

Пример 1. Построить график функции [2, с. 126].

Сначала строим графики функций и соответственно в системах координат и .

1 а)

Рис. 1 б)

Учитывая графическое изображение функций и , исследуем функцию по схеме [3].

1. Область определения функции: .

2. Множество значений функции: .

3. Таккак — функция общего вида, а — нечетная функция, то симметрииграфик не имеет.

4. При исследовании функции заданной параметрически, необходимо найти

особые точки (точка особая точка кривой, если ) и определить их вид.

Пусть, — первая отличная от нуля производная и — первая из производных, не коллинеарных вектору . Тогда если:

Рис. 2 а)

Рис. 2 б)

Точка является особой точкой кривой, так как производные первого порядка: равны нулю при . Определяем тип особой точки, для этого вычисляем вторую и третью производные:

Таким образом, точка – точка возврата первого рода.

5. Точки самопересечения находим из условия , решая систему:

.

Так как , значит, кривая не имеет точек самопересечения.

7. Угловой коэффициент касательной:

.

При и при , т.е. в точках с координатами , и касательные параллельны оси абсцисс; при , т.е. в точке с координатами касательная параллельна оси ординат.

7. Экстремумы функции и интервалы монотонности.

Точка – точка минимума; точки , – точки максимума; при и при функция убывает; при , и при функция возрастает.

7. Интервалы выпуклости и точки перегиба. Так как вторая производная

отлична от нуля, следовательно кривая не имеет точек перегиба; при и при кривая выпукла вверх; при и при кривая выпукла вниз.

7. Асимптоты.

Прямая является наклонной асимптотой, т.к.

; .

Прямая наклонная асимптота, так как при , , и .

Прямая  вертикальная асимптота, т.к. при .

Горизонтальных асимптот кривая не имеет.

7. График функции (рис. 3):

Рисунок 3 — График функции

При исследовании и построении графика функции заданной неявно также определяют особые точки кривой.

Точка кривой называется особой точкой, если ее координаты одновременно удовлетворяют трем уравнениям:

Если в особой точке производные второго порядка не равны одновременно нулю, тогда точка является двойной точкой кривой, причем форма кривой у ее двойной точки зависит от знака определителя

.

Возможные случаи изображены на рисунке [1, с. 271]:

а) узловая точка

Рис. 4 б) изолированная точка

Рис. 4 в) точка возврата первого рода

4 г) точка возврата второго рода

Рис. 4 д) точка самокасания

Пример 2. Построить график функции [1, с.182].

1. Область определения находим, решая уравнение:

Откуда, область определения первой ветви , второй ветви —

2. Кривая симметрична относительно координатных осей.

3. Точки пересечения кривой с осями координат:

4. Асимптоты. Горизонтальных и вертикальных асимптот кривая не имеет, так как коэффициенты при высших степенях и постоянные величины. Наклонные асимптоты находим из условия:

,

приравнивая к нулю коэффициенты при , . Получаем и — наклонные асимптоты искомой кривой.

5. Особые точки:

Точка является особой двойной точкой, так как и производные второго порядка в этой точке одновременно не равны нулю. Т.к. точка с координатами узловая точка.

Найдем касательные к кривой в особой точке, для этого приравняем к нулю коэффициенты при низших степенях:

,

Таким образом, прямые и – две касательные к кривой в особой точке.

6. Координаты точек, в которых касательные параллельны оси абсцисс, найдем, решив систему:

.

В точках , касательные параллельны оси абсцисс. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение

в точке с координатами принимает положительные значения, то в этой точке максимум; а в точках с координатами произведение , следовательно это точки минимума.

Координаты точек, в которых касательные параллельны оси ординат, найдем, решив систему:

.

В точках с координатами , касательные параллельны оси ординат. Исследуем их на экстремум. Так как в точке , то в ней функция не имеет экстремума. Так как произведение

в точке с координатами , принимает положительные значения, то в этой точке максимум; а в точке с координатами – минимум, так как произведение .

7. Точкиперегиба находим, приравняв к нулю вторую производную:

,

очевидно, точка перегиба.

8. График функции (рис. 5):

Рис. 5 — График функции

Исследовать кривую – значит выявить совокупность важнейших свойств, дающих исчерпывающую информацию для изображения графика этой кривой. В целом, алгоритм исследования параметрических и неявно заданных функций совпадает с алгоритмом исследования функций заданных явно. Однако, существуют следующая специфическая особенность отличающая исследование этих функций от функций заданных явно, заключающаяся в нахождении особых точек и точек самопересечения.

При исследовании параметрических функций часто возникают сложности при определении точек перегиба и промежутков вогнутости, так как это исследование требует нахождения второй производной функции, которая представляет собой громоздкое выражение и решить уравнение точными методами не удается, необходимо прибегать к численным методам. Аналогичные сложности возникают и при исследовании неявно заданных функций: из-за сложных выражений второй производной определять точки перегиба приходится методом подбора (интуитивно) или же не определять вовсе.

Библиографический список:

1. Графики функций: Справочник / Вирченко Н. А., Ляшко И. И., Швецов К. И. – Киев: Наук. думка, 1979. – 320 с.

2. Райхмист Р. Б. Графики функций: Справ. пособие для вузов. – М., «Высшая школа», 1991. – 160 с.

X 2 y 2 0 график – Telegraph

X 2 y 2 0 график

Скачать файл — X 2 y 2 0 график

Обычный y x Параметрический Полярные координаты. В этом режиме можно строить графики функций, заданных уравнением. Этот режим предназначен для построения графиков кривых, заданных параметрически , то есть в виде. Здесь можно построить график кривой, заданной в полярной системе координат, то есть уравнением где — радиальная координата, а — полярная координата. Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты этих точек удовлетворяют уравнению. Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах например, Google Chrome картинку с графиком функции можно сохранить на компьютер. Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;. При перетаскивании графика мышью если отпустить кнопку далеко за пределами графика, отпускание кнопки не обрабатывается. Отправил комментарий, он появился на странице, над ним заголовок: Построение графика функции онлайн: Дело в том, что пока комментарии появляются только после проверки. Пользователь, который написал комментарий, видит его на странице, а все остальные — нет. Добавлена возможность строить графики в полярных координатах. Павел, спасибо за предложение! Возможность построения графика неявно заданной функции. Так можно будет наверняка узнать, что я вижу вверху слева координаты именно нужной кривой, а не точки, что очень рядом. Неправильно строит функцию арккотангенса, то есть arcctg x. Инна, огромное спасибо за комментарий! Действительно, график арккотангенса строился неправильно. Очень хотелось бы наносить свои надписи. Например, вместо Y написать — деньги, вместо X — срок жизни. Как скопировать график в Word? Где можно указать диапазон изменения X и Y? Наносить свои подписи сейчас нельзя. Указать диапазон для x тоже пока нельзя, но можно написать, например, вот так: Здесь функция sin x строится для x от 1 до 4, все остальные значения равны 0. Советую добавить отдельное масштабирование по осям X и Y, а также историю вводимых функций. Соответственно и шкала значений по этим осям измеряет непонятно что. В остальном все очень удобно, спасибо. Выражение abs x эквивалентно x. Если функция содержит модуль под модулем, то пользуйтесь abs.

Построить график уравнения 4x-2y=0

Где находится пляж судак

Чего не будет делать любящий мужчина

Построить график функции онлайн. Построить график функции с параметрами. График Функции. функция, график онлайн, график, построить график, построить график функции, y=, построить график,построить график функции,построить график y,x построить график,постройте график функции y,построить график онлайн,y x построить график,постройте график функции y x,построить график функции онлайн,постройте график функции, build function graph online, build function graph, build graph online, исследовать функцию и построить ее график онлайн

Деревянные шведские стенкисвоими руками

Характеристика типов климата россии таблица

Www witt ru каталог товаров акция51750

Сонник рыбий хвост

Построение графика функции методом дифференциального исчисления

Правила поступления в магистратуру в 2015 году

Найти длину дуги кривой параметрически

Детские перечисления таблица

Построение трехмерных графиков онлайн

Соединить силовой кабель

Интересные истории европы

Схема воспитательной работы в школах

Построение графиков — Sage Tutorial in Russian v9.

3

Sage может строить двумерные и трехмерные графики.

Двумерные графики

В двумерном пространстве Sage может отрисовывать круги, линии и многоугольники; графики функций в декартовых координатах; также графики в полярных координатах, контурные графики и изображения векторных полей. Некоторые примеры будут показаны ниже. Для более исчерпывающей информации по построению графиков см. Решение дифференциальных уравнений и Maxima, а также документацию Sage Constructions.

Данная команда построит желтую окружность радиуса 1 с центром в начале:

sage: circle((0,0), 1, rgbcolor=(1,1,0))
Graphics object consisting of 1 graphics primitive

Также можно построить круг:

sage: circle((0,0), 1, rgbcolor=(1,1,0), fill=True)
Graphics object consisting of 1 graphics primitive

Можно создавать окружность и задавать ее какой-либо переменной. Данный пример не будет строить окружность:

sage: c = circle((0,0), 1, rgbcolor=(1,1,0))

Чтобы построить ее, используйте c. 3),(x,0,2*pi),rgbcolor=hue(0.6)) sage: show(p1+p2+p3, axes=false)

Хороший способ создания заполненных фигур — создание списка точек (L в следующем примере), а затем использование команды polygon для построения фигуры с границами, образованными заданными точками. К примеру, создадим зеленый дельтоид:

sage: L = [[-1+cos(pi*i/100)*(1+cos(pi*i/100)),
....:     2*sin(pi*i/100)*(1-cos(pi*i/100))] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,3/4,1/2))
sage: p
Graphics object consisting of 1 graphics primitive

Напечатайте show(p, axes=false), чтобы не показывать осей на графике.

Можно добавить текст на график:

sage: L = [[6*cos(pi*i/100)+5*cos((6/2)*pi*i/100),
....:     6*sin(pi*i/100)-5*sin((6/2)*pi*i/100)] for i in range(200)]
sage: p = polygon(L, rgbcolor=(1/8,1/4,1/2))
sage: t = text("hypotrochoid", (5,4), rgbcolor=(1,0,0))
sage: show(p+t)

Учителя математики часто рисуют следующий график на доске: не одну ветвь arcsin, а несколько, т. е. график функции \(y=\sin(x)\) для \(x\) между \(-2\pi\) и \(2\pi\), перевернутый по отношению к линии в 45 градусов. Следующая команда Sage построит вышеуказанное:

sage: v = [(sin(x),x) for x in srange(-2*float(pi),2*float(pi),0.1)]
sage: line(v)
Graphics object consisting of 1 graphics primitive

Так как функция тангенса имеет больший интервал, чем синус, при использовании той же техники для перевертывания тангенса требуется изменить минимальное и максимальное значения координат для оси x:

sage: v = [(tan(x),x) for x in srange(-2*float(pi),2*float(pi),0.01)]
sage: show(line(v), xmin=-20, xmax=20)

Sage также может строить графики в полярных координатах, контурные построения и изображения векторных полей (для специальных видов функций). Далее следует пример контурного чертежа:

sage: f = lambda x,y: cos(x*y)
sage: contour_plot(f, (-4, 4), (-4, 4))
Graphics object consisting of 1 graphics primitive

Трехмерные графики

Sage также может быть использован для создания трехмерных графиков. 2 - 1) sage: implicit_plot3d(f, (x, -0.5, 0.5), (y, -1, 1), (z, -1, 1)) Graphics3d Object

примеры решения производных

Производная функции является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.

Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.

Таблица производных и правила дифференцирования

Основные ссылки - таблица производных, правила дифференцирования и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ.

Больше примеров решений →

Производные сложных функций

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание.Найти производную функции

Решение. По правилу дифференцирования сложной функции:

В свою очередь производная также берется по правилу дифференцирования сложной функции:

Ответ.

Больше примеров решений →

Применение дифференциала в приближенных вычислениях

Основные ссылки - теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Геометрический смысл производной

Основные ссылки - теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Механический смысл производной

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Точка движется по закону . Чему равна скорость в момент времени ?

Решение. Найдем скорость точки как первую производную от перемещения:

В момент времени скорость равна

Ответ.

Больше примеров решений →

Уравнение касательной, нормали и угол между прямыми

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Записать уравнение касательной к графику функции в точке

Решение. Найдем значение функции в заданной точке:

Найдем производную заданной функции по правилу дифференцирования произведения:

Вычислим её значение в заданной точке

Используя формулу

запишем уравнение касательной:

Ответ. Уравнение касательной:

Больше примеров решений →

Производные высших порядков

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную второго порядка от функции

Решение. Находим первую производную как производную сложной функции:

Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель - - есть сложной функцией:

Ответ.

Больше примеров решений →

Механическое смысл второй производной

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Уравнение движения материальной точки вдоль оси имеет вид (м). Найти ускорение точки в момент времени c.

Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:

Первая производная

(м/с)

вторая производная

(м/с²)

В момент времени c

(м/с²)

Ответ. (м/с²)

Больше примеров решений →

Дифференциалы высших порядков

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти дифференциал третьего порядка функции

Решение. По формуле

Найдем третью производную заданной функции:

Тогда

Ответ.

Больше примеров решений →

Производная функции, заданной неявно

Основные ссылки - теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Производная функции, заданной параметрически

Основные ссылки - теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Логарифмическое дифференцирование

Основные ссылки - теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Применим логарифмическое дифференцирование:

Тогда, продифференцировав левую и правую часть, будем иметь:

Отсюда получаем, что

Ответ.

Больше примеров решений →

Формулы Маклорена и Тейлора

Основные ссылки - теоретический материал и примеры решений (10 шт).

Больше примеров решений →

Вы поняли, как решать? Нет?

Помощь с решением

Калькулятор онлайн - Найти (с решением) производную функции

Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т. е. список формул для нахождения производных от некоторых элементарных функций.

Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.

Примеры подробного решения >>

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Определение производной

Определение. Пусть функция \( y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \( x_0 \). Дадим аргументу приращение \( \Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции \( \Delta y \) (при переходе от точки \( x_0 \) к точке \( x_0 + \Delta x \) ) и составим отношение \( \frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \( \Delta x \rightarrow 0 \), то указанный предел называют производной функции \( y=f(x) \) в точке \( x_0 \) и обозначают \( f'(x_0) \).

$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0) $$

Для обозначения производной часто используют символ \( y' \). Отметим, что \( y' = f(x) \) - это новая функция, но, естественно, связанная с функцией \( y = f(x) \), определенная во всех точках \(x\), в которых существует указанный выше предел. Эту функцию называют так: производная функции \( y = f(x) \).

Геометрический смысл производной состоит в следующем. Если к графику функции \( y = f(x) \) в точке с абсциссой \( x=a \) можно провести касательную, непараллельную оси \(y\), то \( f(a) \) выражает угловой коэффициент касательной:
\( k = f'(a) \)

Поскольку \( k = tg(a) \), то верно равенство \( f'(a) = tg(a) \) .

А теперь истолкуем определение производной с точки зрения приближенных равенств.2 \) справедливо приближенное равенство \( \Delta y \approx 2x \cdot \Delta x \). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.

Сформулируем его.

Как найти производную функции у = f(x) ?

1. Зафиксировать значение \( x \), найти \( f(x) \)
2. Дать аргументу \( x \) приращение \( \Delta x \), перейти в новую точку \( x+ \Delta x \), найти \( f(x+ \Delta x) \)
3. Найти приращение функции: \( \Delta y = f(x + \Delta x) - f(x) \)
4. Составить отношение \( \frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке \(x\).

Если функция \(y=f(x)\) имеет производную в точке \(x\), то ее называют дифференцируемой в точке \(x\). Процедуру нахождения производной функции \(y=f(x)\) называют дифференцированием функции \(y=f(x)\).

Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.

Пусть функция \(y=f(x)\) дифференцируема в точке \(x\). Тогда к графику функции в точке \( M(x; \; f(x)) \) можно провести касательную, причем, напомним, угловой коэффициент касательной равен \( f'(x) \). Такой график не может «разрываться» в точке \(M\), т. е. функция обязана быть непрерывной в точке \(x\).

Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция \(y=f(x)\) дифференцируема в точке \(x\), то выполняется приближенное равенство \( \Delta y \approx f'(x) \cdot \Delta x \). Если в этом равенстве \( \Delta x \) устремить к нулю, то и \( \Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.

Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.

Обратное утверждение неверно. Например: функция \( y=|x|\) непрерывна везде, в частности в точке \(x=0\), но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.

Еще один пример. Функция \( y=\sqrt[3]{x} \) непрерывна на всей числовой прямой, в том числе в точке \(x=0\). И касательная к графику функции существует в любой точке, в том числе в точке \(x=0\). Но в этой точке касательная совпадает с осью \(y\), т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид \(x=0\). Углового коэффициента у такой прямой нет, значит, не существует и \( f'(0) \)

Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?

Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.2} $$

Построить неявную функцию - MATLAB fimplicit

Цвет заливки маркера, заданный как 'auto' , триплет RGB, шестнадцатеричный цвет код, название цвета или короткое название. 'auto' значение использует то же color как свойство MarkerEdgeColor .

Для пользовательского цвета укажите триплет RGB или шестнадцатеричный цветовой код.

• Триплет RGB - это трехэлементный вектор-строка, элементы которого укажите интенсивность красного, зеленого и синего компоненты цвета.Интенсивности должны быть в диапазон [0,1] ; например, [0,4 0,6 0,7] .

• Шестнадцатеричный цветовой код - это вектор символов или строка. скаляр, который начинается с хеш-символа ( # ) за которыми следуют три или шесть шестнадцатеричных цифр, которые могут варьироваться с 0 до F .В значения не чувствительны к регистру. Таким образом, цветовые коды '# FF8800' , '# ff8800' , '# F80' и '# f80' эквивалентны.

Вы также можете указать некоторые общие цвета по имени. В этой таблице перечислены названные цвета параметры, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.

'w'

Название цвета	Краткое название	Триплет RGB	Шестнадцатеричный код цвета	Внешний вид
'красный'	'r'	[1 0 0]	'# FF0000'
'зеленый'	'g'	[0 1 0]	'# 00FF00'
'синий'	'b'	[0 0 1]	'# 0000FF'
'голубой	'c'	[0 1 1]	'# 00FFFF'
'пурпурный'	'm'	[1 0 1]	'# FF00FF'
'желтый'	'y'	[1 1 0]	'# FFFF0066
'черный'	'k'	[0 0 0]	'# 000000'
'белый66	[1 1 1]	'#FFFFFF'
'нет'	Неприменимо	Неприменимо	Неприменимо	N o цвет

Вот триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию, которые MATLAB использует во многих типах графиков.

4940 0,1840 0,5560]

Триплет RGB	Шестнадцатеричный цветовой код	Внешний вид
[0 0,4470 0,7410]	'# 0072BD'	2 0 [0,8500 0,3250 0,0980]	'# D95319'
[0,9290 0,6940 0,1250]	'# EDB120'		'# 7E2F8E'
[0,4660 0,6740 0,1880]	'# 77AC30'	1
'# 4DBEEE'
[0,6350 0,0780 0,1840]	'# A2142F'

Пример: [0. 3 .2 + х * у — 1

Эта функция будет успешно определена без бросания, но не будет построена, потому что она трехмерна. Вы можете построить только один двухмерный «срез» за раз:

  г (х) = f (х, 0)
  

Это будет участок.

Построение неявных функций в R

Так что, готовясь к моей последней рукописи по динамике населения, я создал все необходимые цифры. Один из них, который я рассмотрел, был двумерным поверхностным графиком модифицированного уравнения Рикера, показывающим переходы от устойчивости к экстинкции и устойчивости к предельным циклам.2} \] Итак, если у вас есть неявная функция, которую вы хотите построить, как вы могли бы сделать это в R? Простой ответ — численно решить уравнение в определенном диапазоне, но как тогда его построить?

 my.fun 
 В результате будет получен график, похожий на рисунок слева, тогда как рисунок справа был создан с помощью написанной мной функции под названием imp.solve (). 
 
 my.fun В первом примере создается быстрый и грязный график, который хорош и хорош, но это поверхностный график. Это означает, что вы застряли с «0» на линии, обозначающей, что поверхность - это только области рисования, где 0.Вдобавок вы теряете и другой контроль над тем, что вы можете рисовать и что, если вы хотите использовать ggplot2 или какой-то другой пакет, или вы действительно хотите знать, каков числовой ответ? Моя функция анализирует 
 вывод функции external () и возвращает фрейм данных, который вы можете легко построить в ggplot2. Он может обрабатывать большинство полиномиальных функций, хотя я оставлю вас ответственным за упорядочивание собственного вывода для линейных графиков в сценариях с несколькими x в одной и той же точке y. Вот еще один пример с кубической функцией.{(\ gamma - r)} - \ gamma = 0 \] Если оставить константу c равной 0,01, следующий код сгенерирует нашу фигуру. 
 ########## Сначала настройте параметры для изменения ########
y Это то же самое, что и первая строка на приведенном выше рисунке из бумаги. Вы можете найти полный код этой функции на моей странице github как Imp.solve.R. Итак, хотя ранее в R существовало быстрое и грязное решение, вот улучшенная версия с большей гибкостью построения графиков. Удачного построения графиков неявных функций! 
 

Исчисление I — неявное дифференцирование

Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-10: Неявная дифференциация

К этому моменту мы сделали довольно много производных, но все они были производными функций вида \ (y = f \ left (x \ right) \).К сожалению, не все функции, которые мы собираемся рассмотреть, попадут в эту форму.

Давайте взглянем на пример такой функции.

Пример 1 Найдите \ (y ‘\) для \ (xy = 1 \). Показать решение

На самом деле есть два метода решения этой проблемы.

Решение 1:

Это простой способ решить проблему. Просто решите для \ (y \), чтобы получить функцию в форме, с которой мы привыкли иметь дело, а затем дифференцируйте.2}}} \]

Итак, это сделать достаточно просто. Однако есть некоторые функции, для которых это невозможно. Вот где в игру вступает второй метод решения.

Решение 2:

В этом случае мы собираемся оставить функцию в той форме, которую нам дали, и работать с ней в этой форме. Однако давайте вспомним из первой части этого решения, что если бы мы могли решить для \ (y \), то мы получили бы \ (y \) как функцию от \ (x \).Другими словами, если бы мы могли решить для \ (y \) (как мы могли бы в этом случае, но не всегда сможем это сделать), мы получим \ (y = y \ left (x \ right) \). Давайте перепишем уравнение, чтобы это отметить.

\ [xy = x \, y \ left (x \ right) = 1 \]

Будьте осторожны и заметьте, что когда мы пишем \ (y \ left (x \ right) \), мы не имеем в виду \ (y \) раз \ (x \). Здесь мы отмечаем, что \ (y \) является некоторой (возможно, неизвестной) функцией от \ (x \). Об этом важно помнить при выполнении этой техники решения проблем.

Следующим шагом в этом решении является дифференцирование обеих сторон относительно \ (x \) следующим образом:

\ [\ frac {d} {{dx}} \ left ({x \, y \ left (x \ right)} \ right) = \ frac {d} {{dx}} \ left (1 \ right) \ ]

Правая сторона легкая. Это просто производная от константы. Левая сторона также проста, но мы должны признать, что у нас действительно есть продукт, \ (x \) и \ (y \ left (x \ right) \). Итак, чтобы произвести производную от левой части, нам нужно выполнить правило продукта.Это дает

\ [\ left (1 \ right) y \ left (x \ right) + x \ frac {d} {{dx}} \ left ({y \ left (x \ right)} \ right) = 0 \]

Теперь напомним, что у нас есть следующий способ записи производной.

\ [\ frac {d} {{dx}} \ left ({y \ left (x \ right)} \ right) = \ frac {{dy}} {{dx}} = y ‘\]

Используя это, мы получаем следующее:

\ [у + ху ‘= 0 \]

Обратите внимание, что мы уронили \ (\ left (x \ right) \) на \ (y \), поскольку он был там только для того, чтобы напомнить нам, что \ (y \) был функцией \ (x \), и теперь что мы взяли производную, она больше не нужна.Мы просто хотели, чтобы в уравнении распознавалось правило продукта, когда мы берем производную.

Итак, давайте теперь вспомним, что нам было нужно. Мы искали производную \ (y ‘\) и заметили, что теперь в уравнении есть \ (y’ \). Итак, чтобы получить производную, все, что нам нужно сделать, это решить уравнение для \ (y ‘\).

\ [y ‘= — \ frac {y} {x} \]

Вот оно. Это наш ответ, используя второй метод решения.{2}}} \]

, что мы и получили от первого решения. Независимо от используемой техники решения мы должны получить одну и ту же производную.

Процесс, который мы использовали во втором решении предыдущего примера, называется неявным дифференцированием и является предметом этого раздела. В предыдущем примере мы смогли просто решить для \ (y \) и избежать неявного дифференцирования. Однако в остальных примерах этого раздела мы либо не сможем решить для \ (y \), либо, как мы увидим в одном из примеров ниже, ответ не будет в той форме, в которой мы могу разобраться.

Во втором решении выше мы заменили \ (y \) на \ (y \ left (x \ right) \), а затем сделали производную. Напомним, мы сделали это, чтобы напомнить нам, что \ (y \) на самом деле является функцией \ (x \). Мы будем делать это довольно часто в этих задачах, хотя на самом деле мы редко пишем \ (y \ left (x \ right) \). Итак, прежде чем мы фактически займемся проблемами неявного дифференцирования, давайте сделаем быстрый набор «простых» производных, которые, мы надеемся, помогут нам в создании производных функций, которые также содержат \ (y \ left (x \ right) \).{у \ влево (х \ вправо)}} \) Показать все решения Скрыть все решения

Они написаны немного иначе, чем мы привыкли здесь видеть. Это потому, что мы хотим сопоставить эти проблемы с тем, что мы будем делать в этом разделе. Кроме того, каждая из этих частей имеет несколько функций, которые нужно различать, начиная с конкретной функции, за которой следует общая функция. Это опять же, чтобы помочь нам с некоторыми конкретными частями процесса неявной дифференциации, который мы будем делать.2} — 7} \ right) \]

и это всего лишь цепное правило. Мы дифференцировали внешнюю функцию (показатель степени 5), а затем умножили это на производную внутренней функции (материал внутри скобок).

Для второй функции мы сделаем в основном то же самое. Нам нужно будет использовать цепное правило. Внешняя функция по-прежнему имеет показатель степени 5, а внутренняя функция на этот раз просто \ (f \ left (x \ right) \). У нас нет здесь конкретной функции, но это не значит, что мы не можем, по крайней мере, записать цепное правило для этой функции.4} е ‘\ влево (х \ вправо) \]

На самом деле мы не знаем, что такое \ (f \ left (x \ right) \), поэтому, когда мы делаем производную внутренней функции, все, что мы можем сделать, это записать обозначение для производной, , т.е. \ (f ‘ \ влево (х \ вправо) \).

В последней функции мы просто заменили \ (f \) во второй функции на \ (y \), поскольку большая часть нашей работы в этом разделе будет включать \ (y \) вместо \ (f \). с. В остальном эта функция идентична второй.4} у ‘\ влево (х \ вправо) \]
b \ (\ sin \ left ({3 — 6x} \ right) \), \ (\ sin \ left ({y \ left (x \ right)} \ right) \) Показать решение

Первая функция, которую нужно дифференцировать здесь, — это снова проблема с правилом быстрой цепочки, так что вот ее производная,

\ [\ frac {d} {{dx}} \ left [{\ sin \ left ({3 — 6x} \ right)} \ right] = — 6 \ cos \ left ({3 — 6x} \ right) \ ]

Для второй функции на этот раз мы не стали использовать \ (f \ left (x \ right) \) и просто перешли прямо к \ (y \ left (x \ right) \) для общей версии.Это пока всего лишь общая версия того, что мы сделали для первой функции. Внешняя функция по-прежнему является синусом, а внутренняя задается как \ (y \ left (x \ right) \), и хотя у нас нет формулы для \ (y \ left (x \ right) \), поэтому мы на самом деле не может взять его производную, у нас есть обозначение для ее производной. Вот производная для этой функции,

\ [\ frac {d} {{dx}} \ left [{\ sin \ left ({y \ left (x \ right)} \ right)} \ right] = y ‘\ left (x \ right) \ cos \ left ({y \ left (x \ right)} \ right) \]
c \ ({{\ bf {e}} ^ {{x ^ 2} — 9x}} \), \ ({{\ bf {e}} ^ {y \ left (x \ right)}} \) Показать решение

В этой части мы просто дадим ответы по каждому из них и опустим объяснение, которое у нас было в первых двух частях.{у \ влево (х \ вправо)}} \]

Итак, в этом наборе примеров мы просто решали некоторые задачи с цепными правилами, где внутренняя функция была \ (y \ left (x \ right) \) вместо конкретной функции. Этот вид производной постоянно проявляется при неявном дифференцировании, поэтому нам нужно убедиться, что мы можем их выполнять. Также обратите внимание, что мы сделали это только для трех типов функций, но есть гораздо больше видов функций, которые мы могли бы использовать здесь.

Итак, пришло время решить нашу первую задачу, где требуется неявное дифференцирование, в отличие от первого примера, где мы могли бы фактически избежать неявного дифференцирования, решая для \ (y \).2}} \]

Перед тем, как приступить к этой задаче, мы заявили, что здесь нам нужно выполнить неявное дифференцирование, потому что мы не можем просто решить для \ (y \), и тем не менее это то, что мы только что сделали. Итак, почему мы не можем использовать здесь «нормальную» дифференциацию? Проблема в «\ (\ pm \)». Имея это в «решении» для \ (y \), мы видим, что \ (y \) на самом деле две разные функции. Что мы должны использовать? Стоит ли использовать и то, и другое? Нам нужна только одна функция для производной, и в лучшем случае у нас есть две функции.1} y ‘\ left (x \ right) = 0 \]

На этом этапе мы можем отбросить часть \ (\ left (x \ right) \), поскольку это было только в задаче, чтобы помочь с процессом дифференцирования. Последний шаг — просто решить полученное уравнение для \ (y ‘\).

\ [\ begin {align *} 2x + 2yy ‘& = 0 \\ y’ & = — \ frac {x} {y} \ end {align *} \]

В отличие от первого примера, мы не можем просто подключить \ (y \), так как мы не знаем, какую из двух функций использовать.2} = 9 \]

в точке \ (\ left ({2, \, \, \ sqrt 5} \ right) \).

Показать решение

Во-первых, обратите внимание, что в отличие от всех других задач касательной, которые мы решали в предыдущих разделах, нам нужно задавать значения как \ (x \), так и \ (y \) точки. Также обратите внимание, что эта точка действительно лежит на графике окружности (вы можете проверить, подставив точки в уравнение), поэтому в этой точке можно говорить о касательной.

Напомним, что для записи касательной все, что нам нужно, — это наклон касательной, и это не что иное, как производная, вычисленная в данной точке.У нас есть производная от предыдущего примера, поэтому все, что нам нужно сделать, это подключить данную точку.

\ [m = {\ left. {y ‘} \ right | _ {x = 2, \, y = \ sqrt 5}} = — \ frac {2} {{\ sqrt 5}} \]

Тогда касательная прямая.

\ [y = \ sqrt 5 — \ frac {2} {{\ sqrt 5}} \ left ({x — 2} \ right) \]

А теперь давайте поработаем еще несколько примеров. В остальных примерах мы больше не будем писать \ (y \ left (x \ right) \) вместо \ (y \).Это просто то, что мы делали, чтобы напомнить себе, что \ (y \) на самом деле является функцией \ (x \), чтобы помочь с производными. Увидев \ (y \ left (x \ right) \), мы напомнили нам, что нам нужно применить цепное правило для этой части проблемы. С этого момента мы оставим \ (y \) записанными как \ (y \), и в нашей голове нам нужно будет помнить, что они на самом деле \ (y \ left (x \ right) \ ) и что нам нужно выполнить цепное правило.

Есть простой способ запомнить, как применять цепное правило в этих задачах.Цепное правило действительно говорит нам дифференцировать функцию, как мы обычно это делали бы, за исключением того, что нам нужно добавить производную от внутренней функции. При неявном дифференцировании это означает, что каждый раз, когда мы дифференцируем терм с \ (y \) в нем, внутренняя функция — это \ (y \), и нам нужно будет добавить \ (y ‘\) к члену, поскольку это будет — производная внутренней функции.

Давайте посмотрим на пару примеров.

Пример 5 Найдите \ (y ‘\) для каждого из следующих значений.3} + 1 \) Показать решение

Сначала дифференцируйте обе части относительно \ (x \) и помните, что каждый \ (y \) на самом деле \ (y \ left (x \ right) \), мы просто больше не собираемся писать его таким образом. Это означает, что первый член слева будет правилом продукта.

Мы разграничили эти виды функций, включающих \ (y \) ’, в степень с помощью цепного правила в примере 2 выше. Также вспомните обсуждение этой проблемы до начала. При решении такой задачи цепного правила все, что нам нужно сделать, это дифференцировать \ (y \) как нормальные, а затем добавить \ (y ‘\), который является не чем иным, как производной от «внутренней функции ».2} г ‘\]

Теперь все, что нам нужно сделать, это найти производную \ (y ‘\). Это просто базовая решающая алгебра, которую вы можете делать. Основная проблема в том, что это может быть более беспорядочным, чем то, к чему вы привыкли. Все, что нам нужно сделать, это получить все члены с \ (y ‘\) в них с одной стороны и все термины без \ (y’ \) с другой. Затем вычлените \ (y ‘\) из всех членов, содержащих его, и разделите обе части на «коэффициент» \ (y’ \). Вот решение для этого,

\ [\ begin {align *} 3 {x ^ 2} {y ^ 5} + 3 & = 24 {y ^ 2} y ‘- 5 {x ^ 3} {y ^ 4} y’ \\ 3 {x ^ 2} {y ^ 5} + 3 & = \ left ({24 {y ^ 2} — 5 {x ^ 3} {y ^ 4}} \ right) y ‘\\ y’ & = \ frac {{ 3 {x ^ 2} {y ^ 5} + 3}} {{24 {y ^ 2} — 5 {x ^ 3} {y ^ 4}}} \ end {align *} \]

Алгебра в этих задачах может быть довольно запутанной, так что будьте осторожны.3}} \ right) \) Показать решение

С этой проблемой нужно быть осторожнее. У нас есть пара правил цепочки, с которыми нам придется иметь дело здесь, которые немного отличаются от тех, с которыми мы имели дело до этой проблемы.

И в экспоненте, и в логарифме у нас есть «стандартное» цепное правило, заключающееся в том, что внутри экспоненты и логарифма есть нечто иное, чем просто \ (x \) или \ (y \). Итак, это означает, что здесь мы будем применять правило цепочки, как обычно, а затем, когда мы будем выполнять производную внутренней функции для каждого члена, нам придется иметь дело с дифференцированием \ (y \) ‘s.{- 1}}}} \ end {align *} \]

Обратите внимание, что для того, чтобы производная хотя бы выглядела немного лучше, мы преобразовали все дроби в отрицательные показатели.

Хорошо, мы видели одно применение неявного дифференцирования в приведенном выше примере касательной. Однако есть еще одно приложение, которое мы увидим в каждой проблеме в следующем разделе.

В некоторых случаях у нас будет две (или более) функции, каждая из которых является функциями третьей переменной.Итак, у нас могут быть \ (x \ left (t \ right) \) и \ (y \ left (t \ right) \), например, и в этих случаях мы будем дифференцировать по \ (t \) . Это просто неявное дифференцирование, как мы делали в предыдущих примерах, но есть разница.

В предыдущих примерах у нас есть функции, включающие \ (x \) ’s и \ (y \)’ s, и считающие \ (y \) как \ (y \ left (x \ right) \). В этих задачах мы производили дифференцирование по отношению к \ (x \), и поэтому, столкнувшись с \ (x \) в функции, которую мы дифференцировали как нормальную, и когда мы столкнулись с \ (y \), мы дифференцировались как нормальные, кроме добавили \ (y ‘\) к этому термину, потому что мы действительно применяли цепное правило.

В новом примере, который мы хотим рассмотреть, мы предполагаем, что \ (x = x \ left (t \ right) \) и что \ (y = y \ left (t \ right) \) и производим дифференцирование по \ (т \). Это означает, что каждый раз, когда мы сталкиваемся с \ (x \) или \ (y \), мы будем выполнять цепное правило. Это, в свою очередь, означает, что когда мы дифференцируем \ (x \), нам нужно будет добавить \ (x ‘\), и всякий раз, когда мы дифференцируем \ (y \), мы будем добавлять \ (y’ \).

Эти новые типы проблем на самом деле аналогичны задачам, которые мы обсуждали в этом разделе.{1 — x}} + 5y ‘\ sin \ left ({5y} \ right) = 2yy’ \]

В этой проблеме действительно не так уж и много. Поскольку в задаче есть две производные, мы не будем пытаться решить одну из них. Когда мы решаем такую ​​задачу в следующем разделе, проблема будет подразумевать, какую из них нам нужно решить.

На данный момент, похоже, нет реальной причины для решения такого рода задач, но, как мы увидим в следующем разделе, каждая задача, которую мы будем там решать, будет включать в себя такого рода неявную дифференциацию.

Калькулятор неявной функции

Многомерное исчисление; Осень 2013 г. С. Джамшиди получит dz dt = 80t3 sin 20t4 +1 t + 1 t2 sin 20t4 +1 t Пример 5.6.0.4 2. Программное обеспечение для набора текста Glencoe, ответы на домашние задания по саксонской математике, математика в средней школе с Pizzazz! Оценка W (x) Поскольку функция, обратная функции f (x) = xe x, не может быть выражена в терминах элементарных функций, аналитики используют численные алгоритмы для оценки функции W Ламберта при значении x. Калькулятор асимптот бесплатных функций — пошаговый поиск вертикальных и горизонтальных асимптот функций. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Ваш браузер не поддерживает холст HTML5. Предположим, что все эти функции определены в некотором шаре, поэтому они непрерывно дифференцируемы, есть шар. Дифференциальный калькулятор — это онлайн-инструмент исчисления, который находит производную заданной функции. Предположим, что … Нас просят найти … Он использует те же шаги, что и стандартные вычисления на бумаге и карандаше, но намного быстрее, чем на это способен человек. Например, неявное уравнение единичной окружности: x2 + y2 — 1 = 0. В этом видео показано, что нужно помнить о неявном дифференцировании, а затем найти одну частную производную.Неявное дифференцирование может помочь нам решить обратные функции. Неявное дифференцирование — это метод, который использует цепное правило для дифференцирования неявно определенных функций. Продолжить чтение Производная неявной функции многих переменных — Вычисление частных производных уравнения с экспонентой — Упражнение 6481. Какова неявная скорость в ASC 842? Неявные функции. Определение неявных функций. До сих пор в этом курсе мы говорили только о функциях, которые присваивают каждому действительному числу x в своем домене ровно одно действительное число f (x).Графики функции f (x) — это набор всех точек (x; y), таких что y = f (x), и мы обычно визуально график функции в виде кривой, для которой каждая вертикальная линия пересекает y, является зависимая переменная и выражается через независимую переменную x. Калькулятор неявной производной — это простой онлайн-инструмент, который может легко найти неявную производную любой заданной функции. Неявная функция — это функция, которая неявно определяется неявным уравнением путем связывания одной из переменных (значения) с другими (аргументами).2, y = sin (x), y = 1 / x и т. Д. Как вычислить интеграл с неявной функцией? Производная неявной функции многих переменных — Вычисление производной функции одной переменной — Упражнение 6476. Автор Laura Это пример более сложной задачи неявного дифференцирования. Неявная функция Scala. Тест по математике для 11 класса, «Проект математической школы Чикагского университета: алгебра», калькулятор неявного дифференцирования geocities, бесплатные онлайн-калькуляторы трехчлена факторинга. ШАГ ЗА ШАГОМ Неявная дифференциация с примерами — узнайте, как это сделать, за 4 шага или всего за 1 шаг.Определим функцию парой параметрических уравнений: и. Явная функция — это функция, которая задается в терминах. Калькулятор средней разницы для любой комбинации int Теперь вернемся к этой теореме о неявной функции номер три. ∫ 0 1 е (я г) д я. где f (iz) имеет вид: f (i z) = ∫ 0,3 0,9 g (i x) d x. а g (ix) выглядит примерно так: g (i x) = exp i x ∗ z. Я хочу рассчитать это численно. Не каждую функцию можно явно записать в терминах независимой переменной e.г. Таким образом, x 2 + y 2 = 25, y 2 = 25 — x 2, неявное умножение (5x = 5 * x) поддерживается. Приведенный выше калькулятор находит значение вашего производного ордера, используя процесс, известный как неявное дифференцирование. Найдите больше виджетов математики в Wolfram | Alpha. Я пытаюсь вычислить неявную производную следующей функции с целью проверить, когда она положительна, а когда отрицательна. Подписаться 46 просмотров (за последние 30 дней) Показать старые комментарии. Например, y = 3x + 1 является явным, где y является зависимой переменной и зависит от независимой переменной x.2y = x + 3y Зарегистрировавшись, вы получите тысячи пошаговых решений для ваших домашних заданий. Используйте этот удобный бесплатный онлайн-калькулятор неявной дифференциации, чтобы получить точный вывод уравнения за доли секунды. 3 = 8.Ответил: Chidvi Modala 30 августа 2019 г. Привет, ereryone, у меня вопрос для интеграла. Калькулятор найдет касательную к явной, полярной, параметрической и неявной кривой в заданной точке с указанными шагами. Явная функция — это функция, которая задается в терминах независимой переменной. Нахождение области определения функции алгебраически без графа Неявное дифференцирование функции многих переменных Пример 1 Неявное дифференцирование функции многих переменных Пример 2. Неявное дифференцирование: Отправить: Вычисления… Получите этот виджет. У нас есть функция f (x, y), где y (x), и мы знаем, что dy dx = — fx fy. Используя этот сайт, вы соглашаетесь с нашей Политикой в ​​отношении файлов cookie. — Мой совет: держитесь подальше от чистых неявных преобразований, они опасны, используйте вместо них методы расширения. Он может выполнять как явное, так и неявное дифференцирование одним щелчком мыши. Выберите «Найти производную» в меню и щелкните, чтобы увидеть результат! lei yang 26 августа 2019 г. Проверка рассчитанной неявной ставки. Поскольку уравнение имеет общий вид f (t, y, y ′) = 0, вы можете использовать функцию ode15i для решения неявного дифференциального уравнения.Вторая производная (f ») — это производная производной (f‘). Другими словами, чтобы найти вторую производную, возьмите производную дважды. Одна из причин найти вторую производную — найти ускорение по функции положения; первая производная от положения — это скорость, а вторая производная от положения — это ускорение. Выберите точку (x 0, y 0) так, чтобы f (x 0, y 0) = 0, но x 0 6 = 1, −1. Войдите или зарегистрируйтесь. Определите скрытые проценты по аренде. Неявная функция — это функция, записанная в терминах как зависимых, так и независимых переменных, например y-3x 2 + 2x + 5 = 0.Введите любую производную функции, чтобы получить решение, шаги и график. Это здорово! И я пытаюсь добраться до y ″, что согласно книге y ″ = — f2yfxx + 2fxfyfxy — f2xfyy f3y. Это здорово! Вы также можете лучше визуализировать и лучше понять функцию, используя наш инструмент построения графиков. Мы встречаемся со многими уравнениями, в которых y явно не выражается только через x, например:. Инструмент построения графиков неявных функций «Стандартное» программное обеспечение для построения графиков, такое как обычный калькулятор графиков, будет отображать только явные функции, то есть функции вида y = f (x), такие как y = x 2 — 2x + 1 или y = sin x, но не будет графически отображать неявные функции, такие как x 2 + xy — 2y 2 = 6 или x = sin y.dy a) Найдите dx b) Найдите уравнение касательной к кривой в точке (1,2). Неявная функция — это функция, в которой зависимая переменная не определяется в терминах независимых переменных или констант. Получите бесплатный виджет «Неявный плоттер» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Неявное дифференцирование — это процесс поиска производной функции без разделения переменных. Онлайн-калькулятор неявного дифференцирования поможет вам определить неявную производную заданных функций по переменной.Программное обеспечение калькулятора неявных функций Implicit Curves Rev v.3.1 Простой инструмент, который будет рисовать сложные функциональные кривые. Обычно кривые строятся по ЯВНОЙ формуле, такой как y = sin (x), где y находится на одной стороне знака равенства, и все, что связано с x, находится на другой стороне. Возьмем следующую функцию y = x 2 + 3x — 8. Калькулятор неявной дифференциации. Мы могли бы немедленно выполнить неявное дифференцирование снова, или мы могли бы решить для y и снова дифференцировать. присваивание делает z непрерывной функцией от x и y.Говоря простым языком, результат теоремы о неявной функции состоит в том, что для достаточно хороших точек на поверхности мы можем (локально) притвориться, что эта поверхность является графиком функции. Онлайн-калькулятор одновременных уравнений, рабочие листы таблиц функций, задачи со словами, интерактивная книга по алгебре, масштабный коэффициент по математике для 6-го класса, программа для определения, является ли указанная пользователем строка палиндромом в программировании на C. Онлайн-калькулятор параметрической производной. {2} -1 = 0}.Не знаете, что это значит? Резюме. Примечание. Калькулятор отображает значения x через y, что упрощает решение системы с помощью построения графиков. Самое главное, что калькулятор дифференциации показывает пошаговый расчет вместе с подробным ответом. Оси формата: Теорема о неявной функции позволяет нам (частично) свести невозможные вопросы о системах нелинейных уравнений к прямым вопросам о системах линейных уравнений. Исчисление с несколькими переменными — Теорема о неявной функции Как найти частные производные от неявно определенной функции с несколькими переменными с помощью теоремы о неявной функции? Некоторые отношения не могут быть представлены явной функцией.Калькулятор производных… Калькулятор производных Этот простой и удобный калькулятор производных поможет вам решить любую задачу, просто введите значение функции и вы сразу получите решение с подробным пошаговым описанием. График параметрической функции. независимая переменная. Использовал функцию перед определением сигнатуры функции или непосредственно в верхней части кода. {3} {\ left (x \ right)} \ right) = \ frac {d} {dx} \ left (2 xy {\ left (x \ right )} \ right) $$$.{2} {\ left (x \ right)} \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) \ right) $$$.

Продифференцируйте правую часть уравнения.

Примените правило кратных констант $$$ \ frac {d} {dx} \ left (cf {\ left (x \ right)} \ right) = c \ frac {d} {dx} \ left (f { \ left (x \ right)} \ right) $$$ с $$$ c = 2 $$$ и $$$ f {\ left (x \ right)} = xy {\ left (x \ right)} $ $$:

$$ \ color {красный} {\ left (\ frac {d} {dx} \ left (2 xy {\ left (x \ right)} \ right) \ right)} = \ color {красный } {\ left (2 \ frac {d} {dx} \ left (xy {\ left (x \ right)} \ right) \ right)} $$

Примените правило продукта $$$ \ frac {d} {dx} \ left (f {\ left (x \ right)} g {\ left (x \ right)} \ right) = \ frac {d} {dx} \ left (f {\ left (x \ right) } \ right) g {\ left (x \ right)} + f {\ left (x \ right)} \ frac {d} {dx} \ left (g {\ left (x \ right)} \ right) $ $$ с $$$ f {\ left (x \ right)} = x $$$ и $$$ g {\ left (x \ right)} = y {\ left (x \ right)} $$$:

$$ 2 \ color {red} {\ left (\ frac {d} {dx} \ left (xy {\ left (x \ right)} \ right) \ right)} = 2 \ color {red} {\ left (\ frac {d} {dx} \ left (x \ right) y {\ left (x \ right)} + x \ frac {d} {dx} \ left (y {\ left (x \ right)}) \ right) \ right)} $$

Примените правило мощности $$$ \ frac {d} {dx} \ left (x ^ {n} \ rig ht) = nx ^ {n — 1} $$$ с $$$ n = 1 $$$, другими словами, $$$ \ frac {d} {dx} \ left (x \ right) = 1 $$ $:

$$ 2 x \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) + 2 y {\ left (x \ right)} \ color {red} {\ left (\ frac {d} {dx} \ left (x \ right) \ right)} = 2 x \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) + 2 y {\ left (x \ right)} \ color {red} {\ left (1 \ right)} $$

Упростить:

$$ 2 x \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) + 2 y {\ left (x \ right)} = 2 \ left (x \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) + y {\ left (x \ right)} \ right) $$

Таким образом, $$$ \ frac {d} {dx} \ left (2 xy {\ left (x \ right)} \ right) = 2 \ left (x \ frac {d} {dx} \ left (y {\ left (x \ right)} \ right) + y {\ left (x \ right)} \ right) $$$.{2}} $$$.

8. Дифференциация неявных функций

М. Борна

Мы встречаем много уравнений, в которых y не выражаются явно только в терминах x , например:

f ( x , y ) = y ⁴ + 2 x ² y ² + 6 x ² = 7

Вы можете увидеть несколько примеров таких выражений в разделе «Полярные графики».

Обычно трудно, а то и невозможно решите относительно y так, чтобы затем мы могли найти `(dy) / (dx)`.

Нам нужно найти производные от таких выражения, чтобы найти скорость изменения y как x изменений. Для этого нам нужно знать неявных Дифференциация .

Давайте узнаем, как это работает, на некоторых примерах.

Пример 1

Начнем с неявной функции y ⁴ + x ⁵ -7 x ² -5 x ^-1 = 0.

Вот график этой неявной функции. Наблюдать:

1. Это необычная функция, потому что для каждого значения x (для регионов `x
2. Кривая имеет два «плеча»
3. Кривая вертикальна около `x = -1` и` x = 2`

Найдите производную этой неявной функции и выразите ответ в виде `dy / dx.`

Ответ

y ⁴ + x ⁵ -7 x ² -5 x ^-1 = 0

Мы видим, как выводить это выражение по частям.Мы просто получайте выражения по мере того, как мы подходим к ним слева направо верно.

(В этом примере мы могли бы легко выразить функцию только в терминах y , но это задуман как относительно простой первый пример.)

Часть A: Найдите производную по x из: y ⁴

Чтобы дифференцировать это выражение, мы рассматриваем y как функция x и используйте правило мощности.3`

Пример 2

Найдите наклон касательной в точке `(2, -1)` для кривой:

2 y + 5- x ² — y ³ = 0.

Ответ

Работаем слева направо, получаем:

Производная от 2y:

`d / (dx) 2y = 2 (dy) / (dx)`

Производная от 5 равна 0.

Производная от x ² — это `2x`.3 = 0`

и изобразите касательную к кривой в точке `(2, -1)`. Мы видим, что действительно наклон равен «-4».

Работает!

Пример 3 (включает правило продукта)

Найдите выражение для `(dy) / (dx)` если:

y ⁴ + 2 x ² y ² + 6 x ² = 7

(Это пример в верхней части этой страницы.)

Ответ

Во-первых, давайте изобразим неявную функцию, указанную в вопросе, чтобы увидеть, с чем мы работаем.