Нажмите "Enter", чтобы перейти к содержанию

График координаты: Графики зависимости перемещения и координаты тела от времени при движении с постоянным ускорением — урок. Физика, 9 класс.

Содержание

Графики равномерного, равноускоренного, равнозамедленного движения

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

  • движение без ускорения (равномерное), и
  • движение с ускорением (неравномерное).

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: \(\vec{a} =0\).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: \(\vec{a} =const\). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

  • Равноускоренное движение — скорость тела увеличивается.
  • Равнозамедленное движение — скорость уменьшается.

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

  • по горизонтали — время в секундах.
  • по вертикали — координаты тела, или проекции скорости и ускорения.

Для каждого вида движения получим три графика. Графики будем называть так:

  1. x(t) – зависимость координаты от времени;
  2. v(t) – зависимость проекции скорости от времени;
  3. a(t) – зависимость проекции ускорения от времени.

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой \(x_{0}\) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис.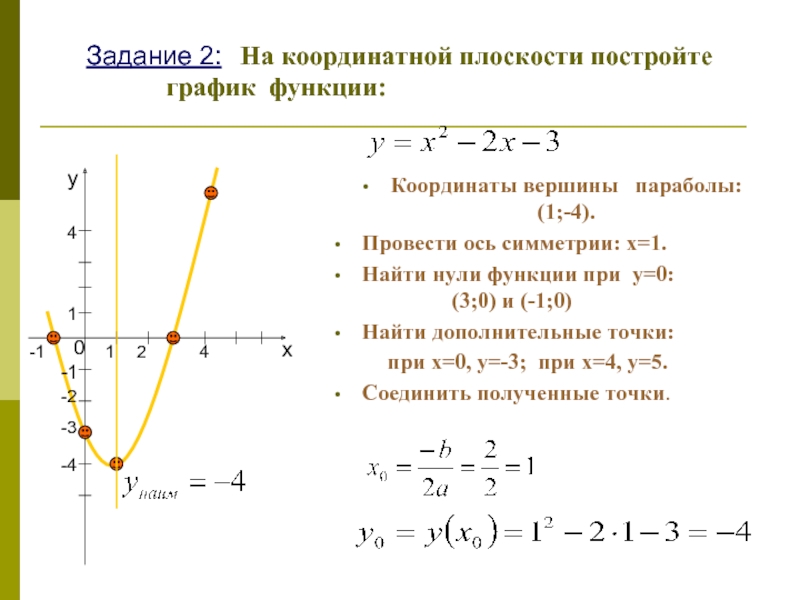 1б).
\[x=x_{0}\]

Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)

Скорость и ускорение неподвижного тела равны нулю:

\[\vec{v}=0\]

\[\vec{a}=0\]

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка \(x_{0}\), а конечная координата — точка \(x\) на  оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

 Примечание: Тело движется туда, куда направлен вектор его скорости.

Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

\[ x  = x_{0} + v \cdot t \]

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

\[ v  = v_{0} = const \]

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

\[ a = 0 \]

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Рис.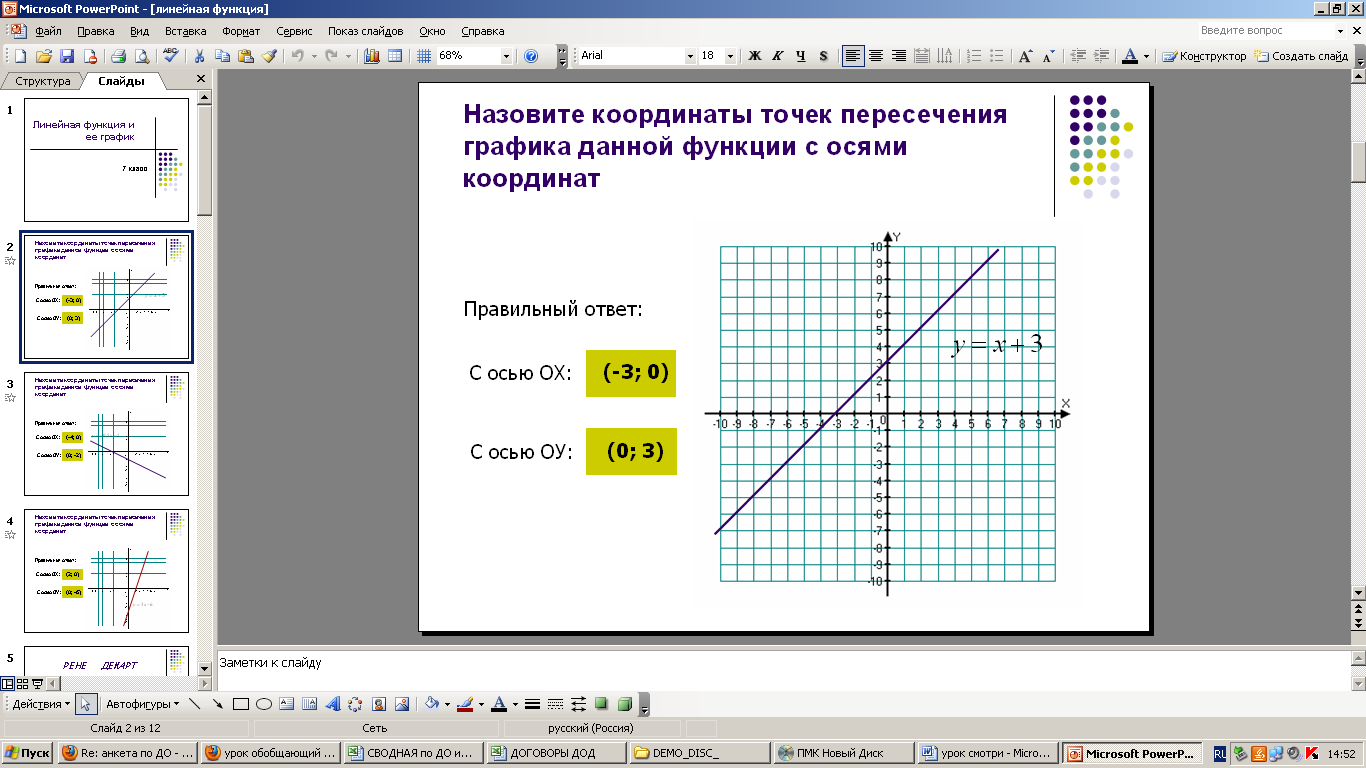 3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

{2} + v_{0} \cdot t + x_{0} \]

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

\[ v  = v_{0} + a \cdot t \]

Ускорение есть (рис. 4г) и оно не меняется:

\[ a = const \]

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

  • по линейному закону, когда скорость не меняется — остается одной и той же.
  • по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.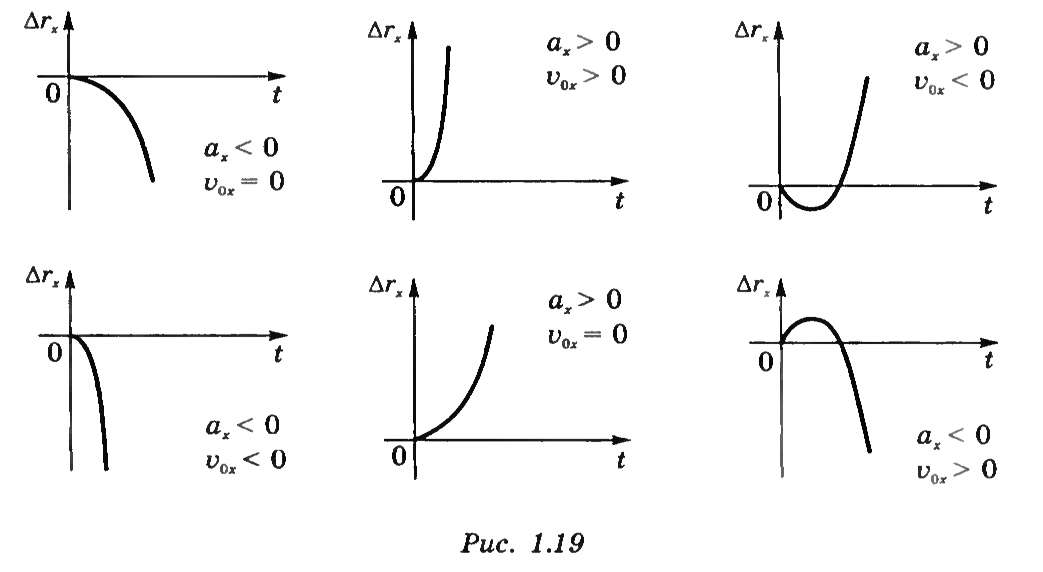

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов \(\vec{v}\) и \(\vec{a}\) на ось Ox будут отрицательными.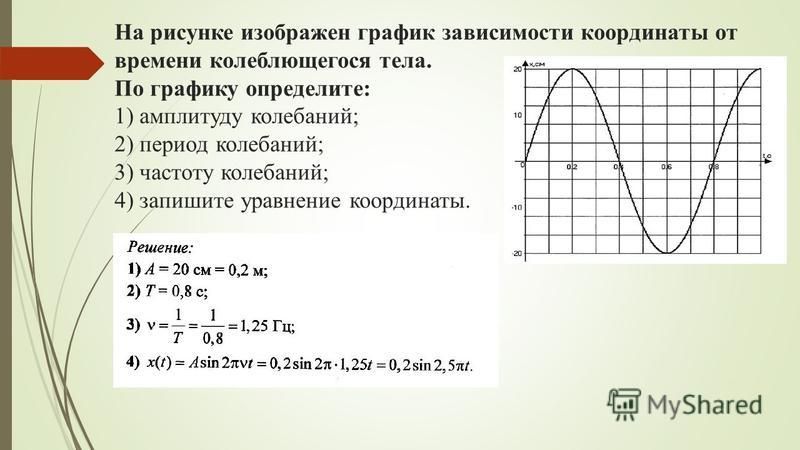 Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).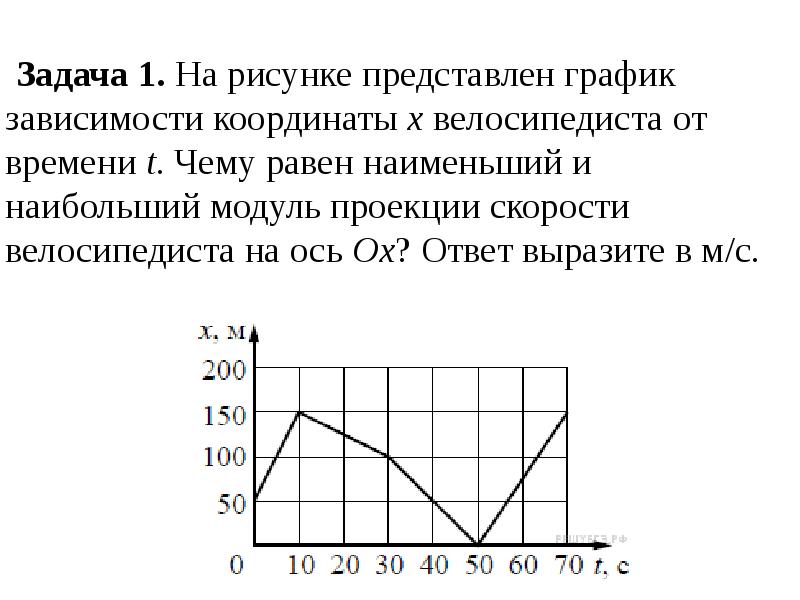

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени

Скорость отрицательная.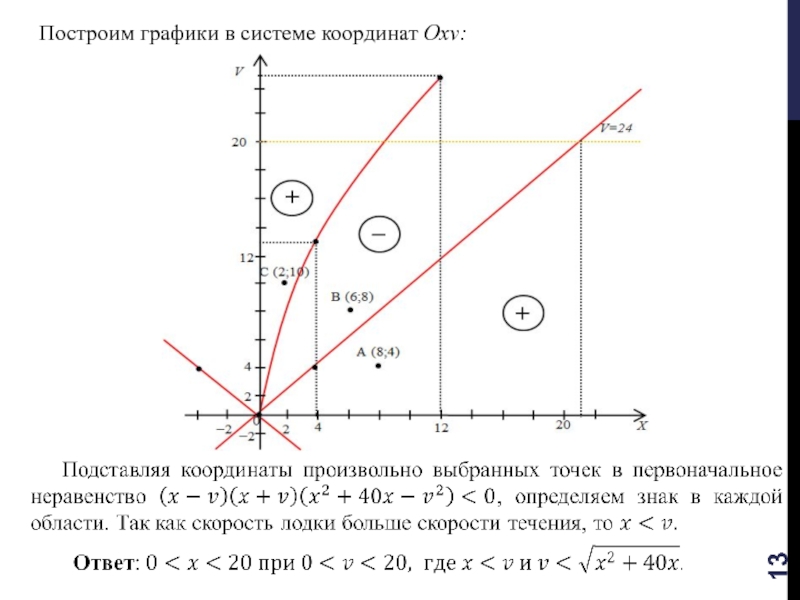 А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Выводы

1). Все, что лежит:

  • выше оси t – положительное;
  • ниже оси t – отрицательное;
  • на горизонтальной оси t – равно нулю.

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

  • График x(t) координаты – это прямая линия.
  • График v(t) скорости – горизонтальная прямая.
  • График a(t) ускорения лежит на оси t.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

  • График x(t) координаты – это правая ветвь параболы.
  • График v(t) скорости – наклонная прямая.
  • График a(t) ускорения – горизонтальная прямая.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

  • График x(t) координаты – это левая ветвь параболы.
  • График v(t) скорости – наклонная прямая.
  • График a(t) ускорения – горизонтальная прямая.

Графическое представление движения (равномерного и прямолинейного)

4.1

Средняя оценка: 4.1

Всего получено оценок: 147.

4.1

Средняя оценка: 4.1

Всего получено оценок: 147.

Большую часть информации о мире человек получает с помощью зрения. Поэтому одними из наиболее используемых способов описания физических явлений являются графики. Рассмотрим особенности графического представления движения.

График координаты

Движение тела состоит в изменении его координат с течением времени. У тела всегда есть некоторые координаты, на прямой – одна, на плоскости – две, в пространстве – три. А значит, для любой координаты можно построить график ее зависимости от времени. По оси абсцисс на графике откладываются единицы времени, по оси ординат – единицы расстояния. Точки на графике будут представлять координату тела в соответствующие моменты.

Равномерное движение

В простейшем случае тело равномерно движется вдоль прямой, для описания такого движения достаточно одной координаты. Формула перемещения при равномерном движении:

$$x=x_0+vt$$

Используя эту формулу, строим график.

Допустим, в начальный момент времени тело имеет координату 5, скорость движения 2. Получаем точки:

t

x

0

5

1

7

2

9

3

11

4

13

5

15

Построенный график – это прямая.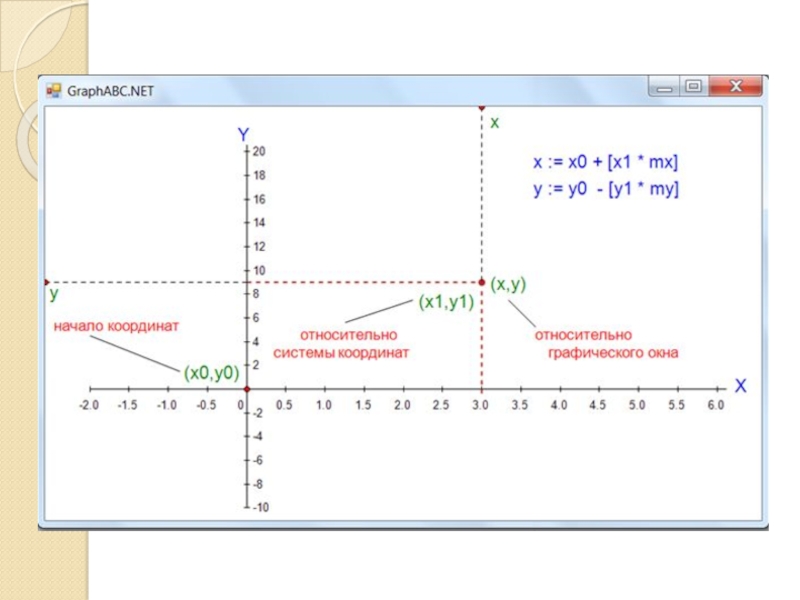 По нему можно найти координату тела в любой момент времени.

Графическое представление равномерного движения всегда представляет собой прямую, пересекающую ось ординат в точке, равную начальной координате. Наклон прямой характеризует скорость равномерного движения – чем она больше, тем круче поднимается график. Если скорость отрицательна – то график будет нисходящим.

Рис. 1. График координаты равномерного движения.

Неравномерное движение

Если тело движется неравномерно, и скорость его меняется, то график координаты будет более сложным.

Если тело сперва двигалось с одной скоростью, потом с другой, и так далее – он будет состоять из ряда прямолинейных участков, каждый из которых можно рассматривать, как отдельный график равномерного движения, при котором начальная координата участка равна конечной координате предыдущего участка. Например, пусть тело сперва двигается вперед (восходящая прямая), потом некоторое время стоит (горизонтальная прямая), а потом вернется (нисходящая прямая).

Получим график: Рис. 2. График координаты от времени в виде трапеции.

Наиболее сложный случай – когда тело постоянно плавно изменяет свою скорость. В этом случае график будет представлять собой плавную кривую. Например, если скорость равномерно увеличивается, то движение получается равноускоренным, и его графиком является восходящая парабола.

График скорости

Иногда удобно построить график скорости движения. Строится он точно так же, как и график координаты, но при этом по оси ординат откладываются значения скорости.

При равномерном движении скорость постоянна, а график постоянной величины представляет собой горизонтальную прямую. При нулевой скорости эта прямая совпадает с осью абсцисс.

Рис. 3. График скорости равномерного движения.

Если движение равноускоренное – то прямая будет восходящей или нисходящей.

График координаты и траектория

Иногда путают траекторию и график координаты. Это – не одно и то же.

Траектория – это линия, вдоль которой происходит движение. График же показывает зависимость координаты от времени. Например, если тело движется прямолинейно с остановками – его траектория будет прямой линией, а график координаты – ломанной, состоящей из наклонных и горизонтальных участков. Если тело движется равномерно по окружности, его траектория будет представлять собой круг, а графики обоих координат – синусоиды.

Что мы узнали?

Удобным способом описания движения является построение графиков координат. Для графического представления прямолинейного движения достаточно одного графика, для описания движения на плоскости – требуются два графика, в пространстве – три. Скорость также можно представить в виде графика.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

    Пока никого нет. Будьте первым!

Оценка доклада

4.1

Средняя оценка: 4.1

Всего получено оценок: 147.

А какая ваша оценка?

Что такое координатная плоскость? Определение, примеры, факты

Что такое координатная плоскость?

Координатная плоскость — это двумерная плоскость, образованная пересечением двух числовых линий. Одна из этих числовых линий представляет собой горизонтальную числовую линию, называемую осью x, а другая числовая линия представляет собой вертикальную числовую линию, называемую осью y. Эти две числовые линии пересекаются друг с другом перпендикулярно и образуют координатную плоскость, которая выглядит следующим образом:

Плоскость называется двумерной, потому что в любом месте этой плоскости, куда вы можете приложить палец, для определения местоположения этой точки потребуются две вещи — ее расстояние по оси x и его расстояние по оси y.

Левая и нижняя части плоскости имеют отрицательную ось x и отрицательную ось y для отрицательных целых чисел. Точка, в которой пересекаются числовые линии, называется началом координат.

Координатная плоскость — это инструмент, используемый для построения графиков точек, линий и других объектов. Он функционирует как карта, которая следует направлениям от одной точки к другой.

Похожие игры

Элементы координатной плоскости

Квадранты: Две числовые линии делят координатную плоскость на 4 области. Эти регионы называются Квадрантами. Квадранты обозначаются римскими цифрами, и каждый из этих квадрантов имеет свои собственные свойства.

Квадрант I: Верхний правый квадрант — это первый квадрант, обозначенный как Квадрант I. В этом квадранте оси x и оси y имеют положительные числа.

Квадрант II: Верхний левый Квадрант — это второй Квадрант, обозначенный как Квадрант II. В этом квадранте ось X имеет отрицательные числа, а ось Y имеет положительные числа.

Квадрант III: Нижний левый Квадрант — это третий Квадрант, обозначенный как Квадрант III. В этом квадранте и ось x, и ось y имеют отрицательные числа.

Квадрант IV: Нижний правый Квадрант — это четвертый Квадрант, обозначенный как Квадрант IV. В этом квадранте ось X имеет положительные числа, а ось Y имеет отрицательные числа.

Координата: Каждая точка на координатной плоскости выражается в виде упорядоченной пары (x,y), где x и y — числа, обозначающие положение точки относительно оси x и оси y.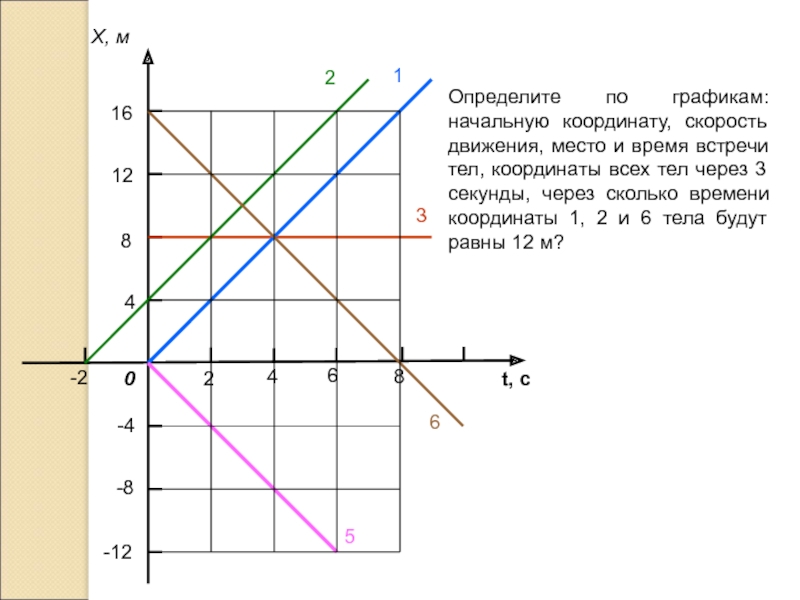 оси соответственно.

Например: Рассмотрим точку A на данном изображении:

Если мы хотим передать положение точки A, мы проверим, где она лежит относительно оси x и y соответственно.

 Здесь положение A по оси X равно 1 единице, а по оси Y равно 2 единицам, поэтому мы запишем положение A как A(1,2) на координатной плоскости.

Аналогичным образом мы можем найти положение любой точки на координатной плоскости, и она может принимать положительные или отрицательные значения в зависимости от квадранта, в котором она находится. Начало, очевидно; обозначается как (0,0)

Интересные факты

  1. Координатная плоскость была создана сотни лет назад. Эту систему обычно называют декартовой системой координат, потому что ее изобрел французский математик Рене Декарт.
  2. Точки на оси x имеют координату y 0, поэтому точки на оси x представлены как (x,0) и аналогичным образом точки на оси y имеют координату x 0, поэтому они представлены как ( 0,у).

Вывод
Координатная плоскость — это система построения графиков и описания точек и линий. Вертикальная (y) ось и горизонтальная (x) ось составляют координатную плоскость. В координатной плоскости четыре квадранта. Точка, где эти линии соединяются, называется началом координат (0, 0). Перейдите на SplashLearn, чтобы узнать больше о концепциях координатной плоскости.

Связанные рабочие листы

Решенные примеры 

В 1. В каких квадрантах координатной плоскости лежат следующие точки?

● A (–2, 4)

● B (2,5, 3,5)

● C (4, –2,2)

● D (6,5, 1)

Решение: 9000 5

Точка А находится в второй квадрант.

Точки B и D лежат в первом квадранте.

Точка C находится в четвертом квадранте.

В 2. Какие из следующих точек лежат на оси Y? Поясните свой ответ.

(i) (0, 3)          

(ii) (5, 0)          

(iii) (–2, 0)       

(iv) (0, –2)       

(v) (–1, 3)

Решение: (i) и (iv) лежат на оси y, так как координата x в этих точках равна нулю.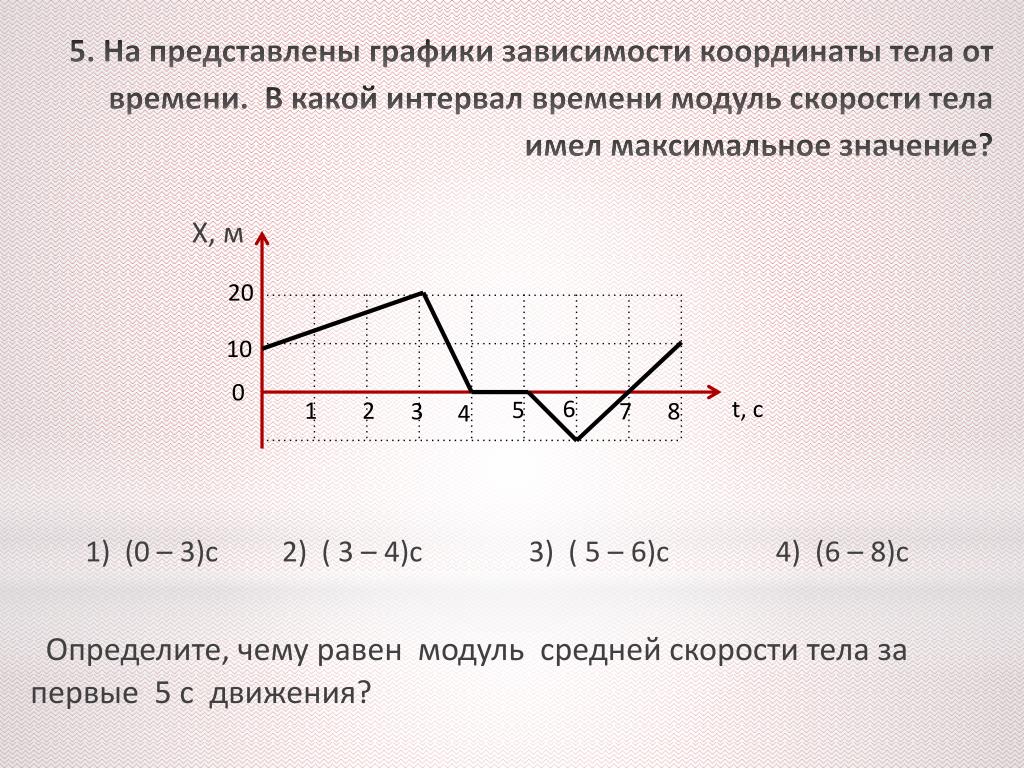

В 3. Вы находитесь в точке (−4, 3). Переместитесь на 5 единиц вправо и на 2 единицы вверх. Напишите координаты точки, куда вы добираетесь.

Решение:

Перемещение на 5 единиц вправо приведет к -4 + 5 = 1 по оси x.

Перемещение на 2 единицы вверх приведет к 3 + 2 = 5 по оси Y.

Итак, координаты точки, в которую мы попали, это (1, 5).

В 4. Каковы координаты точки, лежащей в начале координат?

Решение:

Поскольку точка находится в начале координат, координаты точки (0, 0).

Практические задачи

1

Какая из следующих точек находится в третьем квадранте?

(1, 5)

(–3, 6)

(2, 2)

(–8, –2)

Правильный ответ: (–8, –2)
Поскольку точки в в третьем квадранте обе координаты x и y имеют отрицательные числа.

2

Какая из следующих точек лежит в первом квадранте?

P (2, 5)

Q (–2, 4)

R (–1, –8)

S (4, –2)

Правильный ответ: P (2, 5)
P (2, 5). Здесь абсцисса и ордината точки положительны. Итак, он находится в первом квадранте.

3

Какая из следующих точек лежит на оси x?

(0, 1)

(1, 0)

(1, 1)

(4, −3)

Правильный ответ: (1, 0)
Для точки на оси x ордината должна быть равна нулю.

4

Начало в точке (0,0). Идите влево на четыре клетки. Затем поднимитесь на пять клеток вверх. В какой точке вы приземлитесь?

(4, 5)

(4, –5)

(–4, 5)

(–4, –5)

Правильный ответ: (–4, 5)
Из (0,0 ) когда мы идем на четыре клетки влево, мы приземляемся на координату (–4, 0) по оси X, теперь отсюда мы поднимаемся на пять клеток вверх, мы приземляемся на координату (–4, 5)

5

Какая связь между осью x и осью y на координатной плоскости?

Параллельно друг другу

Перпендикулярно друг другу

Пересекаются и (0,5)

Нет связи

Правильный ответ: Перпендикулярно друг другу
Две прямые пересекают друг друга перпендикулярно в начале координат и образуют координату плоскость

Часто задаваемые вопросы

Что такое начало координат на плоскости?

Начало координатной плоскости находится в точке нуля, где две ее оси перпендикулярно пересекают друг друга. Координаты начала координат (0, 0).

Что означает координата?

Координата — это упорядоченная пара значений x и y , которая помогает найти точку на плоскости, обозначенную как (x,y).

Когда удобна координатная плоскость?

При планировании расстановки различных предметов мебели в помещении создается двухмерная сетка, представляющая помещение. Для этого можно использовать приемлемую единицу измерения. Другой пример: воздушное движение управляется и регулируется с помощью координатной геометрии. Координаты рейса используются для описания текущего местоположения самолета.

Графики и координатная плоскость

Графики и координатная плоскость

Аннотация

Этот урок предназначен для ознакомления учащихся с построением упорядоченных графиков. пары чисел на координатной плоскости.

Цели

По окончании данного занятия учащиеся будут:

  • введены в декартову координатную плоскость
  • понимать четыре квадранта декартовой координатной плоскости
  • уметь наносить точки на плоскость
  • иметь возможность считывать координаты точки с графика
  • уметь указывать отношение подъема к пробегу для уклона

Стандарты

Упражнения и обсуждения на этом уроке касаются следующих Стандарты НКТМ:

Алгебра

Понимание закономерностей, взаимосвязей и функций

  • представлять, анализировать и обобщать различные шаблоны с помощью таблиц, графиков, слов и, по возможности, символические правила;
  • связывать и сравнивать различные формы представления отношений;
  • определить функции как линейные или нелинейные и сравнить их свойства с таблицами, графиками, или уравнения.

Представляйте и анализируйте математические ситуации и структуры, используя алгебраические символы.

  • развить начальное концептуальное понимание различных способов использования переменных;
  • исследовать отношения между символическими выражениями и графами линий, уделяя особое внимание внимание на значение перехвата и наклона;
  • использовать символическую алгебру для представления ситуаций и решения проблем, особенно тех, которые включать линейные отношения;
  • распознавать и генерировать эквивалентные формы для простых алгебраических выражений и решать линейные уравнения

Используйте математические модели для представления и понимания количественных отношений

  • Моделирование и решение контекстуализированных задач с использованием различных представлений, таких как графики, таблицы и уравнения

Требования к учащимся

  • Арифметика : Учащиеся должны уметь:
    • выполнять целочисленные и дробные арифметические операции
  • Алгебраический : Учащиеся должны уметь:
    • работа с очень простыми линейными алгебраическими выражениями
  • Технологические Студенты должны уметь:
    • выполнять основные манипуляции с мышью, такие как наведение, щелчок и перетаскивание
    • используйте браузер, такой как Netscape, для экспериментов с действиями

Подготовка учителей

Студентам понадобятся:

  • Доступ к браузеру
  • карандаш и миллиметровая бумага
  • Копии дополнительных материалов к мероприятиям:
    • Координаты Игровые предложения
    • Предложения по игре в лабиринт

Основные термины

Этот урок знакомит учащихся со следующими терминами посредством обсуждений:
  • координаты

План урока

Эти действия могут быть выполнены индивидуально или в группах до четырех студентов. Выделите 1-2 часа учебного времени на весь урок, если все части делаются в классе.

  1. Фокус и обзор

    Напомните учащимся, что они узнали на предыдущих уроках, что будет иметь отношение к этому уроку и/или пусть они начнут думать о словах и идеях этого урока.

    • Объективы

      Сообщите учащимся, что они будут делать и изучать сегодня. Скажи что-нибудь вроде это:

      • Сегодня, класс, мы будем учиться рисовать линии на координатной плоскости.
      • Мы собираемся использовать компьютеры для этого но, пожалуйста, не включайте свои компьютеры, пока я не попрошу вас. Я хочу показать вам немного о эта деятельность в первую очередь.
    • Ввод учителя
      • Вести обсуждение по номеру линия и координатная плоскость.
    • Методические рекомендации
      • Отработайте у учащихся навыки построения точечных графиков, попросив их сыграть Координаты! Игра Игра позволяет пользователям понять и попрактиковаться в использовании координатной плоскости для задания «адрес» или точное расположение конкретных точек.
    • Независимая практика
      • Предложите учащимся попрактиковаться в построении графиков на миллиметровка с использованием таблиц значений они сгенерированы на уроках по функциям и линейные функции.
      • Предложите учащимся проверить свои навыки, играя в Игра «Лабиринт».
    • Крышка
      • Вы можете снова собрать класс для обсуждения результатов. После того, как учащимся будет разрешено поделиться тем, что они нашли, подведите итоги. урок.

Альтернативные контуры

Этот урок можно перестроить несколькими способами.