Открытая Математика. Функции и Графики. Построение кривых, заданных параметрически
Построение кривых, заданных параметрически
При построении кривых, заданных параметрически: x = x (t), y = y (t), можно придерживаться следующего плана.
- Найти области определения Dx (t) и Dy (t) функций x (t) и y (t).
- Найти область определения Dt=Dxt∩Dyt функции, заданной параметрически.
- Решив уравнения x (t) = 0, y (t) = 0, найти точки пересечения с осями координат.
- Вычислить производные x′t и y′t.
- Определить производную y′x=y′tx′t. Найти критические точки.
- На каждом из интервалов, границами которых служат критические точки, определить знак производной
y′x
и промежутки возрастания и убывания функции y (x), заданной параметрически.
- Определить экстремумы функции, а также точки, касательная к которым вертикальна (производная y′x в этих точках обращается в бесконечность).
- Определить особые точки графика, в которых x′t=0 и (или) y′t=0.
- Найти пределы
limt→t0xt
и
limt→t0yt
в точках t0, лежащих на границах области определения.
- Если оба предела конечны, найти касательную к кривой в точке x0=limt→t0xt, y0=limt→t0yt.
- Если один из пределов конечен, а второй бесконечен, то кривая имеет горизонтальную y = y0 или вертикальную x = x0 асимптоту.
- Если оба предела бесконечны, то найти наклонную касательную, вычислив пределы k=limt→t0ytxt, b=limt→t0yt-kxt. Если один из этих пределов не существует, то асимптоты нет.
- Вычислить производную
y′′xx=y′′ttx′t-y′tx′′ttx′t3
и определить точки перегиба функции и направление выпуклости на каждом из интервалов, ограниченных точками перегиба или точками, в которых вторая производная не существует.
- Выяснить, существуют ли точки самопересечения графика функции, решив систему {xt1=xt2yt1=yt2, t1≠t2
- Проверить график функции на симметричность.
- График функции симметричен относительно точки (a; b), если при любом t можно найти такое t1, что {xt+xt1=2ayt+yt1=2b.
- График функции симметричен относительно прямой ax + by + c = 0, если при любом t можно найти такое t1, что
{axt1+xt+byt1+yt+2c=0bxt1-xt=ayt1-yt.
В частности, график функции симметричен относительно прямой
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».
примеров исчисления | Параметрические уравнения и полярные координаты
Шаг 1
Настройте параметрическое уравнение для решения уравнения для .
Шаг 2
Перепишите уравнение как .
Шаг 3
Вычтите из обеих частей уравнения.
Шаг 4
Разделите каждое слагаемое на и упростите.
Нажмите, чтобы увидеть больше шагов…Шаг 4.1
Разделите каждое слагаемое на .
Шаг 4.2
Упростите левую сторону.
Нажмите, чтобы увидеть больше шагов…Шаг 4.2.1
Отменить общий множитель .
Нажмите, чтобы увидеть больше шагов…Шаг 4.2.1.1
Отменить общий множитель.
Шаг 4.2.1.2
Разделить на .
Шаг 4.3
Упростите правую сторону.
Нажмите, чтобы увидеть больше шагов…Шаг 4.3.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…Шаг 4.3.1.1
Отмените общий множитель и .
Шаг 4.3.1.1.1
Вычесть из .
Шаг 4.3.1.1.2
Отменить общие коэффициенты.
Нажмите, чтобы увидеть больше шагов…Шаг 4.3.1.1.2.1
Умножить на .
Шаг 4.3.1.1.2.2
Отменить общий множитель.
Шаг 4.3.1.1.2.3
Перепишите выражение.
Шаг 4.3.1.2
Поместите минус перед дробью.
Этап 5
Замените в уравнении на , чтобы получить уравнение в терминах .
Шаг 6
Упрощение .
Нажмите, чтобы увидеть больше шагов…Шаг 6.1
Переписать как .
Шаг 6.2
Расширение с использованием метода FOIL.
Нажмите, чтобы увидеть больше шагов…Шаг 6.2.1
Примените свойство распределения.
Шаг 6.2.2
Примените свойство распределения.
Шаг 6.2.3
Примените свойство распределения.
Шаг 6.3
Упростите и объедините подобные термины.
Нажмите, чтобы увидеть больше шагов.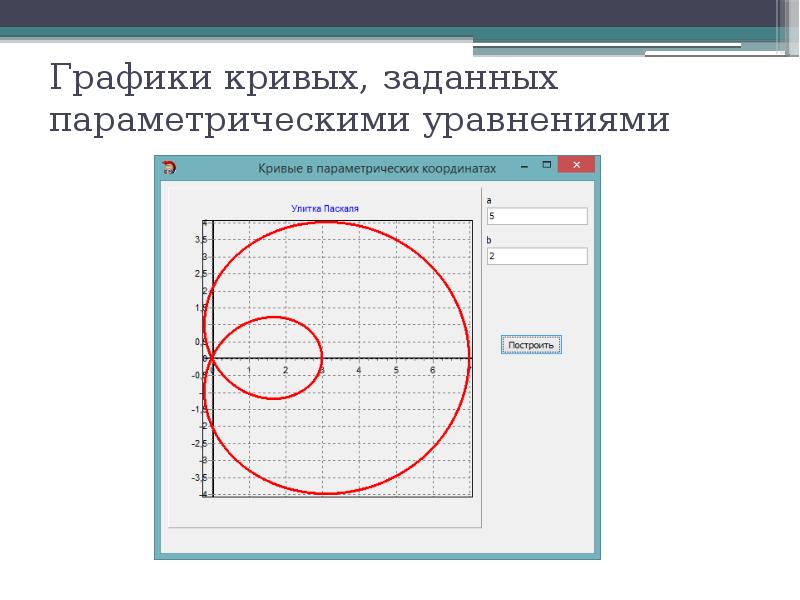
..Шаг 6.3.1
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…Шаг 6.3.1.1
Умножение .
Нажмите, чтобы увидеть больше шагов…Шаг 6.3.1.1.1
Умножить на .
Шаг 6.3.1.1.2
Возведение в степень .
Шаг 6.3.1.1.3
Возведение в степень .
Шаг 6.3.1.1.4
Используйте правило степени для объединения показателей степени.
Шаг 6.3.1.1.5
Добавить и .
Шаг 6.3.1.1.6
Умножить на .
Шаг 6.3.1.2
Умножить .
Нажмите, чтобы увидеть больше шагов…Шаг 6.3.1.2.1
Умножить на .
Шаг 6.3.1.2.2
Умножить на .
Шаг 6.3.1.3
Умножить .
Нажмите, чтобы увидеть больше шагов…Шаг 6.3.1.3.1
Умножить на .
Шаг 6.3.1.3.2
Умножить на .
Шаг 6.3.1.4
Умножение .
Нажмите, чтобы увидеть больше шагов…Шаг 6.3.1.4.1
Умножить на .
Шаг 6.3.1.4.2
Умножить на .
Шаг 6.3.1.4.3
Умножить на .
Шаг 6.3.1.4.4
Умножить на .
Шаг 6.3.2
Вычесть из .
Шаг 6.4
Упростите каждый термин.
Нажмите, чтобы увидеть больше шагов…Шаг 6.4.1
Отменить общий множитель .
Нажмите, чтобы увидеть больше шагов…Шаг 6.4.1.1
Умножить на .
Шаг 6.4.1.2
Фактор из .
Шаг 6.4.1.3
Отменить общий множитель.
Шаг 6.4.1.4
Перепишите выражение.
Шаг 6.4.2
Переписать как .
Введите СВОЮ задачуИсчисление II. Параметрические уравнения и кривые (практические задачи)
Онлайн-заметки Пола
Главная
/
Исчисление II
/
Параметрические уравнения и полярные координаты
/ Параметрические уравнения и кривые
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 9.1: Параметрические уравнения и кривые 92}\hspace{0.5in}0 \le t \le 3\) Решение
Ваш комментарий будет первым