График функции с двумя переменными онлайн: Построение графика функции онлайн

Линейная функция и ее график (В.А.Тарасов) 7 класс онлайн-подготовка на Ростелеком Лицей

Напоминание некоторых теоретических фактов и решение опорной задачи

 

В предыдущих уроках мы изучали линейное уравнение с двумя переменными, это уравнение вида , . Мы выяснили, что графиком данного уравнения является прямая. Рассмотрим пример:

 

Пример 1:

 (1)

Перепишем его таким образом, чтобы у был в одной части, а все остальное в другой:

Сократим на 2:

Перенесем у в левую часть, а все остальное в правую:

 (2)

Мы получили частный случай уравнения 1, в котором  стоит обособленно в левой части, графиком обоих выражений будет одна и та же прямая, но запись 2 мы будем называть линейной функцией у от х.

Построим график данной функции, для этого составим таблицу:

х	0	1,5
у	-3	0

Рис. 1. График функции y=2x-3

 

Выведение линейной функции и ее параметров в общем случае, введение новых терминов

 

 

Определим линейную функцию в общем случае из линейного уравнения с двумя переменными:

 

Поскольку  можем обе части поделить на b:

Введем более удобные обозначения:

,

Получаем выражение:

 (3)

Для примера №1 ,

Таким образом, пара чисел k и m задают конкретную линейную функцию.

Введем некоторую терминологию. В линейной функции переменную х называют независимой переменной или аргументом функции, мы сами можем выбирать произвольное значение х и по нему находить соответствующее значение у.

 называют зависимой переменной или функцией.

Линейная функция характеризуется тем, что если задано значение х, можно сразу получить значение у. у – это линейная функция от х.

Найдем для линейной функции в общем виде (3) точки пересечения с осями. Для всех точек на оси у характерно то, что их абсцисса – координата х, равна нулю.

, ;

Точка пересечения с осью у: (0, m)

Отсюда геометрический смысл переменной m – это ордината точки пересечения прямой 3 с осью у. Параметр m однозначно задает точку пересечения прямой 3 с осью ординат.

Параметр  носит название угловой коэффициент.

Для всех точек на оси х характерно то, что их ордината равна нулю. Найдем точку пересечения нашей функции с осью х:

, , ,

Точка пересечения с осью х: ()

 

Решение примера, выявление свойств параметров линейной функции

 

 

Пример 2:

 

Построим графики двух линейных функций:  (4),  (5)

В функции 4

В функции 5

Для построения графиков составим таблицы, в которых запишем точки их пересечения с осями координат:

х	0	-3
у	m=3	0

Таблица для функции 4;

х	0	3
у	m=3	0

Таблица для функции 5;

Рис.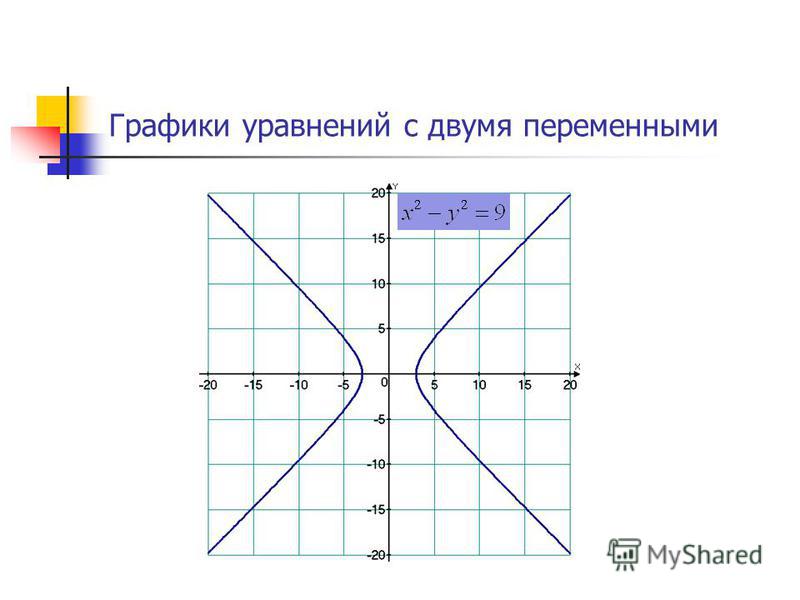 2. Графики функций y=-x+3 и y=x+3

Итак, из построения мы видим, что когда  (прямая ) угол  между прямой и положительным направлением оси х острый, а когда  (прямая ) угол  между прямой и положительным направлением оси х тупой.

Корнем функции 4 является число -3, потому что именно при этом значении х функция обращается в ноль.

Корнем функции 5 является число 3, так как при данном значении х функция обращается в ноль.

Отметим, что решением следующей системы:

Является точка (0; 3).

 

Решение типовых задач

 

 

Пример 3 – найти k и m:

 

Задано линейное уравнение, так как х и у стоят в первой степени, с двумя переменными.

Чтобы найти k и m, выполним преобразования:

Запишем полученное выражение в стандартном виде:

Отсюда очевидно, что , а

Пример 4 – найти k и m:

Преобразуем правую часть:

Запишем полученное выражение в стандартном виде:

Отсюда очевидно, что , а

Итак, одна из стандартных задач – это нахождение по заданному линейному уравнению параметров линейной функции k и m.

Еще две стандартные задачи – по заданному значению х найти у и наоборот, по заданному значению у найти х. Рассмотрим пример.

Пример 5 – найти значение у при :

Такую задачу иногда называют прямой задачей.

Пример 6 – найти значение аргумента, если :

Эта задача называется обратной.

 

Выводы по уроку

 

 

Вывод: в данном уроке мы рассмотрели линейную функцию как в частных случаях, так и в общем виде, определили параметры линейной функции и их значение, ввели некоторые новые термины, научились решать элементарные типовые задачи.

 

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал FizMat.by (Источник).

 

Рекомендованное домашнее задание

Задание 1: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 317, ст.74;

Задание 2: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 319, ст.74;

Задание 3: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра 7, № 322, ст.75;

 

График линейного уравнения с двумя переменными – онлайн-тест от Skills4u

Зарегистрируйся и получи 7 дней бесплатного доступа к тренажерам и персональный план прокачки знаний до 100%!

Вопросов в тесте: 15

Среднее время прохождения: ~10:00

Зарегистрируйся и получи персональный план прокачки знаний до 100%!

Как работает платформа Skills4u

Тестирование по предмету за класс

Платформа определит, какие темы сформированы слабо и составит индивидуальный план обучения

Персональный план обучения

План обучения и повторений поможет ученику в закреплении всех необходимых тем по предмету

Закрепление темы на 100%

Платформа напомнит и проконтролирует все повторения для закрепления каждой темы на 100%

Проработка слабых тем с предыдущих классов

Чтобы идеально овладеть предметом, рекомендуем закрепить пробелы, начиная с самых простых тем

Почему нужно пройти общее тестирование по алгебре за 7 класс, а не по отдельной теме «График линейного уравнения с двумя переменными: ax+by+c=0»

Пройдя тестирование за класс вы получите ПОЛНУЮ КАРТИНУ ЗНАНИЙ ПО ВСЕМ ТЕМАМ.
Такой подход позволит глубинно проанализировать знания, вывести успеваемость и понимание предмета на качественно новый уровень.

Пройдя тестирование по одной теме вы получите РЕЗУЛЬТАТ ЗНАНИЙ ТОЛЬКО ЭТОЙ ТЕМЫ, которая, возможно, плохо изучена. Такой метод не является комплексным и дает лишь точечное понимание знаний по предмету.

Зарегистрироваться и пройти тестирование

Хотите научиться без ошибок строить график линейного уравнения с 2 переменными? Мы подготовили тест для учеников 7 классов средней школы. Этот проверочный тест покажет, насколько хорошо вы усвоили тему, изучаемую на уроках алгебры.

Каждый желающий может пройти тест «График линейного уравнения с двумя переменными: ax+by+c=0» за 7 класс совершенно бесплатно. Это займет не более 5-7 минут. Всего в тесте 15 вопросов, на которые нужно дать ответ. Чертить графики не придется: только выбрать верный вариант из 4-х, представленных на экране. Это очень экономит время и избавляет от необходимости искать ручку и тетрадку.

Итак, приступаем. Вам нужно внимательно прочитать задание и выбрать график линейного уравнения онлайн. Он должен соответствовать заданной функции. Наведите курсор на правильный ответ и нажмите кнопку. Если вы ошиблись, загорится красный свет, но в то же время на экране появится и верный вариант, подсвеченный зеленым. Выполнение задания продолжится только после того, как вы поймете, где ошиблись, и нажмете кнопочку «Продолжить». Листать учебник или справочник не потребуется, система сама подскажет вам, как решать график линейного уравнения.

После завершения тестирования образовательная платформа Skills4u анализирует ваши ответы, учитывает время, потраченное на выполнение заданий. Если результат высокий, ваши заслуги будут отмечены. Если же построение графиков линейного уравнения дается вам с трудом, количество ошибок велико в процентном отношении, рекомендуем зарегистрироваться на сайте и начать заниматься на наших интерактивных тренажерах.

Для того, чтобы полезный учебный навык – решение линейных уравнений с графиком – остался в памяти навсегда, нужно отработать его на нашем интеллектуальном онлайн-тренажере. Очень важно вернуться к выполнению заданий в тот же день через несколько часов, а затем заниматься последующие 4-5 дней без перерыва, чтобы навык закрепился в памяти. Для этого потребуется оплаченный доступ к ресурсам образовательной платформы Skills4u.

Если вас интересует только график линейного уравнения за 7 класс, можно оплатить конкретный навык – цена чисто символическая. Но мы рекомендуем оформить расширенный доступ к тренажерам по различным предметам на месяц, полугодие или полный учебный год.

Как растут результаты учеников
после занятий на тренажерах Skills4u

Занятия
на Skills4u

Занятия
с учебником

Успеваемость

Мотивация

Внимательность

Скорость

Самостоятельность

Запоминание

Первичный Тест «График линейного уравнения с двумя переменными: ax+by+c=0» по алгебре за 7 класс онлайн и бесплатно предоставляется всем желающим.

Советуем пройти тестирование за весь 7 класс по алгебре, чтобы узнать пробелы в знаниях по всем темам и получить индивидуальный план обучения.

После регистрации вы получите 7 дней бесплатного доступа, чтобы увидеть первые результаты занятий и оценить эффективность тренажеров.

Зарегистрироваться и пройти тестирование

Регулярно занимаясь в удобное время, вы научитесь строить график линейного уравнения с двумя уравнениями, решать задачи по алгебре и геометрии, повысите свой рейтинг и начнете получать только высокие оценки на уроках. Проверено! Именно так работает наша уникальная методика, которая находит индивидуальный подход к каждому ученику!

А для комплексного результата пройдите общее тестирование за
класс! Узнайте пробелы в знаниях по всем темам

Ученик

Занимайся 20 минут в день и прокачай знания по школьной программе за месяц!

Родитель

Наслаждайтесь прогрессом вашего ребенка в школе и на платформе

Учитель/
репетитор

Задавайте и проверяйте домашние задания прямо на платформе

Зарегистрироваться и пройти тестирование

71000

---

учеников уже занимаются с нами

13.

1: Функции нескольких переменных

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

9039

• OpenStax
• OpenStax

Наш первый шаг — объяснить, что такое функция более чем одной переменной, начав с функций двух независимых переменных. Этот шаг включает в себя определение домена и диапазона таких функций, а также обучение их графическому отображению. Мы также исследуем способы соотнесения графиков функций в трех измерениях с графиками более знакомых плоских функций.

Функции двух переменных

Определение функции двух переменных очень похоже на определение функции одной переменной. Основное отличие состоит в том, что вместо отображения значений одной переменной в значения другой переменной мы отображаем упорядоченные пары переменных в другую переменную.

2\) к уникальному вещественному числу \(z\). Множество \(D\) называется областью определения функции. Диапазон \(f\) — это множество всех действительных чисел \(z\), у которых есть хотя бы одна упорядоченная пара \((x,y)∈D\), такая, что \(f(x,y)=z \), как показано на рисунке \(\PageIndex{1}\). 92\). Записанное в нотации построителя наборов, это можно было бы записать как \(\{ (x, y) | x \in \rm I\!R, y \in \rm I\!R \}\).

Чтобы определить диапазон, сначала выберите значение для z . Нам нужно найти решение уравнения \(f(x,y)=z,\) или \(3x−5y+2=z.\). Одно такое решение можно получить, сначала установив \(y=0\ ), что дает уравнение \(3x+2=z\). Решением этого уравнения является \(x=\dfrac{z−2}{3}\), что дает упорядоченную пару \(\left(\dfrac{z−2}{3},0\right)\) как решение уравнения \(f(x,y)=z\) для любого значения \(z\). Таким образом, областью действия функции являются все действительные числа, или \((-\infty, \infty)\). 92≤4\), границей которого является окружность радиуса \(2\).

Диапазон: \([0,6].\)

График функций двух переменных

Предположим, мы хотим построить график функции \(z=f(x,y).\). Эта функция имеет две независимые переменные (\(x\) и \(y\)) и одну зависимая переменная \((z)\). При построении графика функции \(y=f(x)\) одной переменной мы используем декартову плоскость. Мы можем изобразить любую упорядоченную пару \((x,y)\) на плоскости, и с каждой точкой на плоскости связана упорядоченная пара \((x,y)\). В функции двух переменных каждая упорядоченная пара \((x,y)\) в области определения функции отображается в действительное число \(z\). Следовательно, график функции \(f\) состоит из упорядоченных троек \((x,y,z)\). График функции \(z=f(x,y)\) двух переменных называется поверхностью.

Чтобы лучше понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте, что система координат \((x,y)\) лежит плоско. Тогда каждая точка области определения функции f имеет связанное с ней уникальное \(z\)-значение. Если \(z\) положительна, то точка графика находится выше плоскости \(xy\), если \(z\) отрицательна, то точка графика находится ниже плоскости \(xy\). Множество всех нанесенных на график точек становится двумерной поверхностью, являющейся графиком функции \(f\). 92 &≤ 16. \end{align*}\]

Это круг радиуса \(4\) с центром в \((3,2)\). Еще одно ограничение состоит в том, что и \(x\), и \(y\) должны быть неотрицательными. Когда \(x=3\) и \(y=2, \quad f(x,y)=16.\) Обратите внимание, что любое значение может быть нецелым числом; например, в месяц можно продать \(2,5\) тыс. орехов. Таким образом, домен содержит тысячи точек, поэтому мы можем рассматривать все точки в пределах диска. Для любого \(z<16\) мы можем решить уравнение \(f(x,y)=16:\) 92 &=16−z. \end{align*}\]

Поскольку \(z<16,\) мы знаем, что \(16−z>0,\), то предыдущее уравнение описывает окружность с радиусом \(\sqrt{16−z} \) с центром в точке \((3,2)\). Поэтому. диапазон \(f(x,y)\) равен \(\{z∈\mathbb{R}|z≤16\}.\) График \(f(x,y)\) также является параболоид, и этот параболоид направлен вниз, как показано на рисунке.

Рисунок \(\PageIndex{5}\): График заданной функции двух переменных также является параболоидом.

Кривые уровня

Если туристы идут по извилистым тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются тропы. А 9Топографическая карта 0040 содержит изогнутые линии, называемые изолиниями. Каждая контурная линия соответствует точкам на карте с одинаковой высотой (рис. \(\PageIndex{6}\)). Линия уровня функции двух переменных \(f(x,y)\) полностью аналогична изолинии на топографической карте.

Рисунок \(\PageIndex{6}\): (a) Топографическая карта Башни Дьявола, Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутую местность. (b) Перспективное фото Башни Дьявола показывает, насколько круты ее стороны. Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты. 92=5.\]

Это уравнение описывает окружность с центром в начале координат и радиусом \(\sqrt{5}\). Использование значений \(c\) между \(0\) и \(3\) дает другие круги, также центрированные в начале координат. Если \(c=3\), то окружность имеет радиус \(0\), поэтому она состоит только из начала координат. Рисунок \(\PageIndex{7}\) представляет собой график кривых уровня этой функции, соответствующих \(c=0,1,2,\) и \(3\). Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя в квадрат обе стороны. Здесь это не так, потому что диапазон функции квадратного корня неотрицательный. 92}  \end{align*}\]

Теперь, когда у нас есть \(f\) в этой форме, мы можем увидеть, насколько большим может быть подкоренное число. Поскольку мы вычитаем из \(16,\) два полных квадрата, мы знаем, что значение подкоренного числа не может быть больше, чем \(16.\)  В точке \((1, -2),\) мы можем видеть подкоренное число будет равно 16 (поскольку в этот момент мы будем вычитать \(0\) из \(16\).  Это дает нам максимальное значение \(f\), то есть \(f(1, -2) = \sqrt{16} = 4.\)

Таким образом, диапазон этой функции равен \([0, 4].\) 92\). Вертикальная трасса функции может быть либо набором точек, решающим уравнение \(f(a,y)=z\) для данной константы \(x=a\), либо \(f(x,b )=z\) для заданной константы \(y=b. \)

Пример \(\PageIndex{5}\): поиск вертикальных следов

Поиск вертикальных следов для функции \(f(x,y)= \sin x \cos y\), соответствующие \(x=−\dfrac{π}{4},0,\) и \(\dfrac{π}{4}\), и \(y=−\dfrac {π}{4},0\) и \(\dfrac{π}{4}\).

Решение

Первое множество \(x=−\dfrac{π}{4}\) в уравнении \(z=\sin x \cos y:\)

\(z=\sin(-\dfrac{π}{4})\cos y=-\dfrac{\sqrt{2}\cos y}{2}≈-0,7071\cos y.\)

Это описывает косинусный график на плоскости \(x=−\dfrac{π}{4}\). Другие значения \(z\) приведены в следующей таблице.

Вертикальные трассы, параллельные \(xz-плоскости\) для функции \(f(x,y)=\sin x \cos y\)

\(с\)	Вертикальная трассировка для \(x=c\)
\(−\dfrac{π}{4}\)	\(z=-\dfrac{\sqrt{2}\cos y}{2}\)
0	\(г=0\)
\(\dfrac{π}{4}\)	\(z=\dfrac{\sqrt{2}\cos y}{2}\)

Аналогичным образом мы можем подставить \(y\)-значения в уравнение \(f(x,y)\), чтобы получить трассы в \(yz\)-плоскости, как указано в следующую таблицу.

Вертикальные трассы, параллельные плоскости \(yz\) для функции \(f(x,y)=\sin x \cos y\)

\(г\)	Вертикальная трассировка для \(y=d\)
\(\dfrac{π}{4}\)	\(z=\dfrac{\sqrt{2}\sin x}{2}\)
0	\(г=\грех х\)
\(−\dfrac{π}{4}\)	\(z=\dfrac{\sqrt{2}\sin x}{2}\)

Три трассы в \(xz\)-плоскости являются функциями косинуса; три следа в \(yz\)-плоскости являются синусоидальными функциями. Эти кривые появляются на пересечениях поверхности с плоскостями \(x=−\dfrac{π}{4},\quad x=0,\quad x=\dfrac{π}{4}\) и \(y =−\dfrac{π}{4},\quad y=0,\quad y=\dfrac{π}{4}\), как показано на следующем рисунке. 92\). Эта функция описывает параболу, раскрывающуюся вниз в плоскости \(y=3\).

Функции двух переменных могут создавать эффектные поверхности. На рисунке \(\PageIndex{11}\) показаны два примера.

Рисунок \(\PageIndex{11}\): Примеры поверхностей, представляющих функции двух переменных: (а) комбинация степенной функции и синусоидальной функции и (б) комбинация тригонометрической, экспоненциальной и логарифмической функций.

Функции более чем двух переменных 92)\sin t−(3x+5y)\cos t.\]

В первой функции \((x,y,z)\) представляет точку в пространстве, а функция \(f\) отображает каждую точку пространства к четвертой величине, такой как температура или скорость ветра. Во второй функции \((x,y)\) может представлять точку на плоскости, а \(t\) может представлять время. Функция может сопоставить точку на плоскости третьей величине (например, давлению) в данный момент времени \(t\). Метод нахождения области определения функции более чем двух переменных аналогичен методу для функций одной или двух переменных. 92−4\} \номер\]

Функции двух переменных имеют кривые уровня, которые отображаются как кривые в \(xy-плоскости.\) Однако, когда функция имеет три переменные, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных .

Определение: поверхность уровня функции трех переменных

Для данной функции \(f(x,y,z)\) и числа \(c\) в диапазоне \(f\) Поверхность функции трех переменных определяется как множество точек, удовлетворяющих уравнению \(f(x,y,z)=c.\) 93\) и могут быть изучены с помощью кривых уровня и вертикальных следов.

Набор кривых уровня называется контурной картой.

Ключевые уравнения

• Вертикальная трассировка

\(f(a,y)=z\) для \(x=a\) или \(f(x,b)=z\) для \(y=b\)

• Ровная поверхность функция трех переменных

\(f(x,y,z)=c\)

Глоссарий

контурная карта

график различных кривых уровня заданной функции \(f(x,y)\) 92\) на уникальное вещественное число \(z\)

график функции двух переменных

набор упорядоченных троек \((x,y,z)\), который удовлетворяет уравнению \(z=f(x,y)\) в трехмерном декартовом пространстве

кривая уровня функции двух переменных

множество точек, удовлетворяющих уравнению \(f(x,y)=c\) для некоторого действительного числа \(c\) в диапазоне \(f\)

поверхность уровня функции трех переменных

множество точек, удовлетворяющих уравнению \(f(x,y,z)=c\) для некоторого действительного числа \(c\) в диапазоне \(f\)

поверхность

график функции двух переменных \(z=f(x,y)\)

вертикальная трасса

множество упорядоченных троек \((c,y,z)\), которое решает уравнение \(f(c,y)=z\) для данной константы \(x=c\) или множество упорядоченных троек \((x,d,z)\), которая решает уравнение \(f(x,d)=z\) для заданной константы \(y=d\)

Авторы

---

Эта страница под заголовком 13. 1: Функции нескольких переменных распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована OpenStax.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   хайтоп

   решения

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   да

2. Теги

   1. расчет: да
   2. контурная карта
   3. функция двух переменных
   4. график функции двух переменных
   5. кривая уровня функции двух переменных
   6. поверхность уровня функции трех переменных
   7. поверхность
   8. вертикальная трасса

Калькулятор функции упорядоченной пары — Googlesuche

AlleBilderShoppingVideosMapsNewsBücher

suchoptionen

Упорядоченные пары — Tiger Algebra Solver

Бесплатный алгебраический решатель и алгебраический калькулятор, показывающий пошаговые решения. Нет загрузки или регистрации. Доступен как веб-сайт для мобильных и настольных компьютеров, а также …

Калькулятор упорядоченных пар — Math Celebrity

www.mathcelebrity.com › упорядоченная пара

Калькулятор свободных упорядоченных пар. Этот калькулятор выполняет следующие преобразования: * Оценка упорядоченных пар и симметричные точки, включая абциссу и … (4,9),(2,10)} представляют собой фу

www.mathcelebrity.com › search

Как работает Калькулятор функциональных тестов? Бесплатный калькулятор функциональных тестов — проверяет, представляет ли набор упорядоченных пар функцию

Ähnliche Fragen

Как найти функцию упорядоченных пар?

Что такое калькулятор заказанных пар?

Калькулятор функции упорядоченной пары (KZG2MI)

xizmbe.schnelltest-staufen.de

Калькулятор функции упорядоченной пары Набор первых компонентов каждого заказанного … 7 Поддержка клиентов Определение функций с помощью упорядоченных пар, таблиц и.

Калькулятор упорядоченных пар — Cuemath

www.cuemath.com › калькуляторы › расчет упорядоченных пар…

«Калькулятор упорядоченных пар» — это бесплатный онлайн-инструмент, который вычисляет упорядоченные пары для заданного уравнения. В этом калькуляторе вы можете ввести уравнение …

Предалгебраические примеры | Поиск решений упорядоченных пар — Mathway

www.mathway.com › примеры › предварительная алгебра › найти…

Выберите любое значение x x, которое находится в домене, чтобы подставить его в уравнение. Шаг 2. Выберите 0 0 вместо x x, чтобы найти упорядоченную пару.

Примеры алгебры | Функции | Поиск упорядоченных парных решений

www.mathway.com › примеры › поиск упорядоченных пар…

Бесплатное средство решения математических задач отвечает на ваши домашние вопросы по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми объяснениями , …

Упорядоченные пары, графические линейные. .. Пошаговое решение математических задач

quickmath.com › Статьи по математике › Линейные уравнения

В этой статье мы узнаем об упорядоченных парах, графических линейных уравнениях, наклоне-перехвате и точечно-наклонные формы.

Калькулятор заказанной пары: все, что вам нужно знать | It Lesson Education

itlessoneducation.com › калькулятор упорядоченных пар

25.05.2022 · Калькулятор упорядоченных пар – это бесплатный онлайн-калькулятор. Он отображает упорядоченную пару для данного уравнения. Любой онлайн-калькулятор заказанных пар …

Первый элемент упорядоченной пары: Второй элемент упорядоченной пары
Это координата x: Значит, это координата y
Представляет расстояние точки от оси y: Представляет расстояние точки от ось x
Представляет горизонтальное расстояние точки от начала координат: Представляет вертикальное расстояние точки от начала координат

Калькулятор поиска упорядоченной пары — факторинговые полиномы

factoring-polynomials.