Построение графиков функций. КОМПАС-3D V10 на 100 %
Построение графиков функций
В завершение практического раздела данной главы я решил добавить еще один параграф, описывающий способы построения графиков всевозможных функций в системе КОМПАС-График. Этот вопрос неоднократно поднимался пользователями во время работы с программой, причем многие из них даже не подозревали о заложенной в КОМПАС-График возможности построения функций по их уравнениям.
Специально для этой цели в системе есть отдельное приложение – библиотека FTDraw, которую вы можете найти в разделе Прочие менеджера библиотек. Библиотека позволяет выполнять следующие действия (рис. 2.144):
• строить графики функциональных зависимостей в декартовых координатах;
• строить графики функций в полярных координатах;
• строить графики по загруженным табличным данным (взятым, например, из табличного редактора Excel).
Рис. 2.144. Библиотека FTDraw
После запуска библиотеки в менеджере откроется ее меню, состоящее из двух команд: Библиотека построения графиков FTDraw и Простейший математический калькулятор.
Внимание!
Перед тем как запускать библиотеку, обязательно создайте (или сделайте активным) чертеж или фрагмент.
Давайте рассмотрим пример построения графика какой-либо сложной функции в декартовых координатах. Предположим, что рассматривается функция вида y(x) = 4?x + 3cos(x) + 2ln(x) в диапазоне от 0,1 до 100. Щелкните на первой из больших квадратных кнопок главного окна библиотеки, чтобы перейти в режим построения графиков в декартовых координатах. В результате перед вами откроется новое окно (рис. 2.145), в котором необходимо задать уравнение, по которому будет строиться график, а также параметры построения.
Рис. 2.145. Построение графиков функций в декартовых координатах
По умолчанию в поле для введения функции стоит Sqrt(x), что означает, что система настроена на построение графика y(x) = ?x. Данная утилита имеет весьма несложный синтаксис, к тому же вы всегда можете воспользоваться подсказкой при выборе нужной функции, щелкнув правой кнопкой мыши в поле, где нужно вводить формулу (рис. 2.146).
Данная утилита имеет весьма несложный синтаксис, к тому же вы всегда можете воспользоваться подсказкой при выборе нужной функции, щелкнув правой кнопкой мыши в поле, где нужно вводить формулу (рис. 2.146).
Рис. 2.146. Подсказка для выбора и вставки функций
Пользуясь приведенными подсказками и клавиатурой, введите в поле для функций следующую строку: 4*Sqrt(x)+3*Cos(x)+2*Ln(x). После этого в полях Пределы изменения Х задайте нужный диапазон, а в поле Количество точек установите значение 50. Нажмите кнопку Указать положение базовой точки графика
после чего щелкните в точке, где планируете поместить начало координат создаваемого графика. После задания точки система вернется к окну задания функциональных зависимостей, в котором теперь должна активироваться кнопка Построить график
Щелкните на этой кнопке, затем нажмите OK, чтобы завершить построение. Если вы все сделали правильно, в результате должен получиться график, показанный на рис. 2.147.
Рис. 2.147. График функции в декартовых координатах
2.147. График функции в декартовых координатах
В качестве еще одного примера приведу порядок построения графика в полярных координатах. Для рассмотрения возьмем несложную и достаточно известную спираль Архимеда, уравнение которой в полярных координатах имеет вид r = kj, где k – произвольный коэффициент, отличный от 0.
Запустите вновь библиотеку FTDraw и нажмите вторую справа большую кнопку, запустив режим построения графиков в полярных координатах. В строке для формул введите значение 2*Х, диапазон задайте от 0 до 20*Pi, а количество точек установите равным 200 (рис. 2.148).
Рис. 2.148. Построение графика функции в полярных координатах
После того как вы укажете начальную точку для построения, нажмите по очереди кнопки Построить график и ОK. В результате вы получите архимедову спираль, построенную на фрагменте в системе КОМПАС-3D (рис. 2.149).
Рис. 2.149. Архимедова спираль
Данный текст является ознакомительным фрагментом.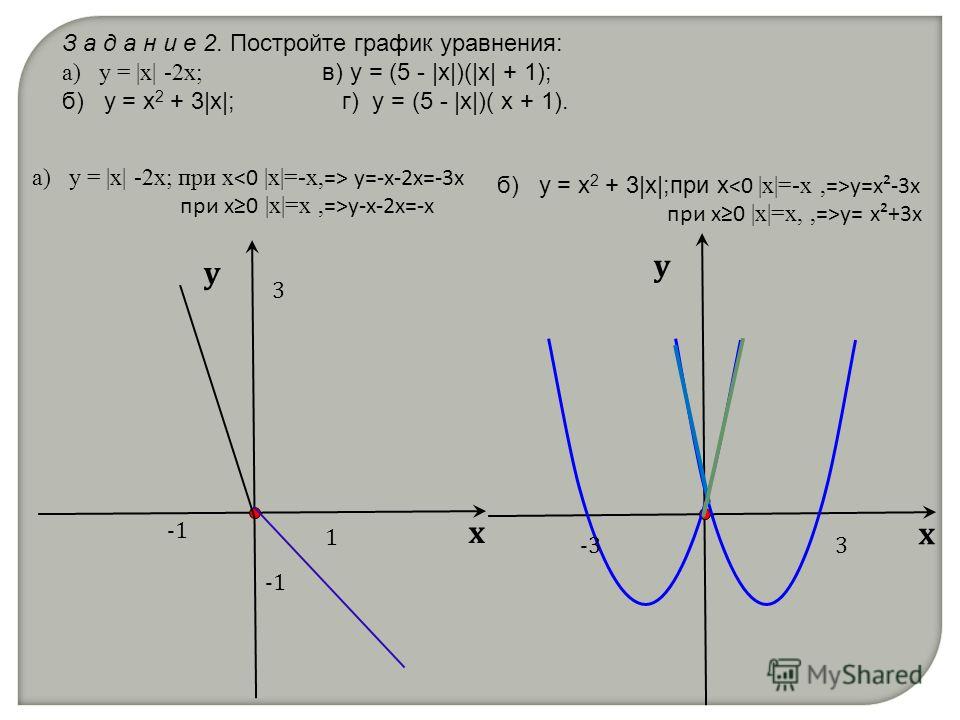
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
1) функции одной переменной;
2) функции трёх переменных в нашем случае.
Рассматривая функцию одной переменной, мы выяснили, что на оси Oy
отображается приращение функции f(x), соответствующее приращению
аргумента x. Если мы имеем дело с функцией трёх переменных, то приращения
аргументов x, y, z
отображаются на осях Оx, Оy, Оz. Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче .
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
1) функцию u = f(M), определённую в окрестности точки M с координатами x, y, z;
2) произвольный вектор l с направляющими косинусами
cosα, cosβ, cosγ.
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l. На получившейся прямой отметим точку M1, координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:
Величину отрезка MM1 можно обозначить .
Функция u = f(M) при этом получит приращение
.
Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть
.Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
.
Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.
Пример 1. Найти производную функции в точке M0(1; 2; 3) по направлению вектора .
Решение. Найдём частные производные функции в точке M0:
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
Следовательно,
Теперь можем найти производную по направлению данной функции по её формуле:
А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько
иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Так что придётся вновь повторить векторную алгебру.
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции в точке M0(1; 1; 1) по направлению вектора .
Решение. Найдём направляющие косинусы вектора
Найдём частные производные функции в точке M0:
Следовательно, можем найти производную по направлению данной функции по её формуле:
.
Градиент функции нескольких переменных в точке M0
характеризует направление максимального роста этой функции в точке M0 и
величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
.
Пример 4. Найти градиент функции в точке M0(2; 4;).
Решение. Найдём частные производные функции в точке M0:
Следовательно, можем записать искомый градиент данной функции:
.
Поделиться с друзьями
Производные
Функции нескольких переменных
x | y = x2 | (x,y) |
0 | 0 | (0,0) |
1 | 1 | (1,1) |
2 | 4 | (2,4) |
3 | 9 | (3,9) |
-1 | 1 | (-1,1) |
-2 | 4 | (-2,4) |
-3 | 9 | (-3,9) |
X | y=1/x | (x,y) |
1/3 | 3 | (1/3,3) |
1/2 | 2 | (1/2,2) |
1 | 1 | (1 ,1) |
2 | 1/2 | (2,1/2) |
3 | 1/3 | (3,1/3) |
-1/3 | -3 | (-1/3 , -3) |
-1/2 | -2 | (-1/2 , -2) |
-1 | -1 | (-1 , -1) |
-2 | -1/2 | (-2, -1/2) |
-3 | -1/3 | (-3,-1/3) |
| |x| = | x если x ≥ 0, т.e. x — не отрицательно -x если x |
График совпадает с линией y = x для x> 0 и с линией y = -x
для x < 0 .
graph of f(x) = -x
Соединяя эти два графика, мы получаем
график f(x) = |x|
Пример 3. Постройте график
t(x) = (x2— 4)/(x — 2) =
= ((x — 2)(x + 2)/(x — 2)) =
= (x + 2) x ≠ 2
Следовательно, эта функция может быть записана в виде
y = x + 2 x ≠ 2
График h(x)= x2 — 4 Or x — 2
график y = x + 2 x ≠ 2
Пример 4. Постройте график
| g(x) = | 1 если x ≤ 2 x + 2 если x > 2 |
Графики функций с перемещением
— Предположим, что график функции f(x) известен
— Тогда мы можем найти графики
y = f(x) + c
y = f(x) — c
y = f(x + c)
y = f(x — c)
y = f(x) + c — график функции f(x), перемещённый
ВВЕРХ на c значений
y = f(x) — c — график функции f(x), перемещённый
ВНИЗ на c значений
y = f(x + c) — график функции f(x), перемещённый
ВЛЕВО на c значений
y = f(x — c) — график функции f(x), перемещённый
Вправо на c значений
Пример 5.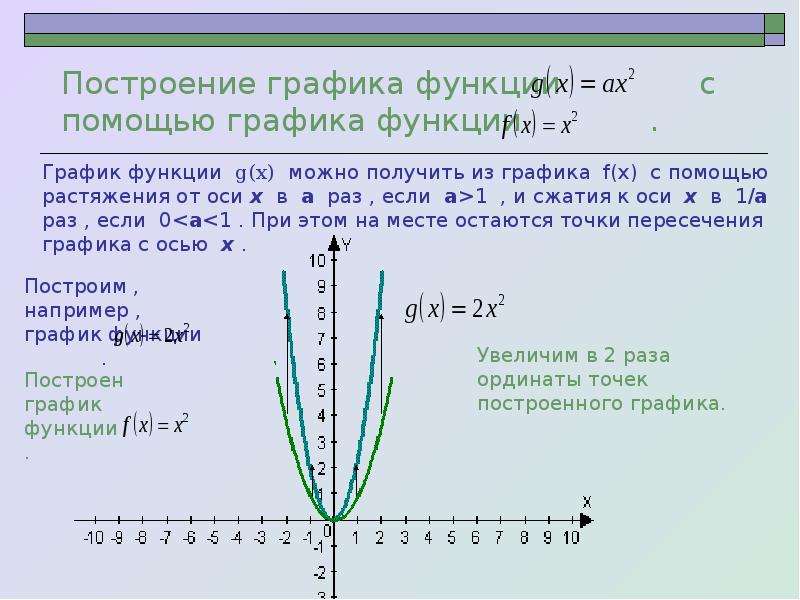 Постройте
Постройте
график y = f(x) = |x — 3| + 2
Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график
y = |x-3|
Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2
Пример 8
Постройте график
y = x2 — 4x + 5
Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:
y + 4 = (x2 — 4x + 5) + 4 y = (x2 — 4x + 4) + 5 — 4
y = (x — 2)2 + 1
Здесь мы видим, что этот график может быть получен перемещением графика y = x2 вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.
y = x2 — 4x + 5
Отражения
(-x, y) есть отражением (x, y) относительно оси y
(x, -y) есть отражением (x, y) относительно оси x
Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y
Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x
График может быть получен отражением и перемещением:
— Нарисуйте график
— Найдём его отражение относительно оси y, и получим график
— Переместим этот график вправо на 2 значения и получим график
Вот искомый график
Если f(x) умножена на положительною постояную c, то
график f(x) сжимается по вертикали, если 0 < c < 1
график f(x) растягивается по вертикали, если c > 1
Кривая не является графиком y = f(x) для любой функции f
Online 3-D Function Grapher
Версия автономного приложения этой программы построения трехмерных графиков, написанная на Flash Actionscript, намного быстрее, значительно расширяет возможности, встроенный калькулятор функций и многое другое . ..
..
Этот инструмент отображает z = f (x, y) математические функции в 3D. Это больше поход, чем инструмент. Для всех функций можно установить разные границы для x, y и z, чтобы получить максимальное удовольствие от просмотра.
Этот инструмент выглядит действительно великолепно с очень высоким уровнем детализации, но вам может быть удобнее использовать меньше деталей, если вы хотите вращать модель.
Примеры, Поддерживаемые функции, Добавить на свой сайт,
BBCODE для форумов
Если вам известна действительно крутая 3D-функция, которую вы хотели бы мне прислать, я мог бы добавить ее сюда и представить как кривую 3D-поверхности месяца.
Оси X, Y и Z показаны только для иллюстрации. Математики поменяли бы оси Y и Z друг с другом. У людей, занимающихся компьютерной графикой, по крайней мере одна из осей должна указывать в другом направлении, от вас.
Этот инструмент построения графиков поддерживает эти функции
sin (), cos (), tan (), asin (), acos (), atan ()
ln () — стандартный натуральный логарифмический
e — естественная основа
sqrt () — квадратный корень
abs () — абсолютное значение
max () — максимум из двух чисел
min () — минимум из двух чисел
floor () — ближайшее ближайшее целое число
ceil () — следующее ближайшее целое число
round () — ближайшее целое число
Покажите этот график на своем веб-сайте.
 2)
2) (05) cos (abs (x) + abs (y))
(06) cos (abs (x) + abs (y)) * (abs (x) + abs (y))
Контур XYZ СводкаИз этого туториала Вы узнаете, как создать контур из данных XYZ и добавить границы X и Y. Требуется минимальная исходная версия: 2020
Что вы узнаетеИз этого туториала Вы узнаете, как
Ступеньки Этот учебник связан со встроенным графическим образцом Contour Plots — XYZ Contour .
|
Как построить график данных XYZ в 3D в Microsoft Excel
Пару лет назад мы опубликовали сообщение в блоге о том, как графически отображать данные XYZ в MESH внутри Excel, Как графически отображать данные XYZ в MESH в Microsoft Excel . Сегодня мы хотели бы продолжить этот пост и объяснить различные варианты построения графиков данных XYZ в 3D в Excel; со сторонними приложениями и самостоятельно.
Сегодня мы хотели бы продолжить этот пост и объяснить различные варианты построения графиков данных XYZ в 3D в Excel; со сторонними приложениями и самостоятельно.Во-первых, знайте, что Microsoft Excel, хотя и является прекрасным приложением для работы с электронными таблицами, не предлагает удобных для пользователя вариантов построения графиков для чего-либо, кроме стандартных графиков. Это не значит, что Excel не может обрабатывать сложные графики, Excel определенно может, но это непросто. Однако есть несколько приложений, которые делают эту задачу чрезвычайно простой. Конечно, мы рассмотрим эти продукты, а также наиболее экономичным методом — сделаем это самостоятельно.
Как построить данные XYZ в 3D — линия, сплайн и разброс
Метод 1: Нанесение — Cel Tools В настоящее время самый простой способ взять данные XYZ и построить трехмерный график с вращением и масштабированием — это надстройка Excel, Cel Tools . Cel Tools — это набор инструментов, полный функций, которые упрощают работу с Excel обычным пользователям. Такие функции, как скрытие и защита содержимого паролем, изменение порядка списков, отправка электронных таблиц или книг, экспорт страниц, случайный выбор и многие другие. Интересующая нас функция находится в разделе графиков Cel Tools.
Cel Tools — это набор инструментов, полный функций, которые упрощают работу с Excel обычным пользователям. Такие функции, как скрытие и защита содержимого паролем, изменение порядка списков, отправка электронных таблиц или книг, экспорт страниц, случайный выбор и многие другие. Интересующая нас функция находится в разделе графиков Cel Tools.
На вкладке построения графиков в инструментах ячеек вы найдете множество вариантов построения графиков. Мы сосредоточимся на разделе «Инструменты 3D XYZ». Эта надстройка упрощает построение трехмерных графиков данных: выберите, нажмите «3D-линия», «3D-сплайн» или «3D-разброс», и график будет создан.
Cel Tools выполняет вычисления на основе выбранных данных XYZ, полос прокрутки для настройки поворота по оси X, поворота по оси Y, масштабирования и панорамирования и, наконец, отображает их в виде четкой диаграммы, которую вы можете настроить в соответствии с вашими потребностями. Еще одна замечательная особенность этого — возможность отправить свой график кому угодно. Поскольку все это содержится в документе Excel, вы можете отправить этот документ по электронной почте любому, у кого есть Excel, и они смогут вращать, масштабировать и панорамировать так же, как вы можете с Cel Tools.
Поскольку все это содержится в документе Excel, вы можете отправить этот документ по электронной почте любому, у кого есть Excel, и они смогут вращать, масштабировать и панорамировать так же, как вы можете с Cel Tools.
Этот метод очень сложен, и мы кратко объясним его сложности.Проще говоря, нам совсем не хочется воссоздавать колесо. Джордж Лунгу проделал потрясающую работу, объяснив математические уравнения, лежащие в основе построения трехмерных графиков в Microsoft Excel. Он предлагает множество руководств по этому поводу, и мы настоятельно рекомендуем вам посетить его страницу, если вы заинтересованы в создании потрясающих графиков с помощью Excel; Excel Необычное .
Существует несколько различных уравнений, которые необходимы для построения графика данных XYZ в Excel. Excel может отображать только две точки данных одновременно (X и Y).Поэтому вам нужно преобразовать XYZ только в XY. Это сложная часть, и уравнение показано справа:
Это сложная часть, и уравнение показано справа:
С помощью приведенных выше уравнений вы можете изобразить значения XYZ на двухмерном графике по осям X и Y. Необходимые числа — это ваши исходные значения X, Y и Z (OX, OY, OZ), азимут (вращение по оси X) и высота ( Вращение по оси Y). После того, как ваши формулы размещены, вы регулируете вращение и наблюдаете, как графические значения X и Y автоматически обновляются.
Опять же, не так просто и ясно, как с Cel Tools, но это действительно работает. И снова привет Джорджу Лунгу за формулы.
Данные XYZ, преобразованные в данные XY для расчетов трехмерных графиков
Высота = градусы поворота от 1 до 360 (Y)
Азимут = градусы поворота от 1 до 360 (X)
АЛЬФА = (3,1415926535 / 180) * Азимут
БЕТА = (3,1415926535 / 180) * Высота
OX = (Исходные значения Z)
OY = (исходные значения Y)
OZ = (Исходные значения Z)
Xr = Знак (OY) * Sin (ATan (OX / OY) + ALPHA) * SQRT (OY ^ 2 + OX ^ 2) [<- это то, что вы изображаете]
Yr = Знак (XXX) * Cos (ATan (OZ / XXX) + BETA) * SQRT (XXX ^ 2 + OZ ^ 2) [<- это то, что вы видите на графике]
XXX = Знак (OY) * COS (Atan (OX / OY) + ALPHA) * SQRT (OY ^ 2 + OX ^ 2)
(приведенные выше уравнения были изменены из связанной загрузки документа Excel Необычный URL-адрес XLS)youtube.com/embed/qNzLpAW_GeQ?autohide=2&autoplay=0&mute=0&controls=1&fs=1&loop=0&modestbranding=0&rel=1&showinfo=1&theme=dark&wmode=&playsinline=0″ frameborder=»0″ allowfullscreen=»» allow=»autoplay; encrypted-media; picture-in-picture» title=»»/>
Как построить данные XYZ в 3D — MESH, Surface Plot, Wireframe, Grid Frame
Теперь мы вернемся к нашему предыдущему посту о , как построить графики 3D MESH в Excel с использованием данных XYZ .Если вы пропустили эту статью, вы можете посетить ее по ссылке (-ам), доступной здесь, но я кратко подведу итог этой публикации.
Проще говоря, очень легко создать чертеж MESH в 3D, используя только значения XYZ. Однако это чрезвычайно утомительно, если вы не используете помощь форматированного расчета для размещения и усреднения точек. Как и раньше, я покажу вам два метода. Во-первых, стороннее приложение, а во-вторых, метод, который вы можете сделать самостоятельно.
Метод 1: Нанесение — XYZ Mesh Существует несколько методов преобразования XYZ в макет MESH, который может читать Excel, однако доступна только одна программа, которая преобразует эти данные в правильный макет. и заполняют пустые точки данных.Этот метод заполнения недостающих данных называется изгибом. Изгиб — это очень сложная цепочка вычислений, которые усредняют переменные по расстояниям и создают среднюю кривую в значениях, зависящих от расстояния. По сути, он делает расчетное предположение относительно того, какие числа должны быть в этой недостающей точке данных.
Почему недостающие точки данных представляют собой такую большую проблему? Microsoft Excel выглядит как эти пустые точки данных как данные, а не как отсутствующие значения. Это означает, что вместо того, чтобы просто пропускать эти значения (как это делают большинство графических движков), Excel считает их нулями «0», а взамен вводит ложные данные в графическое изображение.
XYZ Mesh в настоящее время является единственным доступным программным обеспечением, которое принимает данные XYZ и конвертирует их непосредственно в формат Excel MESH с кривыми данных. Просто вставьте свои значения в соответствующие столбцы X, Y и Z, выберите настройки и нажмите «преобразовать».
В мгновение ока данные преобразуются и отображаются в окне предварительного просмотра, отображая каркасную сетку преобразованных данных. Отсюда данные можно экспортировать в Excel. Быстрое и легкое преобразование с помощью изгиба и отсутствие хлопот, связанных со следующей частью этого поста….
Как упоминалось ранее, Excel имеет неприятную привычку думать, что никакие значения не могут быть равны нулю. Хотя в некоторых случаях это может быть правдой (где ноль ничего не значит), что касается чисел, ноль является действительным числом. Это может привести к неправильному отображению данных, поэтому использование XYZ Mesh очень важно для создания гладких данных.
Но это раздел, в котором мы учим вас делать это самостоятельно.Первое, что вам нужно понять, это то, что данные XYZ отображаются в трех столбцах: X, Y и Z. Чтобы Excel смог отобразить это на графике 3D Surface, данные должны быть в формате MESH. Формат MESH — это структура, которая содержит строки и столбцы, очень похожая на электронную таблицу. Значения X устанавливаются стационарно в первом столбце каждой строки, значения Y устанавливаются стационарно в первой строке каждого столбца, а значения Z размещаются точно там, где X означает Y для соответствующего значения Z. Чтобы лучше понять это, посмотрите изображение, представленное ниже:
Чтобы лучше понять это, посмотрите изображение, представленное ниже:
Как показано на изображении выше, значения X и Y достаточно легко разместить, однако значения Z потребуют времени.Причина в том, что вам нужно будет отслеживать и вставлять каждое отдельное значение Z в нужное место, чтобы правильно построить этот график формата MESH. Но подождите, это была легкая часть. Далее следует вызов. Вам необходимо рассчитать разницу между значениями, чтобы получить правильное искривление данных. Если вы пропустите эту часть, Excel будет считать, что ваши пустые точки данных равны нулю, и ваш график будет выглядеть следующим образом (изображение справа ->). Что, если вы не можете сказать, неверно.
Расчет для данных кривой в MESH
Существует несколько различных способов расчета разницы между значениями и расстояниями, но все они имеют одинаковый процесс.- Выберите метод расчета, который вам нравится; Я лично предпочитаю метод VALUE = A [+/-] ((B — A) / C ).

- Поместите вычисление в пустую ячейку.
- Перетаскивайте, пока не дойдете до следующего значения.
Это может показаться простым, но требует очень много времени, и если у вас нет точных расчетов, график будет неправильным.
К сожалению, нет другого способа сформулировать, скопировать и вставить эти значения самостоятельно, если вы не используете стороннее приложение.Если вы решите использовать стороннее приложение для упрощения процесса, знайте, что есть несколько доступных вариантов. Некоторые конвертируют XYZ в MESH, а другие берут данные MESH и заполняют пустые точки данных. Если вы идете по этому пути, почему бы не использовать приложение, которое будет и то, и другое? Сетка XYZ .
Надеюсь, этот пост был вам полезен. Если вы хотите поговорить с нами о своих чувствах к этому посту, оставьте комментарий внизу. Нам нравится получать известия от наших читателей!
Связанные3d Graph Xyz Online
Разместите свои комментарии?
Math4d: Онлайн-калькулятор для построения трехмерных графиков
3 часа назад Интерактивный калькулятор для построения трехмерных графиков в вашем браузере. Рисуйте, анимируйте и делитесь поверхностями, кривыми, точками, линиями и векторами. Math4d: Онлайн-3D-графика Калькулятор
Рисуйте, анимируйте и делитесь поверхностями, кривыми, точками, линиями и векторами. Math4d: Онлайн-3D-графика Калькулятор
Веб-сайт: https://www.math4d.org/
Категория : Используйте слова в предложении
3d
3D Grapher14 intmath.com 903
6 часов назад 3D и Contour Grapher . График в 3 измерениях в общем записывается: z = f (x, y), то есть значение z находится путем подстановки как значения x, так и значения y.. Первый пример, который мы видим ниже, — это график z = sin (x) + sin (y). Это функция от x и y. Вы можете использовать следующий апплет для изучения трехмерных графиков и даже создания своих собственных , используя переменные x и y.
Веб-сайт: https://www.intmath.com/vectors/3d-grapher.php
Категория : Используйте слова в предложении
3d
3D Vector Plotter Academo.
 org Бесплатно , интерактивный
org Бесплатно , интерактивный4 часа назад 3D Векторный плоттер.Интерактивный сюжет из 3D векторов. Посмотрите, как два вектора связаны с их результирующим, разностным и перекрестным произведением. Maths Geometry Graph — вектор построения графика. Приведенная выше демонстрация позволяет вам ввести до трех векторов в форме (x, y, z). Нажатие кнопки рисования отобразит векторы на диаграмме (масштаб диаграммы будет
Веб-сайт: https://academo.org/demos/3d-vector-plotter/
Категория : Используйте слова в предложении
3d
XYZ 3D Mesh Surface Plotter
5 часов назад 1.Обзор XYZ -Plot — это плоттер данных общего назначения 3D -данных, который отображает трехмерные данные в виде трехмерной сетки поверхности. XYZ -Plot предоставляет интерактивные кнопки для поворота перспективы просмотра, печати и выбора других параметров отображения.
Веб-сайт: http://www.csim.com/xgraph/xyz.html
Категория : Используйте слова в предложении
3d
Онлайн-калькулятор: системы координат 3d
8 ч. назад Эта система координат определяет точку в пространстве 3d с радиусом r, азимутальным углом φ и высотой z.Высота z напрямую соответствует координате z в декартовой системе координат. Радиус r — положительное число, кратчайшее расстояние между точкой и осью z. Азимутальный угол φ — это значение угла в диапазоне 0..360.
Веб-сайт: https://planetcalc.com/7952/
Категория : используйте слова в предложении
3d
Создайте трехмерный поверхностный график в Интернете с помощью Chart Studio и Excel
4 ч. назад Выберите « 3D Surface Plot» с помощью кнопки MAKE A PLOT в строке меню. Выберите форму ввода как «Z-матрица», нажмите кнопку «Выбрать все столбцы». Если эти параметры включены, нажмите кнопку графика, чтобы создать диаграмму. Шаг 4.
Выберите форму ввода как «Z-матрица», нажмите кнопку «Выбрать все столбцы». Если эти параметры включены, нажмите кнопку графика, чтобы создать диаграмму. Шаг 4.
Веб-сайт: https://plotly.com/chart-studio-help/excel/3d-surface/
Категория : Используйте a в предложении
3d
3D График XYZ в Excel Maclab.sk
Just Now Как создать 3D диаграммы и координаты XYZ в Excel. Excel — это приложение для работы с электронными таблицами, которое может отображать данные, рассчитанные с использованием 2D-диаграмм.Под термином 2D график я подразумеваю систему координат x, y. Визуализация координат пространственных данных x, y, z с помощью 3D-графика не позволяет даже последняя версия (написана в 2016 году). То, что Excel представляет собой трехмерный график , на самом деле всего лишь маленький…
Веб-сайт: https://www. maclab.sk/clanky/en-3d-graph-excel.php
maclab.sk/clanky/en-3d-graph-excel.php
Категория : использовать в предложении
3d
3D точечная диаграмма Highcharts.com
2 часа назад 3D точечная диаграмма. Перетаскиваемый ящик. Диаграмма со 100 точками данных. Щелкните и перетащите область графика, чтобы вращать ее в пространстве. Диаграмма, демонстрирующая диаграмму рассеяния 3D , на которой диаграмму можно вращать для просмотра точек под разными углами. Каждая точка имеет значения координат x, y и z. Просмотр в виде таблицы данных, перетаскиваемое поле. На диаграмме есть 1 ось X, отображающая значения.
Веб-сайт: https://www.highcharts.com/demo/3d-scatter-draggable
Категория : Используйте слова в предложении
3d
в кубической форме.xyz Инструмент для создания 3D-схем Minecraft Build Edit
Just Now Cubical — это самый продвинутый онлайн-редактор , создатель и просмотрщик проектов и сборок, совместимых с Minecraft. Приведенный ниже список — это лишь некоторые из множества вариантов, которые он может предложить. Особенности: Игра нравится — элементы управления, движение, обнаружение ударов и другие функции позволяют почувствовать себя комфортно в игре, а не техническим редактором.
Приведенный ниже список — это лишь некоторые из множества вариантов, которые он может предложить. Особенности: Игра нравится — элементы управления, движение, обнаружение ударов и другие функции позволяют почувствовать себя комфортно в игре, а не техническим редактором.
Веб-сайт: https://cubical.xyz/
Категория : Используйте слова в предложении
12 Лучшее бесплатное программное обеспечение для построения трехмерных графиков для Windows
6 часов назад Microsoft Mathematics — популярное программное обеспечение для вычислений и программное обеспечение для построения графиков 2D и 3D для Windows.В разделе Graphing вы можете строить уравнения и функции, наборы данных, параметрические и неравенства. Он поддерживает декартову, сферическую и цилиндрическую системы координат. Не один, с его помощью можно строить сразу несколько функций. Он предоставляет некоторые элементы управления graph , с помощью которых вы…
Веб-сайт: https://listoffreeware. com/best-free-3d-graphing-software-windows/
com/best-free-3d-graphing-software-windows/
Категория : Используйте слова в предложение
3d
Справка Интерактивные учебные пособия Основы трехмерного построения
7 часов назад Нажмите OK, чтобы преобразовать данные XYZ в матрицу.Активируйте матрицу и выберите Plot> 3D : 3D Colormap Surface, чтобы создать еще один 3D-график , говорит Graph3. Вернитесь к Graph2, щелкните правой кнопкой мыши любое пустое пространство в рамке слоя, чтобы выбрать «Копировать формат: все форматы стилей» в контекстном меню.
Веб-сайт: https://www.originlab.com/doc/Tutorials/3D-Plotting-Basic
Категория : Используйте слова в предложении
3d
Calculus III 3D Coordinate Система
1 час назад Итак, в трехмерной системе координат это плоскость, которая будет параллельна плоскости yzyz и пройдет через ось xx в точке x = 3 x = 3.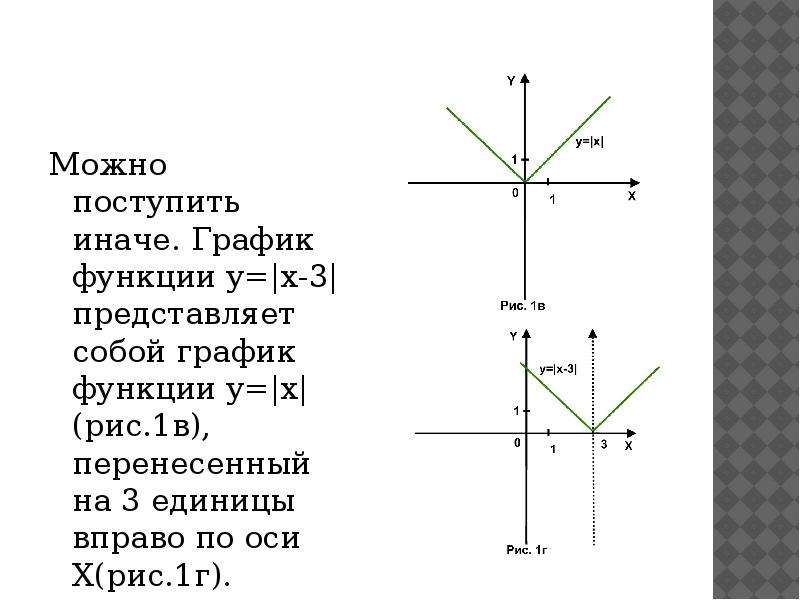 Вот график для x = 3 x = 3 в R R. Вот график для x = 3 x = 3 в R 2 R 2. Наконец, вот график для x = 3 x = 3 в R 3 R 3.
Вот график для x = 3 x = 3 в R R. Вот график для x = 3 x = 3 в R 2 R 2. Наконец, вот график для x = 3 x = 3 в R 3 R 3.
Веб-сайт: https://tutorial.math.lamar.edu/Classes/CalcIII/3DCoords.aspx
Категория : Используйте слова в предложении
XYZ2WF XGRAPH Универсальная утилита для построения 2D-графиков
3 часа назад XYZ -2-WF — это универсальная утилита для преобразования необработанных файлов трехмерных числовых данных, таких как вещественные матрицы, в формат WFL для отображения в WinFrame3D.Полученные в результате 3D-графики можно интерактивно вращать и просматривать с произвольных точек зрения в режиме реального времени.
Веб-сайт: http://www.xgraph.org/xyz2wf.html
Категория : Используйте слова в предложении
3d
3D-график в Excel Как создать 3D-график поверхности ( Диаграмма
8 часов назад На графике поверхности Excel 3D вращение 3D необходимо отрегулировать в соответствии с диапазоном данных, так как его может быть сложно прочитать с диаграммы, если перспектива неправильная. Ось должна быть…
Ось должна быть…
2 . Выберите данные, в которых мы хотим построить трехмерную диаграмму.
3 . Теперь на вкладке «Вставка» в разделе диаграмм щелкните поверхностную диаграмму.
4 . Типичный трехмерный график поверхности в Excel показан ниже, но на данный момент мы не можем многое прочитать из этого графика.
Веб-сайт: https://www.wallstreetmojo.com/3d-plot-in-excel/
Категория : использовать в предложении
3d
График разброса 3D в Excel Как сделать Создание точечной диаграммы 3D
8 часов назад Как создать точечную диаграмму 3D в Excel? Что такое 3D точечная диаграмма в Excel? Диаграмма рассеяния — это график или диаграмма, используемая для визуализации и интерпретации данных с использованием точек для представления значений двух разных переменных: одна отображается по оси x (горизонтальная ось), а другие — по оси y (вертикальная ось).
Веб-сайт: https://www.educba.com/3d-scatter-plot-in-excel/
Категория : Использование в предложении
3d
Графический калькулятор Runiter 3D Windows, Mac, Linux
Just Now Постройте математические уравнения и точки разброса с помощью этого мощного программного обеспечения. Высококачественные графики строятся быстро и в реальном времени. Может быть установлен на любой компьютер с ОС Windows, Mac или Linux. Постройте любое неявное или явное уравнение в 2D или 3D .Поддерживаемые координаты…
Веб-сайт: https://runiter.com/graphing-calculator/
Категория : Используйте слова в предложении
3d
3D Functions Plotter Графики двух переменных функций и
8 часов назад Funcions 3D плоттер вычисляет аналитический и числовой интеграл, а также вычисляет частные производные по x и y для 2 переменных функций. Введите интервал для переменной x для переменной и плоттера и 3D Функции График функции в пространстве.В резюме, это приложение функции grapher .
Введите интервал для переменной x для переменной и плоттера и 3D Функции График функции в пространстве.В резюме, это приложение функции grapher .
Веб-сайт: http://www.mathstools.com/section/main/3DFunctions_Plotter
Категория : использовать и в предложении
3d
Надстройки для трехмерного моделирования ThreeDify
для инструментов Microsoft Office Just Now 3D Надстройки для Microsoft Word, Excel и PowerPoint Надстройки 3D от ThreeDify для Microsoft Word, Excel и PowerPoint предоставляют пользователям Microsoft Office непревзойденный графический интерфейс , просмотр моделей и возможности совместной работы.Excel Grapher Excel Grapher — это инновационный инструмент 3D / 4D для построения графиков и диаграмм, развернутый как надстройка для Microsoft Excel®. Дополнительная информация XLCurvFit XLCurvFit…
Дополнительная информация XLCurvFit XLCurvFit…
Веб-сайт: https://3dexcel.com/
Категория : Используйте for в предложении
3d
Трехмерное построение графика в Python 4 914 часов назад Как и двухмерный график
, мы можем использовать разные способы представления трехмерного графика .Мы можем сделать точечный график, контурный график, поверхностный график и т. Д. Давайте посмотрим на разные трехмерные графики. Построение трехмерных линий и точек. График с линиями и точками представляет собой простейший трехмерный график . ax.plot3d и ax.scatter — это функции для построения графика линии и точкиВеб-сайт: https://www.geeksforgeeks.org/three-dimensional-plotting-in-python-using-matplotlib/
Категория : Использование в предложении
Трехмерный калькулятор средней точки Бесплатные онлайн-калькуляторы
4 часа назад Формула средней точки 3D . (x1 + x2 / 2, y1 + y2 / 2, z1 + z2 / 2) 3D Калькулятор средней точки , используемый для нахождения средней точки вектора 3d . Средняя точка делит отрезок линии на два равных отрезка. Средняя точка трех измерений вычисляется по средним точкам координат x, y и z и разделяется на значения x1, y1, z1 и x2, y2, z2. Чтобы найти середину прямой
(x1 + x2 / 2, y1 + y2 / 2, z1 + z2 / 2) 3D Калькулятор средней точки , используемый для нахождения средней точки вектора 3d . Средняя точка делит отрезок линии на два равных отрезка. Средняя точка трех измерений вычисляется по средним точкам координат x, y и z и разделяется на значения x1, y1, z1 и x2, y2, z2. Чтобы найти середину прямой
Веб-сайт: https://www.meracalculator.com/graphic/3dimensional-midpoint.php
Категория : Используйте слова в предложении
3d
XYZ Столбчатые диаграммы Справка Grapher
5 часов назад Нажмите кнопку XYZ Vertical Bar Chart или XYZ Horizontal Bar Chart, чтобы создать горизонтальную или вертикальную столбчатую диаграмму 3D из 3 переменных. 3D XYZ гистограммы показывают. Переменные X, Y и Z. Полосы могут отображаться вертикально или горизонтально. Обсуждение гистограммы предполагает наличие горизонтальной гистограммы; поменяйте местами X и Y для вертикальной гистограммы.
Обсуждение гистограммы предполагает наличие горизонтальной гистограммы; поменяйте местами X и Y для вертикальной гистограммы.
Веб-сайт: http://grapherhelp.goldensoftware.com/Graphs/3D_XYZ_Bar_Chart.htm
Категория : Используйте слова в предложении
3D-график в режиме онлайн
Создайте 3D-график в 3D-графике. и Excel
7 часов назад Создание точечной диаграммы.Выберите « 3D Scatter Plots» с помощью кнопки MAKE A PLOT в строке меню. Включите параметр «Группировать по» на панели инструментов и выберите заголовки, как показано на рисунке. Наконец, нажмите кнопку графика, чтобы сгенерировать график. Шаг 4.
Веб-сайт: http://plotly.github.io/excel/3d-scatter-plots/
Категория : Используйте a в предложении
3d
Основы осциллографа | Руководство по чтению и эксплуатации
Типы волн
Большинство волн можно разделить на следующие типы:
- Синусоидальные волны.

- Квадратные и прямоугольные волны.
- Пилообразные и треугольные волны.
- Форма ступеней и импульсов.
- Периодические и непериодические сигналы.
- Синхронные и асинхронные сигналы.
- Сложные волны.
Далее мы рассмотрим каждый из этих типов волн.
Синусоидальные волны
Синусоидальная волна является основной формой волны по нескольким причинам. Он обладает гармоничными математическими свойствами »- это та же форма синуса, которую вы, возможно, изучали на уроках тригонометрии.
Напряжение в розетке изменяется синусоидально. Тестовые сигналы, создаваемые осцилляторной схемой генератора сигналов, часто являются синусоидальными волнами.
Большинство источников питания переменного тока генерируют синусоидальные волны (переменный ток означает переменный ток, хотя и переменное напряжение; постоянный ток означает постоянный ток, что означает постоянный ток и напряжение, которое производит батарея. ) Затухающая синусоида — это особый случай, когда вы может видеть в цепи, которая колеблется, но со временем стихает.
) Затухающая синусоида — это особый случай, когда вы может видеть в цепи, которая колеблется, но со временем стихает.
Квадратные и прямоугольные волны
Прямоугольная волна — еще одна распространенная форма волны.По сути, прямоугольная волна — это напряжение, которое включается и выключается (или повышается и понижается) через определенные промежутки времени. Это стандартная волна для тестирования усилителей. Хорошие усилители увеличивают амплитуду прямоугольной волны с минимальными искажениями.
Телевидение, радио и компьютерные схемы часто используют прямоугольные волны для синхронизации сигналов. Прямоугольная волна похожа на прямоугольную, за исключением того, что высокие и низкие временные интервалы не имеют равной длины. Это особенно важно при анализе цифровых схем.
Пилообразные и треугольные волны
Пилообразные и треугольные волны возникают из-за схем, предназначенных для линейного управления напряжением, таких как горизонтальная развертка аналогового осциллографа или растровая развертка телевизора.
Переходы между уровнями напряжения этих волн изменяются с постоянной скоростью. Эти переходы называются рампами.
Формы ступеней и импульсов
Такие сигналы, как шаги и импульсы, которые возникают редко или непериодически, называются однократными или переходными сигналами.
Шаг указывает на внезапное изменение напряжения, подобное изменению напряжения, которое вы видите, если вы включаете выключатель питания.
Импульс указывает на внезапные изменения напряжения, похожие на изменения напряжения, которые вы видите, если вы включите, а затем снова выключите питание. Импульс может представлять один бит информации, проходящий через компьютерную схему, или это может быть сбой или дефект в цепи.
Набор распространяющихся вместе импульсов создает последовательность импульсов. Цифровые компоненты в компьютере взаимодействуют друг с другом с помощью импульсов.Эти импульсы могут быть в форме последовательного потока данных, или несколько сигнальных линий могут использоваться для представления значения на параллельной шине данных. Импульсы также распространены в рентгеновском, радиолокационном и коммуникационном оборудовании.
Импульсы также распространены в рентгеновском, радиолокационном и коммуникационном оборудовании.
Периодические и непериодические сигналы
Повторяющиеся сигналы называются периодическими сигналами, а сигналы, которые постоянно меняются, называются непериодическими сигналами. Неподвижное изображение аналогично периодическому сигналу, в то время как фильм аналогичен непериодическому сигналу.
Синхронные и асинхронные сигналы
Если между двумя сигналами существует временная зависимость, эти сигналы называются синхронными. Сигналы часов, данных и адреса внутри компьютера являются примерами синхронных сигналов.
Асинхронные сигналы — это сигналы, между которыми не существует временной зависимости. Поскольку не существует временной корреляции между касанием клавиши на клавиатуре компьютера и часами внутри компьютера, эти сигналы считаются асинхронными.
Сложные волны
Некоторые формы сигналов сочетают в себе характеристики синусов, квадратов, ступеней и импульсов для создания сигналов сложной формы. Информация о сигнале может быть встроена в виде изменений амплитуды, фазы и / или частоты.
Информация о сигнале может быть встроена в виде изменений амплитуды, фазы и / или частоты.
Например, хотя сигнал на рисунке 6 является обычным композитным видеосигналом, он состоит из множества циклов высокочастотных сигналов, встроенных в низкочастотную огибающую.
В этом примере важно понимать относительные уровни и временные отношения шагов.Для просмотра этого сигнала вам понадобится осциллограф, который фиксирует низкочастотную огибающую и смешивает высокочастотные волны с градацией интенсивности, чтобы вы могли видеть их общую комбинацию в виде изображения, которое можно интерпретировать визуально.
Осциллографы с цифровым люминофором (DPO) лучше всего подходят для просмотра сложных волн, таких как видеосигналы, показанные на рисунке 6. Их дисплеи предоставляют необходимую информацию о частоте появления или градацию интенсивности, которая необходима для понимания формы волны действительно делает.
Некоторые осциллографы могут отображать определенные типы сложных сигналов особым образом. Например, телекоммуникационные данные могут отображаться в виде глазковой диаграммы или диаграммы созвездия:
Например, телекоммуникационные данные могут отображаться в виде глазковой диаграммы или диаграммы созвездия:
Рисунок 6 : Составной видеосигнал NTSC является примером сложной волны.
Телекоммуникационные цифровые сигналы данных могут отображаться на осциллографе в виде сигнала особого типа, называемого глазковой диаграммой. Название происходит от сходства формы волны с серией глаз (рис. 7).
Глазковые диаграммы формируются, когда цифровые данные от приемника дискретизируются и применяются к вертикальному входу, в то время как скорость передачи данных используется для запуска горизонтальной развертки. Глазковая диаграмма отображает один бит или единичный интервал данных со всеми возможными краевыми переходами и состояниями, наложенными на одном всеобъемлющем представлении.
Диаграмма созвездия — это представление сигнала, модулированного схемой цифровой модуляции, такой как квадратурная амплитудная модуляция или фазовая манипуляция.
GRE Multiple-Choice — Выберите один вопрос (для тестируемых)
Если какое значение x?
- 4
- 7
- 12
Пояснение
Решая уравнение относительно x, вы получаете и поэтому Правильный ответ — вариант A,
Какое из следующих чисел дальше всего от цифры 1 в числовой строке?
- 0
- 5
- 10
Пояснение
Обвод каждого варианта ответа на схеме числовой прямой (рис. 4) показывает, что из данных чисел это наибольшее расстояние от 1.
4) показывает, что из данных чисел это наибольшее расстояние от 1.
Рисунок 4
Другой способ ответить на этот вопрос — вспомнить, что расстояние между двумя числами на числовой прямой равно абсолютному значению разницы двух чисел. Например, расстояние между и 1 равно, а расстояние между 10 и 1 равно. Правильный ответ — вариант А,
.Рисунок 5
На рисунке выше показан график функции f, определенной для всех чисел x.Для какой из следующих функций g, определенных для всех чисел x, график g пересекает график f?
Пояснение
Вы можете видеть, что все пять вариантов являются линейными функциями, графики которых представляют собой линии с различными наклонами и пересечениями по оси Y. График варианта A представляет собой линию с наклоном 1 и точкой пересечения по оси Y, показанной на рисунке 6.
Рисунок 6
Ясно, что эта линия не будет пересекать график f слева от оси y.Справа от оси y график f представляет собой линию с наклоном 2, который больше, чем наклон 1. Следовательно, по мере увеличения значения x значение y увеличивается для f быстрее, чем для g, и, следовательно, графики не пересекаются справа от оси y. Вариант B также исключен. Обратите внимание, что если бы точка пересечения по оси Y любой из линий в вариантах A и B была больше или равна 4, а не меньше 4, они пересекали бы график f.
Варианты C и D — это линии с наклоном 2 и пересечением по оси Y меньше 4.Следовательно, они параллельны графику f (справа от оси y) и, следовательно, не будут его пересекать. Любая линия с наклоном больше 2 и точкой пересечения по оси Y меньше 4, например линия в Варианте E, будет пересекать график f (справа от оси Y). Правильный ответ — выбор E,
.Автомобиль проехал 33 мили на галлон бензина по цене 2,95 доллара за галлон. Какова примерная стоимость в долларах бензина, использованного для езды на автомобиле 350 миль?
- $ 10
- $ 20
- $ 30
- $ 40
- $ 50
Пояснение
Просмотр вариантов ответа показывает, что вы можете сделать хотя бы некоторую оценку и при этом ответить уверенно.В машине использовались галлоны бензина, поэтому стоимость составляла доллары. Вы можете оценить продукт, оценив немного ниже, 10, и оценив 2,95, немного выше, 3, чтобы получить приблизительно доллары. Вы также можете использовать калькулятор, чтобы вычислить более точный ответ, а затем округлить ответ до ближайших 10 долларов в соответствии с вариантами ответов. Калькулятор вычисляет десятичную дробь, которая округляется до 30 долларов. Таким образом, правильный ответ — вариант C, 30 долларов.
В одной банке 60 мармеладов: 22 белых, 18 зеленых, 11 желтых, 5 красных и 4 фиолетовых.Если мармелад должен быть выбран наугад, какова вероятность того, что мармелад не будет ни красным, ни пурпурным?
- 0,09
- 0,15
- 0,54
- 0,85
- 0,91
Пояснение
Поскольку в банке 5 красных и 4 фиолетовых мармелада, 51 мармелад не является ни красным, ни пурпурным, и вероятность выбора одного из них равна. Поскольку все варианты ответов являются десятичными, вы должны преобразовать дробь в десятичную. эквивалент, 0.85. Таким образом, правильный ответ — вариант D, 0,85.
ПЕРЕСЕЧЕНИЕ
В этой статье описаны синтаксис формулы и использование функции ПЕРЕСЕЧЕНИЕ в Microsoft Excel.
Описание
Вычисляет точку, в которой линия будет пересекать ось Y, используя существующие значения x и y. Точка пересечения основана на наиболее подходящей линии регрессии, построенной через известные значения x и известные значения y.Используйте функцию ПЕРЕСЕЧЕНИЕ, если вы хотите определить значение зависимой переменной, когда независимая переменная равна 0 (нулю). Например, вы можете использовать функцию ПЕРЕСЕЧЕНИЕ, чтобы предсказать электрическое сопротивление металла при 0 ° C, когда ваши точки данных были сняты при комнатной температуре и выше.
Синтаксис
ПЕРЕСЕЧЕНИЕ (известные_y, известные_x)
Аргументы функции ПЕРЕСЕЧЕНИЕ следующие:
Замечания
Аргументы должны быть либо числами, либо именами, массивами или ссылками, содержащими числа.
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако ячейки с нулевым значением включены.
Если известные_y и известные_x содержат разное количество точек данных или не содержат точек данных, функция ПЕРЕСЕЧЕНИЕ возвращает значение ошибки # Н / Д.
Уравнение для пересечения линии регрессии a:
, где наклон b рассчитывается как:
, где x и y — это выборка, означает СРЕДНЕЕ (известные_x) и СРЕДНЕЕ (известные_y).
Базовый алгоритм, используемый в функциях ПЕРЕСЕЧЕНИЕ и НАКЛОН, отличается от базового алгоритма, используемого в функции ЛИНЕЙН. Разница между этими алгоритмами может привести к разным результатам, когда данные не определены и коллинеарны. Например, если точки данных аргумента known_y равны 0, а точки данных аргумента known_x равны 1:
INTERCEPT и SLOPE возвращают # DIV / 0! ошибка.Алгоритм ПЕРЕСЕЧЕНИЯ и НАКЛОНА предназначен для поиска одного и только одного ответа, и в этом случае может быть более одного ответа.
ЛИНЕЙН возвращает значение 0. Алгоритм ЛИНЕЙН предназначен для получения приемлемых результатов для коллинеарных данных, и в этом случае можно найти по крайней мере один ответ.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового листа Excel.Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите Enter. При необходимости вы можете настроить ширину столбца, чтобы увидеть все данные.
Известно | Известно x | |
2 | 6 | |
3 | 5 | |
9 | 11 | |
1 | 7 | |
8 | 5 | |
Формула | Описание | Результат |
= ПЕРЕСЕЧЕНИЕ (A2: A6, B2: B6) | Точка, в которой линия будет пересекать ось Y с использованием значений x и y выше | 0. |

 Например, различные точки построены на рисунке внизу.
Например, различные точки построены на рисунке внизу.
 Постройте график f(x) = |x|
Постройте график f(x) = |x|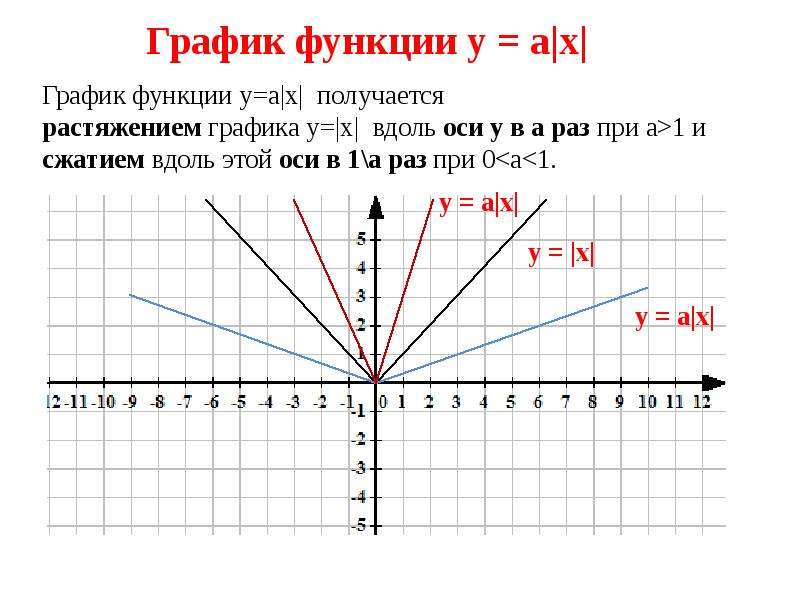

 Затем установите параметр сглаживания на 0,04
Затем установите параметр сглаживания на 0,04

Ваш комментарий будет первым