Построение графика функции по точкам. Практикум по математическому анализу. Урок 6
Наглядное графическое изображение функциональной зависимости между двумя переменными и можно получить, рассматривая значения этих переменных как координаты точек на плоскости.
Графиком функции, заданной уравнением , называется совокупность всех точек плоскости, координаты которых удовлетворяют этому уравнению.
Обычно график функции представляет некоторую плоскую линию.
Построение графика аналитически заданной функции по точкам выполняется в следующем порядке:
1) по данному аналитическому выражению функции составляется таблица соответствующих друг другу значений переменных;
2) выбирается система координат с подходящими единицами масштаба для каждой переменной.
Обычно применяется прямоугольная система координат и одна общая единица масштаба для обеих координатных осей;
3) строятся точки, координатами которых являются соответствующие друг другу значения аргумента и функции, содержащиеся в таблице;
4) полученные точки соединяются плавной линией.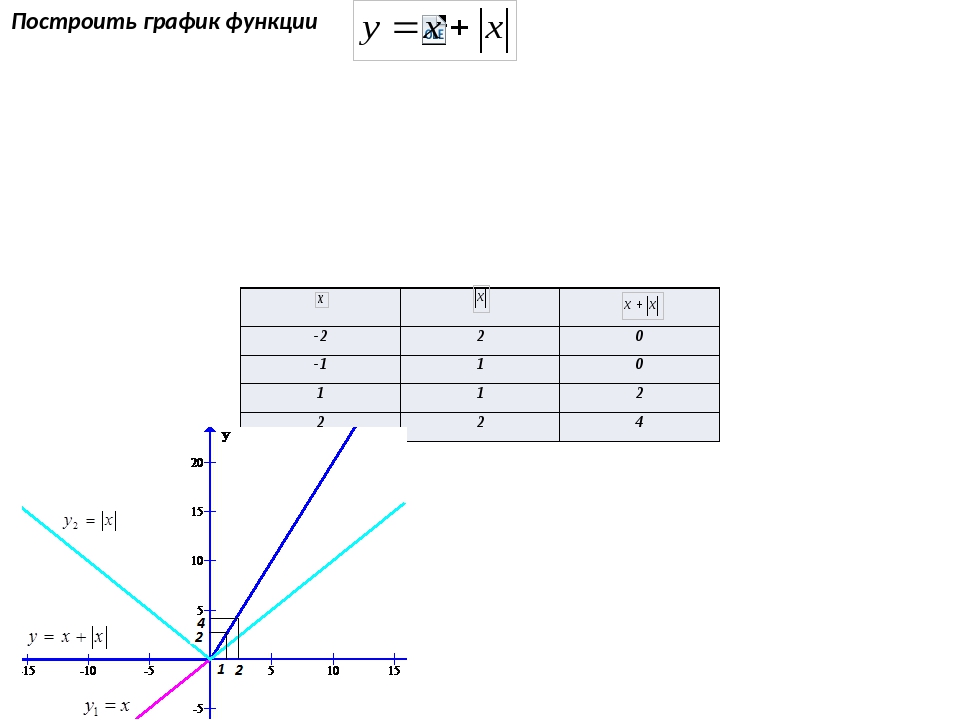
Построенный этим способом график функции будет тем точнее, чем больше значений переменных содержится в таблице, чем больше точек будет нанесено на координатную плоскость.
Построение графика функции упрощается, если она является четной, нечетной или периодической. График четной функции симметричен относительно оси ; график нечетной функции симметричен относительно начала координату график периодической функции получается путем повторения части ее графика, соответствующей одному периоду.
Пример 1. Построить графики функций:
1) на отрезке [—2; 4];
2) на отрезке [—5; 5];
3) на отрезке ;
4) на отрезке [-6; 5];
5) между точками пересечения с осью .
Решение. 1) В условии задачи указано, что независимой переменной можно придавать только значения, заключенные на отрезке [—2; 4]. Учитывая это, составим следующую таблицу, беря для простоты только целые значения и вычисляя из данного уравнения соответствующие значения :
Рис. 1
1
Введем прямоугольную систему координат, как показано на рис. 1, с одинаковыми единицами масштаба, которые указаны числовыми пометками на координатных осях.
Построим точки, откладывая содержащиеся в таблице значения аргумента по оси абсцисс, а значения функции по оси ординат. Соединим полученные точки плавной кривой, которая и будет графиком данной функции. Эта кривая называется параболой.
Вообще графиком всякой квадратной функции является парабола, ось симметрии которой параллельна оси .
2) Функция — нечетная, так как для нее . Для значений аргумента, отличающихся только по знаку, значения нечетной функции будут также отличаться только по знаку. Поэтому при составлении таблицы здесь достаточно вычислить изданного уравнения значения функции только для положительных значений аргумента. Значения функции для отрицательных значений аргумента получим путем простои перемены знаков.
Выберем систему координат с одинаковыми масштабами на координатных осях (рис.
 2).
2).Построим точки для каждой пары числовых значений и , которые содержатся в строках таблицы. Соединяя эти точки плавной кривой, получим график, симметричный относительно начала координат.
Рис.2
3) Функция является четной, так как при перемене знака у любого значения аргумента значение этой функции не изменяется, . Поэтому здесь при составлении таблицы достаточно вычислить значения функции только для положительных значений аргумента; значения функции для отрицательных значений аргумента будут те же.
Составив таблицу, замечаем, что значения аргумента есть числа 1-го порядка, тогда как значения функции — числа 3-го порядка. Поэтому для построения соответствующих точек берем разные масштабы абсцисс и ординат; они показаны числовыми пометками на координатных осях (рис.3).
Рис.3
График данной четной функции симметричен относительно оси ординат.
4) Составим таблицу значений функции для значений аргумента , заключенных на отрезке [—6; 5].
Затем строим точки и, соединяя их сплошной линией, получим искомый график (рис.4).
Данная функция не является четной или нечетной. Поэтому ее график не симметричен ни относительно оси , ни относительно начала координат.
Рис.4
5) Абсциссы точек пересечения графика данной функции с осью найдем из данного уравнения, зная, что в этих точках ордината . При , откуда . Далее составляем таблицу значений данной четной функции на отрезке [—4; 4] и строим ее график (рис.5).
Рис.5
Когда приближается к нулю слева или справа, значения функции и ординаты ее графика неограниченно возрастают. При функция не имеет никакого числового значения, ее график состоит из двух отдельных бесконечных ветвей.
График неявно заданной функции онлайн. Построение графиков функций в Excel. Сервисы для построения графиков функций онлайн
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т.
 д.
д. - Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.

- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.Us или в личном кабинете Onlinecharts.ru. Первый вариант могут использовать все, второй — только зарегистрированные.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .
Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.

- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .
- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .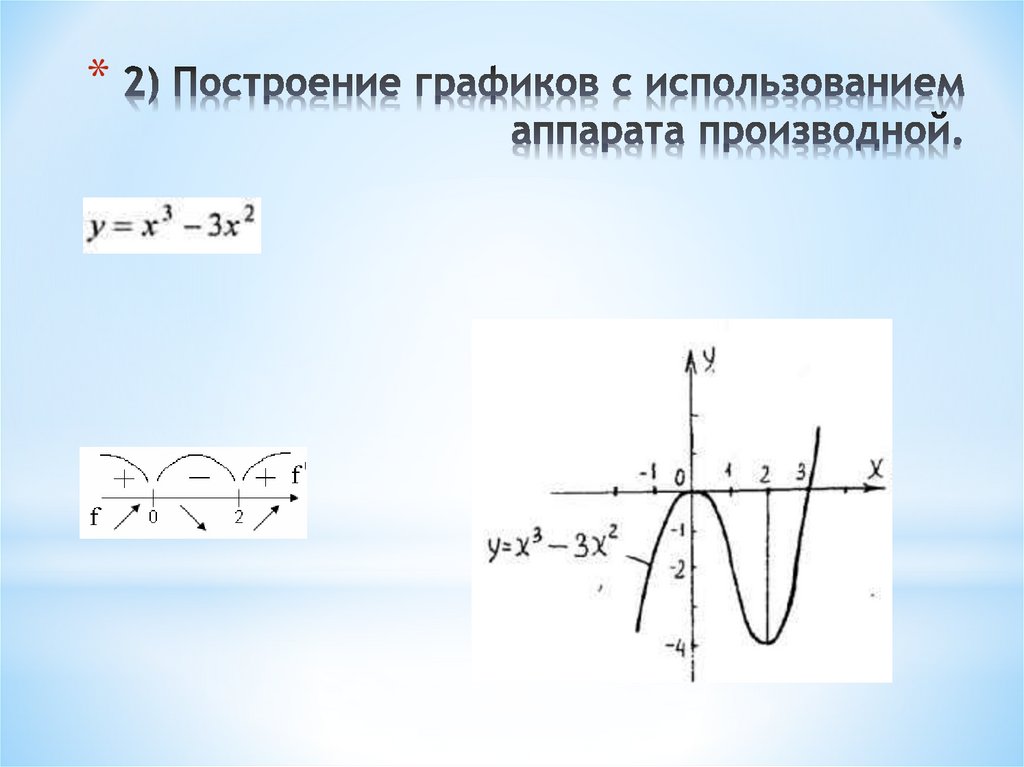
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
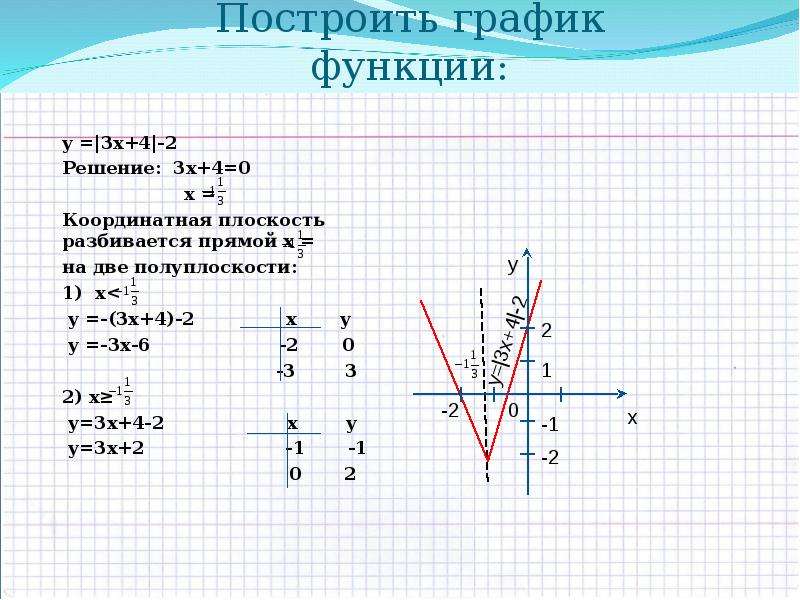
Пример 3 . Построить график функции y = |x 2 — 2x|.
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.
Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.
Также задается и область построения.
Предусмотрена возможность построения графиков онлайн по таблице или без нее. Поддерживается цветовая легенда.
Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.
Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.
Построение графика функции онлайн
ТОП-4 лучших сервиса для построения графиков онлайн
4 бесплатных математических инструмента для создания графиков, которые позволяют создавать их, просто вводя функции, выражения и уравнения. Эти инструменты включает в себя простой и удобный интерфейс, и, как предоставляется, красочный интерфейс, а также возможность вводить нужные функции или выражения. Кроме того, эти инструменты позволяют сохранять созданные графики в различных форматах: PNG, JPG, PDF — и многих другое. GraphGraph представляет собой бесплатное программное обеспечение для создания графиков для Windows, позволяя рисовать графики в системе координат. Можно создать график с использованием часто используемых математических функций, линейных, тригонометрических и т.д. ПО включает регулируемый масштаб, с помощью которого можно легко настроить значение системы координат, как большие, так и малые. Есть возможность применять различные цвета для выделения разных участков графика. Можно рассчитать площадь и длину пути. Инструмент позволяет настроить функции, а также константы. Мало того, он позволяет добавлять текстовые метки, включающие различные шрифты, изображения и объекты. График можно сохранить в различных форматах, таких как JPG, PNG, PDF, SVG, BMP, EMF, GIF. График можно распечатать. Лучшей частью этой бесплатной программы является то, что она позволяет создавать анимацию, с помощью которой можно показать изменения на графике при изменении значения. Скачать Graph FunctyFuncty — другое бесплатное обеспечение для создания математических графиков для Windows, которое позволяет создавать и визуализировать 3D декартовы и сферические математические функции в реальном масштабе времени. Оно позволяет вводить математические функции, мгновенно показывая вид на график и предоставляя вам возможность редактировать нанесенные диапазоны значений, используемых в функциях, X, Y или Z. Есть функция просмотра, где можно вращать, перемещать, масштабировать, а также оценить график. Это бесплатное программное обеспечение поддерживает анимированные функции с временной переменной. Можно сохранить и экспортировать созданный график в PLY-формат, так что он может использоваться в дальнейшем с другими приложениями по 3D моделированию. Скачать Functy Calc5Calc5 является бесплатным онлайн-инструментом для создания математических графиков, который позволяет построить 2D и 3D графики, просто введя нужные математические функции. Попробовать Calc5 Desmos Graphing CalculatorDesmos Graphing Calculator — другой бесплатный онлайн-инструмент, позволяющий создавать простые и сложные графики, просто введя выражения и уравнения вручную или с помощью клавиатуры приложения. Интерфейс яркий и удобный, где можно нарисовать несколько графиков. Бесплатный инструмент позволяет настроить формат бумаги графика, в зависимости от ваших требований. Требуется зарегистрироваться на бесплатном веб-сервисе, чтобы сохранять и делиться созданными графиками с друзьями и коллегами. Попробовать Desmos Graphing Calculator Поделиться:
Оставьте свой комментарий! Добавить комментарий
|
Как построить график функций точек перегиба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.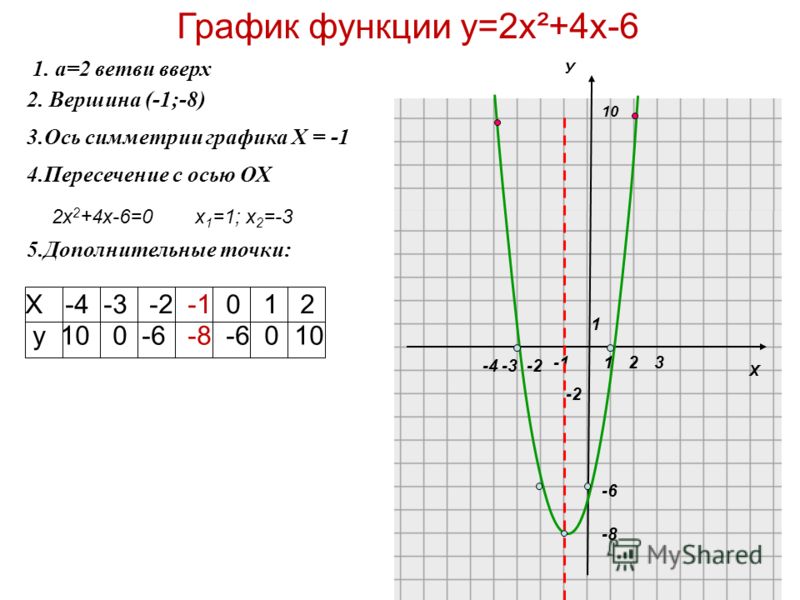 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Калькулятор уклона
По определению, уклон или уклон линии описывает ее крутизну, уклон или уклон. Где м — уклон |
Если известны 2 точки
Если известны 1 точка и наклон
Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается как м . Как правило, крутизна линии измеряется абсолютной величиной ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:
Как правило, крутизна линии измеряется абсолютной величиной ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:
- Линия увеличивается и идет вверх слева направо, когда m> 0
- Линия убывает и идет вниз слева направо, когда m <0
- Линия имеет постоянный наклон и является горизонтальной при m = 0
- Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.
Уклон — это, по сути, изменение высоты при изменении горизонтального расстояния, и его часто называют «подъем через пробег». Он находит применение в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница расстояний между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы учитывать кривизну земли. как фактор.Математически наклон представлен как:
как фактор.Математически наклон представлен как:
В приведенном выше уравнении y 2 — y 1 = Δy или вертикальное изменение, а x 2 — x 1 = Δx или горизонтальное изменение, как показано на представленном графике. Также видно, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x 1 , y 1 ) и (x 2 , y 2 ) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , указанный в калькуляторе выше. Кратко:
d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
Приведенное выше уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:
.Учитывая две точки, можно найти θ , используя следующее уравнение:
m = загар (θ)
По точкам (3,4) и (6,8) найдите наклон прямой, расстояние между двумя точками и угол наклона:
d = √ (6-3) 2 + (8-4) 2 = 5
Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой меняется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.
графиков
графиков Цели
Изучив этот блок, вы сможете:
- Определите оси x и y .
- Определите происхождение . на графике.
- Определите координаты точки x и y .
- Нанесите точки на график.
Элементы графа
Мы часто используем графики, чтобы дать нам представление о
отношения между переменными. Давайте сначала посмотрим на основные
построение графов.
Давайте сначала посмотрим на основные
построение графов.
|
Координаты точек
Точка — это базовая взаимосвязь, отображаемая на графике. Каждая точка
определяется парой чисел, содержащей две координаты. Координата является одним из набора чисел
используется для определения местоположения точки на графике. Каждый
Точка обозначается как x , так и координатой y .
В этом модуле вы узнаете, как найти обе координаты для любого
точка. Вы также узнаете правильные обозначения для обозначения
координаты точки. Сначала вы начнете с определения Координата X точки.
Каждый
Точка обозначается как x , так и координатой y .
В этом модуле вы узнаете, как найти обе координаты для любого
точка. Вы также узнаете правильные обозначения для обозначения
координаты точки. Сначала вы начнете с определения Координата X точки.
Определение координаты x
Координата x балла — это значение, которое сообщает вам, как далеко от начала координат находится точка по горизонтали, или x — ось.Чтобы найти координату x точка на графике:
Справа график с двумя точками, B и D. На этом рисунок:
|
Определение координаты y
Как мы уже упоминали, каждая точка определяется двумя координатами , координаты x и y . Теперь, когда ты знаешь как чтобы найти координату точки x , вы должны уметь чтобы найти координату y .В y — координата точки — это значение, которое говорит вам, как далеко от исходной точки точка находится по вертикали или оси y . Найти y — координата точки на графике:
Оглядываясь на график с нашими точками B и D, мы определите координату y для каждого.
|
Обозначение для опознавания точек
Когда у вас есть координаты точки, вы можете использовать заказанный парное обозначение для маркировки точек.Обозначения просты. Точки идентифицируются указанием их координат в виде ( x , y ). Обратите внимание, что координата x всегда идет первый. Например, на рисунке, который мы использовали, мы определили координаты x и y для каждой точки B и D.
|
Точки на осях
Если точка лежит на оси, рисовать линии не нужно. для определения координат точки.На рисунке ниже
точка A лежит на оси y , а точка C лежит на оси x .
Когда точка лежит на оси, одна из ее координат должна быть равна нулю.
для определения координат точки.На рисунке ниже
точка A лежит на оси y , а точка C лежит на оси x .
Когда точка лежит на оси, одна из ее координат должна быть равна нулю.
|
- Точка C — Если вы посмотрите, как далеко точка
от начала координат по оси y , ответ равен нулю.
Следовательно, координата y равна нулю. Любая точка, которая лежит
на оси x имеет нулевую координату y .

Если вы двигаетесь по оси x , чтобы найти координату x , точка находится в 200 от начала координат. Координаты точки C являются (200, 0)
Пример
|
Ответы на пример
- Какая точка находится на оси y ? Пункт А
- Какая точка помечена (20, 60)? Пункт B
- Какие точки имеют координату y из 30? Пункты A и C
[решение для примера]
Нанесение точек на график
Бывают случаи, когда вам ставят точку, и вам нужно будет найти
его расположение на графике.Этот процесс часто называют
построение точки и использует те же навыки, что и определение координат
точки на графике.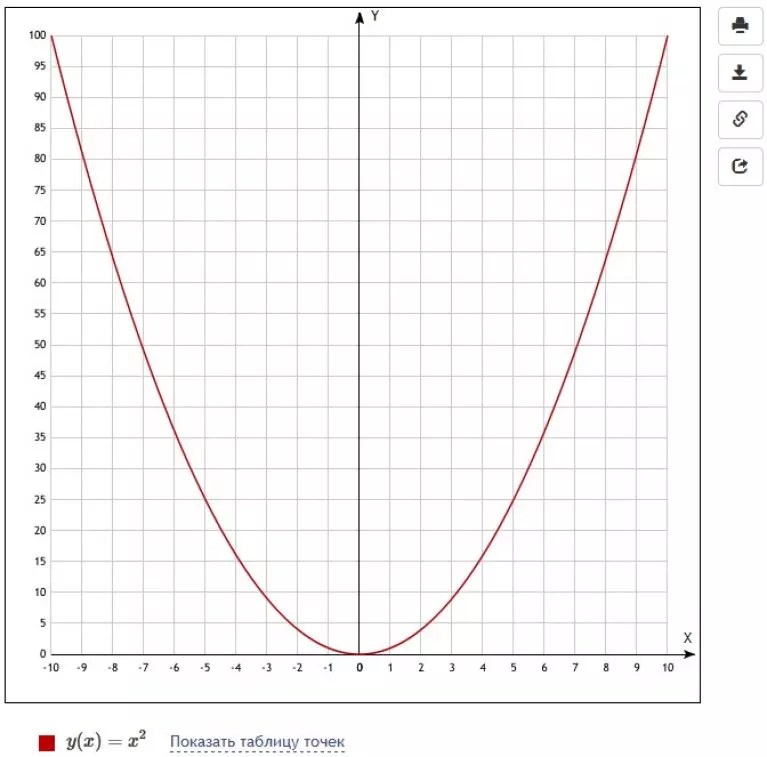 Показан процесс построения точки.
на примере.
Показан процесс построения точки.
на примере.
Пример
Постройте точку (200, 300).
| Шаг первый | Шаг второй | Шаг третий |
|---|---|---|
| Сначала нарисуйте линию, идущую от оси x на x — координата точки.В нашем примере это по адресу 200. | Затем нарисуйте линию, идущую от оси y в точке y — координата точки. В нашем примере это по адресу 300. | Точка пересечения этих двух линий находится в точке, где мы строят, (200, 300). |
Теперь вы готовы попробовать практическую задачу.Если у вас уже есть
выполнил первую практическую задачу для этого блока, который вы можете пожелать
попробовать дополнительную практику.
Эти инструменты, перечисленные ниже, разработаны таким образом, что их можно использовать как автономные приложения в анализ или систематизация чисел и данных. Они являются частью виды деятельности. Алгебра (…) Создайте свой собственный многоугольник и преобразуйте его в декартовой системе координат.Поэкспериментируйте с отражениями через любую линию, вращением вокруг любой линии (что дает трехмерное изображение), вращением вокруг любой точки и перемещением в любом направлении. Связанные темы: углов, исчисление, координата, координатная плоскость, система координат, перевороты, геометрия, скольжения, график, многоугольник, многогранники, отражения, вращение, симметрия, преобразование, перенос, транспонирование Создайте свой собственный аффинный шифр для кодирования и декодирования сообщений. Связанные темы: сложение, арифметика, шифр, криптография, деление, модульное, умножение, шаблон, остатки Управляйте различными типами уравнений конического сечения на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Выберите вертикальную или горизонтальную параболу, круг, эллипс и вертикальную или горизонтальную гиперболу. Связанные темы: алгебра, декартова координата, окружности, коническое сечение, координатная плоскость, эллипс, свойства функции, функции, график, гипербола, парабола, предварительное вычисление, радиус, слайды, перенос Исследуйте поперечные сечения различных геометрических тел: конуса, двойного конуса, цилиндра, пирамиды и призмы. Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление. Связанные темы: алгебра, исчисление, декартова координата, круги, коническое сечение, система координат, эллипс, флаер, график, гипербола, парабола, многоугольник, многогранники, предварительное исчисление, призмы, пирамида, радиус, вращение, преобразование Введите набор точек данных, а затем создайте функцию, соответствующую этим точкам. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, экспонента, показатели степени, свойства функций, функции, график, группировка, целые числа, интервалы, обратные, линейные уравнения, линейные функции, логарифм, умножение, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Просмотр графика и уравнения касательной к любой функции в любой точке функции. Связанные темы: исчисление , декартова координата, координатная плоскость, производная, дифференцирование, свойства функции, график, линейные уравнения, слайды, наклон, касательная Более продвинутая версия Slope Slider, это действие позволяет манипулировать константами и коэффициентами в любой функции, тем самым побуждая пользователя исследовать влияние на график функции путем изменения этих чисел. Связанные темы: алгебра, кривая колокола, исчисление, декартовые координаты, координатная плоскость, система координат, косинус, десятичные дроби, экспонента, флаер, свойства функции, функции, график, интервалы, обратные, линейные уравнения, линейные функции, линии, логарифм , парабола, полином, предварительное вычисление, диапазон, синус, наклон, тангенс, перенос, тригонометрия Студенты могут создавать графики функций, введенных в виде алгебраических выражений, аналогично графическому калькулятору. Связанные темы: алгебра, исчисление, декартова координата, координатная плоскость, косеканс, косинус, котангенс, функции, график, обратные, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Создание графиков функций и наборов упорядоченных пар на одной координатной плоскости. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, экспонента, показатели степени, свойства функций, функции, график, теория графиков, интервалы, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное вычисление, диапазон, секанс, синус, наклон, тангенс, тригонометрия InteGreat! позволяет пользователю визуально изучить идею интеграции путем аппроксимации интегрального значения с помощью разбиений.Пользователь контролирует количество разделов, верхний и нижний пределы, а также метод, используемый для оценки интеграла. Связанные темы: область , исчисление, оценка, свойства функций, функции, график, бесконечность, интеграл, интегрирование, интервалы, предел Студенты создают линейные неравенства и системы линейных неравенств на координатной плоскости. Связанные темы: алгебра, декартова координата, координатная плоскость, график данных, свойства функции, функции, график, неравенство, интервалы, линейные уравнения, линейные функции Введите набор точек данных и функцию или несколько функций, а затем манипулируйте этими функциями, чтобы они соответствовали этим точкам.Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, флаер, свойства функций, функции, график, линейные функции, логарифм, парабола , полином, предварительное вычисление, секущая, синус, слайды, наклон, квадраты, касательная, тригонометрия Учащиеся сравнивают несколько независимых переменных в качестве предикторов одной зависимой переменной. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, график данных, отклонения, флаер, функции, график, линейные функции, квадраты Нанесите упорядоченные пары на график, и они будут связаны в том порядке, в котором они вводятся. Это позволяет вам решить, как пары должны быть соединены, вместо того, чтобы компьютер соединял их слева направо. Связанные темы: декартова координата, координата, координатная плоскость, система координат, график данных, график, линии, проверка вертикальной линии Это упражнение позволяет пользователю исследовать полярную систему координат. Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать представление функции в полярной системе координат. Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Графические рекурсивные функции путем определения f (0) = C и определения f (n) на основе f (n-1). Связанные темы: алгебра, арифметические последовательности, декартовые координаты, координатная плоскость, функции, геометрические последовательности, график, итерация, рекурсия, рекурсивные функции, последовательности Постройте двумерный набор данных, определите линию наилучшего соответствия для их данных, а затем проверьте точность вашей линии наилучшего соответствия. Связанные темы: исчисление , декартова координата, координатная плоскость, корреляция, аппроксимация кривой, график данных, отклонения, остаток, статистика Наносит на график упорядоченные пары и настраивает заголовок графика и метки осей.Точки соединяются слева направо, а не в порядке их ввода. Связанные темы: декартова координата, координата, координатная плоскость, график данных, график, статистика Узнайте о шаблонах чисел в последовательностях и рекурсиях, указав начальное число, множитель и надстройку. Связанные темы: сложение, арифметика, арифметические последовательности, декартовые координаты, координатная плоскость, десятичные числа, геометрические последовательности, график, итерация, умножение, предварительное вычисление, рекурсия, рекурсивные функции, последовательности Постройте упорядоченные пары чисел в виде точечной диаграммы или с соединенными точками.Точки соединяются справа налево, а не в том порядке, в котором они вводятся. Связанные темы: декартова координата, координатная плоскость, система координат, график данных, десятичные дроби, график Подобно другим «флаерам», Slope Slider использует ползунки для изучения влияния множителя и константы на линейную функцию вида f (x) = mx + b. Изучите взаимосвязь между наклоном и пересечением в декартовой системе координат. Связанные темы: алгебра, декартова координата, координатная плоскость, десятичные дроби, флаер, дроби, свойства функции, функции, график, точка пересечения, линейные уравнения, линейные функции, слайды, наклон Введите два комплексных числа (z и c) как упорядоченные пары действительных чисел, затем нажмите кнопку для пошагового итерации. Связанные темы: Комплексное число , координатная плоскость, система координат, экспоненты, фракталы, функции, график, бесконечность, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Исчисление (…) Создайте свой собственный многоугольник и преобразуйте его в декартовой системе координат. Поэкспериментируйте с отражениями через любую линию, вращением вокруг любой линии (что дает трехмерное изображение), вращением вокруг любой точки и перемещением в любом направлении. Связанные темы: углов, исчисление, координата, координатная плоскость, система координат, перевороты, геометрия, скольжения, график, многоугольник, многогранники, отражения, вращение, симметрия, преобразование, перенос, транспонирование Исследуйте поперечные сечения различных геометрических тел: конуса, двойного конуса, цилиндра, пирамиды и призмы. Связанные темы: алгебра, исчисление, декартова координата, круги, коническое сечение, система координат, эллипс, флаер, график, гипербола, парабола, многоугольник, многогранники, предварительное исчисление, призмы, пирамида, радиус, вращение, преобразование Просмотр графика и уравнения касательной к любой функции в любой точке функции. Связанные темы: исчисление , декартова координата, координатная плоскость, производная, дифференцирование, свойства функции, график, линейные уравнения, слайды, наклон, касательная Более продвинутая версия Slope Slider, это действие позволяет манипулировать константами и коэффициентами в любой функции, тем самым побуждая пользователя исследовать влияние на график функции путем изменения этих чисел. Связанные темы: алгебра, кривая колокола, исчисление, декартовые координаты, координатная плоскость, система координат, косинус, десятичные дроби, экспонента, флаер, свойства функции, функции, график, интервалы, обратные, линейные уравнения, линейные функции, линии, логарифм , парабола, полином, предварительное вычисление, диапазон, синус, наклон, тангенс, перенос, тригонометрия Это упражнение позволяет пользователю найти объем и площадь поверхности различных функций, когда они вращаются вокруг осей. Связанные темы: исчисление , декартова координата, координатная плоскость, система координат, косинус, функции, график, синус Студенты могут создавать графики функций, введенных в виде алгебраических выражений, аналогично графическому калькулятору. Связанные темы: алгебра, исчисление, декартова координата, координатная плоскость, косеканс, косинус, котангенс, функции, график, обратные, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Создание графиков функций и наборов упорядоченных пар на одной координатной плоскости.Это похоже на графический калькулятор с расширенными возможностями просмотра. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, экспонента, показатели степени, свойства функций, функции, график, теория графиков, интервалы, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное вычисление, диапазон, секанс, синус, наклон, тангенс, тригонометрия InteGreat! позволяет пользователю визуально изучить идею интеграции путем аппроксимации интегрального значения с помощью разбиений. Связанные темы: область , исчисление, оценка, свойства функций, функции, график, бесконечность, интеграл, интегрирование, интервалы, предел Введите набор точек данных и функцию или несколько функций, а затем манипулируйте этими функциями, чтобы они соответствовали этим точкам. Управляйте функцией на координатной плоскости с помощью ползунков.Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, флаер, свойства функций, функции, график, линейные функции, логарифм, парабола , полином, предварительное вычисление, секущая, синус, слайды, наклон, квадраты, касательная, тригонометрия Это действие позволяет пользователю строить упорядоченные пары и параметрические уравнения на одной и той же координатной плоскости. Связанные темы: исчисление , координатная плоскость, система координат, функции, график, параметрические уравнения, предварительное вычисление Это упражнение позволяет пользователю исследовать полярную систему координат. Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать представление функции в полярной системе координат. Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Постройте двумерный набор данных, определите линию наилучшего соответствия для их данных, а затем проверьте точность вашей линии наилучшего соответствия. Связанные темы: исчисление , декартова координата, координатная плоскость, корреляция, аппроксимация кривой, график данных, отклонения, остаток, статистика Дискретный (. Создайте игровой счетчик с секторами переменного размера, чтобы посмотреть на экспериментальные и теоретические вероятности. Параметры: размеры секторов, количество секторов, количество попыток. Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, проценты, круговая диаграмма, вероятностное моделирование, симуляция, счетчик, статистика, теоретическая вероятность Создайте свой собственный аффинный шифр для кодирования и декодирования сообщений.Введите свою константу и множитель, затем введите сообщение для кодирования. Связанные темы: сложение, арифметика, шифр, криптография, деление, модульное, умножение, шаблон, остатки Работа с различными типами часов для изучения модульных арифметических операций. Параметры: Количество часов на часах. Связанные темы: сложение, деление, прошедшее время, модульное, умножение, остатки, время Вероятностный эксперимент с использованием вертушки фиксированного размера, вертушки переменного сечения, двух
обычные 6-гранные или индивидуальные игральные кости. Связанные темы: кругов, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, результаты, проценты, моделирование вероятности, случайное число, моделирование, счетчик, статистика, теоретическая вероятность, теоретическое значение, испытания Создает сложные геометрические фракталы, задав начальный многоугольник и масштабный коэффициент. Связанные темы: фракталы, геометрия, логарифм, многоугольник, рекурсия, масштаб, самоподобие Введите комплексное значение для «c» в виде упорядоченной пары действительных чисел.Апплет рисует фрактальный набор Джулии для этого начального значения. Связанные темы: Комплексное число , координатная плоскость, система координат, фракталы, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Визуально исследуйте счет и расстановку значений с помощью различных оснований счисления, от 2 до 16 и вплоть до сотен, используя интерфейс, похожий на часы. Связанные темы: арифметика, счет, экспоненты, модульная Графические рекурсивные функции путем определения f (0) = C и определения f (n) на основе f (n-1). Связанные темы: алгебра, арифметические последовательности, декартовые координаты, координатная плоскость, функции, геометрические последовательности, график, итерация, рекурсия, рекурсивные функции, последовательности Узнайте о шаблонах чисел в последовательностях и рекурсиях, указав начальное число, множитель и надстройку.Числа в последовательности отображаются на графике, а также перечислены под графиком. Связанные темы: сложение, арифметика, арифметические последовательности, декартовые координаты, координатная плоскость, десятичные числа, геометрические последовательности, график, итерация, умножение, предварительное вычисление, рекурсия, рекурсивные функции, последовательности Создайте игровой счетчик с одним-двенадцатью секторами, чтобы посмотреть на экспериментальные и теоретические вероятности. Связанные темы: углов, круговой график, круги, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, круговая диаграмма, вероятность, моделирование вероятности, счетчик, теоретическая вероятность, теоретическое значение, испытания Исследуйте фракталы, исследуя отношения между множеством Мандельброта и множествами Жюлиа. Связанные темы: хаос, комплексное число, координата, координатная плоскость, экспоненты, фракталы, функции, геометрические последовательности, геометрия, итерация, множество Джулии, множество Мандельброта, шаблон, рекурсия, рекурсивные функции, самоподобие, наборы Геометрия (…) Создайте свой собственный многоугольник и преобразуйте его в декартовой системе координат. Поэкспериментируйте с отражениями через любую линию, вращением вокруг любой линии (что дает трехмерное изображение), вращением вокруг любой точки и перемещением в любом направлении. Связанные темы: углов, исчисление, координата, координатная плоскость, система координат, перевороты, геометрия, скольжения, график, многоугольник, многогранники, отражения, вращение, симметрия, преобразование, перенос, транспонирование Попрактикуйтесь в чтении часов, введите время для отображения на часах или позвольте часам генерировать случайное время для чтения.Выбирайте из трех уровней сложности. Clock Wise — один из исследователей интерактивного оценивания. Связанные темы: оценка , прошедшее время, время Управляйте различными типами уравнений конического сечения на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Выберите вертикальную или горизонтальную параболу, круг, эллипс и вертикальную или горизонтальную гиперболу. Связанные темы: алгебра, декартова координата, окружности, коническое сечение, координатная плоскость, эллипс, свойства функции, функции, график, гипербола, парабола, предварительное вычисление, радиус, слайды, перенос Исследуйте поперечные сечения различных геометрических тел: конуса, двойного конуса, цилиндра, пирамиды и призмы. Связанные темы: алгебра, исчисление, декартова координата, круги, коническое сечение, система координат, эллипс, флаер, график, гипербола, парабола, многоугольник, многогранники, предварительное исчисление, призмы, пирамида, радиус, вращение, преобразование Создайте свои собственные фракталы, нарисовав «правило деформации линии» и пошагово создавая геометрический фрактал.Параметры: Тип сетки, количество точек изгиба на линии. Связанные темы: хаос, фракталы, геометрические последовательности, итерация, узор, предварительное вычисление, рекурсия, масштаб, самоподобие, последовательности, симметрия, преобразование Создайте «плитку пола», перетаскивая углы четырехугольника. Узнайте о мозаике четырехугольных фигур, когда построенная вами фигура накладывается на область. Связанные темы: углов, площадь, координатная плоскость, система координат, длина, узор, плоскости, четырехугольники, прямоугольники, отражения, ромб, вращение, слайды, симметрия, мозаика, преобразование, перенос Создает сложные геометрические фракталы, задав начальный многоугольник и масштабный коэффициент. Связанные темы: фракталы, геометрия, логарифм, многоугольник, рекурсия, масштаб, самоподобие Измерение углов, расстояний и площадей на нескольких различных изображениях (выбор включает карты, аэрофотоснимки и другие). Функция масштабирования позволяет пользователю установить масштаб, используемый для измерения расстояний и площадей. Связанные темы: алгебра, углы, площадь, размер, интервалы, длина, пропорция, масштаб, преобразование Введите комплексное значение для «c» в виде упорядоченной пары действительных чисел.Апплет рисует фрактальный набор Джулии для этого начального значения. Связанные темы: Комплексное число , координатная плоскость, система координат, фракталы, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Нанесите упорядоченные пары на график, и они будут связаны в том порядке, в котором они вводятся. Это позволяет вам решить, как пары должны быть соединены, вместо того, чтобы компьютер соединял их слева направо. Связанные темы: декартова координата, координата, координатная плоскость, система координат, график данных, график, линии, проверка вертикальной линии Постройте упорядоченные пары чисел в виде точечной диаграммы или с соединенными точками. Точки соединяются справа налево, а не в том порядке, в котором они вводятся. Связанные темы: декартова координата, координатная плоскость, система координат, график данных, десятичные дроби, график Работает как настоящий секундомер, записывая время по вашему выбору.Этот секундомер показывает точность до десятых долей секунды. Параметры: отсчет от 0 или обратный отсчет от установленного времени. Связанные темы: десятичных знаков, прошедшее время, интервалы, секундомер, время Управляйте размерами многогранников и наблюдайте за изменением площади поверхности и объема. Параметры: Тип многогранника, длина, ширина и высота. Площадь поверхности и объем один из исследователей интерактивной оценки. Связанные темы: оценка , размер, геометрия, длина, многогранники, призмы, площадь поверхности, объем Создайте мозаику, деформируя треугольник, прямоугольник или шестиугольник, чтобы сформировать многоугольник, перекрывающий плоскость.Углы полигонов можно перетаскивать, а соответствующие края полигонов можно перетаскивать. Параметры: Цвета, начальный многоугольник. Связанные темы: углов, площадь, переворот, геометрия, скольжения, шестиугольник, длина, узор, плоскости, многоугольник, отражения, вращение, слайды, квадраты, симметрия, мозаика Исследуйте фракталы, исследуя отношения между множеством Мандельброта и множествами Жюлиа. Связанные темы: хаос, комплексное число, координата, координатная плоскость, экспоненты, фракталы, функции, геометрические последовательности, геометрия, итерация, множество Джулии, множество Мандельброта, шаблон, рекурсия, рекурсивные функции, самоподобие, наборы Исследуйте мир перемещений, отражений и вращений в декартовой системе координат, преобразовывая квадраты, треугольники и параллелограммы. Связанные темы: декартова координата, координатная плоскость, система координат, перевороты, геометрия, скольжения, график, шестиугольник, изображение, многоугольник, предварительное изображение, отражения, вращение, симметрия, преобразование, перенос, транспонирование, треугольник, треугольники Создайте свой собственный многоугольник и преобразуйте его в декартовой системе координат. Поэкспериментируйте с отражениями поперек любой линии, вращением вокруг любой точки и перемещением в любом направлении.Параметры: форма, перемещение по оси x или y, отражение по оси x или y, угол поворота Связанные темы: углов, декартова координата, координата, координатная плоскость, система координат, переворот, геометрия, скольжение, график, изображение, линейные уравнения, многоугольник, предварительное изображение, отражения, вращение, симметрия, преобразование, перенос, транспонирование Введите два комплексных числа (z и c) как упорядоченные пары действительных чисел, затем нажмите кнопку для пошагового итерации. Связанные темы: Комплексное число , координатная плоскость, система координат, экспоненты, фракталы, функции, график, бесконечность, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Графики (…) Создайте свой собственный многоугольник и преобразуйте его в декартовой системе координат.Поэкспериментируйте с отражениями через любую линию, вращением вокруг любой линии (что дает трехмерное изображение), вращением вокруг любой точки и перемещением в любом направлении. Связанные темы: углов, исчисление, координата, координатная плоскость, система координат, перевороты, геометрия, скольжения, график, многоугольник, многогранники, отражения, вращение, симметрия, преобразование, перенос, транспонирование Введите данные для создания гистограммы, а затем измените многие параметры внешнего вида диаграммы. Связанные темы: гистограмма , график данных, гистограмма, статистика Учащиеся могут создавать коробчатые диаграммы для встроенных или заданных пользователем данных, а также экспериментировать с выбросами. Пользователь может выбрать, использовать или не использовать медианное значение для расчета межквартильного размаха. Связанные темы: прямоугольник и усы , прямоугольная диаграмма, координатная плоскость, график данных, медиана, выбросы, проценты, квартиль, диапазон, масштаб, асимметричное распределение, статистика Исследуйте поперечные сечения различных геометрических тел: конуса, двойного конуса, цилиндра, пирамиды и призмы.Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление. Связанные темы: алгебра, исчисление, декартова координата, круги, коническое сечение, система координат, эллипс, флаер, график, гипербола, парабола, многоугольник, многогранники, предварительное исчисление, призмы, пирамида, радиус, вращение, преобразование InteGreat! позволяет пользователю визуально изучить идею интеграции путем аппроксимации интегрального значения с помощью разбиений. Связанные темы: область , исчисление, оценка, свойства функций, функции, график, бесконечность, интеграл, интегрирование, интервалы, предел Введите данные для создания двойной гистограммы, а затем измените максимальные и минимальные значения графика. Связанные темы: гистограмма , график данных, двойная гистограмма Создайте круговую диаграмму, регулируя размер делений с помощью мыши или вводя значения.Параметры: количество разделов, размер разделов, использовать проценты или дроби. Связанные темы: углов, площадь, круговая диаграмма, круги, дроби, проценты, проценты, круговая диаграмма, пропорции, статистика Это упражнение позволяет пользователю исследовать полярную систему координат. Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать представление функции в полярной системе координат. Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Графические рекурсивные функции путем определения f (0) = C и определения f (n) на основе f (n-1). Связанные темы: алгебра, арифметические последовательности, декартовые координаты, координатная плоскость, функции, геометрические последовательности, график, итерация, рекурсия, рекурсивные функции, последовательности Постройте двумерный набор данных, определите линию наилучшего соответствия для их данных, а затем проверьте точность вашей линии наилучшего соответствия. Связанные темы: исчисление , декартова координата, координатная плоскость, корреляция, аппроксимация кривой, график данных, отклонения, остаток, статистика Наносит на график упорядоченные пары и настраивает заголовок графика и метки осей. Связанные темы: декартова координата, координата, координатная плоскость, график данных, график, статистика Моделирование (…) Введите набор точек данных, а затем создайте функцию, соответствующую этим точкам. Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, экспонента, показатели степени, свойства функций, функции, график, группировка, целые числа, интервалы, обратные, линейные уравнения, линейные функции, логарифм, умножение, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Введите набор точек данных и функцию или несколько функций, а затем манипулируйте этими функциями, чтобы они соответствовали этим точкам. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, флаер, свойства функций, функции, график, линейные функции, логарифм, парабола , полином, предварительное вычисление, секущая, синус, слайды, наклон, квадраты, касательная, тригонометрия Учащиеся сравнивают несколько независимых переменных в качестве предикторов одной зависимой переменной.Студенты изучают корреляцию и линии наилучшего соответствия. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, график данных, отклонения, флаер, функции, график, линейные функции, квадраты Номер и операции (…) Создайте свой собственный аффинный шифр для кодирования и декодирования сообщений. Связанные темы: сложение, арифметика, шифр, криптография, деление, модульное, умножение, шаблон, остатки Работа с различными типами часов для изучения модульных арифметических операций.Параметры: Количество часов на часах. Связанные темы: сложение, деление, прошедшее время, модульное, умножение, остатки, время Преобразует дроби в десятичные и десятичные в дроби. Наблюдайте за отношениями между дроби и десятичные дроби. Связанные темы: десятичные дроби, деление, дроби, рациональные числа Создайте свои собственные фракталы, нарисовав «правило деформации линии» и пошагово создавая геометрический фрактал.Параметры: Тип сетки, количество точек изгиба на линии. Связанные темы: хаос, фракталы, геометрические последовательности, итерация, узор, предварительное вычисление, рекурсия, масштаб, самоподобие, последовательности, симметрия, преобразование Введите комплексное значение для «c» в виде упорядоченной пары действительных чисел. Связанные темы: Комплексное число , координатная плоскость, система координат, фракталы, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Смеси позволяет исследовать проценты через две стопки цветных и неокрашенных фишек.Пользователь должен решить, сколько фишек окрасить, чтобы получить желаемый процент цветных фишек по сравнению с общей стопкой. Mixtures — один из исследователей интерактивного оценивания. Связанные темы: оценка, подсчет, проценты, проценты, пропорции, наборы Визуально исследуйте счет и расстановку значений с помощью различных оснований счисления, от 2 до 16 и вплоть до сотен, используя интерфейс, похожий на часы.Это упражнение также позволяет вам смотреть на числа на часах в базе 10 или в другой выбранной вами базе, чтобы изучить взаимосвязь между этими значениями. Связанные темы: арифметика, счет, экспоненты, модульная Графические рекурсивные функции путем определения f (0) = C и определения f (n) на основе f (n-1). Связанные темы: алгебра, арифметические последовательности, декартовые координаты, координатная плоскость, функции, геометрические последовательности, график, итерация, рекурсия, рекурсивные функции, последовательности Узнайте о шаблонах чисел в последовательностях и рекурсиях, указав начальное число, множитель и надстройку.Числа в последовательности отображаются на графике, а также перечислены под графиком. Связанные темы: сложение, арифметика, арифметические последовательности, декартовые координаты, координатная плоскость, десятичные числа, геометрические последовательности, график, итерация, умножение, предварительное вычисление, рекурсия, рекурсивные функции, последовательности Исследуйте фракталы, исследуя отношения между множеством Мандельброта и множествами Жюлиа. Связанные темы: хаос, комплексное число, координата, координатная плоскость, экспоненты, фракталы, функции, геометрические последовательности, геометрия, итерация, множество Джулии, множество Мандельброта, шаблон, рекурсия, рекурсивные функции, самоподобие, наборы Введите два комплексных числа (z и c) как упорядоченные пары действительных чисел, затем нажмите кнопку для пошагового итерации. Связанные темы: Комплексное число , координатная плоскость, система координат, экспоненты, фракталы, функции, график, бесконечность, итерация, множество Джулии, множество Мандельброта, рекурсия, рекурсивные функции, наборы Вероятность (…) Создайте игровой счетчик с секторами переменного размера, чтобы посмотреть на экспериментальные и теоретические вероятности.Параметры: размеры секторов, количество секторов, количество попыток. Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, проценты, круговая диаграмма, вероятностное моделирование, симуляция, счетчик, статистика, теоретическая вероятность Вероятностный эксперимент с использованием вертушки фиксированного размера, вертушки переменного сечения, двух
обычные 6-гранные или индивидуальные игральные кости. Связанные темы: кругов, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, результаты, проценты, моделирование вероятности, случайное число, моделирование, счетчик, статистика, теоретическая вероятность, теоретическое значение, испытания В этом апплете вы можете настроить параметры двух кривых Гаусса, чтобы определить, есть ли возможность различия между двумя средними. Связанные темы: кривая колокола, непрерывное распределение, экспериментальная вероятность, экспонента, график, интеграл, среднее значение, нормальное распределение, стандартное отклонение, статистика, теоретическая вероятность Создайте игровой счетчик с одним-двенадцатью секторами, чтобы посмотреть на экспериментальные и теоретические вероятности.Параметры: количество секторов, количество попыток. Связанные темы: углов, круговой график, круги, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, круговая диаграмма, вероятность, моделирование вероятности, счетчик, теоретическая вероятность, теоретическое значение, испытания Статистика (. Создайте игровой счетчик с секторами переменного размера, чтобы посмотреть на экспериментальные и теоретические вероятности.Параметры: размеры секторов, количество секторов, количество попыток. Связанные темы: углов, круговой график, круги, подсчет, десятичные дроби, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, проценты, круговая диаграмма, вероятностное моделирование, симуляция, счетчик, статистика, теоретическая вероятность Введите данные для создания гистограммы, а затем измените многие параметры внешнего вида диаграммы. Связанные темы: гистограмма , график данных, гистограмма, статистика Учащиеся могут создавать коробчатые диаграммы для встроенных или заданных пользователем данных, а также экспериментировать с выбросами.Пользователь может выбрать, использовать или не использовать медианное значение для расчета межквартильного размаха. Связанные темы: прямоугольник и усы , прямоугольная диаграмма, координатная плоскость, график данных, медиана, выбросы, проценты, квартиль, диапазон, масштаб, асимметричное распределение, статистика Введите свои собственные категории данных и значение каждой категории, чтобы создать круговую диаграмму. Есть также встроены наборы данных, которые можно просматривать. Связанные темы: углов, площадь, круговая диаграмма, круги, график данных, дроби, проценты, круговая диаграмма, пропорция, статистика Введите набор точек данных, а затем создайте функцию, соответствующую этим точкам.Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, экспонента, показатели степени, свойства функций, функции, график, группировка, целые числа, интервалы, обратные, линейные уравнения, линейные функции, логарифм, умножение, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Вероятностный эксперимент с использованием вертушки фиксированного размера, вертушки переменного сечения, двух
обычные 6-гранные или индивидуальные игральные кости. Связанные темы: кругов, события, экспериментальная вероятность, справедливая, дроби, геометрическая вероятность, результаты, проценты, моделирование вероятности, случайное число, моделирование, счетчик, статистика, теоретическая вероятность, теоретическое значение, испытания Этот апплет позволяет пользователю экспериментировать со случайно сгенерированными наборами данных при различных размерах выборки и стандартных отклонениях. Затем пользователи могут сравнить распределение экспериментальных данных с ожидаемым распределением. Связанные темы: кривая колокола , непрерывное распределение, экспонента, гистограмма, бесконечность, среднее значение, меры центральной тенденции, нормальное распределение, вероятностное моделирование, статистика, испытания Создание графиков функций и наборов упорядоченных пар на одной координатной плоскости. Это похоже на графический калькулятор с расширенными возможностями просмотра. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, экспонента, показатели степени, свойства функций, функции, график, теория графиков, интервалы, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное вычисление, диапазон, секанс, синус, наклон, тангенс, тригонометрия Просмотр гистограмм для встроенных или заданных пользователем данных.Поэкспериментируйте, как размер интервалов классов влияет на внешний вид гистограммы. Параметры: наборы данных, размеры классов. Связанные темы: подсчет, график данных, график, гистограмма, интервалы, среднее значение, диапазон, асимметричное распределение, слайды, стандартное отклонение Введите данные и просмотрите среднее, медианное значение, дисперсию и стандартное отклонение набора данных. Связанные темы: десятичных знаков, отклонения, среднее значение, меры центральной тенденции, медиана, режим, диапазон, моделирование, стандартное отклонение, статистика, дисперсия Введите данные для создания двойной гистограммы, а затем измените максимальные и минимальные значения графика. Связанные темы: гистограмма , график данных, двойная гистограмма Введите набор точек данных и функцию или несколько функций, а затем манипулируйте этими функциями, чтобы они соответствовали этим точкам.Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, флаер, свойства функций, функции, график, линейные функции, логарифм, парабола , полином, предварительное вычисление, секущая, синус, слайды, наклон, квадраты, касательная, тригонометрия Учащиеся сравнивают несколько независимых переменных в качестве предикторов одной зависимой переменной. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, график данных, отклонения, флаер, функции, график, линейные функции, квадраты Измените стандартное отклонение автоматически созданного нормального распределения, чтобы создать новую гистограмму. Обратите внимание, насколько хорошо гистограмма соответствует кривой и насколько области под кривой соответствуют количеству испытаний.Параметры: стандартное отклонение, количество испытаний, интервалы классов. Связанные темы: кривая колокола , непрерывное распределение, экспонента, гистограмма, бесконечность, среднее значение, меры центральной тенденции, нормальное распределение, моделирование вероятности, стандартное отклонение, статистика, испытания Нанесите упорядоченные пары на график, и они будут связаны в том порядке, в котором они вводятся. Это позволяет вам решить, как пары должны быть соединены, вместо того, чтобы компьютер соединял их слева направо. Связанные темы: декартова координата, координата, координатная плоскость, система координат, график данных, график, линии, проверка вертикальной линии В этом апплете вы можете настроить параметры двух кривых Гаусса, чтобы определить, есть ли возможность различия между двумя средними. Связанные темы: кривая колокола, непрерывное распределение, экспериментальная вероятность, экспонента, график, интеграл, среднее значение, нормальное распределение, стандартное отклонение, статистика, теоретическая вероятность Создайте круговую диаграмму, регулируя размер делений с помощью мыши или вводя значения.Параметры: количество разделов, размер разделов, использовать проценты или дроби. Связанные темы: углов, площадь, круговая диаграмма, круги, дроби, проценты, проценты, круговая диаграмма, пропорции, статистика PlopIt позволяет пользователям строить точечные графики данных с помощью мыши. Связанные темы: гистограмма , график данных, график, гистограмма, среднее значение, меры центральной тенденции, медиана, режим, диапазон, статистика Постройте двумерный набор данных, определите линию наилучшего соответствия для их данных, а затем проверьте точность вашей линии наилучшего соответствия. Связанные темы: исчисление , декартова координата, координатная плоскость, корреляция, аппроксимация кривой, график данных, отклонения, остаток, статистика Наносит на график упорядоченные пары и настраивает заголовок графика и метки осей. Точки соединяются слева направо, а не в порядке их ввода. Связанные темы: декартова координата, координата, координатная плоскость, график данных, график, статистика Постройте упорядоченные пары чисел в виде точечной диаграммы или с соединенными точками. Связанные темы: декартова координата, координатная плоскость, система координат, график данных, десятичные дроби, график Измените медиану и стандартное отклонение автоматически сгенерированного нормального распределения, чтобы создать искаженное распределение, позволяя вам наблюдать такие свойства, как различие между средним, медианным и модой.Параметры: медиана, стандартное отклонение, количество испытаний, интервалы классов. Связанные темы: кривая колокола , непрерывное распределение, гистограмма, среднее значение, меры центральной тенденции, медиана, нормальное распределение, асимметричное распределение, стандартное отклонение, статистика, испытания, дисперсия Создайте игровой счетчик с одним-двенадцатью секторами, чтобы посмотреть на экспериментальные и теоретические вероятности. Параметры: количество секторов, количество попыток. Связанные темы: углов, круговой график, круги, события, экспериментальная вероятность, удовлетворительная, геометрическая вероятность, результаты, проценты, круговая диаграмма, вероятность, моделирование вероятности, счетчик, теоретическая вероятность, теоретическое значение, испытания Просмотрите графики стеблей и листьев своих собственных данных, а затем потренируйтесь находить средние значения, медианы и моды. Stem and Leaf Plotter — один из исследователей интерактивной оценки. Связанные темы: оценка , график данных, график, среднее значение, меры центральной тенденции, медиана, режим, диапазон, статистика, стебель и лист Тригонометрия (…) Введите набор точек данных, а затем создайте функцию, соответствующую этим точкам. Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, экспонента, показатели степени, свойства функций, функции, график, группировка, целые числа, интервалы, обратные, линейные уравнения, линейные функции, логарифм, умножение, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Более продвинутая версия Slope Slider, это действие позволяет манипулировать константами и коэффициентами в любой функции, тем самым побуждая пользователя исследовать влияние на график функции путем изменения этих чисел. Связанные темы: алгебра, кривая колокола, исчисление, декартовые координаты, координатная плоскость, система координат, косинус, десятичные дроби, экспонента, флаер, свойства функции, функции, график, интервалы, обратные, линейные уравнения, линейные функции, линии, логарифм , парабола, полином, предварительное вычисление, диапазон, синус, наклон, тангенс, перенос, тригонометрия Студенты могут создавать графики функций, введенных в виде алгебраических выражений, аналогично графическому калькулятору. Связанные темы: алгебра, исчисление, декартова координата, координатная плоскость, косеканс, косинус, котангенс, функции, график, обратные, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное исчисление, диапазон, секущая, синус, наклон, тангенс, тригонометрия Создание графиков функций и наборов упорядоченных пар на одной координатной плоскости. Это похоже на графический калькулятор с расширенными возможностями просмотра. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, экспонента, показатели степени, свойства функций, функции, график, теория графиков, интервалы, линейные уравнения, линейные функции, логарифм, парабола, полином, положительная часть операнда, предварительное вычисление, диапазон, секанс, синус, наклон, тангенс, тригонометрия Введите набор точек данных и функцию или несколько функций, а затем манипулируйте этими функциями, чтобы они соответствовали этим точкам.Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Связанные темы: алгебра, исчисление, декартова координата, координата, координатная плоскость, система координат, косеканс, косинус, котангенс, аппроксимация кривой, график данных, отклонения, флаер, свойства функций, функции, график, линейные функции, логарифм, парабола , полином, предварительное вычисление, секущая, синус, слайды, наклон, квадраты, касательная, тригонометрия Это упражнение позволяет пользователю исследовать полярную систему координат. Связанные темы: исчисление , координатная плоскость, система координат, косинус, график данных, график, полярные координаты, предварительное вычисление, синус, тангенс, тригонометрия Наука (…) Попрактикуйтесь в чтении часов, введите время для отображения на часах или позвольте часам генерировать случайное время для чтения.Выбирайте из трех уровней сложности. Clock Wise — один из исследователей интерактивного оценивания. Связанные темы: оценка , прошедшее время, время |
Эскиз кривой
В процессе построения кривой выполняются следующие шаги:
\ (1. \) Домен
Найдите область определения функции и определите точки разрыва (если есть).
\ (2. \) Перехватывает
Определите точки пересечения \ (x- \) и \ (y — \) функции, если это возможно.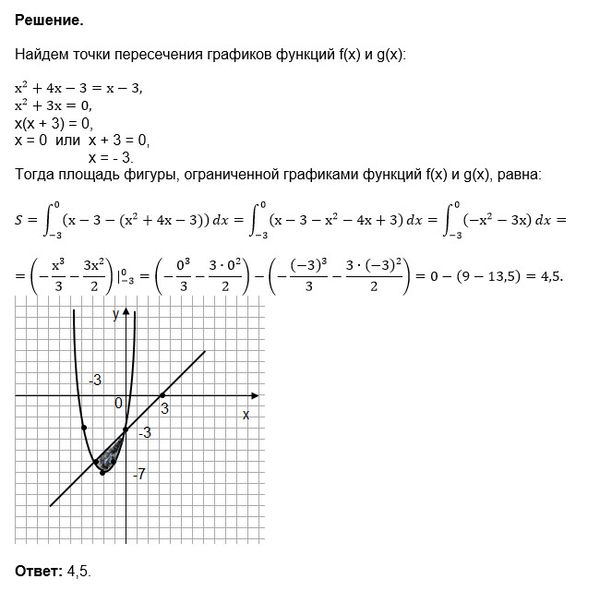 Чтобы найти точку пересечения \ (x — \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x. \). Аналогично, мы устанавливаем \ (x = 0 \), чтобы найти \ (y- \ ) перехват. Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо). \)
Чтобы найти точку пересечения \ (x — \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x. \). Аналогично, мы устанавливаем \ (x = 0 \), чтобы найти \ (y- \ ) перехват. Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо). \)
\ (3. \) Симметрия
Определите, является ли функция четной, нечетной или ни одной, и проверьте периодичность функции.Если \ (f \ left ({- x} \ right) = f \ left (x \ right) \) для всех \ (x \) в области, то \ (f \ left (x \ right) \) является четный и симметричный относительно оси \ (y — \). Если \ (f \ left ({- x} \ right) = -f \ left (x \ right) \) для всех \ (x \) в домене, то \ (f \ left (x \ right) \) нечетное и симметричное относительно начала координат.
\ (4. \) Асимптоты
Найдите вертикальную, горизонтальную и наклонную (наклонную) асимптоты функции.
\ (5. \) Интервалы увеличения и уменьшения
Вычислите первую производную \ (f ^ \ prime \ left (x \ right) \) и найдите критические точки функции. 2}} \ right]}
+ {2 — \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
— {\ frac {{\ sqrt 3}} {9} — \ cancel {3}}
+ {2 \ sqrt 3 — \ cancel {1} + \ cancel {2}}
— {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 — \ sqrt 3 — 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]
2}} \ right]}
+ {2 — \ frac {{2 \ sqrt 3}} {3}}
= {\ cancel {1} - \ sqrt 3 + \ cancel {1}}
— {\ frac {{\ sqrt 3}} {9} — \ cancel {3}}
+ {2 \ sqrt 3 — \ cancel {1} + \ cancel {2}}
— {\ frac {{2 \ sqrt 3}} {3}}
= {\ frac {{9 \ sqrt 3 — \ sqrt 3 — 6 \ sqrt 3}} {9}}
= {\ frac {{2 \ sqrt 3}} {9} \ приблизительно 0,38;}
\]
Аналогично находим, что
\ [
{y \ left ({1 + \ frac {{\ sqrt 3}} {3}} \ right)}
= — {\ frac {{2 \ sqrt 3}} {9} \ приблизительно -0 , 38.}
\]
Таким образом, функция имеет локальный максимум в точке
\ [\ left ({1 — \ frac {{\ sqrt 3}} {3}, \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({0,42; \ ; 0,38} \ вправо). \]
Соответственно, локальный минимум достигается в точке
.\ [\ left ({1 + \ frac {{\ sqrt 3}} {3}, — \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({1,58; \; — 0,38} \ вправо) \]
Интервалы увеличения / уменьшения следуют из рисунка \ (1a. \)
Рассмотрим вторую производную:
\ [
{y ^ {\ prime \ prime} \ left (x \ right) = {\ left ({3 {x ^ 2} — 6x + 2} \ right) ^ \ prime}}
= {6x — 6;}
\]
\ [
{y ^ {\ prime \ prime} \ left (x \ right) = 0, \; \;} \ Rightarrow
{6x — 6 = 0, \; \;} \ Rightarrow
{x = 1 . 2}}
2}}
= {\ left ({x + 2} \ right) \ left ({2x — \ cancel {2} + x + \ cancel {2}} \ right)}
= {3x \ left ({x + 2} \ вправо).}
\]
Стационарных точек
\ [
{y ‘\ left (x \ right) = 0, \; \;} \ Rightarrow
{3x \ left ({x + 2} \ right) = 0, \; \;} \ Rightarrow
{ {x_1} = 0, \; {x_2} = — 2.}
\]
Производная меняет знак, как показано на рисунке \ (3a. \). Следовательно, \ (x = -2 \) — точка максимума, а \ (x = 0 \) — точка минимума. В этих экстремальных точках функция имеет следующие значения:
\ [
{y \ left ({- 2} \ right) = — 4,} \; \; \; \ kern-0.3}}} = 0, \; \;} \ Rightarrow
{{x_1} = — \ sqrt 3, \; {x_2} = \ sqrt 3.}
\]
При прохождении через эти точки вторая производная меняет знак. Следовательно, обе точки являются точками перегиба. Функция строго выпуклая вниз в интервалах \ (\ left ({- \ infty, — \ sqrt 3} \ right) \) и \ (\ left ({\ sqrt 3, + \ infty} \ right) \) и соответственно, строго выпукло вверх в интервале \ (\ left ({- \ sqrt 3, \ sqrt 3} \ right). 2} + 1}} {{\ cancel {1} - \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 — 2 \ sqrt 2 + 2 + 1}} {{- \ sqrt 2}}} = {\ frac {{4 — 2 \ sqrt 2}} {{- \ sqrt 2}}} = {\ frac {{4 — 4 \ sqrt 2}} {2}} = {2 \ left ({1 — \ sqrt 2} \ right) \ приблизительно {- 0.2} + 1}} {{\ cancel {1} + \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 + 2 \ sqrt 2 + 2 + 1}} {{\ sqrt 2} }} = {\ frac {{4 + 2 \ sqrt 2}} {{\ sqrt 2}}} = {\ frac {{4 + 4 \ sqrt 2}} {2}} = {2 \ left ({1 + \ sqrt 2} \ right) \ приблизительно {4.83}} \]
2} + 1}} {{\ cancel {1} - \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 — 2 \ sqrt 2 + 2 + 1}} {{- \ sqrt 2}}} = {\ frac {{4 — 2 \ sqrt 2}} {{- \ sqrt 2}}} = {\ frac {{4 — 4 \ sqrt 2}} {2}} = {2 \ left ({1 — \ sqrt 2} \ right) \ приблизительно {- 0.2} + 1}} {{\ cancel {1} + \ sqrt 2 — \ cancel {1}}}} = {\ frac {{1 + 2 \ sqrt 2 + 2 + 1}} {{\ sqrt 2} }} = {\ frac {{4 + 2 \ sqrt 2}} {{\ sqrt 2}}} = {\ frac {{4 + 4 \ sqrt 2}} {2}} = {2 \ left ({1 + \ sqrt 2} \ right) \ приблизительно {4.83}} \]
Теперь мы можем нарисовать график функции (рисунок \ (5b \)).
Графические производные
Примеры 7.2 — Графический анализ с использованием первой и второй производных Пусть 3 2 1 () x x f x. Найдите каждое из следующего: (a) Домен, точки пересечения по оси x, точки пересечения по оси Y (e) Интервалы увеличения / уменьшения и локальные (b) Вертикальные асимптоты и близкие экстремумы поведения (c) Горизонтальные асимптоты (f) Интервалы вогнутости, и перегиб являются решающими, производная, которую они находят, или определенный интеграл, который они вычисляют.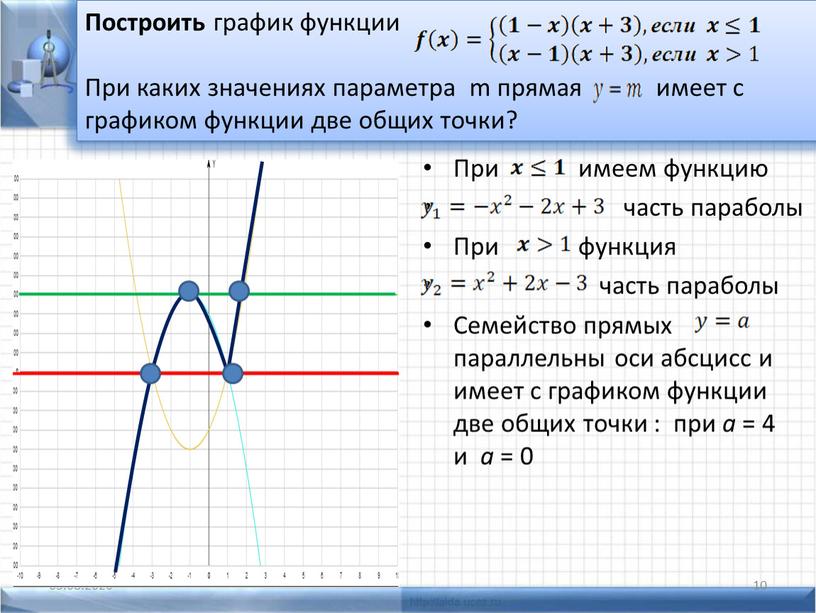 Настройка должна быть записана в стандартных математических обозначениях, а не в обозначениях калькулятора; им не нужно показывать другие работы. 1. Изобразите функцию в соответствующем окне. а.
Настройка должна быть записана в стандартных математических обозначениях, а не в обозначениях калькулятора; им не нужно показывать другие работы. 1. Изобразите функцию в соответствующем окне. а.
Вычисление и графическое отображение производных функций и параметрических уравнений. Медицинская клиника Wvu University Town Center Описание Complete Graphing Calculator — это уникальное приложение, которое содержит многофункциональный графический калькулятор с возможностью построения четырех различных уравнений одновременно, а также с возможностью получения производной и пересечения… Трехкомпонентный граф изменяющей цвет производной, построение графика производной функции, производной от функций синуса и косинуса (быстрое исследование)
Помните, что производная y по x записывается как dy / dx. Вторая производная записывается как d 2 y / dx 2, произносится как «ди два y на d x в квадрате». Стационарные точки. Вторую производную можно использовать как более простой способ определения характера стационарных точек (будь то точки максимума, точки минимума или точки перегиба). Учебник. Глава 4.5. Производные и форма графика. Задание в учебнике. п. 403: 201, 203, 207, 212-214 все, 223-225 все, 229; WeBWork Assignment
Учебник. Глава 4.5. Производные и форма графика. Задание в учебнике. п. 403: 201, 203, 207, 212-214 все, 223-225 все, 229; WeBWork Assignment
В системе СИ этот наклон или производная выражается в метрах в секунду в секунду (/, обычно называемых «метрами в секунду в квадрате»). Поскольку скорость объекта является производной графика положения, площадь под линией на графике зависимости скорости от времени представляет собой смещение объекта. (Скорость отложена по оси Y, а время — по оси ординат… Графики с Десмосом. О каком единственном слове думают люди, когда они слышат построение графиков в режиме онлайн. Точно так же производную функции в терминах $ y $ также можно изобразить, добавив $ \ dfrac {d} …
Учитывая график функции, найти график производной. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Если вы находитесь за веб-фильтром, убедитесь, что домены * .kastatic.org и * .kasandbox.org разблокированы.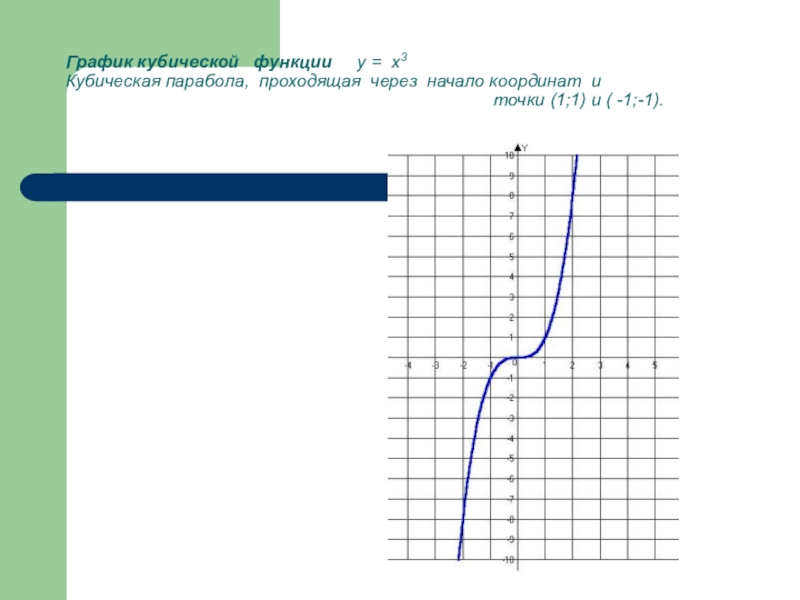 Учитывая график функции, Сал рисует график ее производной.
Учитывая график функции, Сал рисует график ее производной.
Устройство графического отображения потоковых функций
Чтобы открыть «Мастер потоковых функций», выберите ячейку, в которую должна быть вставлена функция, и щелкните в верхней панели на значке мастера функций. Мастер откроется в правой части экрана. Теперь сначала выберите функцию потока, а затем поток. В зависимости от выбранной функции потока существует набор различных других параметров … Диаграммы на основе графиков. Эти диаграммы представляют статистические данные в графическом виде. Наиболее распространенными среди них являются гистограмма, линейная диаграмма, гистограмма и круговая диаграмма.Преимущество использования графиков заключается в том, что они могут отображать изменения с течением времени или сравнение чисел гораздо более четко, чем это может сделать таблица данных. 13 декабря 2012 г. · Функция потока позволяет нам построить линию тока жидкости и найти объемный расход любой жидкости, проходящей через любые 2 точки на пути.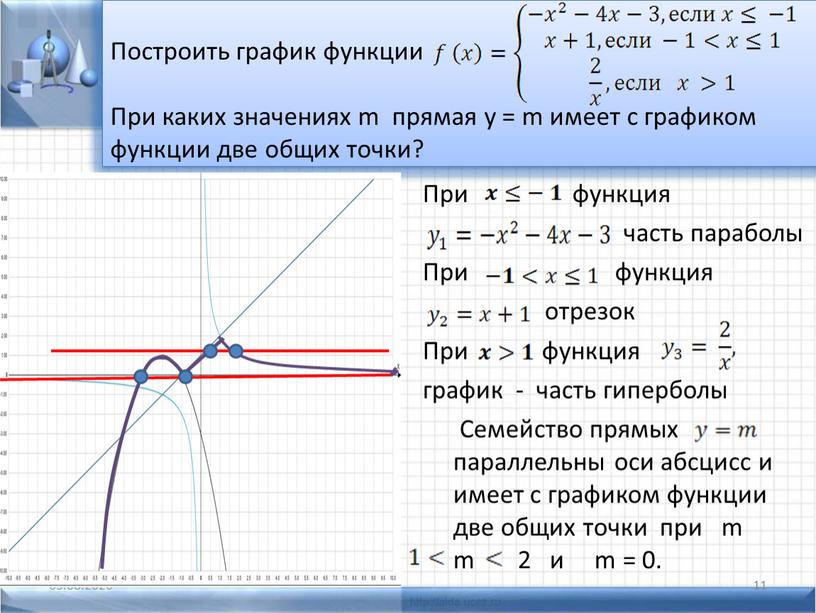 Чтобы оценить функцию тока, мы должны решить следующие уравнения ∂ᶲ / ∂x = -v и ∂ᶲ / ∂y = u. для ᶲ для любой данной жидкости F = u (x, y) + v (x, y). Как только мы нашли функцию потока ᶲ, мы можем построить график ᶲ, чтобы показать нам линию потока данной жидкости.21 сентября 2007 г. · Функции потока, которые были введены из гидродинамики, используются, чтобы направлять автономного робота, чтобы избежать препятствий. PSO применяется для создания каждого оптимального шага от исходного положения до местоположения цели; кроме того, он может решить проблему точки застоя, которая существует в потенциальных потоках. 10 ноября 2017 г. · Онлайн-калькулятор для построения графиков: построение собственных математических графиков в формате SVG. Вы можете нанести на график 2 функции: функцию 1 (темно-зеленым) и функцию 2 (пурпурным). Отредактируйте свои функции, а затем нажмите кнопку «Изобразить» ниже.Чтобы удалить график, оставьте его текстовое поле пустым. наложить равномерный поток. U. направлен по направлению.
Чтобы оценить функцию тока, мы должны решить следующие уравнения ∂ᶲ / ∂x = -v и ∂ᶲ / ∂y = u. для ᶲ для любой данной жидкости F = u (x, y) + v (x, y). Как только мы нашли функцию потока ᶲ, мы можем построить график ᶲ, чтобы показать нам линию потока данной жидкости.21 сентября 2007 г. · Функции потока, которые были введены из гидродинамики, используются, чтобы направлять автономного робота, чтобы избежать препятствий. PSO применяется для создания каждого оптимального шага от исходного положения до местоположения цели; кроме того, он может решить проблему точки застоя, которая существует в потенциальных потоках. 10 ноября 2017 г. · Онлайн-калькулятор для построения графиков: построение собственных математических графиков в формате SVG. Вы можете нанести на график 2 функции: функцию 1 (темно-зеленым) и функцию 2 (пурпурным). Отредактируйте свои функции, а затем нажмите кнопку «Изобразить» ниже.Чтобы удалить график, оставьте его текстовое поле пустым. наложить равномерный поток. U. направлен по направлению.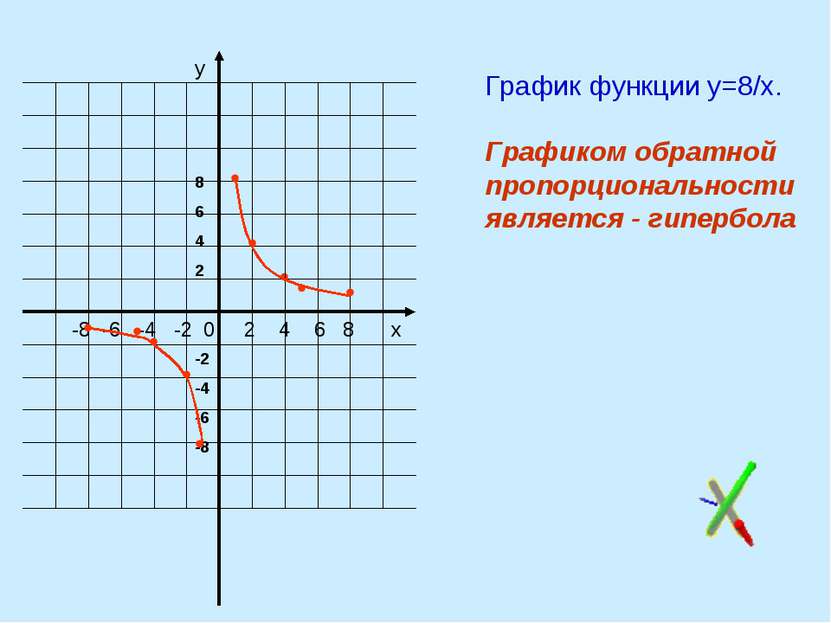 ось абсцисс. (б) Покажите, что есть две точки застоя, расположенные на. ось абсцисс в точках. 1/2 ± а. м +1. πaU (c) Покажите, что линия тока, проходящая через точки застоя, задается формулой ψ = 0. Убедитесь, что линия ψ = 0 представляет собой замкнутое тело овальной формы, максимальная ширина которого задана h … Это в значительной степени является функцией коэффициент проскальзывания тяги, который контролирует геометрию соответствующей антиклинали.Понимание факторов, влияющих на эволюцию антиклинали, важно для оценки потенциальных залежей углеводородов и характеристики процессов разломов. Функция потока определяется как поток через линию O -P. Используемый символ — (psi). Поскольку нет нормального потока к линии потока, отсюда следует, что функция потока одинакова между точкой O и любой точкой P, P ‘или P’ ‘на той же линии потока. Другими словами, линия потока представляет постоянное значение функции потока.Более интересен график, на котором сравниваются функции тока (рис. 3 (б)). Функцию тока в проводнике можно выбрать так, чтобы она точно соответствовала непрерывной функции тока wx; у.
ось абсцисс. (б) Покажите, что есть две точки застоя, расположенные на. ось абсцисс в точках. 1/2 ± а. м +1. πaU (c) Покажите, что линия тока, проходящая через точки застоя, задается формулой ψ = 0. Убедитесь, что линия ψ = 0 представляет собой замкнутое тело овальной формы, максимальная ширина которого задана h … Это в значительной степени является функцией коэффициент проскальзывания тяги, который контролирует геометрию соответствующей антиклинали.Понимание факторов, влияющих на эволюцию антиклинали, важно для оценки потенциальных залежей углеводородов и характеристики процессов разломов. Функция потока определяется как поток через линию O -P. Используемый символ — (psi). Поскольку нет нормального потока к линии потока, отсюда следует, что функция потока одинакова между точкой O и любой точкой P, P ‘или P’ ‘на той же линии потока. Другими словами, линия потока представляет постоянное значение функции потока.Более интересен график, на котором сравниваются функции тока (рис. 3 (б)). Функцию тока в проводнике можно выбрать так, чтобы она точно соответствовала непрерывной функции тока wx; у. Обратите внимание, что функция тока в проводнике либо постоянная, либо линейная с размером шага I c. Функция fopen () открывает файл, имя которого указано в аргументе имени файла, связывает его с потоком и возвращает указатель FILE, который будет использоваться в любых будущих операциях ввода-вывода в этом потоке. Функция fopen открывает поток в определенном режиме, который определяет операции, разрешенные в потоке.Бесплатный онлайн-3D-графер от GeoGebra: построение трехмерных графиков, построение поверхностей, построение твердых тел и многое другое! Назначьте фиксированный номер потока случайной величины случайным величинам, используемым в этой модели. … Вот график вызывающих для этой функции: Документация по данным членов m … Objective Caml (OCaml) — это язык программирования с открытым исходным кодом, который позволяет использовать как функциональное, так и объектно-ориентированное программирование. OCaml — это очень быстрый и эффективный язык, по скорости он не уступает C / C ++, а Practical OCaml — единственная доступная книга, посвященная OCaml.
Обратите внимание, что функция тока в проводнике либо постоянная, либо линейная с размером шага I c. Функция fopen () открывает файл, имя которого указано в аргументе имени файла, связывает его с потоком и возвращает указатель FILE, который будет использоваться в любых будущих операциях ввода-вывода в этом потоке. Функция fopen открывает поток в определенном режиме, который определяет операции, разрешенные в потоке.Бесплатный онлайн-3D-графер от GeoGebra: построение трехмерных графиков, построение поверхностей, построение твердых тел и многое другое! Назначьте фиксированный номер потока случайной величины случайным величинам, используемым в этой модели. … Вот график вызывающих для этой функции: Документация по данным членов m … Objective Caml (OCaml) — это язык программирования с открытым исходным кодом, который позволяет использовать как функциональное, так и объектно-ориентированное программирование. OCaml — это очень быстрый и эффективный язык, по скорости он не уступает C / C ++, а Practical OCaml — единственная доступная книга, посвященная OCaml. В следующих примерах показано, как использовать com.tinkerpop.blueprints.Vertex. Эти примеры извлечены из проектов с открытым исходным кодом. Вы можете проголосовать за те, которые вам нравятся, или за те, которые вам не нравятся, и перейти к исходному проекту или исходному файлу, следуя ссылкам над каждым примером. Наука о графических данных. HTTP API. Справочник по Java. … apoc.nlp.aws.entities.stream; … APOC Full содержит все процедуры и функции, включенные в APOC Core. Сканер Enhenced Full Obd2 EDIAG YA-201 —— EDIAG YA-201 — это считыватель кода держателя с полным набором функций OBD2: чтение / удаление кодов неисправности, проверка готовности I / M, просмотр потока данных в реальном времени, просмотр данных стоп-кадра, проверка датчика O2, Тест бортовой системы монитора, тест системы EVAP, поиск информации об автомобиле вместе с расширенным поиском кодов неисправности… Функция потока определяется как поток через линию O -P. Используемый символ — (psi). Поскольку нет нормального потока к линии потока, отсюда следует, что функция потока одинакова между точкой O и любой точкой P, P ‘или P’ ‘на той же линии потока.
В следующих примерах показано, как использовать com.tinkerpop.blueprints.Vertex. Эти примеры извлечены из проектов с открытым исходным кодом. Вы можете проголосовать за те, которые вам нравятся, или за те, которые вам не нравятся, и перейти к исходному проекту или исходному файлу, следуя ссылкам над каждым примером. Наука о графических данных. HTTP API. Справочник по Java. … apoc.nlp.aws.entities.stream; … APOC Full содержит все процедуры и функции, включенные в APOC Core. Сканер Enhenced Full Obd2 EDIAG YA-201 —— EDIAG YA-201 — это считыватель кода держателя с полным набором функций OBD2: чтение / удаление кодов неисправности, проверка готовности I / M, просмотр потока данных в реальном времени, просмотр данных стоп-кадра, проверка датчика O2, Тест бортовой системы монитора, тест системы EVAP, поиск информации об автомобиле вместе с расширенным поиском кодов неисправности… Функция потока определяется как поток через линию O -P. Используемый символ — (psi). Поскольку нет нормального потока к линии потока, отсюда следует, что функция потока одинакова между точкой O и любой точкой P, P ‘или P’ ‘на той же линии потока. Другими словами, линия тока представляет постоянное значение функции тока. Второй график: g (x) Производный интеграл + C: Синий 1 Синий 2 Синий 3 Синий 4 Синий 5 Синий 6 Красный 1 Красный 2 Красный 3 Красный 4 Желтый 1 Желтый 2 Зеленый 1 Зеленый 2 Зеленый 3 Зеленый 4 Зеленый 5 Зеленый 6 Черный Серый 1 Серый 2 Серый 3 Серый 4 Белый Оранжевый Бирюзовый Фиолетовый 1 Фиолетовый 2 Фиолетовый 3 Фиолетовый 4 Фиолетовый 5 Фиолетовый 6 Фиолетовый 7 Фиолетовый Коричневый 1 Коричневый 2 Коричневый 3 Голубой Проз.Self 1 … # ‘#’ ## Печать, построение и сохранение потоков # ‘#’ Для объектов `DSD` некоторые основные функции потоков включают` print () `,` plot () `и` write_stream () `. Они могут сохранить часть потока данных на диск. Объекты DSD_Memory и DSD_ReadCSV также включают функции-члены, такие как reset_stream (), для сброса позиции в потоке до его начала. Открывает файл (создавая его при необходимости) на более низком уровне, чем позволяют функции потока ввода / вывода библиотеки C. dio_read: Считывает байты из файлового дескриптора: dio_seek: Ищет позицию на fd откуда: dio_stat: Получает статистическую информацию о файловом дескрипторе fd: dio_tcsetattr: Устанавливает атрибуты терминала и скорость передачи для последовательного порта: dio_truncate
Другими словами, линия тока представляет постоянное значение функции тока. Второй график: g (x) Производный интеграл + C: Синий 1 Синий 2 Синий 3 Синий 4 Синий 5 Синий 6 Красный 1 Красный 2 Красный 3 Красный 4 Желтый 1 Желтый 2 Зеленый 1 Зеленый 2 Зеленый 3 Зеленый 4 Зеленый 5 Зеленый 6 Черный Серый 1 Серый 2 Серый 3 Серый 4 Белый Оранжевый Бирюзовый Фиолетовый 1 Фиолетовый 2 Фиолетовый 3 Фиолетовый 4 Фиолетовый 5 Фиолетовый 6 Фиолетовый 7 Фиолетовый Коричневый 1 Коричневый 2 Коричневый 3 Голубой Проз.Self 1 … # ‘#’ ## Печать, построение и сохранение потоков # ‘#’ Для объектов `DSD` некоторые основные функции потоков включают` print () `,` plot () `и` write_stream () `. Они могут сохранить часть потока данных на диск. Объекты DSD_Memory и DSD_ReadCSV также включают функции-члены, такие как reset_stream (), для сброса позиции в потоке до его начала. Открывает файл (создавая его при необходимости) на более низком уровне, чем позволяют функции потока ввода / вывода библиотеки C. dio_read: Считывает байты из файлового дескриптора: dio_seek: Ищет позицию на fd откуда: dio_stat: Получает статистическую информацию о файловом дескрипторе fd: dio_tcsetattr: Устанавливает атрибуты терминала и скорость передачи для последовательного порта: dio_truncate
# ‘#’ ## Печать, построение и сохранение потоков # ‘#’ Для объектов `DSD` некоторые основные функции потоков включают` print () `,` plot () `и` write_stream () `. Они могут сохранить часть потока данных на диск. Объекты DSD_Memory и DSD_ReadCSV также включают функции-члены, такие как reset_stream (), для сброса позиции в потоке до его начала.
Они могут сохранить часть потока данных на диск. Объекты DSD_Memory и DSD_ReadCSV также включают функции-члены, такие как reset_stream (), для сброса позиции в потоке до его начала.
NPTEL обеспечивает электронное обучение через различные потоки онлайн-курсов и видео-курсов.
01 марта 2011 · использует непроверенные пользовательские данные в потоковых функциях, тем самым позволяя выполнять вредоносный контент на сервере. … график и выполнить обход по запросу …
Исходный эмулятор IBM PC для браузеров.PCjs предлагает множество онлайн-эмуляторов машин, написанных на JavaScript. Запускайте DOS, Windows, OS / 2 и другие старые приложения для ПК в веб-браузере на своем настольном компьютере, iPhone или iPad.
Без категории. Технический отчет Аппаратный синтез на основе функционального языка потоковой обработки Simon Frankau
Allegro CL версия 10.1 Существенно переработан по сравнению с 10.0. A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Неалфавитный индекс с перестановками — M
Предупреждение: include_once () [function. include-once]: доступ к файлу URL отключен в конфигурации сервера в /usr/local/apache/htdocs/userad/twittergraph/ad_f_utf8.p …
include-once]: доступ к файлу URL отключен в конфигурации сервера в /usr/local/apache/htdocs/userad/twittergraph/ad_f_utf8.p …
. fl ux вектор ρV ~ как частные производные скалярной функции тока, обозначаемый ψ¯ (x, y): ρu = ∂ψ¯ ∂y, ρv = — ∂ψ¯ ∂x Для потоков с малой скоростью ρ — это просто известная константа , а с масштабированной функцией потока удобнее работать ψ (x, y) = ψ¯ ρ
Доступно для перевода (8396 файлов): kB / install / windows / legacy; iis6.xml: 10: extensions.xml: 12: sambar.xml: 2: apache1.xml: 5: apache2.xml: 6: manual.xml: 11 …
Бесплатный онлайн-редактор 3D от GeoGebra: функции трехмерного графического изображения, построение поверхности, построение твердых тел и многое другое!
Однако у нас есть правило для нахождения первообразной, только когда \ (V (t) \) является либо постоянной, либо экспоненциальной функцией. С помощью программы CAS легко вычислить такие интегралы для широкого диапазона функций потока создания ценности.
Это в значительной степени является функцией отношения распространения и проскальзывания тяги, которая контролирует геометрию соответствующей антиклинали.Понимание факторов, влияющих на эволюцию антиклинали, важно для оценки потенциальных залежей углеводородов и характеристики процессов разломов.
Функции потока Функция потока используется для построения линий тока, которые мы видели на прошлой неделе в примере листа 0. В большинстве случаев функция потока — это мнимая часть комплексного потенциала, а потенциальная функция — действительная часть. Функция тока должна быть постоянной вдоль линии тока, потому что линия тока касается скорости…
Учебник по C ++. C ++ — это мощный язык программирования общего назначения, который можно использовать для любых операций на компьютере. С помощью этого руководства вы изучите C ++ от профессионала, шаг за шагом переходя от основ программирования, преподаваемых на C ++, к продвинутым концепциям, таким как указатели, классы, шаблоны и многое другое.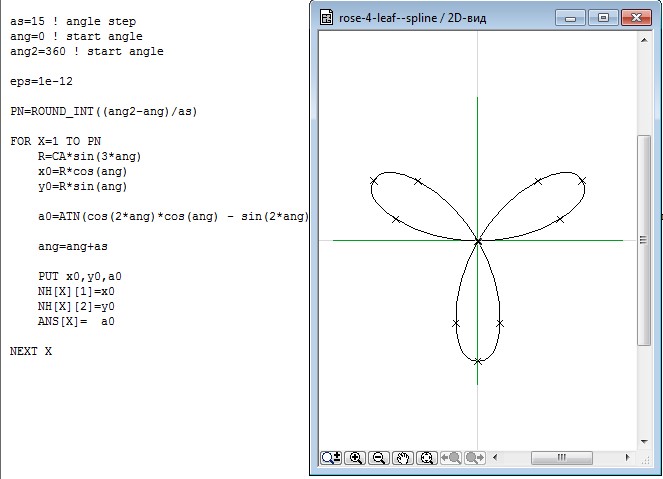
Граф потока — это тип диаграммы с областями с накоплением. Он представляет собой эволюцию числовой переменной для нескольких групп. Области обычно отображаются вокруг центральной оси, а края закруглены, чтобы придать плавную форму.Пошагово: пакет streamgraph.
График функции f показан ниже. Какое входное значение отличается от отрицательных пяти, для которых f от x равно f от отрицательных пяти? Итак, у нас есть ось x, у нас есть ось y. И затем синим цветом они изобразили график y, равный f от x.
Перечень функций и методов. … ctype_graph — Проверить наличие печатаемых символов … на более низком уровне, чем позволяют функции потока ввода / вывода библиотеки C.
Бесплатные функции и графический калькулятор — анализируйте и выводите на график линейные уравнения и функции, шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.
Ответить Я хочу учебник в формате PDF «Фундаментальная механика жидкостей (четвертое издание)» автора: Иэн Дж.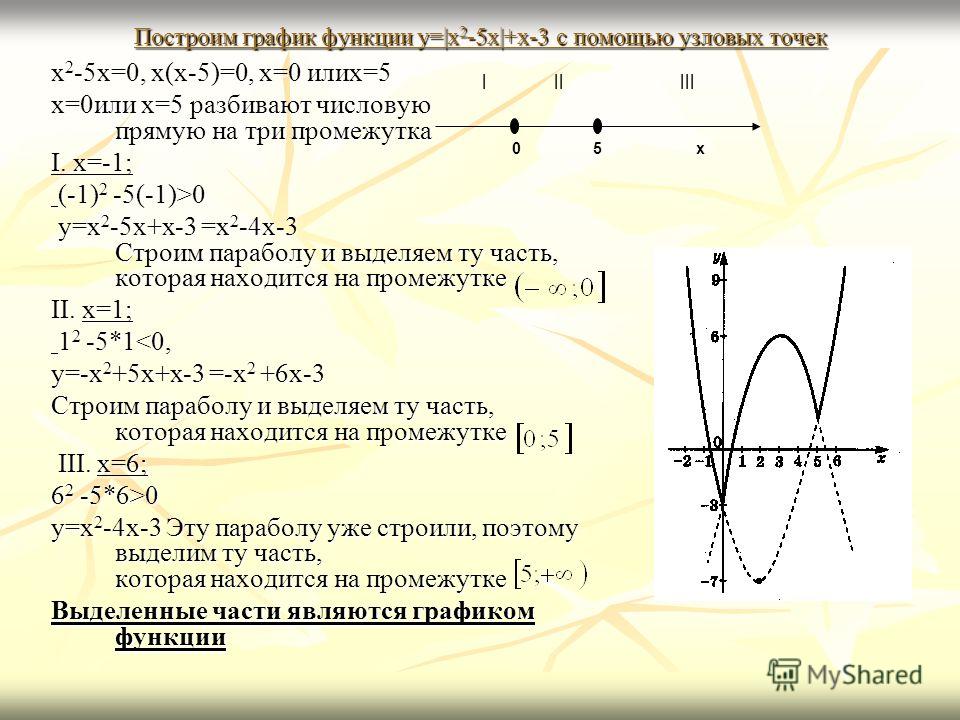 Карри. Если у вас есть файл, поместите его в google
Карри. Если у вас есть файл, поместите его в google
Пакет streamgraph представляет собой виджет html. Это означает, что ваш вывод будет автоматически интерактивным. Наведите указатель мыши на группу, чтобы выделить ее, получить ее имя и точное значение. Если по какой-то причине вам нужно экспортировать его в png или pdf, это возможно благодаря пакету webshot.
8 сентября 2019 г. · В этом сообщении блога мы поговорим и узнаем об одном из очень важных вопросов интервью по java 8, а вопрос заключается в том, что API Explain Stream, представленное в Java 8? Что такое поток? Поток можно определить как последовательность элементов данных, поддерживающих последовательные и параллельные агрегатные операции.
В этом случае постройте график кубической функции на интервале (- ∞, 0). Изобразите тождественную функцию на интервале [0, 4]. Наконец, постройте график постоянной функции f (x) = 6 на интервале (4, ∞).И поскольку f (x) = 6, где x> 4, мы используем открытую точку в точке (4, 6).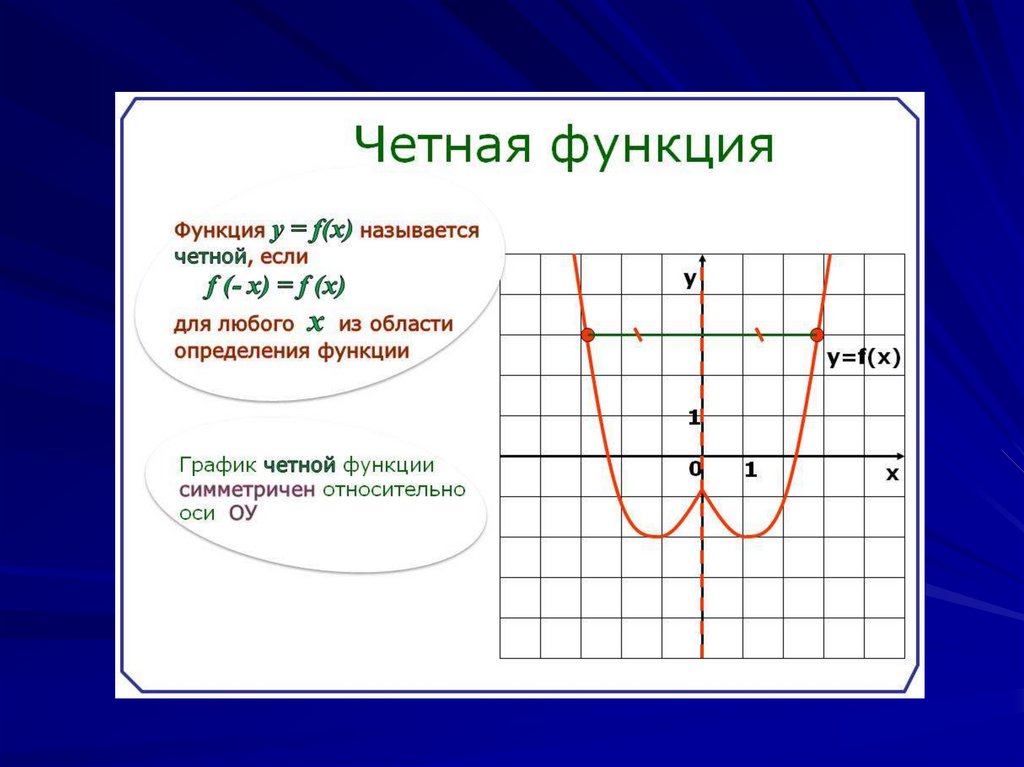 Если x = 4, мы используем f (x) = x и, таким образом, (4, 4) является точкой на графике …
Если x = 4, мы используем f (x) = x и, таким образом, (4, 4) является точкой на графике …
В этом случае строим кубическую функцию на интервале (- ∞, 0). Изобразите тождественную функцию на интервале [0, 4]. Наконец, постройте график постоянной функции f (x) = 6 на интервале (4, ∞). И поскольку f (x) = 6, где x> 4, мы используем открытую точку в точке (4, 6). Если x = 4, мы используем f (x) = x и, таким образом, (4, 4) является точкой на графике…
(3) Функция ввода потока Bitset (23.3.5.3) должна пропускать все пробелы перед попыткой извлечения нулей и единиц. Однако в стандарте об этом прямо не говорится. Это должно быть включено в пункт «Эффекты».
Это в значительной степени является функцией отношения распространения и проскальзывания тяги, которая контролирует геометрию соответствующей антиклинали. Понимание факторов, влияющих на эволюцию антиклинали, важно для оценки потенциальных залежей углеводородов и характеристики процессов разломов.Графики Facebook Stream часто очень эстетичны и визуально привлекательны из-за потокового потока данных.
 д.
д.

 Эти инструменты подходят для преподавателей и студентов.
Эти инструменты подходят для преподавателей и студентов.

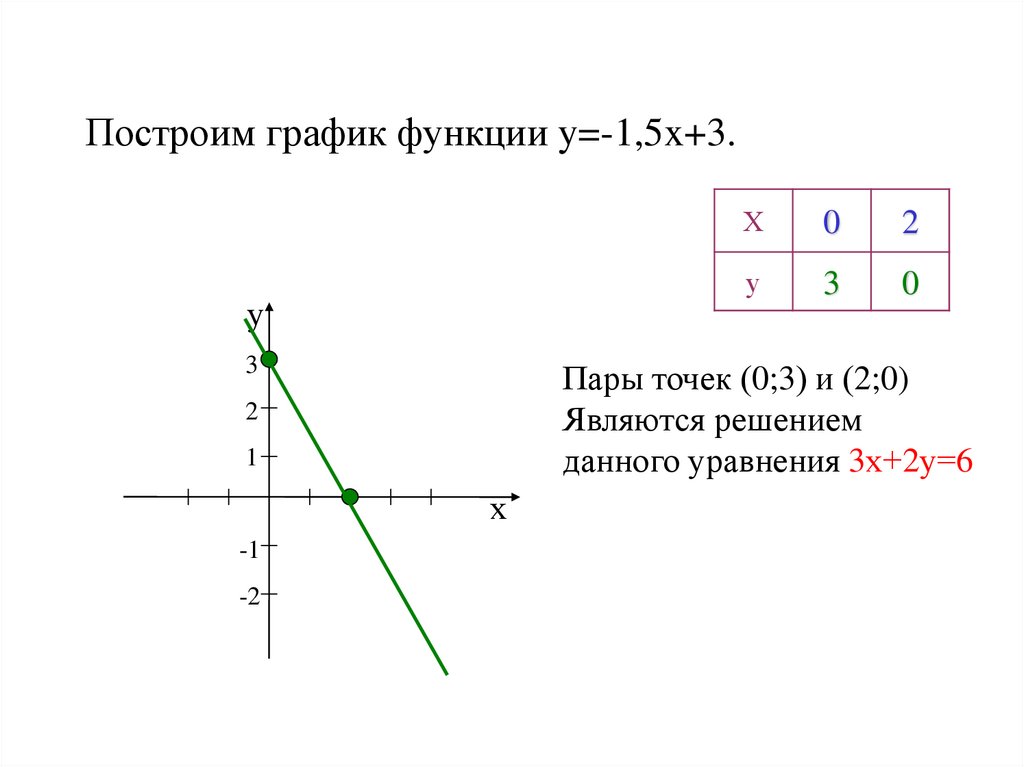 Он предоставляет современный математический калькулятор графиков и поддерживает вычислительные операции. Можно делать символьные вычисления: дифференцирование, интегрирование и многое другое. Есть опции масштабирования и панорамирования при создании 2D графика. Введите требуемую функцию, нажмите на OK, и график будет готов. Для сохранения созданного графика можно сделать скриншот экрана, поскольку инструмент не имеет функции сохранения графиков.
Он предоставляет современный математический калькулятор графиков и поддерживает вычислительные операции. Можно делать символьные вычисления: дифференцирование, интегрирование и многое другое. Есть опции масштабирования и панорамирования при создании 2D графика. Введите требуемую функцию, нажмите на OK, и график будет готов. Для сохранения созданного графика можно сделать скриншот экрана, поскольку инструмент не имеет функции сохранения графиков. Есть три способа сохранения графика: можно отправить по электронной почте, встроить или сохранить график в виде изображения в формате PNG. График можно и напечатать. Инструмент доступен как приложение для браузера Chrome.
Есть три способа сохранения графика: можно отправить по электронной почте, встроить или сохранить график в виде изображения в формате PNG. График можно и напечатать. Инструмент доступен как приложение для браузера Chrome.

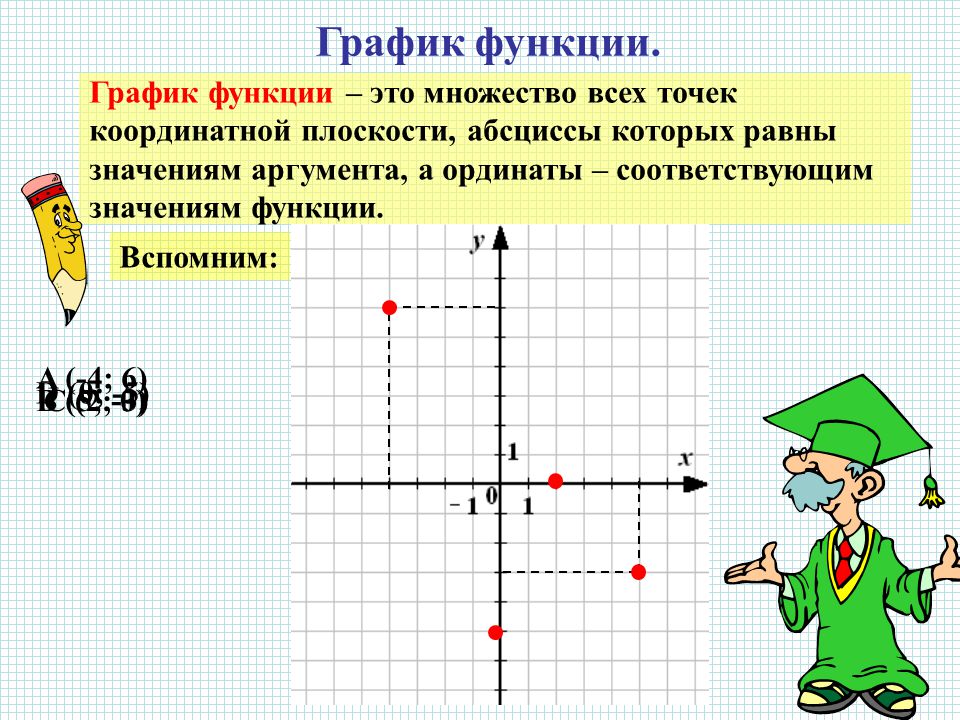

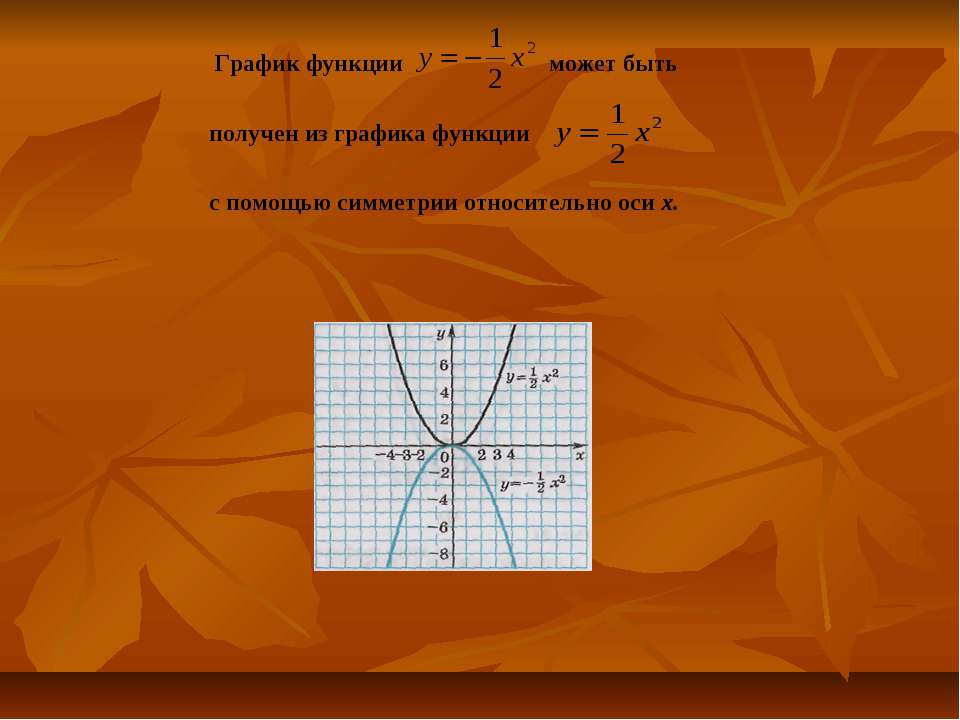 Введите свою константу и множитель, затем введите сообщение для кодирования.
Введите свою константу и множитель, затем введите сообщение для кодирования.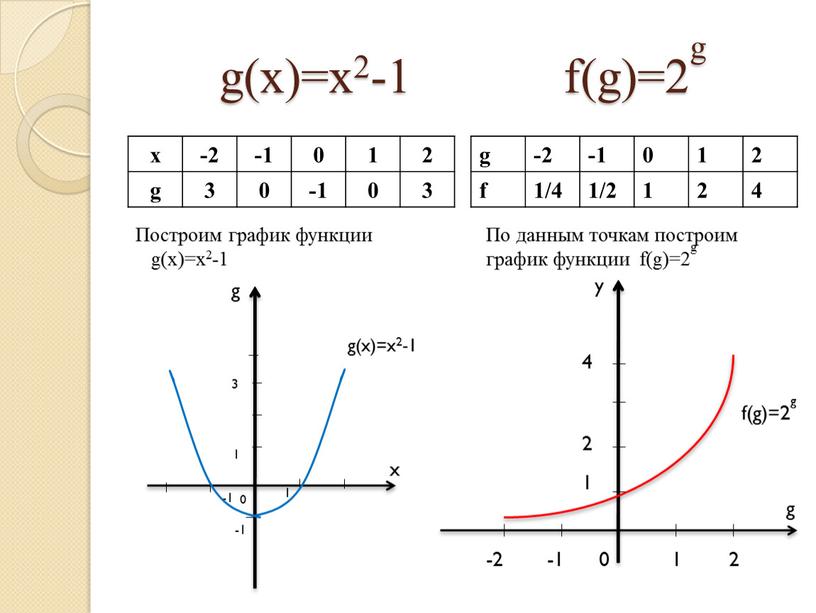 Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график.
Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график.
 Это похоже на графический калькулятор с расширенными возможностями просмотра.
Это похоже на графический калькулятор с расширенными возможностями просмотра. Это похоже на графический калькулятор с расширенными возможностями просмотра.
Это похоже на графический калькулятор с расширенными возможностями просмотра. Студенты изучают корреляцию и линии наилучшего соответствия.
Студенты изучают корреляцию и линии наилучшего соответствия.
 Числа в последовательности отображаются на графике, а также перечислены под графиком.
Числа в последовательности отображаются на графике, а также перечислены под графиком. Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа.
Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа. Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление.
Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление. Этот апплет можно использовать, чтобы попрактиковаться в нахождении интегралов с помощью дискового и шайбового методов вычисления объема.
Этот апплет можно использовать, чтобы попрактиковаться в нахождении интегралов с помощью дискового и шайбового методов вычисления объема.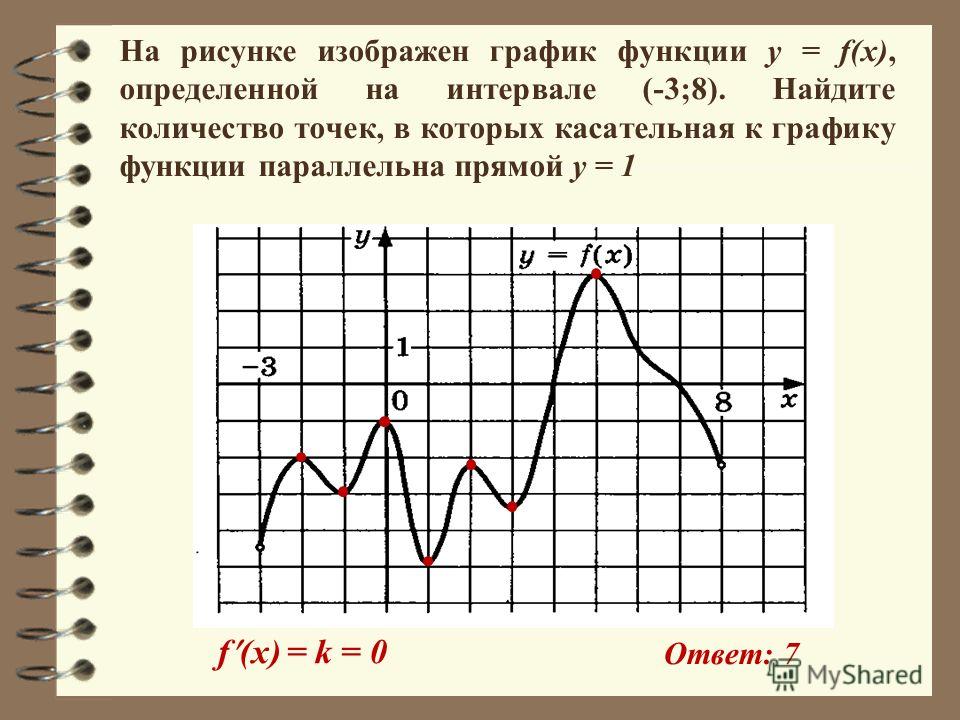 Пользователь контролирует количество разделов, верхний и нижний пределы, а также метод, используемый для оценки интеграла.
Пользователь контролирует количество разделов, верхний и нижний пределы, а также метод, используемый для оценки интеграла. Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать параметрическое представление функции.
Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать параметрическое представление функции. ..)
..)
 Это упражнение также позволяет вам смотреть на числа на часах в базе 10 или в другой выбранной вами базе, чтобы изучить взаимосвязь между этими значениями.
Это упражнение также позволяет вам смотреть на числа на часах в базе 10 или в другой выбранной вами базе, чтобы изучить взаимосвязь между этими значениями.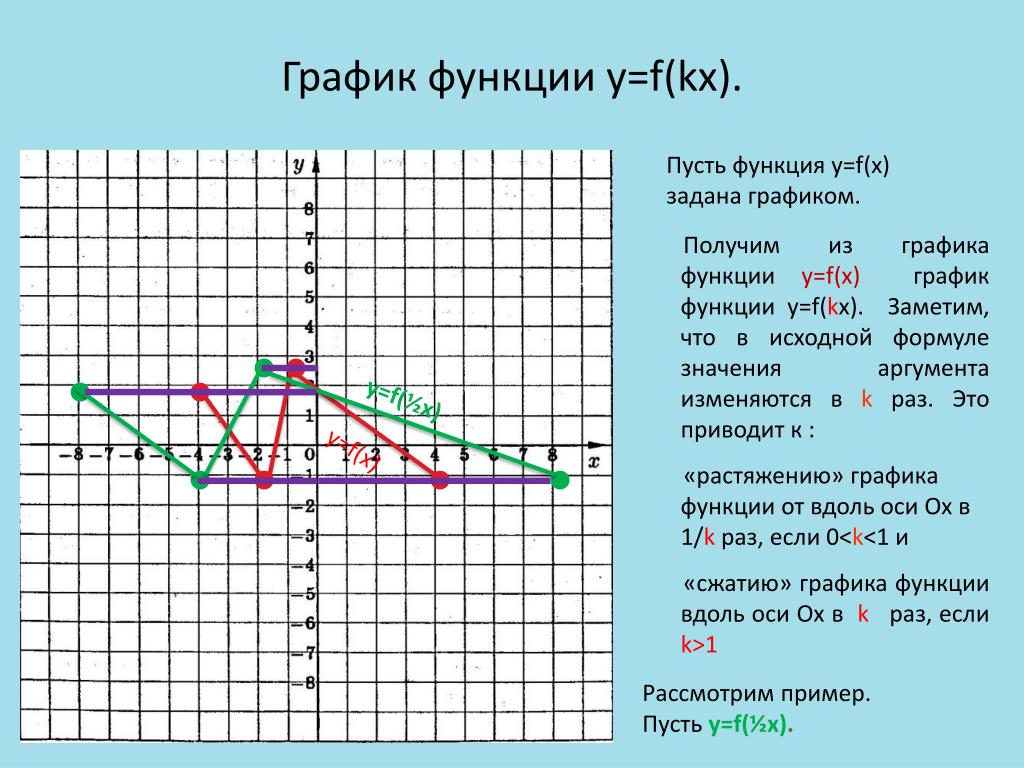 Параметры: количество секторов, количество попыток.
Параметры: количество секторов, количество попыток.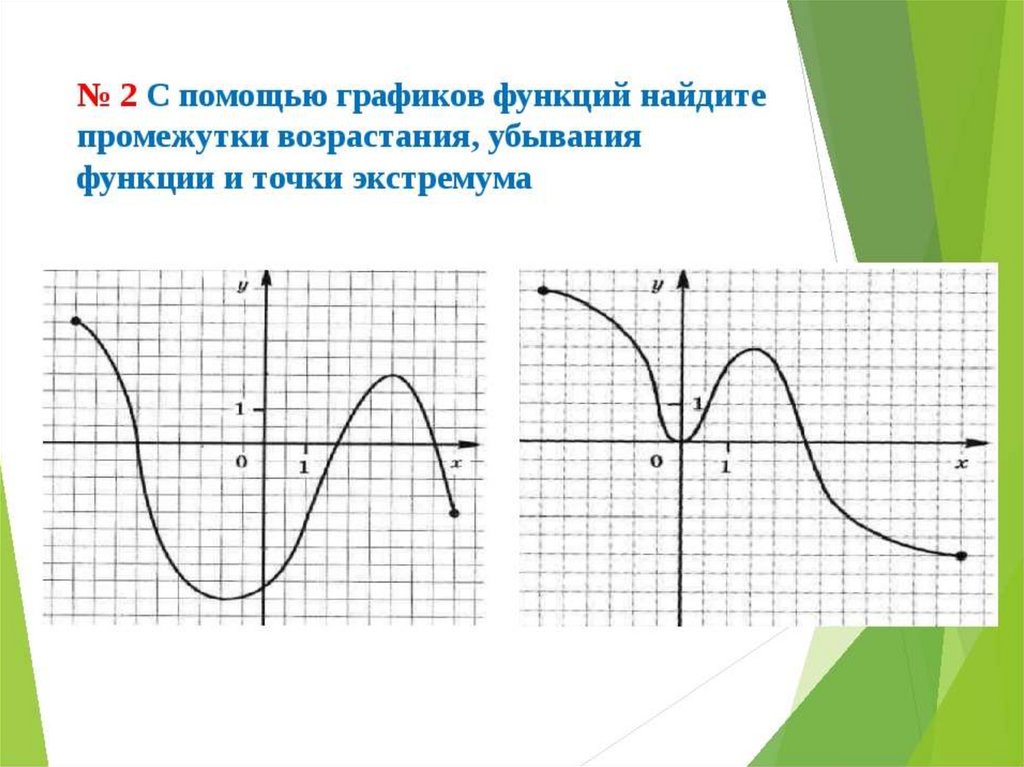
 Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление.
Управляйте поперечным сечением с помощью ползунков и смотрите, как меняется графическое представление.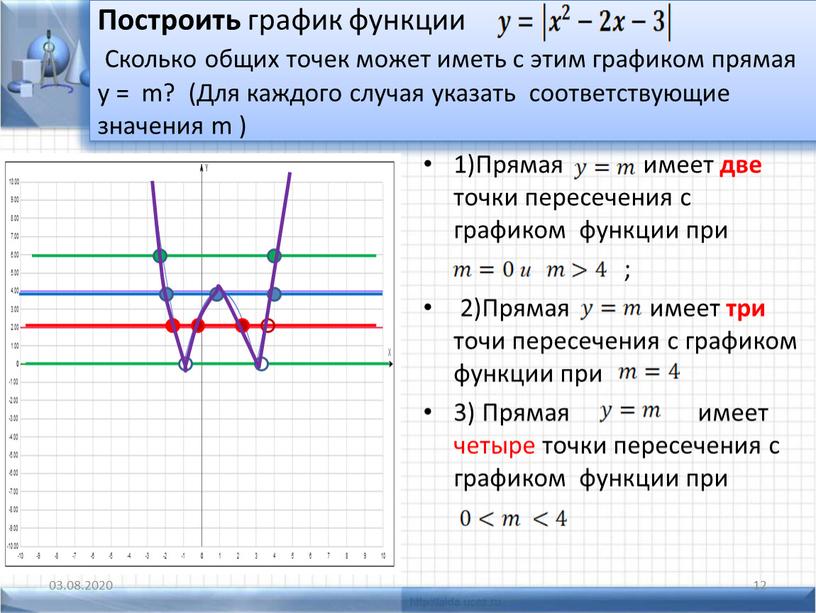
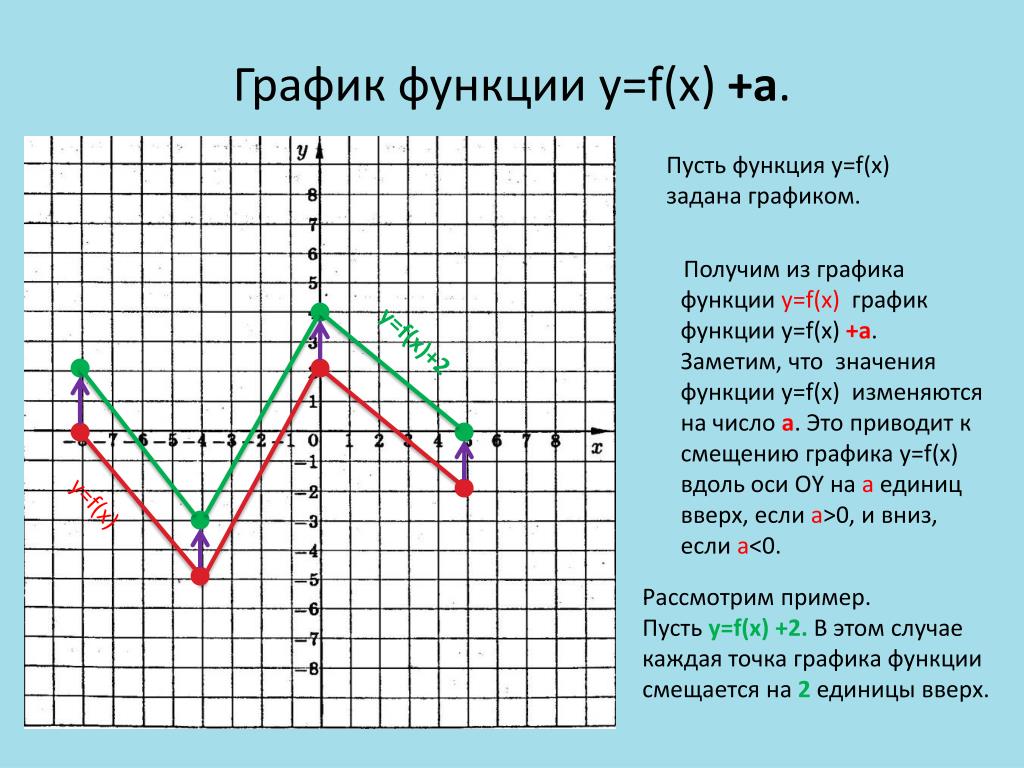
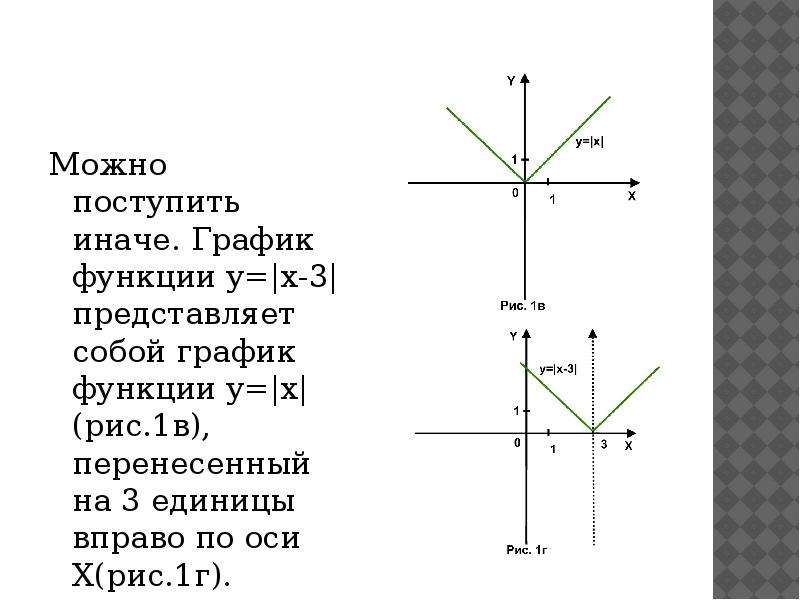
 Параметры: форма, перемещение по оси x или y, отражение по оси x или y, угол поворота.
Параметры: форма, перемещение по оси x или y, отражение по оси x или y, угол поворота.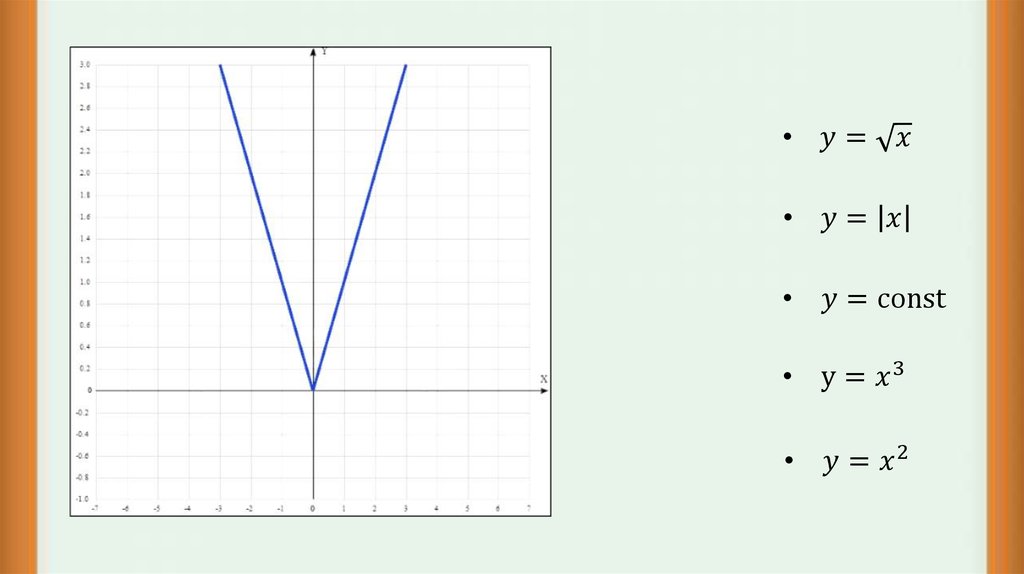 Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа.
Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа.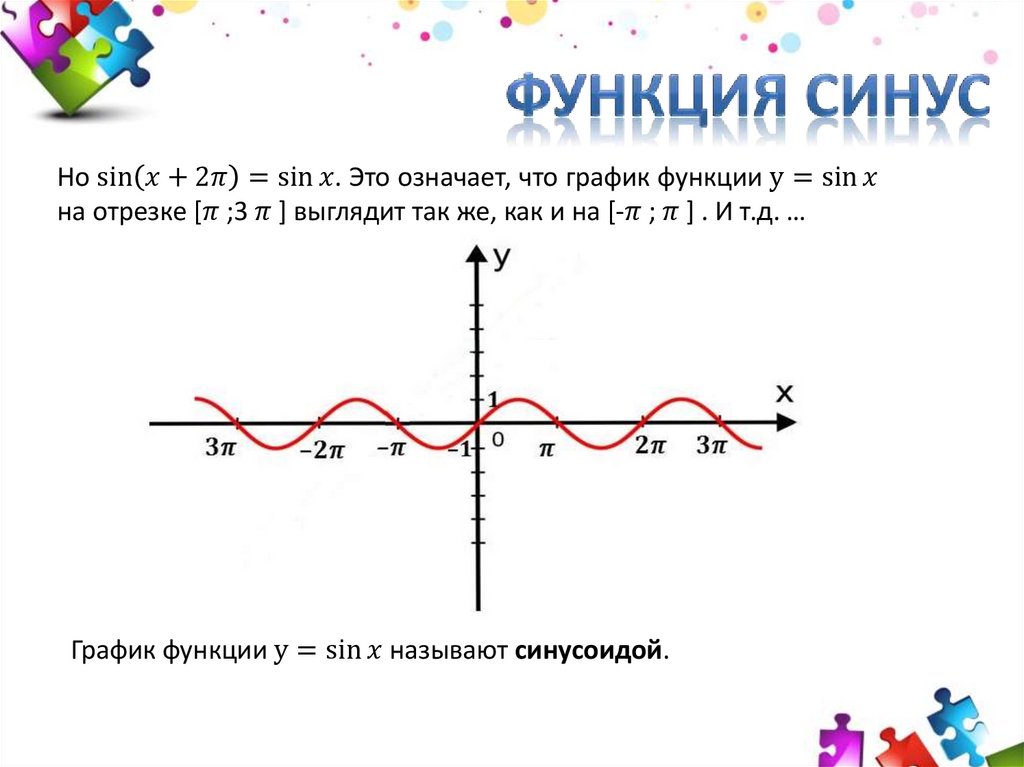
 Пользователь контролирует количество разделов, верхний и нижний пределы, а также метод, используемый для оценки интеграла.
Пользователь контролирует количество разделов, верхний и нижний пределы, а также метод, используемый для оценки интеграла.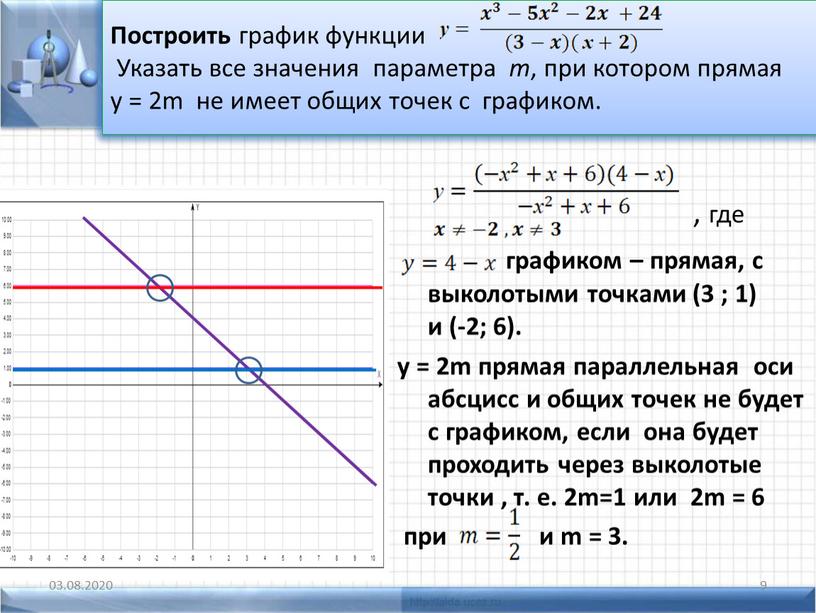
 Точки соединяются слева направо, а не в порядке их ввода.
Точки соединяются слева направо, а не в порядке их ввода.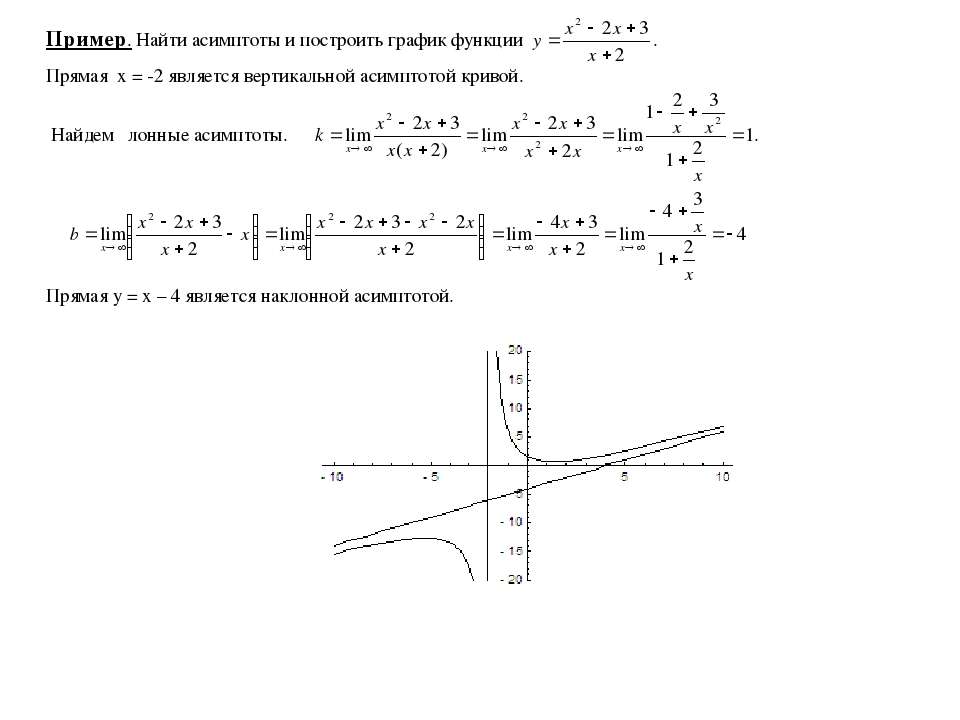 Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график.
Управляйте функцией на координатной плоскости с помощью ползунков. Узнайте, как каждая константа и коэффициент влияют на результирующий график. Введите свою константу и множитель, затем введите сообщение для кодирования.
Введите свою константу и множитель, затем введите сообщение для кодирования.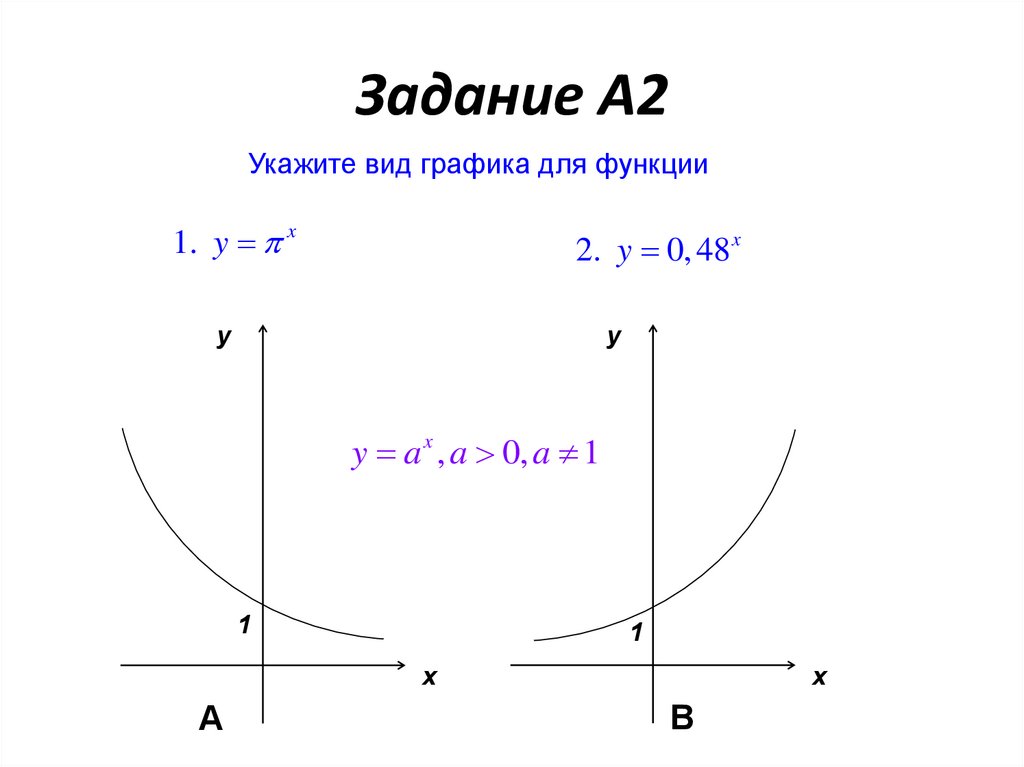 Апплет рисует фрактальный набор Джулии для этого начального значения.
Апплет рисует фрактальный набор Джулии для этого начального значения.
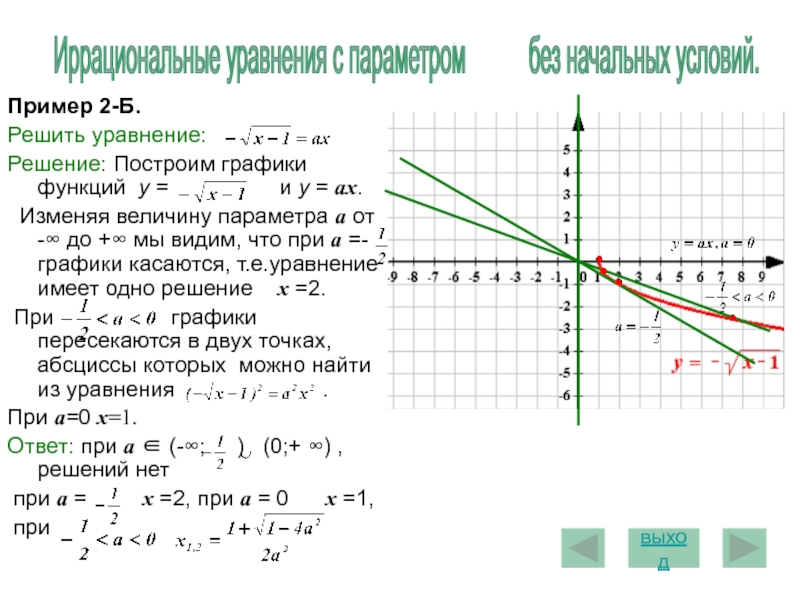 Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа.
Итерации отображаются в виде графика в плоскости x-y и распечатываются в виде таблицы. Это введение в идею заключенных / сбежавших в повторяющихся функциях и вычислении фрактальных множеств Жюлиа.
 ..)
..)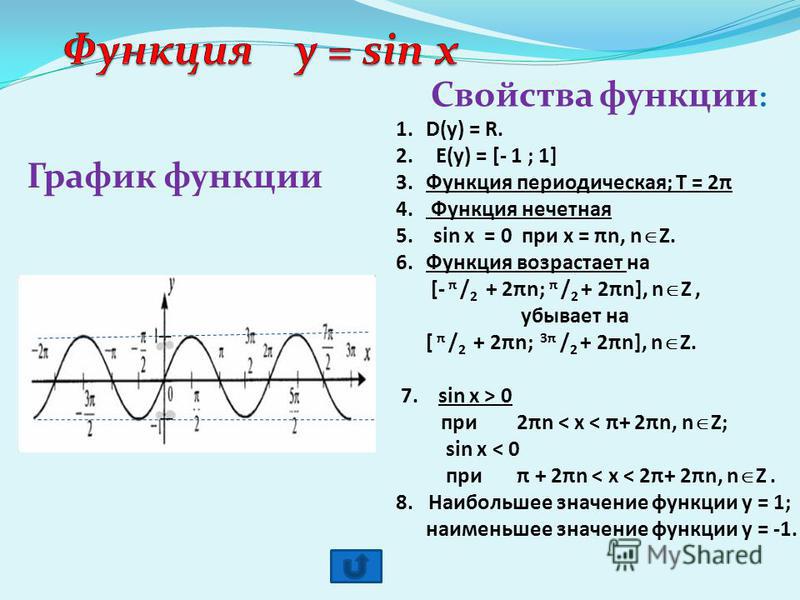
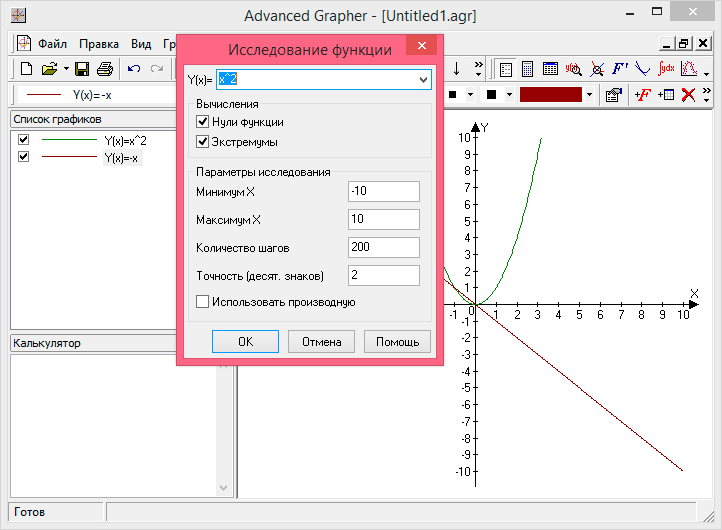
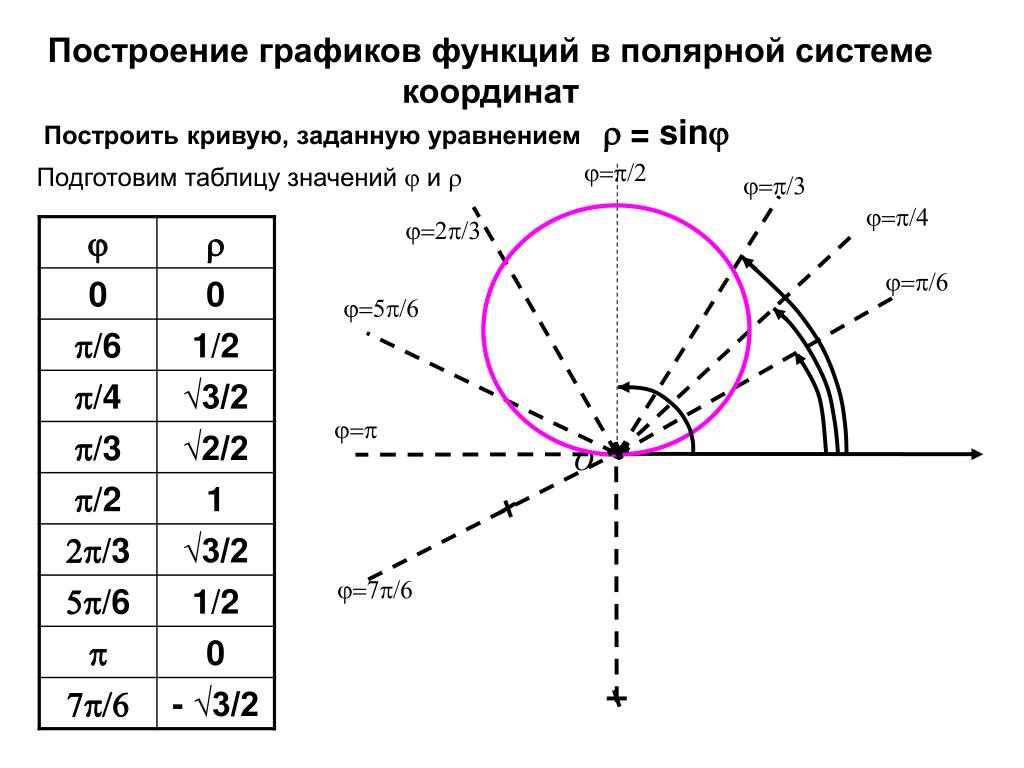 Параметры: количество наблюдений, диапазон наблюдений, статистику для просмотра, идентификаторы данных.
Параметры: количество наблюдений, диапазон наблюдений, статистику для просмотра, идентификаторы данных.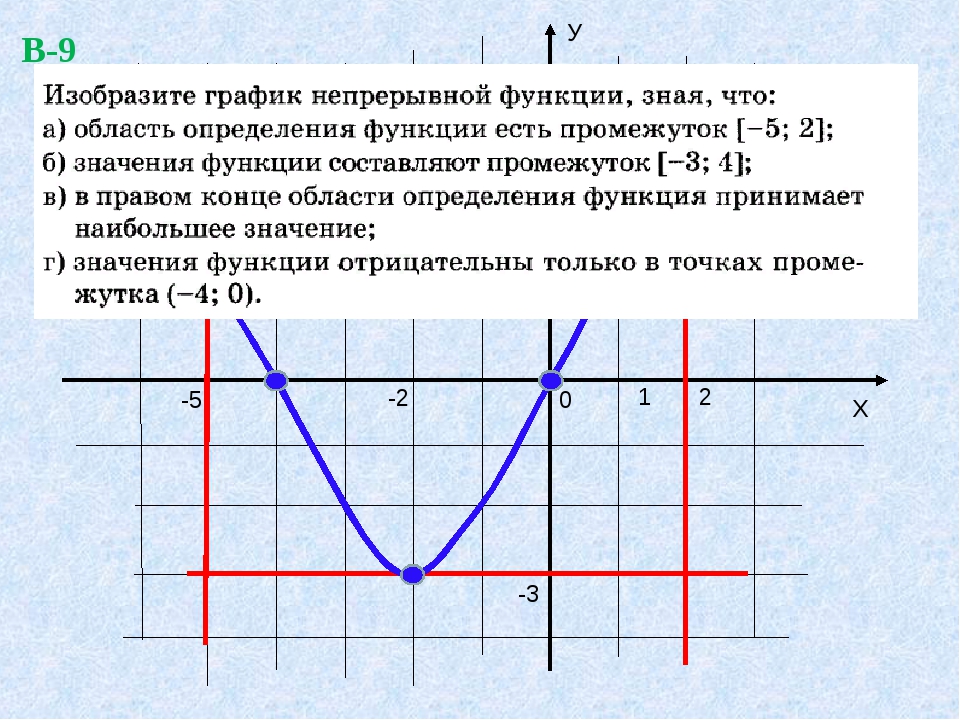 Студенты изучают корреляцию и линии наилучшего соответствия.
Студенты изучают корреляцию и линии наилучшего соответствия.
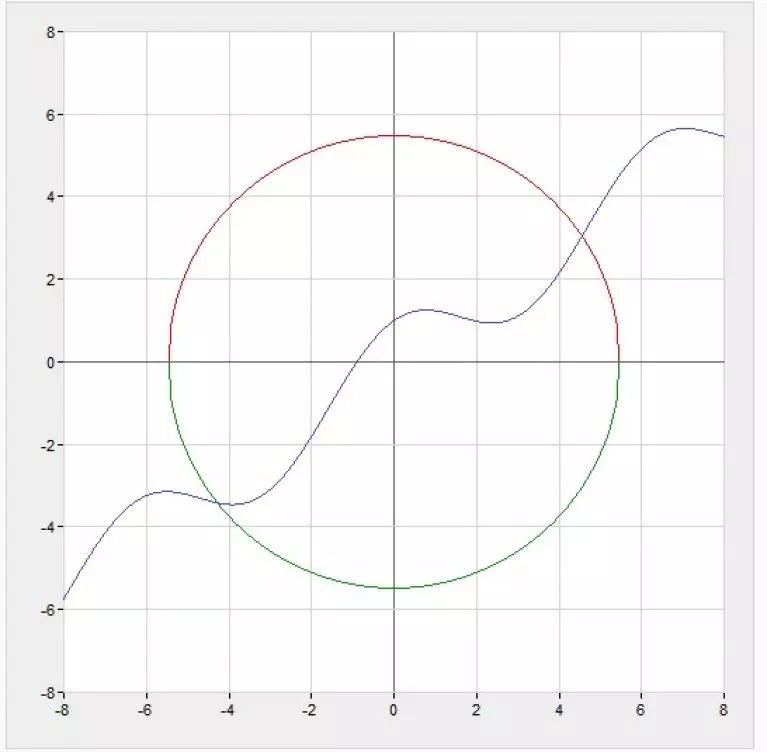 Просмотрите, как изменяются среднее значение, медиана и режим при добавлении записей на график. Параметры: Диапазон для наблюдений.
Просмотрите, как изменяются среднее значение, медиана и режим при добавлении записей на график. Параметры: Диапазон для наблюдений.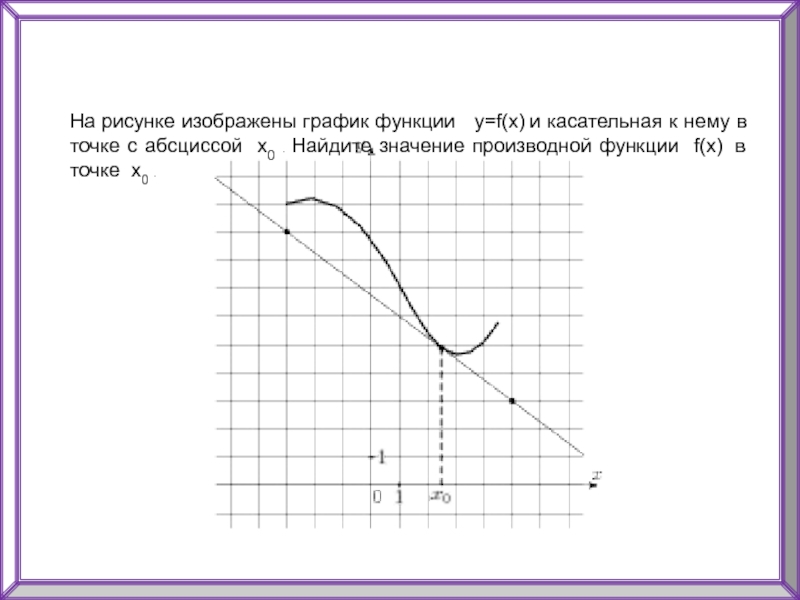 Точки соединяются справа налево, а не в том порядке, в котором они вводятся.
Точки соединяются справа налево, а не в том порядке, в котором они вводятся.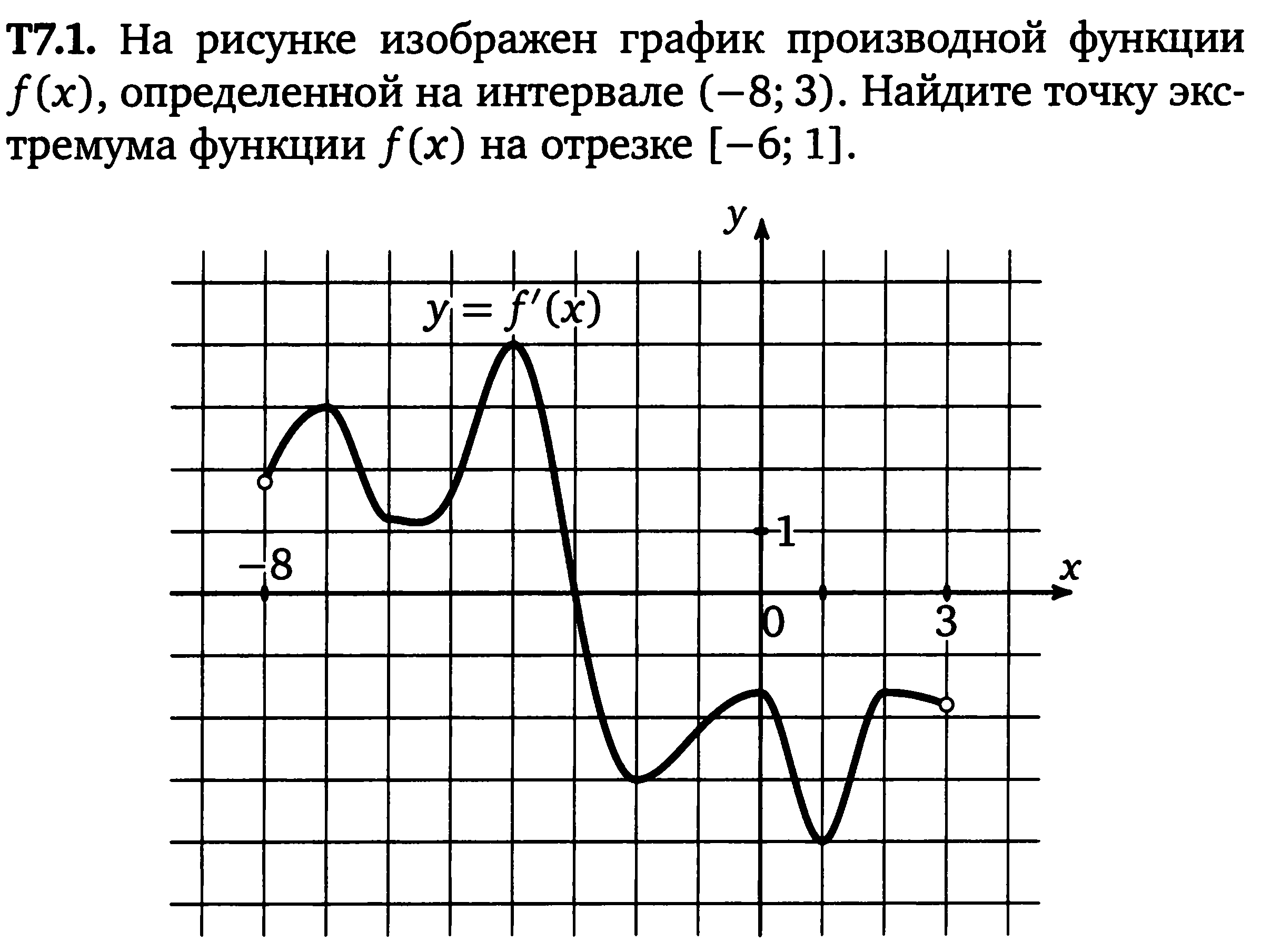

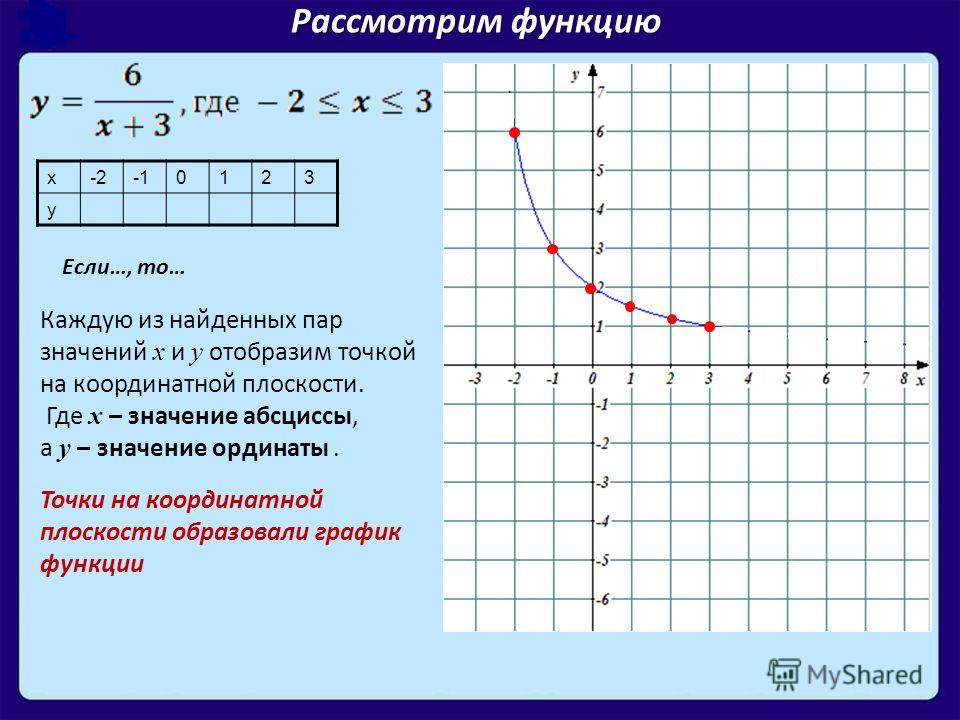
 Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать представление функции в полярной системе координат.
Апплет похож на GraphIt, но вместо этого позволяет пользователям исследовать представление функции в полярной системе координат.
Ваш комментарий будет первым