График функции онлайн калькулятор: Построение графика функции онлайн

Линейная интерполяция Онлайн

Онлайн сервисы >Интерполяция и Экстраполяция онлайн (линейная интерполяция/экстраполяция)

Русский

Polish

Deutsch

x₁

f(x₁)

x_N

f(x_N)

?

x₂

f(x₂)

Уравнение прямой:

Рассчитать

можно использовать:

дроби

1/2, -3/4, 5/7

дробные числа

1.52 или 0,19 можно иcпользовать как «.» так и «,»

квадратный корень

sqrt(4), sqrt(4/3)

тригонометрия

sin(1), cos(1), tan(1), atan(1)

возведение в степень

pow(3, 2) = 3*3 !при pow(3,2, 4,3) — система поймет что вы хотите 3.2 возвести в степень 4.3

арифметические операции

(3/4 + sqrt(5/7)) * pow(2, 4)

Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой.

Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение. Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции

Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₀ и точке x₂, интерполяця помогает найти значение f(x₁) при условии что x₁ принадлежит интервалу от x₀ до x₂. Если x₁ лежит вне интервала (x₀, x₂), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «

линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа

Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₁ и точке x₂, экстраполяция помогает найти значение f(x₀) либо f(x₃) при условии что x₀ либо x₃ меньше либо больше интервала x₁ до x₂. Если x

n лежит в интервале (x₁, x₂), экстраполяция не поможет, для того вам нужно использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.

Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.

Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения

Кредитный калькулятор

Кредитный калькулятор осуществляет 3 типа расчетов:

• Классический – нахождение ежемесячного платежа по заданной сумме и сроку кредита. Такой расчет производят банки при выдаче кредитов.
• Вычисление срока кредита на основе заданной суммы и ежемесячного платежа. Этот вариант интересен тем, что поможет спрогнозировать точный срок возврата кредита при наличии у заемщика конкретных пожеланий к ежемесячному платежу.
• Расчет максимальной суммы кредита по заданному сроку и ежемесячному платежу. Если вы точно знаете, какую сумму и в течение какого времени вы готовы отдавать каждый месяц на погашение кредита, калькулятор сообщит вам, сколько денег вы сможете занять на таких условиях.

Если вам необходим детальный расчет с указанием точных дат, плавающей ставкой и возможностью вносить досрочные платежи, воспользуйтесь расширенным кредитным калькулятором.

Кредитование населения является неотъемлимой частью экономики любой страны. Возможность кредитования повышает спрос на товары и услуги, что является стимулом развития экономики.

Раз вы находитесь на этой странице, значит вы как минимум задумываетесь о получения кредита. Наш калькулятор послужит вам помощником в предварительном расчете.

Кредитный калькулятор — это удобный инструмент для быстрого самостоятельного расчета кредита онлайн.

Калькулятор универсален. Не имеет значения, в каком банке вы будете брать кредит. Не имеет значение и тип займа: потребительский кредит, ипотека, кредит наличными. Результат всегда будет достаточно точным.

На выходе вы получите:

• Размер ежемесячного платежа
• Сумму процентов (переплаты) за весь срок
• Детализированный график погашения по месяцам
• Наглядную диаграмму
• Список подходящих предложений от банков с возможностью оставить заявку онлайн

Что такое процентная ставка и от чего она зависит?

Процентая ставка — самый важный параметр при расчете кредита. Измеряется в процентах годовых. Он показывает сколько процентов начисляется на сумму долга за 1 год. Но фактически проценты начисляются не один раз в год, а ежедневно в размере ставки, разделенной на 365 дней.

У каждого банка есть свои программы кредитования и свои процентные ставки.

Основные факторы, влияющие на процентную ставку:

1. Ключевая ставка Центробанка. Чтобы дать вам кредит, банк занимает у ЦБ по ставке, равной ключевой, накидывает еще несколько процентов сверху и дает вам в долг под более высокий процент, зарабатывая на разнице.

   Выгоднее брать кредит, когда ключевая ставка ниже: вы заплатите меньше процентов. На каждом очередном заседании ЦБ может как повысить, так и понизить ставку или оставить без изменений. Это решение принимается в зависимости от экономической ситуации.

   Вот так ключевая ставка она менялась за последние годы:

   График изменения ключевой ставки с 2013 по 2023 год

2. Тип кредита. Чем больше риска несет кредит для банка, тем он дороже. Например, ипотечный кредит дешевле потребительского кредита или кредита наличными. Причина проста — при выдаче ипотеки банк берет в залог недвижимость, невелируя этим риски невыплаты кредита. При выдаче кредита наличными на любые цели у банка нет способа гарантировать возврат, поэтому ставка гораздо выше.
3. Характиристики заемщика. Среди них кредитная история и отношения с банком. Кредитные организации оценивают надежность потенциальных заемщиков и делают более выгодные персональные предложения потенциальным клиентам, в надежности которых они уверены. Своим зарплатным клиентам многие банки предоставляют скидку в размере 0.3 — 0.6 процентных пункта.

Аннуитетный и дифференцированный платеж

Что такое аннуитетный и дифференцированный платеж? В чем разница между ними? Какой из них выгоднее для заемщика?

Аннуитетный

Представляет собой равные ежемесячные суммы на протяжении всего срока кредитования.

Доля процентов и доля основного долга в каждом месяце рассчитываются таким образом, чтобы общая сумма была неизменной.

---

Аннуитетный платеж более распространен за счет удобства выплаты. Платить каждый месяц одну и ту же сумму логичнее и проще для учета финансов.

---

Переплата по кредиту выше, чем при дифференцированном платеже.

Дифференцированный

Сумма ежемесячного платежа уменьшается к концу срока кредитования.

Доля основного долга остается неизменной, а доля процентов с каждым месяцем уменьшается, так как уменьшается общая сумма долга.

---

Ежемесячные платежи вначале срока выше по сравнению с аннуитетом, поэтому выше требования к платежеспоособности клиента.

---

При прочих равных дифференцированный платеж выгоднее, сумма переплаты ниже.

Графический калькулятор — MathCracker.com

Инструкции: Используйте этот калькулятор графиков, чтобы построить график любой функции, которую вы предоставляете. Введите допустимую функцию, которую вы хотите построить, в поле формы ниже.

Подробнее об этом графическом калькуляторе 92, или вы также можете указать что-то более сложное, например f(x) = tan(x)/x. Этот калькулятор попытается упростите выражение перед построением его графика.

После того, как действительная функция будет предоставлена, все, что вам нужно сделать, это нажать кнопку «График», и вам будет предоставлен график онлайн, а также любые соответствующие упрощения, если есть. 2(x) = 1\), а затем упростить это в вашем выражении.

Шаг 2: После того, как все очевидные упрощения сделаны, вам нужно выбрать диапазон для значений x. Для этого нет фиксированных правил, но обычно вам необходимо учитывать все важные моменты, такие как разрывы, вертикальные асимптоты и т. д.

Шаг 3: После того, как диапазон значений x определен, вам нужно получить представление о диапазоне значений y, чтобы ни одна точка графика не выпадала из кадра.

Итак, идея построения графика проста, но вам все равно нужно решить несколько вещей, если вы будете делать что-то вручную. Использование графического инструмента определенно удалить любые догадки.

Зачем мне нужен график функции

График, предоставленный этим графическим онлайн-калькулятором, гарантирует, что вы получите действительно хорошее изображение поведения функции. Пересекает ли он x или y ось, имеет ли она локальные точки максимума или минимума? Вы можете получить много важной информации о функции, просто взглянув на график.

Вы не обязательно будете знать точные точки пересечения или экстремумы, просто взглянув на график, но у вас будет довольно хорошее представление о том, где их найти, если они даже есть.

Преимущества использования инструмента для построения графиков

Как мы уже говорили, построить график не так уж сложно, но есть детали, которые необходимо упорядочить, особенно те, которые определяют рамка окна, которая будет отображаться.

Это означает, что у вас может быть «правильный» график для функции, но он отображает часть графика, которая не является наиболее значимой, и вы может отсутствовать большинство важных частей функции, которые было бы неплохо отобразить. Хороший производитель графиков сделает это за вас.

Пример: Расчет графика функции

Найдите график функции: \(f(x) = \displaystyle \frac{\sin x}{x}\)

Решение: Следующая функция имеет предоставлено: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), для чего мы необходимо построить его график.

Обратите внимание, что функция не определена в \(x = 0\), хотя она имеет поправимый разрыв, поскольку

\[\lim_{x\to 0} \frac{\sin x}{x} = 1\]

Для заданной функции на интервале \([-5, 5]\) получается следующий график:

, который завершает расчет.

Другие онлайн-калькуляторы с графиками

Хотя этот конструктор графиков является универсальным в том смысле, что он может отображать функции любого типа, вы также можете использовать специальные типы графиков для определенных функций, который может дать вам больше информации на основе структуры функции.

Например, вы можете использовать калькулятор линейных графиков, специально разработанный для построения графиков. Или, если вы имеете дело с триггерной функцией, вы можете использовать этот триггерный калькулятор, который также попытается найти конкретные параметры триггерных функций, включая амплитуду, период, частота и т. д.

Или вы можете использовать этот полиномиальный график при работе с полиномами.

Кроме того, вы можете использовать этот калькулятор экспоненциальной функции, чтобы найти параметры экспоненциальной функции Даны две точки, через которые проходит кривая.

Взлет — и возможное падение — графического калькулятора — Digital Promise

Эта статья перепечатана из The Conversation под лицензией Creative Commons. Прочитайте оригинальную статью.

Первый портативный графический калькулятор, Casio fx-7000G, появился в 1985 году.

С тех пор графические калькуляторы стали распространенным и противоречивым инструментом для изучения математики. Эти устройства могут выполнять все расчеты научного калькулятора, а также графические уравнения, составлять таблицы функций и решать уравнения. Многие умеют проводить статистический анализ и даже некоторые расчеты.

Защитники утверждают, что калькуляторы предоставляют учащимся доступ к более мощной математике. Критики опасаются, что они могут повредить беглости учащихся в базовой математике и стандартных алгоритмах.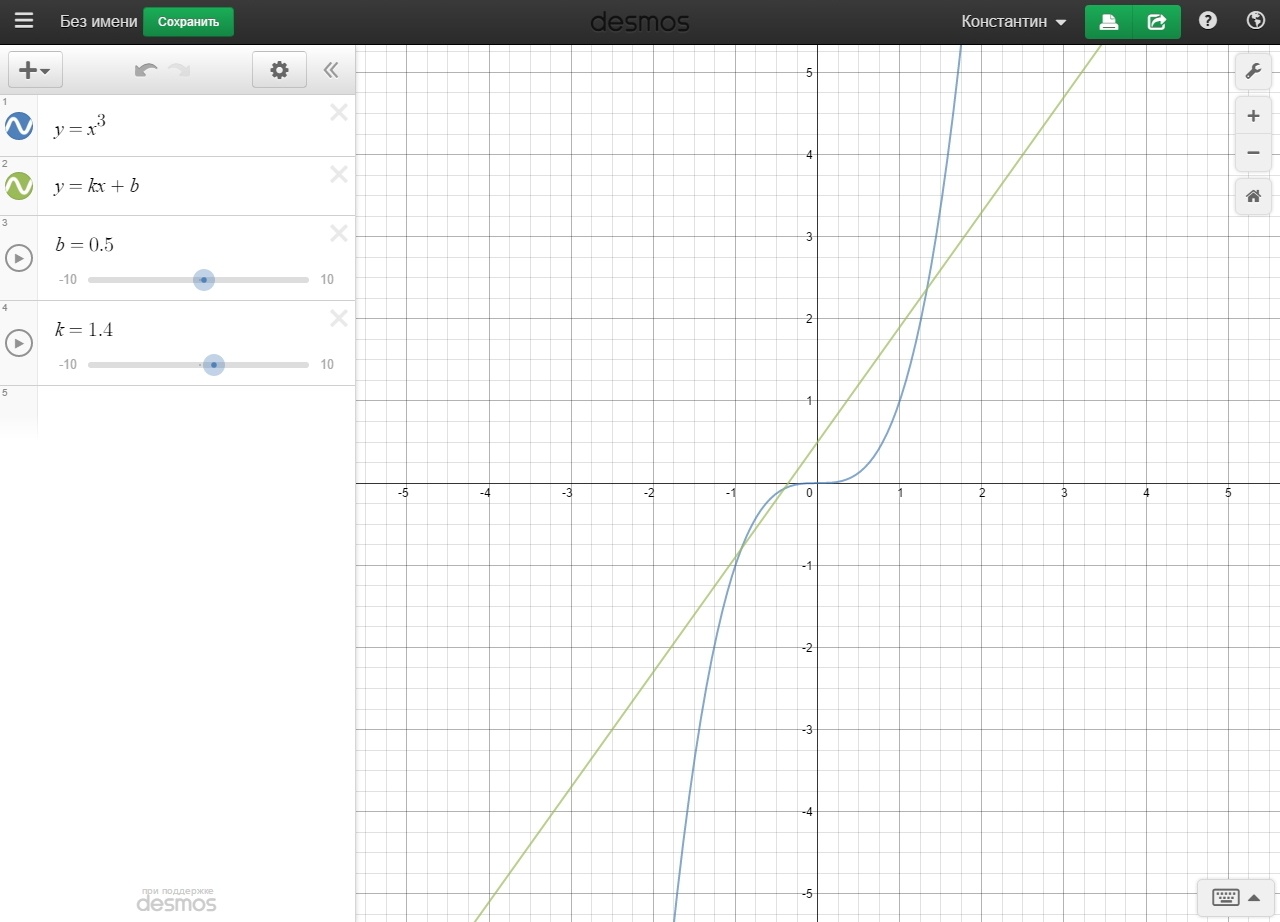

Сегодня некоторые учителя заменяют дорогие графические калькуляторы бесплатными приложениями, которые могут больше. Но даже после десятилетий использования графическая технология любого рода в классе по-прежнему вызывает споры.

Как преподаватели математики, мы считаем, что графический калькулятор изменил американские классы к лучшему. Будут ли учителя продолжать использовать эти инструменты или откажутся от них в пользу новых, графические технологии, вероятно, всегда будут иметь место в среднем математическом образовании.

Понимание математики

Преподаватели математики часто говорят о двух видах понимания.

«Инструментальное понимание» происходит от освоения процедуры или запоминания факта без реального понимания математики, стоящей за этим. Это знание как, но не почему. Поговорка «Не наше дело гадать, почему, просто переверни и умножь!» — который иногда используется для обучения делению дробей — передает такое понимание.

Напротив, «реляционное понимание» — это своего рода связанное, концептуальное понимание. Люди с реляционным пониманием не просто знают, как инвертировать и умножать, они знают, почему такая процедура приводит к частному двух дробей.

Сторонники графических калькуляторов в школах увидели перспективу в способности этого инструмента помочь учащимся развить понимание отношений. В то время как калькулятор заботится о том, «как», студенты могут сосредоточиться на том, «почему».

Воздействие совершенно очевидно в программе исчисления Advanced Placement (AP), которая начала требовать графических калькуляторов в своих курсах и на экзаменах в 1995 году. использовать правила для нахождения производных и интегралов функций. После 1995, произошел заметный сдвиг от этого инструментального понимания к вопросам, которые исследовали реляционное понимание.

По мере развития экзаменов развивалось и преподавание философии. Программа AP требовала, чтобы учителя использовали графические калькуляторы на своих курсах. Это было сделано не только для того, чтобы студенты научились пользоваться калькулятором. Скорее, фокус обучения сместился, чтобы учащиеся могли изучать математику с помощью графического калькулятора.

Например, используя графические функции и функции масштабирования графического калькулятора, учащиеся могут сравнить и сопоставить локальное и глобальное поведение таких функций, как y = x ² и y = x ² + 2. При увеличении масштаба учащиеся видят, что в любой локальной области графики явно отличаются. Уменьшив масштаб, учащиеся могут увидеть, что в целом графики в основном идентичны. Благодаря таким исследованиям учащиеся получили относительное понимание бесконечных пределов.

Технология помогает или вредит?

Тем не менее, некоторые учителя задавались вопросом, не окажет ли этот сдвиг в обучении математике AP и в учебной программе K-12 негативное влияние на инструментальное понимание учащихся. В конце концов, если за вас вычисляет машина, зачем ей учиться?

После более чем трех десятилетий исследований выводы ясны. Графические калькуляторы оказывают положительное влияние на понимание учащимися отношений и небольшое положительное влияние на их инструментальное понимание.

Другой обзор, проведенный уважаемыми исследователями в области математического образования (но финансируемый компанией-калькулятором), пришел к аналогичному выводу.

Другими словами, учащиеся, которые используют графические калькуляторы в школе, знают как минимум столько же основных фактов и как минимум так же хорошо справляются со стандартными алгоритмами, как и учащиеся, которые не используют графические калькуляторы. Однако учащиеся, использующие графические калькуляторы, лучше понимают «почему» эти алгоритмы.

Конечно, есть много отдельных исследований, которые показывают незначительное или даже негативное влияние графических калькуляторов. Но в целом, когда технология сочетается с соответствующими методами обучения, результатом становится больше и лучше изучение математики.

Рост графических приложений

Сегодня онлайн-технологии и технологии на основе приложений, такие как Desmos и GeoGebra, стремятся заменить роль автономных графических калькуляторов в школе.

Как и в случае с графическими калькуляторами, для того чтобы эти новые технологии оказали положительное влияние на обучение учащихся, учителя должны адаптировать свои инструкции, изменив то, что они преподают, и то, как они преподают.

Например, технология может помочь учащимся связать графические представления с алгебраическими уравнениями. Недавно мы наблюдали, как ученики седьмого класса в Миссуле, штат Монтана, делали это с помощью Desmos. Студенты построили три разных линейных уравнения, каждое с разными коэффициентами для члена x . На основе этого исследования учащиеся делали предположения о роли коэффициента и использовали приложение для проверки своих предположений — например, с помощью «ползунка» для динамического изменения коэффициента. Гибкость технологии также побуждала студентов задавать и исследовать свои собственные вопросы.

Даже несмотря на то, что эти облачные и прикладные инструменты предоставляют мощные технологии бесплатно для смартфонов и других персональных устройств, дорогой графический калькулятор (который обычно стоит от 80 до 150 долларов США) продолжает оставаться верным помощником в математических классах K-12, при этом в 2015 и 2016 годах объем продаж по сравнению с прошлым годом увеличился.