2+n-72)=1/(n+9)Решение высшей математики онлайн
‹— Назад
Определение 12.3 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Для эллипса можно дать еще несколько эквивалентных определений. Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс — это кривая, получающаяся как проекция на плоскость окружности, лежащей в плоскости, которая образует острый угол с плоскостью .
В отличие от окружности, записать в «удобном» виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.
Пусть и — фокусы эллипса.
Начало системы координат расположим на середине отрезка . Ось направим вдоль этого отрезка, ось — перпендикулярно к этому отрезку (рис. 12.3).
Теорема 12.2 Пусть сумма расстояний от точки эллипса до фокусов равна , а расстояние между фокусами — . Тогда в выбранной системе координат эллипс имеет уравнение
| (12.4) |
где
| (12.5) |
Доказательство. Пусть — текущая точка эллипса. По определению эллипса . Из треугольника (рис. 12.3) видно, что , то есть , , и поэтому число существует.
Рис.12.3.
Фокусами в выбранной системе координат являются точки , . По формуле (10.4) для плоского случая находим
Тогда по определению эллипса
Пренесем один из корней вправо и обе части возведем в квадрат:
После того, как раскроем скобки и приведем подобные члены, приходим к выражению
Разделим обе части этого уравнения на 4 и возведем в квадрат
Раскроем скобку и приведем подобные члены
Учитывая, что , имеем равенство
Наконец, разделив обе части на , получим уравнение (12.4).
Уравнение (12.4) называется каноническим уравнением эллипса.
Прежде, чем нарисовать эллипс, выясним некоторые его свойства.
Предложение 12.
1 Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением (12.4), то его осями симметрии служат оси и , начало координат — центр симметрии.
Доказательство. Можно было бы провести доказательство на основе определения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического аспекта мы проведем доказательство на основе уравнения (12.4).
Пусть эллипс задан уравнением (12.4) и — какая-то точка эллипса. Тогда
| (12.6) |
Точка является точкой, симметричной точке относительно оси (рис. 12.4).
Рис.
12.4.Симметрия точек
Вычисляем значение левой части уравнения (12.4) в точке
В силу равенства (12.6) получаем
следовательно, точка лежит на эллипсе. Точка является точкой симметричной точке относительно оси (рис. 12.4). Для нее аналогичным путем убеждаемся, что
то есть является точкой эллипса. Наконец точка является симметричной точке относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.
Проведем построение эллипса, заданного уравнением (12.4). Заметим, что из-за симметрии достаточно нарисовать часть эллипса, лежащую в верхней полуплоскости. Уравнение этой линии мы получим, выразив из уравнения (12.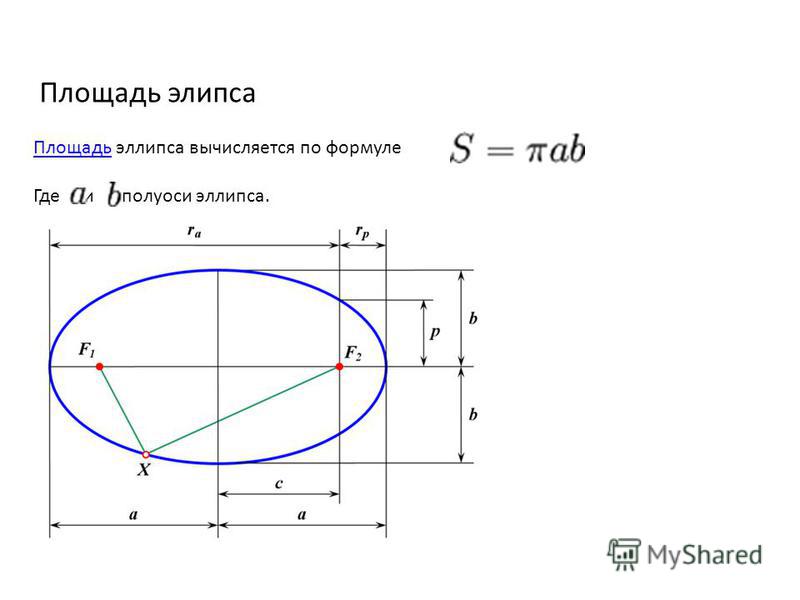
4) и взяв перед корнем знак » «,
Построим график этой функции. Область определения — отрезок , , при увеличении переменного от 0 до функция монотонно убывает. В силу симметрии графика относительно оси функция монотонно растет при изменении от до 0. Производная определена во всех точках интервала и, следовательно, график является гладким (не содержит изломов, касательная есть в любой точке). Вторая производная отрицательна во всех точках интервала , следовательно, график — выпуклый вверх.
Осталось не исследованным поведение кривой вблизи концов отрезка . Выразим из уравнения (12.4) переменное через : . Очевидно, что в точке эта функция имеет производную, то есть касательная к этому графику в точке существует. Легко проверить, что она параллельна оси . Из симметрии эллипса делаем вывод, что это гладкая кривая и строим ее с учетом полученных данных (рис.
12.5).
Рис.12.5.Эллипс
Определение 12.4 Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии — центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины — большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины — малой полуосью. Величина называется эксцентриситетом эллипса.
Если эллипс задан каноническими уравнениями, то его вершины имеют координаты , , , , большая полуось равна , малая полуось равна . Величина , являющаяся половиной расстояния между фокусами, определяется из формулы (12.5) для величины , а именно, .
Замечание 12.1 Уравнение (12.4) было получено в предположении, что и — различные точки, то есть .
Тогда . Но кривую, определяемую уравнением (12.4), мы можем рассмотреть и в случае , . Уравнение (12.4) в этом случае после умножения на примет вид . Это — уравнение окружности радиуса с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда , , или, как иногда говорят математики, окружность является «вырожденным» эллипсом, у которого фокусы совпали.
Эксцентриситет эллипса характеризует степень вытянутости эллипса. Чем ближе экцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса .
Если задано каноническое уравнение эллипса и требуется его построить, то для отображения качественных характеристик достаточно правильно отметить вершины эллипса и провести через них линию, похожую на кривую рис. 12.4, выдерживая симметрию и избегая образования углов на рисунке.
Если же из рисунка предполагается получать числовую информацию о координатах его точек, то тогда построение следует проводить более точно. Нужно построить по точкам верхнюю половину эллипса как график функции , взяв для построения достаточно много точек, а нижнюю половину эллипса получить, используя его симметрию. С другим способом построения эллипса можно познакомиться в курсе черчения.
Эллипс обладает многими замечательными свойствами. Приведем без доказательства одно из них (рис. 12.6).
Предложение 12.2 Пусть и — фокусы эллипса, — произвольная точка на эллипсе. Тогда нормаль (перпендукуляр к касательной) к эллипсу в точке делит угол пополам.
Рис.12.6.Отражение лучей света от эллипса
Данное свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то отразившись от самого эллипса, он обязательно пройдет через другой фокус.
Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, то есть освещенность в обоих фокусах будет одинаковой.
Пример 12.2 Постройте кривую . Найдите фокусы и эксцентриситет.
Решение. Разделим обе части уравнения на 36. Получаем уравнение
Это — каноническое уравнение эллипса, , . Делаем чертеж (рис. 12.7)
Рис.12.7.Эллипс, заданный уравнением
Из соотношения (12.5) находим , . Фокусы — , , эксцентриситет —
Пример 12.3 Нарисуйте эллипс .
Найдите его фокусы и эксцентриситет.
Решение. Уравнение запишем в виде
| (12.7) |
Это уравнение не является каноническим уравнением эллипса, так как в соответствии с уравнением (12.4) в нем , , , а должно быть . Однако, если переобозначить оси, то есть положить , , то уравнение (12.7) в координатах примет вид
Это — каноническое уравнение эллипса при , . Делаем чертеж (рис. 12.8).
Рис.12.8.Эллипс, заданный уравнением
Из соотношения (12.5) находим . Значит, фокусы в системе координат имеют координаты , , а в системе координат — координаты , .
Эксцентриситет равен .
Замечание 12.2 Из примера 12.3 ясно, что построение кривой (эллипса) с уравнением (12.4) при можно вести так же, как и для эллипса, заданного каноническим уравнением: отложить полуось на оси , полуось — на оси и через получившиеся вершины провести эллипс. Различие заключается в том, что фокусы теперь располагаются на оси ординат (большой оси), величину нужно вычислять по формуле , и .
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Создайте свою собственную плоскость эллипса
Вы можете настроить свою плоскость с помощью этого онлайн-инструмента *.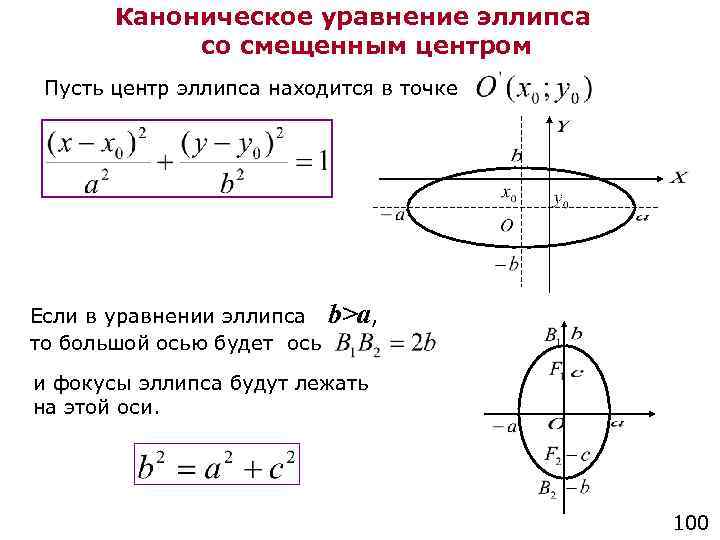
Нажмите , чтобы начать новую конфигурацию , чтобы насладиться настройкой вашего нового самолета с нуля, шаг за шагом. В качестве альтернативы, выберите из нашего трио предварительно сконфигурированных самолетов.
* Визуализация самолета в конфигураторе носит иллюстративный характер и не отражает реальную конструкцию самолета
Запустить новую конфигурацию
Предварительно настроенный самолет в соответствии с нашими рекомендациями:
SPORT
Лучший выбор для тех, кто любит пилотировать на высокой скорости и ищет максимум удовольствия.
ПУТЕШЕСТВИЯ
Полностью оборудованный самолет для дальних и безопасных путешествий не только для приключений по всему миру.
CLUB
Идеальный выбор для аэроклубов, летной подготовки и обмена между пилотами.
Вернуться к итогуЦена спроса
Вас интересует цена вашего аэроплана ellipse? Не стесняйтесь обращаться к нам!
Спасибо за ваш запрос о плоскости эллипса.
Мы свяжемся с вами в ближайшее время по указанным контактам.Name and surname
Phone
Select a countryArubaAfghanistanAngolaAnguillaÅland IslandsAlbaniaAndorraUnited Arab EmiratesArgentinaArmeniaAmerican SamoaAntarcticaFrench Southern TerritoriesAntigua and BarbudaAustraliaAustriaAzerbaijanBurundiBelgiumBeninBonaire, Sint Eustatius and SabaBurkina FasoBangladeshBulgariaBahrainBahamasBosnia and HerzegovinaSaint BarthélemyBelarusBelizeBermudaBolivia (Plurinational State of)BrazilBarbadosBrunei DarussalamBhutanBouvet IslandBotswanaCentral African RepublicCanadaCocos (Keeling) IslandsSwitzerlandChileChinaCôte д’ИвуарКамерунКонго, Демократическая Республика КонгоОстрова КукаКолумбияКоморские островаКабо-ВердеКоста-РикаКубаКюрасаоОстров РождестваКаймановы островаКипрЧехияГерманияДжибутиДоминикаДанияДоминиканская РеспубликаАлжирЭквадорЕгипетЭритреяЗападная СахараИспанияЭстонияЭфиопияФинляндияФиджиФолклендские острова (Великобритания)Габонские островаФедер (Мальвинские острова)ФранцияФареры tain and Northern IrelandGeorgiaGuernseyGhanaGibraltarGuineaGuadeloupeGambiaGuinea-BissauEquatorial GuineaGreeceGrenadaGreenlandGuatemalaFrench GuianaGuamGuyanaHong KongHeard Island and McDonald IslandsHondurasCroatiaHaitiHungaryIndonesiaIsle of ManIndiaBritish Indian Ocean TerritoryIrelandIran (Islamic Republic of)IraqIcelandIsraelItalyJamaicaJerseyJordanJapanKazakhstanKenyaKyrgyzstanCambodiaKiribatiSaint Kitts and NevisKorea, Republic ofKuwaitLao People’s Democratic RepublicLebanonLiberiaLibyaSaint LuciaLiechtensteinSri LankaLesothoLithuaniaLuxembourgLatviaMacaoSaint Martin (French part)MoroccoMonacoMoldova, Republic ofMadagascarMaldivesMexicoMarshall IslandsNorth MacedoniaMaliMaltaMyanmarMontenegroMongoliaNorthern Mariana IslandsMozambiqueMauritaniaMontserratMartiniqueMauritiusMalawiMalaysiaMayotteNamibiaNew CaledoniaNigerNorfolk IslandNigeriaNicaraguaNiueNetherlandsNorwayNepalNauruNew ЗеландияОманПакистанПанамаПиткэрнПеруФилиппиныПалауПапуа-Новая ГвинеяПольшаПуэрто-РикоКорея (Демократическая ratic People’s Republic of)PortugalParaguayPalestine, State ofFrench PolynesiaQatarRéunionRomaniaRussian FederationRwandaSaudi ArabiaSudanSenegalSingaporeSouth Georgia and the South Sandwich IslandsSaint Helena, Ascension and Tristan da CunhaSvalbard and Jan MayenSolomon IslandsSierra LeoneEl SalvadorSan MarinoSomaliaSaint Pierre and MiquelonSerbiaSouth SudanSao Tome and PrincipeSurinameSlovakiaSloveniaSwedenEswatiniSint Maarten (Dutch part)SeychellesSyrian Arab RepublicTurks and Caicos IslandsChadTogoThailandTajikistanTokelauTurkmenistanTimor -LesteТонгаТринидад и ТобагоТунисТурцияТувалуТайвань, провинция КитаяТанзания, Объединенная Республика УгандаУкраинаОтдаленные малые острова СШАУругвайСоединенные Штаты АмерикиУзбекистанСвятой ПрестолСент-Винсент и ГренадиныВенесуэла (Боливарианская Республика)Виргинские острова (Британия)Виргинские острова (США)ВьетнамЮжная АфрикаЗамбиВануатуУоллис и Фут0005
Ваша конфигурация
Текст вашего сообщения
Даю согласие на обработку персональных данных на основании политики конфиденциальности.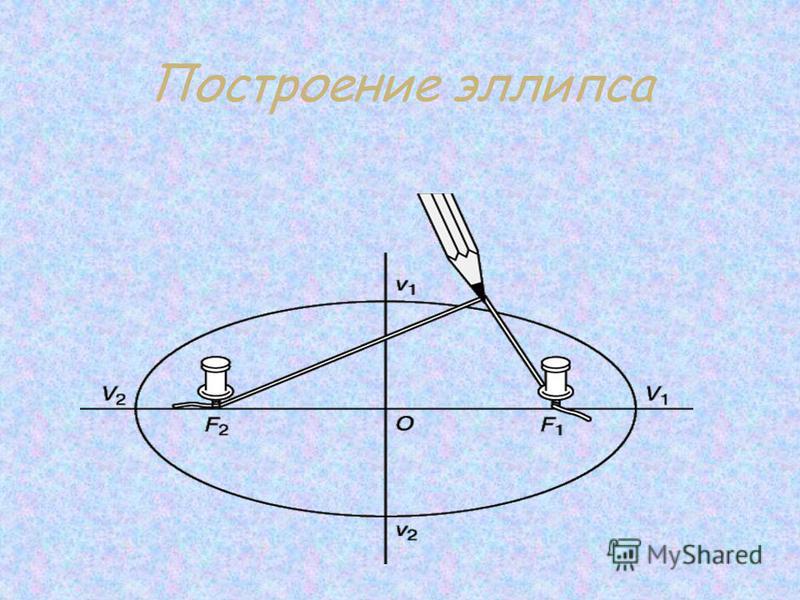
Выбранный вариант конфликтует с предыдущим выбором.
Вы хотите удалить ?
Скопируйте этот URL-адрес, чтобы вернуться к своей конфигурации позже.
Калькулятор эллипса — eMathHelp
Этот калькулятор найдет либо уравнение эллипса по заданным параметрам, либо центр, фокусы, вершины (большие вершины), ко-вершины (второстепенные вершины), (полу)длину большой оси, ( длина полу)малой оси, площадь, окружность, латеральная прямая, длина латеральной прямой, фокальный параметр, фокусное расстояние (расстояние), эксцентриситет, линейный эксцентриситет, директрисы, точки пересечения по оси X, точки пересечения по оси Y, домен и диапазон введенных значений эллипс. Кроме того, он будет отображать эллипс. Шаги доступны.
Связанные калькуляторы: Калькулятор параболы, Калькулятор окружности, Калькулятор гиперболы, Калькулятор конического сечения
Тип:
из уравненияиз данных
Уравнение:
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
9{2}} = \sqrt{5}$$$.
Эксцентриситет равен $$$e = \frac{c}{a} = \frac{\sqrt{5}}{3}$$$.
Первый фокус $$$\left(h — c, k\right) = \left(- \sqrt{5}, 0\right)$$$.
Второй фокус $$$\left(h + c, k\right) = \left(\sqrt{5}, 0\right)$$$.
Первая вершина $$$\left(h — a, k\right) = \left(-3, 0\right)$$$.
Вторая вершина $$$\left(h + a, k\right) = \left(3, 0\right)$$$.
Первая ковершина $$$\left(h, k — b\right) = \left(0, -2\right)$$$. 9{2}}{c} = \frac{9 \sqrt{5}}{5}$$$.
Х-пересечения можно найти, установив $$$y = 0$$$ в уравнении и решив $$$x$$$ (шаги см. в калькуляторе перехватов).
x-отрезки: $$$\left(-3, 0\right)$$$, $$$\left(3, 0\right)$$$
y-отрезки можно найти, установив $ $$x = 0$$$ в уравнении и решение для $$$y$$$: (шаги см. в калькуляторе перехватов).
y-отрезки: $$$\left(0, -2\right)$$$, $$$\left(0, 2\right)$$$
Домен $$$\left[h — а, ч + а\вправо] = \влево[-3, 3\вправо]$$$. 9{2}}{9}$$$А.
График: см.
графический калькулятор.
Центр: $$$\влево(0, 0\вправо)$$$A.
Первый фокус: $$$\влево(-\sqrt{5}, 0\вправо)\приблизительно \влево(-2,23606797749979, 0\вправо)$$$A.
Второй фокус: $$$\left(\sqrt{5}, 0\right)\приблизительно \left(2.23606797749979, 0\right)$$$A.
Первая вершина: $$$\left(-3, 0\right)$$$A.
Вторая вершина: $$$\left(3, 0\right)$$$A.
Первая ковершина: $$$\left(0, -2\right)$$$A.
Вторая ковершина: $$$\left(0, 2\right)$$$A.
Длина главной оси: $$$6$$$A.
Длина большой полуоси: $$$3$$$A.
Длина малой оси: $$$4$$$A.
Длина малой полуоси: $$$2$$$A.
Площадь: $$$6 \pi\ок. 18,849555921538759$$$A.
Окружность: $$$12 E\left(\frac{5}{9}\справа)\приблизительно 15,86543958929059$$$A.
Первая широкая прямая кишка: $$$x = — \sqrt{5}\приблизительно -2,23606797749979$$$A.
Вторая широкая прямая кишка: $$$x = \sqrt{5}\приблизительно 2,23606797749979$$$A.
Концы первой широкой прямой кишки: $$$\left(- \sqrt{5}, — \frac{4}{3}\right)\приблизительно \left(-2.23606797749979, -1.3333333333333333\right)$ $$, $$$\left(-\sqrt{5}, \frac{4}{3}\right)\приблизительно \left(-2,23606797749979, 1,333333333333333\right)$$$A.
Концы второй широкой прямой кишки: $$$\left(\sqrt{5}, — \frac{4}{3}\right)\приблизительно \left(2.23606797749979, -1.333333333333333\right)$$$, $$$\left(\sqrt{5}, \frac{4}{3}\right)\приблизительно \left(2.23606797749979, 1.3333333333333333\right)$$$A.
Длина латерального отдела прямой кишки: $$$\frac{8}{3}\примерно 2,666666666666667$$$A.
Параметр фокуса: $$$\frac{4 \sqrt{5}}{5}\приблизительно 1,788854381999832$$$A.
Ваш комментарий будет первым