| 1 | Оценить с использованием заданного значения | квадратный корень 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | y=x+4 | ||
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень 1 | |
| 69 | Упростить | квадратный корень 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
1.
 4.7. Трехмерные графики MathCAD 12 руководство
4.7. Трехмерные графики MathCAD 12 руководствоКоллекция трехмерных графиков — настоящее чудо, которое Mathcad дарит пользователю. За считанные секунды вы можете создать великолепную презентацию результатов своих расчетов. Рамки данной книги не позволяют описать технику их создания и форматирования подробно, поэтому мы ограничимся лишь вводными замечаниями и простыми примерами, которые помогут ориентироваться в дальнейшем материале. Для этого рассмотрим на простом примере функции z(x,y) и матрицы z (они заданы в листингах 1.22 и 1.23 соответственно) технику построения трехмерных графиков различных типов
Чтобы создать трехмерный график, требуется нажать кнопку с изображением любого из типов трехмерных графиков на панели инструментов
Graph (График). В результате появится пустая область графика с тремя осями (рис. 1.34) и единственным местозаполнителем в нижнем левом углу. В этот местозаполнитель следует ввести либо имя
z функции z(x,y) двух переменных для быстрого построения трехмерного графика (рис. 1.35), либо имя матричной переменной
z, которая задаст распределение данных zx,Y на плоскости XY (рис. 1.36). Еще раз отметим, что для получения графиков (и этих, и последующих) не требуется никакого текста, кроме соответствующего листинга и введения имени соответствующей функции или матрицы в местозаполнитель.
1.35), либо имя матричной переменной
z, которая задаст распределение данных zx,Y на плоскости XY (рис. 1.36). Еще раз отметим, что для получения графиков (и этих, и последующих) не требуется никакого текста, кроме соответствующего листинга и введения имени соответствующей функции или матрицы в местозаполнитель.
Рис. 1.34. Создание трехмерного графика
Листинг 1.22. Функция для быстрого построения трехмерных
графиков
Листинг 1.23. Матрица для отображения на трехмерных графиках
Помимо трехмерных графиков поверхности, нажатие соответствующих кнопок на панели
Graph (График) приводит к созданию графика линий уровня (рис. 1.37), трехмерной гистограммы (рис. 1.38), трехмерного распределения точек (рис. 1.39) или векторного поля (рис. 1.40). Все эти графики представляют данные, составленные листингами 1.22 и 1.23.
Рис. 1.35. Быстрое построение графика поверхности функции (продолжение листинга 1.22)
Рис. 1.36. График поверхности, заданный матрицей (продолжение листинга 1. 23)
23)
Форматирование трехмерных графиков выполняется с помощью диалогового окна 3-D Plot Format
(Форматирование 3-D графика), которое вызывается двойным щелчком мыши.
Рис. 1.37. Быстрое построение графика линий уровня (продолжение листинга 1.22)
Рис. 1.38. Быстрое построение трехмерной гистограммы (продолжение листинга 1.22)
Рис. 1.39. Быстрое построение графика трехмерного распределения точек (продолжение листинга 1.22)
Рис. 1.40. Два графика векторных полей, заданных матрицами (продолжение листинга 1.23)
Сюжеты MathCad
Комментарии ()
Вы должны авторизоваться, чтобы оставлять комментарии.
Радиомастер
© 2005–2017 radiomaster.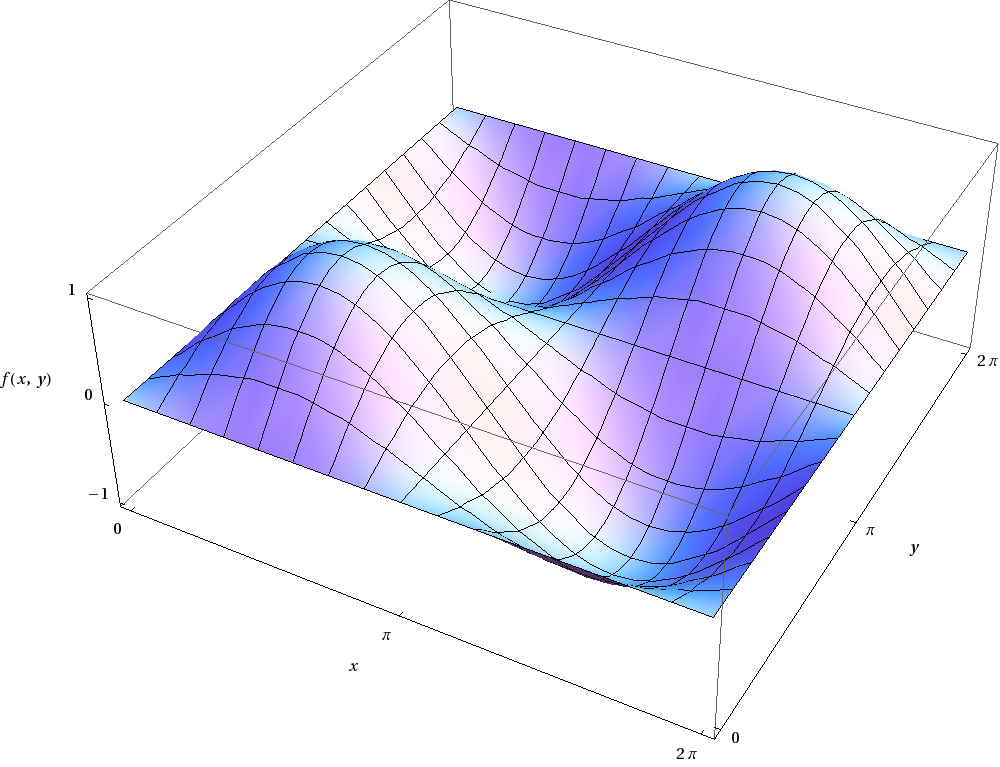 ru
ru
| Главная > Учебные материалы > Математика: Функции нескольких переменных | ||||
|
1.Основные пониятия.
|
||||
| 11 12 13 14 15 16 17 18 19 | ||||
1. Основные понятия. Основные понятия.
Многие явления и процессы в экономике, физике и других областях науки сложно изучить и объяснить с помощью функции от одной переменной. Поэтому в математике введен раздел и понятие функции нескольких переменных. Например, площадь боковой поверхности конуса можно выразить в виде функции от двух переменных S = π R l. где |
||||
|
Т.е. площадь есть функция от двух переменных S (R,l). Путь, пройденный за определенный промежуток времени с определенной скоростью, также можно выразить в виде функции от двух переменных S = vt т.е. S (v,t). где |
||||
|
Исходя из этого можно дать такое определение: однозначное соответствие n независимых переменных величин (x1,x2,x3,. Х — называется областью определения функции, y — область значений функции. Если n = 2, то независимых переменных две и областью определения Х есть подмножество точек на координатной плоскости Оxy. Графиком функции от двух переменных называется совокупность точек в трехмерной системе координат с осями ОХ ОY и OZ. |
||||
Пример 1Построить график функции z (x,y) = (5x)² + y². Как видно из графика, в сечении поверхности z (x,y) = (5x)² + y² плоскостями Оzx, Ozy будут параболы. Например, если присвоить переменной x или y какое-либо фиксированное значение, то получим уравнения параболы. При x=1 функция z = 25 + y². При y = 1, z = 25x² + 1. Если отсечь поверхность плоскостью Оxy, то получим эллипс. |
||||
Пример 2Если отсечь данную поверхность плоскостями Оzx, Ozy, то получим гиперболу, две части которой будут иметь общий максимум в точке х = 0 или y = 0. Т.е. если x или y примет какое-либо фиксированное значение, то функция примет вид: |
||||
Если отсечь поверхность плоскостью Оxy, то в зависимости от того чему равно z, сечение может принять разный график. Если z ≤ 1, то ветви гиперболы не соединяются на осях, если z > 1 — ветви соединяются на пересечении с осями x или y.
|
||||
Это объясняется тем, что левая часть равенства определена при любом значении х, если z > 1. И может быть не определена при определенном значении х, если z ≤ 1. Построение графика функции от двух переменных является довольно сложной задачей. Поэтому для построения такого графика функции используют сечения в плоскостях Ozx, Ozy и Oxy. |
||||
| 11 12 13 14 15 16 17 18 19 | ||||
Библиотека Matplotlib
Библиотека
matplotlib¶Есть несколько пакетов для построения графиков.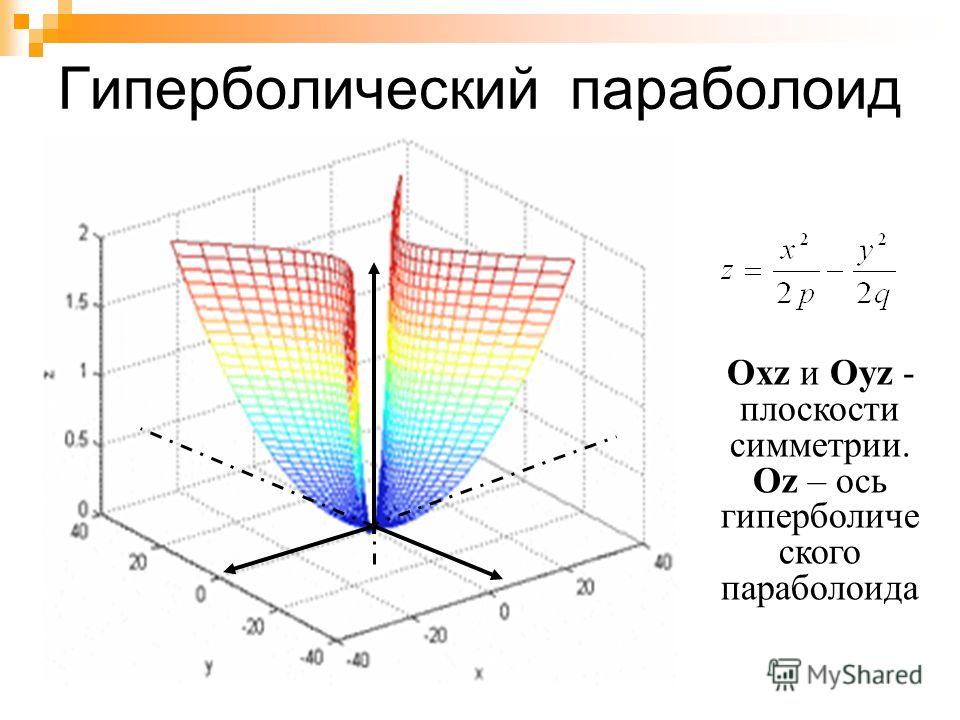 Один из наиболее популярных —
Один из наиболее популярных — matplotlib. Если в jupyter notebook выполнить специальную магическую команду %matplotlib inline, то графики будут строиться в том же окне браузера. Есть другие варианты, в которых графики показываются в отдельных окнах. Это удобно для трёхмерных графиков — тогда их можно вертеть мышкой (в случае inline графиков это невозможно). Графики можно также сохранять в файлы, как в векторных форматах (eps, pdf, svg), так и в растровых (png, jpg). matplotlib позволяет строить двумерные графики практически всех нужных типов, с достаточно гибкой регулировкой их параметров; он также поддерживает основные типы трёхмерных графиков, но для серьёзной трёхмерной визуализации данных лучше пользоваться более мощными специализированными системами.
Некоторые функции отрисовки
plt.scatter(x, y, params)— нарисовать точки с координатами из $x$ по горизонтальной оси и из $y$ по вертикальной оси;plt.— нарисовать график по точкам с координатами из $x$ по горизонтальной оси и из $y$ по вертикальной оси. Точки будут соединятся в том порядке, в котором они указаны в этих массивах;
plt.fill_between(x, y1, y2, params)— закрасить пространство между $y_1$ и $y_2$ по координатам из $x$;plt.pcolormesh(x1, x1, y, params)— закрасить пространство в соответствии с интенсивностью $y$;plt.contour(x1, x1, y, lines)— нарисовать линии уровня. Затем нужно применитьplt.clabel.
Вспомогательные функции
plt.figure(figsize=(x, y))— создать график размера $(x, y)$;plt.show()— показать график;plt.subplot(...)— добавить подграфик;plt.xlim(x_min, x_max)— установить пределы графика по горизонтальной оси;plt.ylim(y_min, y_max)— установить пределы графика по вертикальной оси;plt.— установить имя графика; title(name)
title(name)plt.xlabel(name)— установить название горизонтальной оси;plt.ylabel(name)— установить название вертикальной оси;plt.legend(loc=...)— сделать легенду в позиции loc;plt.grid()— добавить сетку на график;plt.savefig(filename)— сохранить график в файл.
http://matplotlib.org/gallery.html — тысячи примеров
У функций в matplotlib много параметров.
Для того, чтобы посмотреть все параметры, можно воспользоваться справкой, например,
plt.plot?
1. Простые графики¶
gnuplot / plot3d (1E)
В splot, нулевая точка оси Z размещается выше плоскости XY. Чтобы переместить начало координат на плоскость XY, используется set ticslevel . Когда ticslevel=0, ноль оси Z перемещается на плоскость XY.
gnuplot> set ticslevel 0 gnuplot> splot (x**2)*(y**2)
В 3D построении, размер ячейки (координата XY) определяется isosample. Чем меньше значение, тем толще сетка. По умолчанию это 10.
Чем меньше значение, тем толще сетка. По умолчанию это 10.
Если сетка координат слишком толстая, это может придать проблемы, когда скрытые линии установленны командой set hidden3d. Следующий пример показывает 3D построение функции z=sin(x)*cos(y) с isosample равным 10. Верхний рисунок без скрытого удаления, нижний с ним .
Чтобы избежать данной проблемы, устаноовите значение isosample больше. Далее установите его на 40. Чтобы сетки X и Y meshes различались, попробуйте set isosample 20,40.
gnuplot> set isosample 40
Точка обзора в 3D построениях контролируется командой set view. По умолчанию настройки:
gnuplot> show view
view is 60 rot_x, 30 rot_z, 1 scale, 1 scale_z
Изначально (перед вращением), экран параллелен плоскости XY и перпендикулярен оси Z.
Сначала, ось X вращается до 60 градусов (rot_x), затем наклон оси Z.
Далее, новая ось Z вращается до 30 градусов (rot_z). Это точка наблюдения которую splot использует по умолчанию.
Команда set view вращает график.
| Угол обзора 60,15 | |
| Угол обзора 60,45 | |
| Угол обзора 60,75 | |
| Угол обзора 15,30 |
Линиями уровня управляет команда set cntrparam.
gnuplot> set contour gnuplot> set cntrparam levels 10 gnuplot> set cntrparam levels incremental -1, 0.2, 1 gnuplot> set cntrparam levels discrete -0.2, -0.5, 0.2, 0.5
Пример выше показывает три способа управления контурами.
Ключевое слово levels определяет уровень контурных линий. Выше levels 10 показывет, что отображено 10 линий.
Далее, incremental определяет начальное, приращение, конечное значения. Так же можно определить высоту,
на которой будут отбражены линии, командой levels discrete.
Выше levels 10 показывет, что отображено 10 линий.
Далее, incremental определяет начальное, приращение, конечное значения. Так же можно определить высоту,
на которой будут отбражены линии, командой levels discrete.
Легенда для линий уровня размещается в легенде графика. Чтобы стереть легенду линий уровня, используется команда set noclabel . В данном примере контурные линии такие же, как и внешнии линии на построении.
Линии уровня далее будут использоваться на поверхности. Нет никакой возможности произвольно управлять видами линий. Придется использовать внешние инструменты, как наприемр Tgif, чтобы редактировать стиль линий.
Если точка обзора выше плоскости XY, то получаем контуры 2D построения. Сначала, устанавливаем точку обзора 0,0 при помощи set view 0,0 и указываем set nosurface, чтобы скрыть поверхность.
gnuplot> set contour base gnuplot> set nosurface gnuplot> set view 0,0
Точка обзора 60,30
Точка обзора 0,0
Ось Y становиться правосторонней командой set view 0,0. Если необходимо сделать ее левосторонней,
используется set view 180,180.
В этом методе подписи Y становятся горизонтальными. Если необходимо сделать их вертикальным, используется «table» как указанно ниже.
Если необходимо сделать ее левосторонней,
используется set view 180,180.
В этом методе подписи Y становятся горизонтальными. Если необходимо сделать их вертикальным, используется «table» как указанно ниже.
Можно сделать 2D построение лучше, используя терминал table. Контурные линии единожды пишутся в файле данных командой set term table, которая производит 2D данные различных контурных линий. См. пример в галерее.
gnuplot> set term table gnuplot> set output "table.dat" gnuplot> replot gnuplot> set output gnuplot> set term x11 gnuplot> plot "table.dat" using 1:2 with lines
[ver.4] ТОЛЬКО !
2D построение с цветной картой легко может быть сделано с терминалом pm3d.
2-1)Контурные линии наносятся на поверхность, затем поднимаются вверх. прямо до плоскости, а затем отображается в маленьком окошке с правой стороны.
 Отрицательные линии от кутур — красные,
положительный синий, а ноль — желтый.
Отрицательные линии от кутур — красные,
положительный синий, а ноль — желтый. Помимо полиномов, синус, косинус и экспоненциальные функции
ведут себя хорошо.
Вот поверхность:
z = sin (x + y)
Обратите внимание, что, удерживая x фиксированным, скажем, x = C, кривые
z = sin (C + y) — это просто сдвинутые синусоидальные кривые.
Вот график поверхности:
z = sin (xy), а также коробка для яиц:
г = грех (х) грех (у)
Рациональная функция — это отношение двух многочленов.2).
Верно ли, что если предел x стремится к нулю f (x, 0) равно 0, а предел, когда y стремится к нулю для f (0, y), равен нуль, то предел f (x, y), когда (x, y) переходит в (0,0), равен 0? ОТВЕЧАТЬ (другой вид с глазное яблоко в (6, -2,3) ОТВЕТ) Каков предел f (x, x), когда x стремится к 0?
Хорошо, предположим, что f (x, y) стремится к нулю на каждом луче
идет в (0,0). Конечно, этого достаточно, чтобы подразумевать, что
предел f (x, y) = 0, когда (x, y) переходит в (0,0)?
ОТВЕЧАТЬ
(другой вид с
глазное яблоко в (2,6,3) ОТВЕТ)
Желтая сетка — это поверхность {(x, y, z): y = x ^ 2}.
Исполняемый файл и источник: progs.zip. Эти программы написаны на TrueBasic для компьютеров MSDos. и заархивирован в архив с помощью PKZIP (используйте PKUNZIP) разархивировать.
Графики и кривые уровня
Графики и кривые уровняСреда, 25 февраля
Графики и кривые уровня
График функции f (x, y) — это набор всех точек (x, y, z) в пространстве такое, что (x, y) находится в области определения f и z = f (x, y). Вот несколько примеров. Пример 1. f (x, y) = x 2 + y 2 .
Пример 2. f (x, y) = x 2 -y 2 .
Пример 2. f (x, y) = e -x 2 -y 2 .
Пример 3. В примере в понедельник мы рассмотрели функцию стоимости
С (х, у) = 1200 / х + 1200 / у + 3xy. Его график показан ниже.
При виде сбоку кажется, что минимальное значение этой функции составляет около 500.
Пример 4. f (x, y) = 2e — (x + 1) 2 -y 2 + 3e — (x-2) 2 — (y-1) 2 -2e — (x-1) 2 — (y + 2) 2
f (x, y) = 2e — (x + 1) 2 -y 2 + 3e — (x-2) 2 — (y-1) 2 -2e — (x-1) 2 — (y + 2) 2
Уровень A кривая функции f (x, y) представляет собой набор точек (x, y) в плоскости такая, что f (x, y) = c для фиксированного значения c.
Пример 5. Кривые уровня f (x, y) = x 2 + y 2 являются кривыми
form x 2 + y 2 = c для различных вариантов c.Это круги радиуса квадратного корня из c. Некоторые из них показаны ниже.
Можно представить себе кривую уровня f (x, y) = c как
горизонтальное сечение графика на высоте z = c. Когда каждая кривая уровня f (x, y) = c является
построенный на высоте c единиц над плоскостью xy, мы получаем рисунок ниже.
Пример 6. Кривые уровня f (x, y) = x 2 -y 2 являются гиперболами.
Здесь они показаны на соответствующей высоте.
Пример 7. Кривые уровня f (x, y) = 2e — (x + 1) 2 -y 2 + 3e — (x-2) 2 — (y-1) 2 -2e — (x-1) 2 — (y + 2) 2 показаны ниже. Сравнивая с графиком в примере 4, мы видим, что точки (x, y), в которых f
имеет максимумы и минимумы в центрах круговых кривых уровня.
Пример 8. Вот кривые уровня для функции стоимости C (x, y) = 1200 / x + 1200 / y + 3xy.
Сравнивая с графиком в Примере 3, кажется, что
минимальное значение C (x, y) достигается примерно при (7.5,7,5).
Contour-XYData-ZLabel СводкаИз этого туториала Вы узнаете, как создать контур из данных XYZ и добавить значение Z в качестве метки для каждой точки данных XY. Что вы узнаетеИз этого туториала Вы узнаете, как
Ступени
|
Квадрические поверхности — Объем исчисления 3
Цели обучения
- Определите цилиндр как тип трехмерной поверхности.
- Распознавать основные особенности эллипсоидов, параболоидов и гиперболоидов.
- Используйте трассировки, чтобы нарисовать пересечения квадратичных поверхностей с координатными плоскостями.
Мы изучали векторы и векторные операции в трехмерном пространстве, и мы разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями , для изучения множества других поверхностей, которые могут быть построены в трехмерной системе координат.
Идентификационные цилиндры
Первая поверхность, которую мы рассмотрим, — это цилиндр. Хотя большинство людей сразу же думают о полой трубке или соломке с газировкой, когда слышат слово , цилиндр , здесь мы используем широкое математическое значение этого термина. Как мы видели, цилиндрические поверхности не обязательно должны быть круглыми. Прямоугольный нагревательный канал представляет собой цилиндр, как и свернутый коврик для йоги, поперечное сечение которого имеет форму спирали.
Хотя большинство людей сразу же думают о полой трубке или соломке с газировкой, когда слышат слово , цилиндр , здесь мы используем широкое математическое значение этого термина. Как мы видели, цилиндрические поверхности не обязательно должны быть круглыми. Прямоугольный нагревательный канал представляет собой цилиндр, как и свернутый коврик для йоги, поперечное сечение которого имеет форму спирали.
В двумерной координатной плоскости уравнение описывает круг с центром в начале координат и радиусом. В трехмерном пространстве это же уравнение представляет поверхность.Представьте себе копии круга, расположенные друг над другом с центром на оси z ((Рисунок)), образуя полую трубку. Затем мы можем построить цилиндр из набора прямых, параллельных оси z , проходящих через окружность в плоскости xy , как показано на рисунке. Таким образом, любую кривую в одной из координатных плоскостей можно продолжить, чтобы она стала поверхностью.
Определение
Набор линий, параллельных заданной линии, проходящей через заданную кривую, называется цилиндрической поверхностью или цилиндром. Параллельные линии называются линиями.
Из этого определения мы можем видеть, что у нас все еще есть цилиндр в трехмерном пространстве, даже если кривая не является окружностью. Любая кривая может образовывать цилиндр, и линейки, составляющие цилиндр, могут быть параллельны любой данной линии ((Рисунок)).
В трехмерном пространстве график уравнения представляет собой цилиндр или цилиндрическую поверхность с линиями, параллельными оси y .Графики цилиндрических поверхностей
Нарисуйте графики следующих цилиндрических поверхностей.
Нарисуйте или воспользуйтесь графическим инструментом для просмотра графика цилиндрической поверхности, определяемой уравнением
.
Подсказка
Переменная может принимать любое значение без ограничений.
При рисовании поверхностей мы увидели, что полезно рисовать пересечение поверхности с плоскостью, параллельной одной из координатных плоскостей. Эти кривые называются следами. Мы можем видеть их на графике цилиндра на (Рисунок).
Определение
Следы поверхности — это поперечные сечения, созданные, когда поверхность пересекает плоскость, параллельную одной из координатных плоскостей.
(a) Это один вид графика уравнения (b) Чтобы найти след графика на плоскости xz , установите След — это просто двумерная синусоида. Трассы полезны при рисовании цилиндрических поверхностей. Однако для цилиндра в трех измерениях полезен только один набор следов. Обратите внимание на (рисунок), что след графика на плоскости xz полезен при построении графика. Однако след на плоскости xy представляет собой просто серию параллельных линий, а след на плоскости yz — это просто одна линия.
Цилиндрические поверхности образованы набором параллельных линий. Однако не все поверхности в трех измерениях строятся так просто.Теперь мы исследуем более сложные поверхности, и следы являются важным инструментом в этом исследовании.
Квадрические поверхности
Мы узнали о трехмерных поверхностях, описываемых уравнениями первого порядка; это самолеты. Некоторые другие распространенные типы поверхностей можно описать уравнениями второго порядка. Мы можем рассматривать эти поверхности как трехмерные продолжения конических сечений, которые мы обсуждали ранее: эллипса, параболы и гиперболы. Мы называем эти графы квадратичными поверхностями.
Определение
Квадрические поверхности — это графики уравнений, которые могут быть выражены в форме
Когда квадратная поверхность пересекает координатную плоскость, след представляет собой коническое сечение.
Эллипсоид — это поверхность, описываемая уравнением вида Установить, чтобы увидеть след эллипсоида на плоскости yz . Чтобы увидеть следы в плоскостях y и xz , установите и соответственно. Обратите внимание, если след на плоскости xy представляет собой круг.Точно так же, если след на плоскости xz является кругом, а если тогда след на плоскости yz является кругом. Таким образом, сфера представляет собой эллипсоид с
Чтобы увидеть следы в плоскостях y и xz , установите и соответственно. Обратите внимание, если след на плоскости xy представляет собой круг.Точно так же, если след на плоскости xz является кругом, а если тогда след на плоскости yz является кругом. Таким образом, сфера представляет собой эллипсоид с
Набросок эллипсоида
Нарисуйте эллипсоид
След эллипсоида представляет собой эллипс в каждой из координатных плоскостей. Однако это не обязательно для всех квадратичных поверхностей. На многих квадратичных поверхностях есть следы, которые представляют собой различные виды конических сечений, и это обычно обозначается названием поверхности.Например, если поверхность может быть описана уравнением формы, мы называем эту поверхность эллиптическим параболоидом. Трасса на плоскости xy представляет собой эллипс, но следы на плоскости xz и yz являются параболами ((Рисунок)). Другие эллиптические параболоиды могут иметь другую ориентацию, просто меняя переменные местами, чтобы получить другую переменную в линейном члене уравнения или
Другие эллиптические параболоиды могут иметь другую ориентацию, просто меняя переменные местами, чтобы получить другую переменную в линейном члене уравнения или
Эта квадратичная поверхность называется эллиптическим параболоидом .
Идентификация следов квадратичных поверхностей
Описать следы эллиптического параболоида
Гиперболоиды одного листа обладают удивительными свойствами. Например, они могут быть построены с использованием прямых линий, как в скульптуре на (Рисунок) (а). Фактически градирни для атомных электростанций часто имеют форму гиперболоида. Строители могут использовать в конструкции прямые стальные балки, что делает башни очень прочными при использовании относительно небольшого количества материала ((Рисунок) (b)).
(a) Скульптура в форме гиперболоида может быть построена из прямых линий. (б) Градирни для атомных электростанций часто строятся в форме гиперболоида.
Вступление к главе: Поиск фокуса параболического отражателя
Энергия, падающая на поверхность параболического отражателя, концентрируется в фокусе отражателя ((Рисунок)).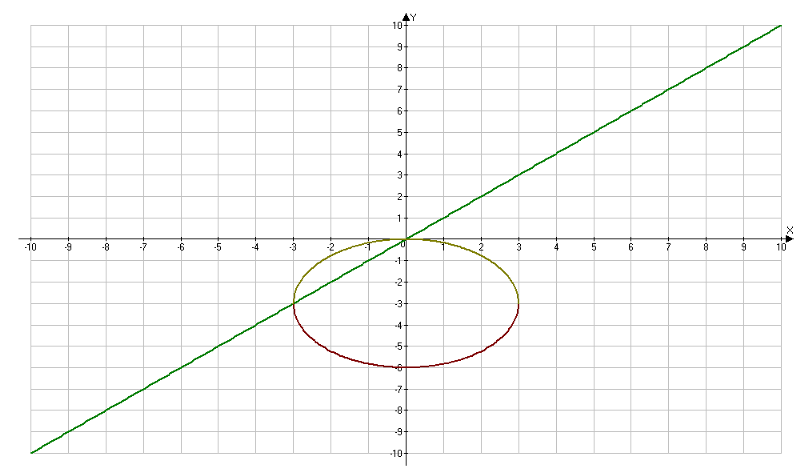 Если поверхность параболического отражателя описывается уравнением, где находится фокус отражателя?
Если поверхность параболического отражателя описывается уравнением, где находится фокус отражателя?
Энергия отражается от параболического отражателя и собирается в фокусной точке.(кредит: модификация CGP Gray, Wikimedia Commons)
Семнадцать стандартных квадратичных поверхностей могут быть получены из общего уравнения
На следующих рисунках приведены наиболее важные из них.
Характеристики общих квадратичных поверхностей: эллипсоид, гиперболоид одного листа, гиперболоид двух листов.
Характеристики общих квадратичных поверхностей: эллиптический конус, эллиптический параболоид, гиперболический параболоид.
Определение уравнений квадратичных поверхностей
Определите поверхности, представленные данными уравнениями.
Определите поверхность, представленную уравнением
Гиперболоид из одного листа с центром в
Подсказка
Посмотрите на знаки и силу терминов.
Ключевые понятия
- Набор линий, параллельных данной линии, проходящих через данную кривую, называется цилиндром или цилиндрической поверхностью . Параллельные линии называются постановлениями .
- Пересечение трехмерной поверхности и плоскости называется следом .Чтобы найти след в плоскостях xy -, yz — или xz , установите соответственно.
- Квадрические поверхности — это трехмерные поверхности со следами, состоящими из конических участков. Каждую квадратичную поверхность можно выразить уравнением вида
- Чтобы нарисовать график квадратичной поверхности, начните с рисования следов, чтобы понять структуру поверхности.
- Важные квадратичные поверхности приведены на (Рисунок) и (Рисунок).

4.4.1.1 Функции нескольких переменных — Исчисление Том 3
Цели обучения
- 4.1.1 Распознайте функцию двух переменных и определите ее область и диапазон.
- 4.1.2 Нарисуйте график функции двух переменных.
- 4.1.3 Нарисуйте несколько кривых или кривых уровня функции двух переменных.
- 4.1.4 Распознайте функцию трех или более переменных и определите ее поверхности уровня.
Наш первый шаг — объяснить, что такое функция более чем одной переменной, начиная с функций двух независимых переменных.Этот шаг включает в себя определение области и диапазона таких функций и обучение их построению в виде графиков. Мы также исследуем способы связать графики функций в трех измерениях с графиками более знакомых плоских функций.
Функции двух переменных
Определение функции двух переменных очень похоже на определение функции одной переменной. Основное отличие состоит в том, что вместо отображения значений одной переменной в значения другой переменной мы сопоставляем упорядоченные пары переменных с другой переменной.
Определение
Функция двух переменных z = f (x, y) z = f (x, y) отображает каждую упорядоченную пару (x, y) (x, y) в подмножестве DD реальной плоскости ℝ2ℝ2 в уникальное действительное число. zz Набор DD называется доменом функции. Диапазон числа ff — это набор всех действительных чисел zz, который имеет хотя бы одну упорядоченную пару (x, y) ∈D (x, y) ∈D такую, что f (x, y) = zf (x, y) = z, как показано на следующем рисунке.
Фигура 4.2 Область определения функции двух переменных состоит из упорядоченных пар (x, y).(х, у).Определение области определения функции двух переменных включает в себя учет любых ограничений области, которые могут существовать. Давайте взглянем.
Пример 4.1
Домены и диапазоны функций двух переменных
Найдите домен и диапазон каждой из следующих функций:
- f (x, y) = 3x + 5y + 2f (x, y) = 3x + 5y + 2
- г (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2
Решение
- Это пример линейной функции от двух переменных.
 Нет значений или комбинаций xx и yy, которые заставляют f (x, y) f (x, y) быть неопределенным, поэтому область определения ff равна ℝ2.ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно такое решение может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ.
Нет значений или комбинаций xx и yy, которые заставляют f (x, y) f (x, y) быть неопределенным, поэтому область определения ff равна ℝ2.ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно такое решение может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ. - Чтобы функция g (x, y) g (x, y) имела действительное значение, величина под квадратным корнем должна быть неотрицательной:
9-х2-у2≥0.9-х2-у2≥0.
Это неравенство можно записать в виде
Следовательно, область определения g (x, y) g (x, y) равна {(x, y) ∈ℝ2 | x2 + y2≤9}. {(X, y) ∈ℝ2 | x2 + y2≤9}. График этого набора точек можно описать как диск радиуса 33 с центром в начале координат. Область включает граничный круг, как показано на следующем графике.
Область включает граничный круг, как показано на следующем графике.
Фигура 4.3 Область определения функции g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 — замкнутый круг радиуса 3.
Чтобы определить диапазон значений g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2, мы начнем с точки (x0, y0) (x0, y0) на границе области, которое определяется соотношением x2 + y2 = 9. x2 + y2 = 9. Отсюда следует, что x02 + y02 = 9×02 + y02 = 9 и
g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−9 = 0. g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9− 9 = 0.
Если x02 + y02 = 0x02 + y02 = 0 (другими словами, x0 = y0 = 0), x0 = y0 = 0), то
g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−0 = 3.g (x0, y0) = 9 − x02 − y02 = 9− (x02 + y02) = 9−0 = 3.
Это максимальное значение функции. Учитывая любое значение c между 0 и 3,0 и 3, мы можем найти весь набор точек внутри области gg, таких что g (x, y) = c: g (x, y) = c:
9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2. 9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.
9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.
Поскольку 9 − c2> 0,9 − c2> 0, это описывает круг радиуса 9 − c29 − c2 с центром в начале координат. Любая точка на этой окружности удовлетворяет уравнению g (x, y) = c.g (x, y) = c. Следовательно, диапазон этой функции можно записать в интервальной записи как [0,3].[0,3].
Контрольно-пропускной пункт 4.1
Найдите область определения и диапазон функции f (x, y) = 36−9×2−9y2.f (x, y) = 36−9×2−9y2.
Графические функции двух переменных
Предположим, мы хотим построить график функции z = (x, y) .z = (x, y). Эта функция имеет две независимые переменные (xandy) (xandy) и одну зависимую переменную (z). (Z). При построении графика функции y = f (x) y = f (x) одной переменной мы используем декартову плоскость. Мы можем построить график любой упорядоченной пары (x, y) (x, y) на плоскости, и каждая точка на плоскости имеет связанную с ней упорядоченную пару (x, y) (x, y).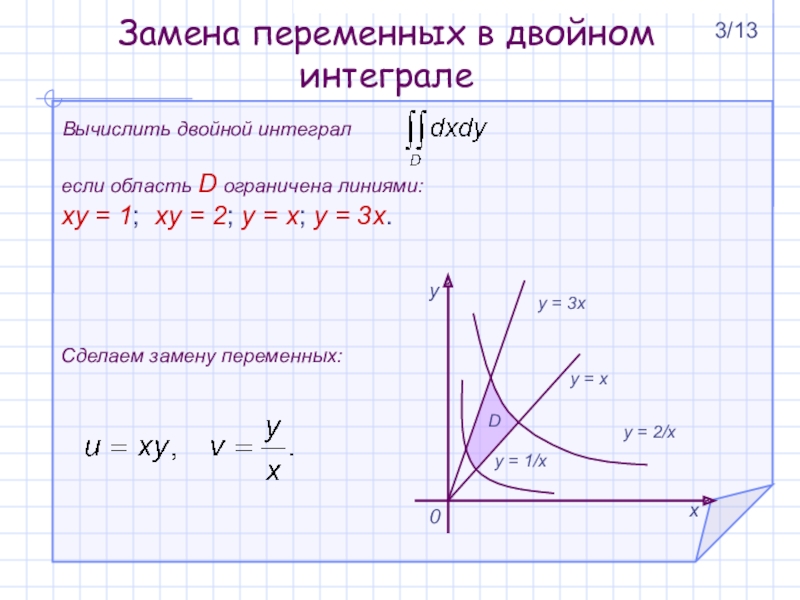 С функцией двух переменных каждая упорядоченная пара (x, y) (x, y) в области определения функции отображается в действительное число z.z. Следовательно, график функции ff состоит из упорядоченных троек (x, y, z). (X, y, z). График функции z = (x, y) z = (x, y) двух переменных называется поверхностью.
С функцией двух переменных каждая упорядоченная пара (x, y) (x, y) в области определения функции отображается в действительное число z.z. Следовательно, график функции ff состоит из упорядоченных троек (x, y, z). (X, y, z). График функции z = (x, y) z = (x, y) двух переменных называется поверхностью.
Чтобы более полно понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте плоскую систему координат (x, y) (x, y). Тогда каждая точка в области определения функции ff имеет уникальное значение z, связанное с ней.Если zz положительно, то графическая точка расположена выше xy-plane, xy-plane, если zz отрицательна, то графическая точка расположена ниже xy-plane.xy-plane. Набор всех нанесенных на график точек становится двумерной поверхностью, которая является графиком функции f.f.
Пример 4.2
Графические функции двух переменных
Создайте график каждой из следующих функций:
- г (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2
- f (x, y) = x2 + y2f (x, y) = x2 + y2
Решение
- В примере 4.
 1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
Фигура 4.4 График полушария представлен заданной функцией двух переменных.
- Эта функция также содержит выражение x2 + y2.х2 + у2. Приравнивая это выражение к различным значениям, начиная с нуля, мы получаем круги увеличивающегося радиуса. Минимальное значение f (x, y) = x2 + y2f (x, y) = x2 + y2 равно нулю (достигается, когда x = y = 0.). X = y = 0.). Когда x = 0, x = 0, функция становится z = y2, z = y2, а когда y = 0, y = 0, тогда функция становится z = x2.z = x2. Это сечения графика и параболы. Напомним из Введение в векторы в космосе, что имя графика f (x, y) = x2 + y2f (x, y) = x2 + y2 — это параболоид . График ff представлен на следующем графике.
Фигура 4.5 Параболоид — это график заданной функции двух переменных.
Пример 4.3
Гайки и болты
Функция прибыли для производителя оборудования задается
f (x, y) = 16− (x − 3) 2− (y − 2) 2, f (x, y) = 16− (x − 3) 2− (y − 2) 2,, где xx — количество гаек, проданных в месяц (в тысячах), а yy — количество болтов, проданных за месяц (в тысячах). Прибыль измеряется тысячами долларов.Нарисуйте график этой функции.
Прибыль измеряется тысячами долларов.Нарисуйте график этой функции.
Решение
Эта функция является полиномиальной функцией от двух переменных. Область ff состоит из пар координат (x, y) (x, y), которые дают неотрицательную прибыль:
16− (x − 3) 2− (y − 2) 2≥0 (x − 3) 2+ (y − 2) 2≤16− (x − 3) 2− (y − 2) 2≥0 (x −3) 2+ (y − 2) 2≤16.Это диск радиуса 44 с центром в точке (3,2). (3,2). Еще одно ограничение состоит в том, что оба xandyxandy должны быть неотрицательными. Когда x = 3x = 3 и y = 2, y = 2, f (x, y) = 16. f (x, y) = 16. Обратите внимание, что любое значение может быть нецелым числом; например, можно продать 2.52,5 тысячи орехов в месяц. Таким образом, область содержит тысячи точек, поэтому мы можем рассматривать все точки в пределах диска. Для любых z <16, z <16 мы можем решить уравнение f (x, y) = z: f (x, y) = z:
16− (x − 3) 2− (y − 2) 2 = z (x − 3) 2+ (y − 2) 2 = 16 − z. 16− (x − 3) 2− (y − 2) 2 = z (x − 3) 2+ (y − 2) 2 = 16 − z.
Поскольку z <16, z <16, мы знаем, что 16 − z> 0,16 − z> 0, поэтому предыдущее уравнение описывает круг радиуса 16 − z16 − z с центром в точке (3,2). ( 3,2). Следовательно. диапазон f (x, y) f (x, y) равен {z∈ℝ | z≤16}.{z∈ℝ | z≤16}. График f (x, y) f (x, y) также является параболоидом, и этот параболоид направлен вниз, как показано.
Фигура 4.6 График данной функции двух переменных также является параболоидом.
Кривые уровня
Если туристы идут по пересеченным тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются маршруты. Топографическая карта содержит изогнутые линии, называемые контурными линиями . Каждая горизонтальная линия соответствует точкам на карте, имеющим одинаковую высоту (Рисунок 4.7). Линия уровня функции двух переменных f (x, y) f (x, y) полностью аналогична контурной линии на топографической карте.
Фигура
4,7
а) Топографическая карта Башни Дьявола, штат Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены. Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены. Обратите внимание, что вершина башни имеет ту же форму, что и центр топографической карты.
Определение
Для данной функции f (x, y) f (x, y) и числа cc в диапазоне f, af кривая уровня функции двух переменных для значения cc определяется как набор точек, удовлетворяющих уравнение f (x, y) = c.е (х, у) = с.
Возвращаясь к функции g (x, y) = 9 − x2 − y2, g (x, y) = 9 − x2 − y2, мы можем определить кривые уровня этой функции. Диапазон gg — это закрытый интервал [0,3]. [0,3]. Сначала мы выбираем любое число в этом отрезке, например c = 2.c = 2. Кривая уровня, соответствующая c = 2c = 2, описывается уравнением
9 − x2 − y2 = 2,9 − x2 − y2 = 2.Для упрощения возведем в квадрат обе части этого уравнения:
9-х2-у2 = 4,9-х2-у2 = 4.Теперь умножьте обе части уравнения на −1−1 и прибавьте 99 к каждой стороне:
Это уравнение описывает окружность с центром в начале координат и радиусом 5. 5. Использование значений cc между 0 и 30 и 3 дает другие круги также с центром в начале координат. Если c = 3, c = 3, то круг имеет радиус 0,0, поэтому он состоит исключительно из начала координат. Рисунок 4.8 представляет собой график кривых уровня этой функции, соответствующих c = 0,1,2 и 3.c = 0,1,2 и3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат. Здесь дело обстоит не так, потому что диапазон функции квадратного корня неотрицателен.
5. Использование значений cc между 0 и 30 и 3 дает другие круги также с центром в начале координат. Если c = 3, c = 3, то круг имеет радиус 0,0, поэтому он состоит исключительно из начала координат. Рисунок 4.8 представляет собой график кривых уровня этой функции, соответствующих c = 0,1,2 и 3.c = 0,1,2 и3. Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат. Здесь дело обстоит не так, потому что диапазон функции квадратного корня неотрицателен.
График различных кривых уровня функции называется контурной картой.
Пример 4.4
Создание контурной карты
Для функции f (x, y) = 8 + 8x − 4y − 4×2 − y2, f (x, y) = 8 + 8x − 4y − 4×2 − y2 найти кривую уровня, соответствующую c = 0. c = 0. Затем создайте контурную карту для этой функции. Каковы домен и диапазон f? F?
c = 0. Затем создайте контурную карту для этой функции. Каковы домен и диапазон f? F?
Решение
Чтобы найти кривую уровня для c = 0, c = 0, мы полагаем f (x, y) = 0f (x, y) = 0 и решаем.Это дает
0 = 8 + 8x − 4y − 4×2 − y2.0 = 8 + 8x − 4y − 4×2 − y2.Затем возводим обе части в квадрат и умножаем обе части уравнения на −1: −1:
. 4×2 + y2−8x + 4y − 8 = 0,4×2 + y2−8x + 4y − 8 = 0.Теперь мы переставляем члены, складывая члены xx вместе и члены yy вместе, и добавляем 88 к каждой стороне:
4×2−8x + y2 + 4y = 8.4×2−8x + y2 + 4y = 8.Затем мы группируем пары терминов, содержащих одну и ту же переменную в круглых скобках, и множим 44 из первой пары:
4 (x2−2x) + (y2 + 4y) = 8,4 (x2−2x) + (y2 + 4y) = 8.Затем мы заполняем квадрат в каждой паре круглых скобок и добавляем правильное значение в правую часть:
4 (x2−2x + 1) + (y2 + 4y + 4) = 8 + 4 (1) +4,4 (x2−2x + 1) + (y2 + 4y + 4) = 8 + 4 (1) +4.
Затем мы разлагаем левую часть на множители и упрощаем правую часть:
4 (x − 1) 2+ (y + 2) 2 = 16,4 (x − 1) 2+ (y + 2) 2 = 16.Наконец, делим обе стороны на 16:16:
(x − 1) 24+ (y + 2) 216 = 1. (x − 1) 24+ (y + 2) 216 = 1.(4.1)
Это уравнение описывает эллипс с центром в точке (1, −2). (1, −2). График этого эллипса представлен на следующем графике.
Фигура 4.9 Кривая уровня функции f (x, y) = 8 + 8x − 4y − 4×2 − y2f (x, y) = 8 + 8x − 4y − 4×2 − y2, соответствующая c = 0.c = 0.Мы можем повторить тот же вывод для значений cc меньше 4.4. Тогда уравнение 4.1 принимает вид
. 4 (x − 1) 216 − c2 + (y + 2) 216 − c2 = 14 (x − 1) 216 − c2 + (y + 2) 216 − c2 = 1для произвольного значения c.c. На рисунке 4.10 показана контурная карта для f (x, y) f (x, y) с использованием значений c = 0,1,2 и 3.c = 0,1,2 и 3. Когда c = 4, c = 4, кривая уровня представляет собой точку (−1,2). (- 1,2).
Фигура 4.10 Контурная карта для функции f (x, y) = 8 + 8x − 4y − 4×2 − y2f (x, y) = 8 + 8x − 4y − 4×2 − y2 с использованием значений c = 0,1,2,3 и 4 . c = 0,1,2,3 и 4.
c = 0,1,2,3 и 4.Контрольно-пропускной пункт 4.2
Найдите и изобразите линию уровня функции g (x, y) = x2 + y2−6x + 2yg (x, y) = x2 + y2−6x + 2y, соответствующую c = 15.c = 15.
Еще один полезный инструмент для понимания графика функции двух переменных называется вертикальной трассой. Кривые уровня всегда отображаются в плоскости xy, плоскости xy, но, как следует из их названия, вертикальные кривые отображаются в плоскостях xzxz или yz.yz-самолеты.
Определение
Рассмотрим функцию z = f (x, y) z = f (x, y) с областью определения D⊆ℝ2.D⊆ℝ2. Вертикальный след функции может быть либо набором точек, который решает уравнение f (a, y) = zf (a, y) = z для данной константы x = ax = a, либо f (x, b) = zf (x, b) = z для данной константы y = by = b.
Пример 4.5
Поиск вертикальных следов
Найдите вертикальные следы для функции f (x, y) = sinxcosyf (x, y) = sinxcosy, соответствующей x = −π4,0, и π4, x = −π4,0, и π4, и y = −π4,0, и π4. y = −π4,0 и π4.
y = −π4,0 и π4.
Решение
Сначала установите x = −π4x = −π4 в уравнении z = sinxcosy: z = sinxcosy:
z = sin (−π4) cosy = −2cosy2≈ − 0,7071cosy. z = sin (−π4) cosy = −2cosy2≈ − 0,7071cosy.Это описывает косинусный граф в плоскости x = −π4.x = −π4. Остальные значения zz представлены в следующей таблице.
| куб.см | Вертикальный след для x = cx = c |
|---|---|
| −π4 − π4 | z = −2cosy2z = −2cosy2 |
| 00 | z = 0z = 0 |
| π4π4 | z = 2cosy2z = 2cosy2 |
 1
Вертикальные трассы, параллельные плоскости xz, xz, для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
1
Вертикальные трассы, параллельные плоскости xz, xz, для функции f (x, y) = sinxcosyf (x, y) = sinxcosyАналогичным образом мы можем подставить значения y в уравнение f (x, y) f (x, y), чтобы получить трассы в плоскости yz, плоскости yz, как указано в следующей таблице. .
| dd | Вертикальный след для y = dy = d |
|---|---|
| −π4 − π4 | z = 2sinx2z = 2sinx2 |
| 00 | z = sinxz = sinx |
| π4π4 | z = 2sinx2z = 2sinx2 |
 2
Вертикальные трассы, параллельные плоскости yz-Planeyz для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
2
Вертикальные трассы, параллельные плоскости yz-Planeyz для функции f (x, y) = sinxcosyf (x, y) = sinxcosyТри трассы в плоскости xz-planexz являются косинусоидальными функциями; три следа в плоскости yz-planeyz являются синусоидальными функциями. Эти кривые появляются на пересечениях поверхности с плоскостями x = −π4, x = 0, x = π4x = −π4, x = 0, x = π4 и y = −π4, y = 0, y = π4y = — π4, y = 0, y = π4, как показано на следующем рисунке.
Фигура 4.11 Вертикальные следы функции f (x, y) f (x, y) представляют собой косинусоидальные кривые в плоскостях xz, плоскостях xz (a) и синусоидальные кривые в плоскостях yz, плоскостях yz (b).Контрольно-пропускной пункт 4.3
Определите уравнение вертикального следа функции g (x, y) = — x2 − y2 + 2x + 4y − 1g (x, y) = — x2 − y2 + 2x + 4y − 1, соответствующего y = 3, y = 3, и описать его график.
Функции двух переменных могут создавать поразительные поверхности. На следующем рисунке показаны два примера.
Фигура 4,12 Примеры поверхностей, представляющих функции двух переменных: (а) комбинация степенной функции и синусоидальной функции и (б) комбинация тригонометрических, экспоненциальных и логарифмических функций.
Функции более двух переменных
До сих пор мы рассматривали только функции двух переменных. Однако полезно кратко рассмотреть функции более чем двух переменных. Два таких примера:
f (x, y, z) = x2−2xy + y2 + 3yz − z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных) f (x, y, z) = x2−2xy + y2 + 3yz− z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных)и
g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost. g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost.В первой функции (x, y, z) (x, y, z) представляет точку в пространстве, а функция ff сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра.Во второй функции (x, y) (x, y) может представлять точку на плоскости, а tt может представлять время. Функция может отображать точку на плоскости с третьей величиной (например, давлением) в данный момент времени t.t. Метод поиска области определения функции более двух переменных аналогичен методу для функций одной или двух переменных.
Пример 4.6
Домены для функций трех переменных
Найдите домен каждой из следующих функций:
- f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2
- г (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2
Решение
- Для определения функции f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2 (и реальное значение) должны выполняться два условия:
- Знаменатель не может быть нулевым.
- Подкоренное выражение не может быть отрицательным.
9 − x2 − y2 − z2> 0,9 − x2 − y2 − z2> 0.
Перемещение переменных на другую сторону и изменение неравенства дает домен как
. область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9}, область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9},
который описывает шар радиуса 33 с центром в начале координат. ( Примечание : Поверхность шара не входит в этот домен.) - Чтобы функция g (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2 была определена (и была действительным значением), должны выполняться два условия:
- Подкоренное выражение не может быть отрицательным.
- Знаменатель не может быть нулевым.
область (g) = {(x, y, t) | y ≠ ± x, t≥2}. область (g) = {(x, y, t) | y ≠ ± x, t≥2}.
Контрольно-пропускной пункт 4.4
Найти область определения функции h (x, y, t) = (3t − 6) y − 4×2 + 4.ч (х, у, т) знак равно (3т-6) у-4х2 + 4.
Функции двух переменных имеют кривые уровня, которые показаны в виде кривых на плоскости xy-plane.xy-plane. Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Определение
Для функции f (x, y, z) f (x, y, z) и числа cc в диапазоне f, f поверхность уровня функции трех переменных определяется как набор точек, удовлетворяющих уравнение f (x, y, z) = c.е (х, у, г) = с.
Пример 4,7
Поиск ровной поверхности
Найдите поверхность уровня для функции f (x, y, z) = 4×2 + 9y2 − z2f (x, y, z) = 4×2 + 9y2 − z2, соответствующей c = 1.c = 1.
Решение
Поверхность уровня определяется уравнением 4×2 + 9y2 − z2 = 1,4×2 + 9y2 − z2 = 1. Это уравнение описывает гиперболоид из одного листа, как показано на следующем рисунке.
Фигура 4,13 Гиперболоид из одного листа с некоторыми его плоскими поверхностями.
Контрольно-пропускной пункт 4.5
Найдите уравнение поверхности уровня функции
g (x, y, z) = x2 + y2 + z2−2x + 4y − 6zg (x, y, z) = x2 + y2 + z2−2x + 4y − 6z., что соответствует c = 2, c = 2, и, если возможно, опишите поверхность.
Раздел 4.1 Упражнения
В следующих упражнениях оцените каждую функцию по указанным значениям.
1 .W (x, y) = 4×2 + y2.W (x, y) = 4×2 + y2. Найдите W (2, −1), W (2, −1), W (−3,6) .W (−3,6).
2 .Вт (х, у) = 4×2 + y2.W (х, у) = 4х2 + у2. Найдите W (2 + h, 3 + h). W (2 + h, 3 + h).
3 .Объем правого кругового цилиндра вычисляется функцией двух переменных: V (x, y) = πx2y, V (x, y) = πx2y, где xx — радиус правого кругового цилиндра, а yy — высота. цилиндра. Оцените V (2,5) V (2,5) и объясните, что это означает.
4 .Кислородный баллон состоит из правого цилиндра высотой yy и радиуса xx с двумя полусферами радиуса xx, установленными наверху и внизу цилиндра.Выразите объем резервуара как функцию двух переменных, xandy, xandy, найдите V (10,2), V (10,2) и объясните, что это означает.
Для следующих упражнений найдите домен функции.
5 .V (x, y) = 4×2 + y2 V (x, y) = 4×2 + y2
6 .f (x, y) = x2 + y2−4f (x, y) = x2 + y2−4
7 .f (x, y) = 4ln (y2 − x) f (x, y) = 4ln (y2 − x).
8 .g (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2.
9 .z (x, y) = y2 − x2z (x, y) = y2 − x2
Найдите диапазон функций.
11 .g (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2.
12 .V (x, y) = 4×2 + y2 V (x, y) = 4×2 + y2
Для следующих упражнений найдите кривые уровня каждой функции при указанном значении cc, чтобы визуализировать данную функцию.
14 .z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 1c = 1
15 .z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 4c = 4
16 .g (x, y) = x2 + y2; c = 4, c = 9 g (x, y) = x2 + y2; c = 4, c = 9
17 .g (x, y) = 4 − x − y; c = 0,4 g (x, y) = 4 − x − y; c = 0,4
18 .f (x, y) = xy; c = 1; c = −1 f (x, y) = xy; c = 1; c = −1
19 .h (x, y) = 2x − y; c = 0, −2,2 h (x, y) = 2x − y; c = 0, −2,2
20 .f (x, y) = x2 − y; c = 1,2 f (x, y) = x2 − y; c = 1,2
21 год .g (x, y) = xx + y; c = −1,0,2 g (x, y) = xx + y; c = −1,0,2
22 .g (x, y) = x3 − y; c = −1,0,2 g (x, y) = x3 − y; c = −1,0,2
23 .g (x, y) = exy; c = 12,3 g (x, y) = exy; c = 12,3
24 .f (x, y) = x2; c = 4,9 f (x, y) = x2; c = 4,9
25 .f (x, y) = xy − x; c = −2,0,2 f (x, y) = xy − x; c = −2,0,2
26 .h (x, y) = ln (x2 + y2); c = −1,0,1 h (x, y) = ln (x2 + y2); c = −1,0,1
27 .g (x, y) = ln (yx2); c = −2,0,2 g (x, y) = ln (yx2); c = −2,0,2
28 год .z = f (x, y) = x2 + y2, z = f (x, y) = x2 + y2, c = 3c = 3
29 .f (x, y) = y + 2×2, f (x, y) = y + 2×2, c = c = любая константа
Для следующих упражнений найдите вертикальные кривые функций при указанных значениях xx и y и постройте кривые.
30 .z = 4 − x − y; x = 2z = 4 − x − y; x = 2
31 год .f (x, y) = 3x + y3, x = 1 f (x, y) = 3x + y3, x = 1
32 .z = cosx2 + y2z = cosx2 + y2 x = 1x = 1
Найдите домен следующих функций.
33 .z = 100−4×2−25y2z = 100−4×2−25y2
35 год .f (x, y, z) = 136−4×2−9y2 − z2f (x, y, z) = 136−4×2−9y2 − z2.
36 .f (x, y, z) = 49 − x2 − y2 − z2f (x, y, z) = 49 − x2 − y2 − z2.
37 .f (x, y, z) = 16 − x2 − y2 − z23f (x, y, z) = 16 − x2 − y2 − z23.
38 .f (x, y) = cosx2 + y2f (x, y) = cosx2 + y2
Постройте график функции для следующих упражнений.
39 .z = f (x, y) = x2 + y2z = f (x, y) = x2 + y2.
41 год .Используйте технологию для построения графика z = x2y.z = x2y.
Нарисуйте следующее, найдя кривые уровня. Проверить график, используя технологию.
42 .f (x, y) = 4 − x2 − y2f (x, y) = 4 − x2 − y2.
43 год .f (x, y) = 2 − x2 + y2f (x, y) = 2 − x2 + y2.
44 год .z = 1 + e − x2 − y2z = 1 + e − x2 − y2
47 .Опишите изолинии для нескольких значений cc для z = x2 + y2−2x − 2y.z = x2 + y2−2x − 2y.
Найдите поверхность уровня для функций трех переменных и опишите ее.
48 .w (x, y, z) = x − 2y + z, c = 4 w (x, y, z) = x − 2y + z, c = 4
49 .w (x, y, z) = x2 + y2 + z2, c = 9 w (x, y, z) = x2 + y2 + z2, c = 9
50 .w (x, y, z) = x2 + y2 − z2, c = −4w (x, y, z) = x2 + y2 − z2, c = −4
51 .w (x, y, z) = x2 + y2 − z2, c = 4 w (x, y, z) = x2 + y2 − z2, c = 4
52 .w (x, y, z) = 9×2−4y2 + 36z2, c = 0 w (x, y, z) = 9×2−4y2 + 36z2, c = 0
Для следующих упражнений найдите уравнение кривой уровня ff, которое содержит точку P.P.
53 .f (x, y) = 1−4×2 − y2, P (0,1) f (x, y) = 1−4×2 − y2, P (0,1)
54 .g (x, y) = y2arctanx, P (1,2) g (x, y) = y2arctanx, P (1,2)
55 .g (x, y) = exy (x2 + y2), P (1,0) g (x, y) = exy (x2 + y2), P (1,0)
56 .Напряженность EE электрического поля в точке (x, y, z) (x, y, z), возникающего в результате бесконечно длинного заряженного провода, лежащего вдоль оси y, определяется как E (x, y, z) = k / x2 + y2, E (x, y, z) = k / x2 + y2, где kk — положительная постоянная. Для простоты положим k = 1k = 1 и найдем уравнения поверхностей уровня для E = 10 и E = 100, E = 10 и E = 100.
57 год .Тонкая пластина из железа расположена в плоскости xy.xy-плоскость. Температура TT в градусах Цельсия в точке P (x, y) P (x, y) обратно пропорциональна квадрату ее расстояния от начала координат. Выразите TT как функцию от xandy.xandy.
58 .Обратитесь к предыдущей проблеме. Используя найденную там температурную функцию, определите константу пропорциональности, если температура в точке P (1,2) составляет 50 ° C, P (1,2) составляет 50 ° C. Используйте эту константу, чтобы определить температуру в точке Q (3,4) .Q (3,4).
59 .Обратитесь к предыдущей проблеме.Найдите кривые уровня для T = 40 ° C и T = 100 ° C, T = 40 ° C и T = 100 ° C и опишите, что представляют собой кривые уровня.
F x y xy graph
Разместите свои комментарии?
F (x, y) = xy — GeoGebra
5 часов назад f ( x , y ) = xy с контурами. Новые ресурсы.探究 位 似的 性质 ((制作 : 王权 龙 , 修订 : 孟宝兴)
Расчетное время чтения: 1 мин.
Веб-сайт: Geogebra.org
Категория 3: Используйте слова в предложении
Виджеты WolframAlpha: «Поверхностный график f (x, y)» Бесплатно
Только сейчас Получите бесплатный виджет «Поверхностный график f ( x , y )» для своего веб-сайта, блога, WordPress, Blogger , или iGoogle.Найдите больше инженерных виджетов в WolframAlpha.
Веб-сайт: Wolframalpha.com
Категория : Использование в предложении
Бесплатно, Для, Найти
Пример: Найти градиент функции f (x, y) = xy YouTube
3 часа назад В этом видео объясняется, как найти градиент функции двух переменных. Значение градиента объясняется и отображается графически. Сайт: http: // ma
Веб-сайт: Youtube.com
Категория : Использование в предложении
Найти, функция
График z = f (x, y) — GeoGebra
5 часов назад График z = f ( x , y ) Новые ресурсы. Open Middle: Системы линейных уравнений (2) Запись функций абсолютных значений из графиков
Расчетное время чтения: 1 мин.
Веб-сайт: Geogebra.org
Категория : Использование in a предложение
Функции, из
Как построить график функции af (x, y)? Ответы MATLAB…
4 часа назад летом я прошел курс Matlab, и теперь у меня graph проблема в исчислении.2. Должен ли я открывать функцию или я могу просто использовать команду со сценарием?
Веб-сайт: Mathworks.com
Категория : использовать в предложении
Функция
Как построить график функций f (xy)
6 часов назад Как построить график f ( xy ) функции 4.1.1. Распознавать функцию двух переменных и определять ее домен и диапазон. 4.1.2 Нарисуйте график функции двух переменных.4.1.3 Нарисуйте несколько кривых или кривых уровня функции двух переменных. 4.1.4 Распознать функцию…
Веб-сайт: Xubajibagi.weebly.com
Категория : использовать в предложении
Функции, функция
График f (x) = y Mathway
5 часов назад График f ( x ) = y . Объявление функции зависит от, но функция ввода содержит только переменную. Предполагать .Перепишите функцию в виде уравнения. Используйте…
Веб-сайт: Mathway.com
Категория : Используйте слова в предложении
Функция
Визуализация частных производных fxx, fyy, fxy и fyx
4 часа назад График z = f ( x , y ) требует трех измерений: два для домена и одно для диапазона . Используя мой пример f ( x , y ) = 2x 3 y 2, можете ли вы получить график этой функции? Если это так, вы также должны иметь возможность graph f x ( x , y ) = 6x 2 y 2 и f xy ( x , y ) = 12x 2 y .
Веб-сайт: Physicsforums.com
Категория : Использование и в предложении
Для, Функция
Кривые уровня Техасский университет в Остине
7 часов назад Кривые уровня. Два основных способа визуализации функций двух переменных — это графиков, и кривых уровня. Оба были представлены в более раннем учебном модуле. Кривые уровня: для функции z = f ( x , y ): D ⊆ R 2 → R кривая уровня значения c — это кривая C в D ⊆ R 2, на которой f C = c .Обратите внимание на критическую разницу между кривой уровня C
Веб-сайт: Web.ma.utexas.edu
Категория : Использование в предложении
Функции, Для, Функция
Решено = 7. Подсчитать объем региона под
8 часов назад Проблема решена! Это лучший ответ, основанный на отзывах и рейтингах. Транскрибированный текст изображения: = 7. Вычислите объем области под графиком из f ( x , y ) = xy и выше треугольной области на плоскости xy , которая имеет вершины в (0,0,0), (0,2,0) и (1,3,0).
Веб-сайт: Chegg.com
Категория : Использование в предложении
Обратная связь
Раздел 14.1 Функции двух переменных
4 часа назад Напомним, что график функции f одной переменной — это кривая y = f ( x ) на плоскости xy , состоящей из точек ( x , y ) с x в области функции и y = f ( x ).График функции двух переменных — это поверхность в трехмерном пространстве. 270
Веб-сайт: Math.ucsd.edu
Категория : Использование в предложении
Функция
График f (x, y) функция MATLAB отвечает MATLAB Central
5 часов назад Здравствуйте ! У меня на графике проблема в Nebulous Logic с Matlab. Я плохо разбираюсь в своих командах (никогда раньше не использовал Matlab, поэтому я не уверен, какую команду использовать.2. Мне нужно рассмотреть интервал [-10,10] и построить пять нечетких множеств (C1, C2, C3, C4, C5) для каждого из них.
Веб-сайт: Mathworks.com
Категория : Используйте слова в предложении
Функция, пять, нечеткая, для
Дифференциация функций с несколькими переменными
5 часов назад 959 функция f ( x , y ) с областью D представляет собой набор точек ( x , y , z) в пространстве, такое что z = f ( x , y ) , ( x , y ) ∈ D.Область D — это набор точек на плоскости xy . График затем получается путем перемещения каждой точки D параллельно оси z на величину, равную соответствующему значению функции z = f ( x , y ). Если D является частью
Веб-сайт: People.clas.ufl.edu
Категория : Использование в предложении
Функция
Математика 6 Exeter
7 часов назад The График уравнения y = f ( x ) представляет собой кривую на плоскости xy .С другой стороны, график уравнения z = f ( x ; y ) представляет собой поверхность в xyz-пространстве. Знакомый пример — это график z = p 9 2×2 y , который представляет собой полусферу радиуса 3. Для каких точек ( x ; y ) определена эта функция (и поверхность)? Найдите уравнение для плоскости, которая касается плоскости
Веб-сайт: Exeter.edu
Категория : Используйте слова в предложении
Знакомый, Для, Функция, Найти
Параметрические поверхности, часть 1 Университет Дьюка
2 часа назад Каждую поверхность, которая является графиком функции f ( x , y ), также можно описать параметрически, задав параметры x и y .На вашем рабочем листе убедитесь, что поверхность седла, которая представляет собой график из f ( x , y ) = xy , такая же, как график из r (u, v) = ui + vj + увк.
Веб-сайт: Services.math.duke.edu
Категория : Используйте слова в предложении
Функция
Генератор графов функций Онлайн калькулятор
2 часа назад В общем, до граф функция, таблица создается со значениями ( x , y ), а затем значения представлены в декартовой системе координат.3 + 2x Выберем случайные значения для столбца x ..
Веб-сайт: Calc-online.xyz
Категория : Используйте слова в предложении
Функция, для
Графики Equations University of Georgia
Just Now График из xy = x + y показан красным, тогда как график из xy = 2x + 2y показан зеленым. Два графика похожи в том, что они оба пересекают ось y в точке 0; однако они отличаются тем, что xy = x + y асимптотичен прямой y = 1 и xy = 2x + 2y асимптотичен прямой y = 2 (показано выше в синий).
Веб-сайт: Jwilson.coe.uga.edu
Категория : Использование в предложении
Unizor Algebra Graph F (x, y) YouTube
3 часа назад В общем, мы можем расширить определение графика функции набора точек с координатами ( x , y ), которые удовлетворяют уравнению F ( x , y ) = 0, где F
Веб-сайт: Youtube.com
Категория : Используйте слова в предложении
Функция
Каковы экстремумы и седловые точки f (x, y) = xy (1x
3 часа назад Объяснение: Мы можем расширить f от до f (x, y ) = xy — x2y — xy2. Затем найдите частные производные и установите их равными нулю. Очевидно, ( x , y ) = (0,0) , (1,0) и (0,1) являются решениями этой системы, а также критическими точками f .Другое решение можно найти из системы 1 −2x — y = 0, 1 — x — 2y = 0. Решение первого уравнения для
Веб-сайт: Socratic.org
Категория : Используйте и в предложении
Найти, найти, от, сначала, для
Решено Рассмотрим следующую функцию. f (x, y) = x2 + xy
8 часов назад ( x , y ) = f ( x , y ) = sex ( x , y ) = xy ( x , y ) = fyy ( x ,) = Найдите критическую точку.( x , y ) = — ([Найдите локальные максимальные и минимальные значения и седловые точки функции. Вам рекомендуется использовать калькулятор или компьютер, чтобы построить график функции с областью и точкой обзора который раскрывает все…
Веб-сайт: Chegg.com
Категория : Используйте слова в предложении
Fyy, Find, Function
Solve f (x + y) + f (xy) = 2f (x) + 2f (y) Microsoft Math Solver
5 часов назад Предположим, что (1) f ( x + y ) + f ( xy ) = f ( x ) + f ( y ) + f ( x ) f ( y ) для всех x , y \ in \ mathbb {R}.Как уже заметили другие, очевидным решением является f \ Equiv 0, поэтому мы предполагаем, что с этого момента f является рефлексивным: каждый, кто посетил веб-страницу a, также посетил веб-страницу b, для всех веб-страниц
Веб-сайт: Mathsolver.microsoft.com
Категория : Используйте слова в предложении
For, From
Как построить график уравнения F [x, y] = 0? Онлайн
9 часов назад Для каждого заданного y мне нужно решить это уравнение, т.е.2 + грех ( ху ). Если y и x …
Веб-сайт: Community.wolfram.com
Категория : Используйте to в предложении
For, Find, From
Университет линейных приближений Пенсильвании
5 часов назад Покажите, что f ( x , y ) = xe xy дифференцируемо в (1, 0), и найдите там свою линеаризацию. Затем используйте его, чтобы приблизить f (1.1, –0,1). Пример 2 ЛИНЕЙНЫЕ ПРИБЛИЖЕНИЯ Частные производные: fx ( x , y ) = exy + xye xy fy ( x , y ) = x2exy fx (1, 0) = 1 fy (1, 0) = 1 И fx, и fy — непрерывные функции. Итак, f дифференцируем по теореме 8.
Веб-сайт: Www2.math.upenn.edu
Категория : использование в предложении
Find, Fx, Fy, Functions
Построение графика функции f (x, y) двух переменных
2 часа назад Таким образом, « x 2 + y 2» записывается « x * x + y * y » или « x ^ 2 + y ^ 2″.[2] Например, f ( x , y ) = x 2 + y 2 будет отображено в виде графика, как на изображении ниже. [3] Вы можете сохранить изображение graph как файл на вашем ПК: это займет около 35 КБ.
Веб-сайт: Math.uww.edu
Категория : Используйте a в предложении
For, File
Активные производные второго порядка
7 часов назад Есть четыре частичных производных второго порядка производные функции f двух независимых переменных x и y : fxx = (fx) x , fxy = (fx) y , fyx = (fy) x и fyy = ( fy) y .2) {/ eq} предоставляется
Веб-сайт: Study.com
Категория : Использование в предложении
Кривые уровня Техасский университет в Остине
7 часов назад Кривые уровня. Для общей функции z = f ( x , y ) горизонтальное срезание является особенно важной идеей: Кривые уровня: для функции z = f ( x , y ): D ⊆ R 2 → R кривая уровня значения c — это кривая C в D ⊆ R 2, на которой f C = c.Обратите внимание на критическую разницу между уровнями…
Веб-сайт: Web.ma.utexas.edu
Категория : Использование в предложении
For, Function
Joint and Marginal Distributions
8 часов назад 0 0,2 0,4 0,6 0,8 1 0,2 0,4 0,6 0,8 1 0 0,5 1 1,5 2 2,5 yxf X , Y ( x , y ) Рисунок 1: График плотности f X , Y ( x , y ) = 4 ( xy + x + y ) / 5, 0 ≤ x , y ≤ 1 R ∞ −∞ R ∞ −∞ f X , Y ( x , y ) dydx = 1.Пример 5. Пусть ( X , Y ) имеет плотность стыков
Веб-сайт: Math.arizona.edu
Категория : Использование и в предложении
Рисунок
Математика 314 Лекция # 11 14.1: Функции нескольких переменных
Just Now График функции w = f ( x , y , z) трех переменных лежит в 4-мерном пространстве, поэтому мы не будем попытаться отобразить его график .Поверхности уровня w = f ( x , y , z) — это поверхности, определяемые уравнением f ( x , y , z) = k для значений k в диапазоне из ф . Пример. Диапазон функции w = f ( x , y , z) = x2 + 3y2 + 5z2 — это набор
Website: Math.byu.edu
Category : Использование в предложении
Функция, Для
Решите f (x + y) = f (x) + f (y) + 3xy Microsoft Math Solver
5 часов назад Если f не дифференцируем, мы все еще есть f (( x + y ) + z) = f (x + ( y + z)), откуда следует g ( xy ) + g (xz + yz) = g ( xy + xz) + g (yz) \ tag {1} Путем замены переменных x = \ sqrt {\ frac {ab} {c
Веб-сайт: Mathsolver.microsoft.com
Категория : Используйте слова в предложении
From, Follows, Frac
Максимумы и минимумы функций двух переменных
9 часов назад (0, 0), (1, 1 ) и (-1, -1) Теперь определим частные производные второго порядка. f xx ( x , y ) = 4 f yy ( x , y ) = 12y 2 f xy ( x , y ) = -4 Теперь мы используем таблица для изучения знаков D и f xx (a, b) и использования приведенной выше теоремы, чтобы решить, является ли данная критическая точка седловой точкой, относительным максимумом или минимумом.
Веб-сайт: Analyzemath.com
Категория : Используйте и в предложении
РЕШЕНИЯ UCSD Mathematics Home
1 час назад при условии ограничения 2×2 + ( y 1) 2 18: Решение : Проверяем на наличие критических точек в салоне fx = 2x; fy = 2 (y + 1) =) (0; 1) является критической точкой: Тест второй производной f …
Веб-сайт: Math.ucsd.edu
Категория : Используйте слова в предложении
Для
Выпуклые функции USM
2 часа назад f 2 ( x ; y ) = ln ( xy ) = lnx lny; для которого Hf 2 ( x ; y ) = x 2 0 0 y 2 также является положительным определением на Q 1.Следует отметить, что необходимо, чтобы только один из f 1 ( x ; y ) и f 2 ( x ; y ) был строго выпуклым, для f ( x ; y ) должно быть строго выпуклым, если обе функции хотя бы выпуклые. 2 Упражнения 1. Глава 2, Упражнение 1ac 2. Глава 2, Упражнение 2ad 3
Веб-сайт: Math.usm.edu
Категория : Используйте слова в предложении
For, Функции
Дифференцируемые функции нескольких переменных
1 час назад ∂2 f ∂x2 = (1 + xy ) (3y) + y 1 3xy) = 4y 6xy2 (16.10) ∂2 f ∂ y ∂ x = (1 + xy ) (3x) + x 1 3xy) = 4x 6x2y (16.11) ∂2 f ∂ x ∂ y = 4x (1 + xy ) + 2x2y 4x 6x2y (16.12) ∂2 f ∂y2 = 2×2 ( x ) 2×3: Обратите внимание, что вторая и третья строки равны. Это общий факт: смешанные части…
Веб-сайт: Math.utah.edu
Категория : Использование в предложении
Факт
В чем разница между y = f ( x) и y = f (x)? Quora
8 часов назад Ответ (1 из 14): y = f ( x ) обозначает любую заданную функцию. y = — f ( x ), следовательно, обозначает отрицательное значение функции, отрицательное значение всего f ( x ). Таким образом, это будет больше похоже на — ( f ( x )), если вы хотите, чтобы оно было более четким, точно так же, как письмо — y = f ( x ). Вы можете ясно видеть, что отрицательный результат находится на
Веб-сайт: Quora.com
Категория : Используйте разницу в предложении
Функция
Область функций $ f (x, y) = \ sqrt {x} \ sqrt {y} = \ sqrt {xy
2 часа назад Домен xy отличается от домена xy .Фактически, для первой функции. Показать активность в этом сообщении. для f ( x , y ) = x y , нам нужно x ≥ 0 и y ≥ 0, поэтому домен является первым квадрантом с двумя осями. для f ( x , y ) = x y , нам нужно x y ≥ 0, поэтому область является первым и третьим квадрантом с двумя осями.
Веб-сайт: Math.stackexchange.com
Категория : Использование в предложении
From, Fact, For, First, Function
Каковы экстремумы и седловые точки f (x , y) = 2x ^ 3
7 часов назад Следовательно, оцените Δ = f xxf yy — f 2 xy в каждой из этих точек.Определить характер экстремумов; Δ> 0 Существует минимум, если f xx <0 и максимум, если f yy> 0 Δ <0 существует седловая точка Δ = 0 Необходим дальнейший анализ. Итак, мы имеем: f (x, y ) = 2×3 + xy2 + 5×2 +…
Веб-сайт: Socratic.org
Категория : Использование и в предложении
Дальнейшее
Среднесрочные сроки экзамен 2, 7 апреля 2009 г. (решения)
8 часов назад Пусть f : R3 → R определяется как f ( x , y , z) = xy + exy + z2.Определите критическую точку (точки) f Определите критическую точку (точки) f и в каждой из них запишите квадратичное приближение.
Веб-сайт: Math.dartmouth.edu
Категория : Используйте слова в предложении
Найдите домен следующей функции: f (x, y) = ln (xy
7 часов назад Спасибо за ответ. Я определенно получаю ( x -1) y + x -1> 0. Как получить ( x -1) (y + 1)> 0.2 = 4 \ ,, \, z \ geq0 Это верхняя половина сферы радиуса 2 с центром в начале координат.
Веб-сайт: Quora.com
Категория : Использовать в предложении
Направленные производные Math
9 часов назад EX 1 Найдите производную по направлению от f ( x , y ) в точке (a, b) по направлению u. (Примечание: u может не быть единичным вектором.) A) f ( x , y ) = y2ln ( x ) (a, b) = (1,4) u = i — jb) f ( x , y ) = 2x2sin y + xy (a, b) = (1, π / 2) u = 2i + j…
Веб-сайт: Math.utah.edu
Категория : Используйте слова в предложении
Найдите
F (x, y) vs f (x, y, z) Форумы по физике
2 часа назад f (x, y ) — это функция в форматах x и y . Если вы нарисуете это в R 3, функция будет лежать в плоскости xy . Область действия функции — это плоскость x-y или какое-то ее подмножество. График функции — это упорядоченные тройки ( x , y , z), для которых z = f (x, y ).Пример: z = ln ( xy ). Домен — это часть плоскости, для которой xy > 0, которая является внутренней
Веб-сайт: Physicsforums.com
Категория : Используйте слова в предложении
Функция, для
DIFFYQS Slope fields
9 часов назад Интегрируйте, чтобы найти общее решение \ ( y = \ ln \, \ lvert x \ rvert + C \ text {.} \) Решение не существует в \ ( х = 0 \ текст {.} \) См. Рисунок 1.6. Уравнение могло быть записано как…
Веб-сайт: Jirka.org
Категория : Используйте слова в предложении
Найти, Рисунок
Примеры: Плотность суставов и функции совместной массы
1 час назад Пример 5: X и Y совместно непрерывны с соединенным pdf f ( x , y ) = (e− ( x + y ) если 0 ≤ x , 0 ≤ y 0, в противном случае.3
2 часа назад Сеть Stack Exchange состоит из 178 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Посетите Stack Exchange
Отзывов: 7
Веб-сайт: Math.stackexchange.com
Категория : Использование в предложении
Для
Рассмотрим показанный график. 2 — c).Он имеет следующие свойства: 1) График для f симметричен относительно оси y 2) График для f имеет вертикальную асимптоту при x = 2 3) график из f проходов. Математика. Каково уравнение…
Веб-сайт: Jiskha.com
Категория : Использование в предложении
Функция, после
УРОК 3 ГОРИЗОНТАЛЬНЫЙ И ВЕРТИКАЛЬНЫЙ СДВИГ Определение
6 часов назад 1.График для y c f ( x ) — это график для y f ( x ), сдвинутый на c единиц вверх. 2. График для y c f ( x ) — это график для y f ( x ), сдвинутый на c единиц вниз. Чтобы определить величину и направление вертикального сдвига, коэффициент переменной y должен быть равен единице. Пример На графике функция h задана как 5 2 1 h ( x ) x2.
Веб-сайт: Math.utoledo.edu
Категория : Используйте слова в предложении
Функция
Построение графиков — Учебник Sage v9.4
Sage может создавать двумерные и трехмерные изображения сюжеты.
Двумерные графики
В двух измерениях Sage может рисовать круги, линии и многоугольники; графики функций в прямоугольных координатах; а также полярные графики, контурные графики и графики векторных полей.Мы представляем примеры некоторые из них здесь. Дополнительные примеры построения графиков с помощью Sage см. Решение дифференциальных уравнений и максимумов, а также Конструкции Мудреца документация.
Эта команда создает желтый круг радиуса 1 с центром в происхождение:
мудрец: круг ((0,0), 1, rgbcolor = (1,1,0)) Графический объект, состоящий из 1 графического примитива
Вы также можете создать закрашенный круг:
sage: circle ((0,0), 1, rgbcolor = (1,1,0), fill = True) Графический объект, состоящий из 1 графического примитива
Вы также можете создать круг, присвоив его переменной; это не рисует:
мудрец: c = круг ((0,0), 1, rgbcolor = (1,1,0))
Для построения используйте c.show () или show (c) , как показано ниже:
В качестве альтернативы, оценка c.save ('filename.png') сохранит
сюжет в данный файл.
Теперь эти «круги» больше похожи на эллипсы, потому что оси масштабируется иначе. Вы можете исправить это:
мудрец: c.show (aspect_ratio = 1)
Команда show (c, aspect_ratio = 1) выполняет то же самое.
вещь, или вы можете сохранить изображение, используя c.save ('filename.png', Aspect_ratio = 1) .3), (x, 0,2 * pi), rgbcolor = hue (0,6))
мудрец: показать (p1 + p2 + p3, axes = false)
Хороший способ создания форм с заливкой — создание списка
точек ( L в примере ниже), а затем используйте полигон команда для построения фигуры с границей, образованной этими точками. Для
Например, вот зеленая дельтовидная мышца:
мудрец: L = [[-1 + cos (pi * i / 100) * (1 + cos (pi * i / 100)), ....: 2 * sin (pi * i / 100) * (1-cos (pi * i / 100))] для i в диапазоне (200)] мудрец: p = многоугольник (L, rgbcolor = (1 / 8,3 / 4,1 / 2)) шалфей: p Графический объект, состоящий из 1 графического примитива
Введите show (p, axes = false) , чтобы увидеть это без каких-либо осей.
К сюжету можно добавить текст:
мудрец: L = [[6 * cos (pi * i / 100) + 5 * cos ((6/2) * pi * i / 100),
....: 6 * sin (pi * i / 100) -5 * sin ((6/2) * pi * i / 100)] для i в диапазоне (200)]
мудрец: p = многоугольник (L, rgbcolor = (1 / 8,1 / 4,1 / 2))
sage: t = text ("гипотрохоид", (5,4), rgbcolor = (1,0,0))
шалфей: показать (п + т)
Учителя математического анализа часто рисуют на доске следующий график: не одна ветвь arcsin, а несколько из них: т.е. график \ (y = \ sin (x) \) для \ (x \) между \ (- 2 \ pi \) и \ (2 \ pi \), перевернутый относительно линии под углом 45 градусов.Следующий Команды мудреца составляют это:
sage: v = [(sin (x), x) for x in srange (-2 * float (pi), 2 * float (pi), 0.1)] мудрец: линия (v) Графический объект, состоящий из 1 графического примитива
Поскольку функция тангенса имеет больший диапазон, чем синус, если вы используете тот же трюк, чтобы построить арктангенс, вы должны изменить минимальные и максимальные координаты для оси x :
sage: v = [(tan (x), x) для x в srange (-2 * float (pi), 2 * float (pi), 0,01)] sage: show (строка (v), xmin = -20, xmax = 20)
Sage также вычисляет полярные диаграммы, контурные диаграммы и графики векторных полей. 2, (x, -2,2), (y, -2,2)) Объект Graphics3d
В качестве альтернативы вы можете использовать Parameter_plot3d для построения графика
параметрическая поверхность, где каждое из \ (x, y, z \) определяется
функция одной или двух переменных (параметры, обычно
\ (и \) и \ (v \)).2
мудрец: параметрический_плот3d ([fx, fy, fz], (u, -1, 1), (v, -1, 1),
….: frame = False, color = «yellow»)
Объект Graphics3d
Крестовина:
мудрец: u, v = var ('u, v')
мудрец: fx = (1 + cos (v)) * cos (u)
мудрец: fy = (1 + cos (v)) * sin (u)
мудрец: fz = -tanh ((2/3) * (u-pi)) * sin (v)
sage: параметрический_plot3d ([fx, fy, fz], (u, 0, 2 * pi), (v, 0, 2 * pi),
....: frame = False, color = "red")
Объект Graphics3d
Скрученный тор:
мудрец: u, v = var ('u, v')
мудрец: fx = (3 + sin (v) + cos (u)) * cos (2 * v)
мудрец: fy = (3 + sin (v) + cos (u)) * sin (2 * v)
мудрец: fz = sin (u) + 2 * cos (v)
мудрец: параметрический_плот3d ([fx, fy, fz], (u, 0, 2 * pi), (v, 0, 2 * pi),
.


 title(name)
title(name)
 Щелкните заголовок Level … , чтобы открыть диалоговое окно Set Levels , чтобы установить Minor Levels как 4 .
Щелкните заголовок Level … , чтобы открыть диалоговое окно Set Levels , чтобы установить Minor Levels как 4 . Д.
Д.
 Нет значений или комбинаций xx и yy, которые заставляют f (x, y) f (x, y) быть неопределенным, поэтому область определения ff равна ℝ2.ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно такое решение может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ.
Нет значений или комбинаций xx и yy, которые заставляют f (x, y) f (x, y) быть неопределенным, поэтому область определения ff равна ℝ2.ℝ2. Чтобы определить диапазон, сначала выберите значение для z.z. Нам нужно найти решение уравнения f (x, y) = z, f (x, y) = z или 3x − 5y + 2 = z.3x − 5y + 2 = z. Одно такое решение может быть получено, если сначала задать y = 0, y = 0, что дает уравнение 3x + 2 = z.3x + 2 = z. Решением этого уравнения является x = z − 23, x = z − 23, что дает упорядоченную пару (z − 23,0) (z − 23,0) как решение уравнения f (x, y) = zf (x, y) = z для любого значения z.z. Следовательно, диапазон функции — это все действительные числа или ℝ.ℝ. Область включает граничный круг, как показано на следующем графике.
Область включает граничный круг, как показано на следующем графике. 9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.
9 − x2 − y2 = c9 − x2 − y2 = c2x2 + y2 = 9 − c2.  1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
1, мы определили, что область определения g (x, y) = 9 − x2 − y2g (x, y) = 9 − x2 − y2 равна {(x, y) ∈ℝ2 | x2 + y2≤9} {(x , y) ∈ℝ2 | x2 + y2≤9}, а диапазон равен {z∈ℝ2 | 0≤z≤3}. {z∈ℝ2 | 0≤z≤3}. Когда x2 + y2 = 9×2 + y2 = 9, мы имеем g (x, y) = 0. G (x, y) = 0. Следовательно, любая точка на окружности радиуса 33 с центром в начале координат в x, y-planex, y-плоскости отображается в z = 0z = 0 в ℝ3.ℝ3. Если x2 + y2 = 8, x2 + y2 = 8, то g (x, y) = 1, g (x, y) = 1, поэтому любая точка на окружности радиуса 2222 с центром в начале координат x, y -planex, y-плоскость отображается в z = 1z = 1 в ℝ3.ℝ3. Когда x2 + y2x2 + y2 приближается к нулю, значение z приближается к 3.Когда x2 + y2 = 0, x2 + y2 = 0, тогда g (x, y) = 3.g (x, y) = 3. Это начало координат в плоскости x, y, плоскости x, y. Если x2 + y2x2 + y2 равно любому другому значению между 0 и 9,0 и 9, то g (x, y) g (x, y) равно некоторой другой константе между 0 и 3,0 и 3. Поверхность, описываемая этой функцией, представляет собой полусферу с центром в начале координат с радиусом 33, как показано на следующем графике.
Ваш комментарий будет первым