Y от x: Построение графиков функций онлайн

График функции y=kf(x) | Алгебра

График функции y=kf(x) (k>1) можно получить из графика функции y=f(x) растяжением от оси Ox в k раз. При таком преобразовании каждая точка (x; y) графика функции y=f(x) переходит в точку (x; ky) графика функции y=kf(x):

(x; y) → (x; ky)

(то есть абсцисса (x) каждой точки начального графика остаётся без изменений, а ордината (y) увеличивается в k раз).

При растяжении от оси Ox точки графика y=f(x), лежащие на оси абсцисс, остаются на месте, так как k∙0=0.

Примеры.

1) График функции y=3x² получен из графика функции y=x² растяжением в 3 раза от оси Ox.

При растяжении графика от оси абсцисс нужно ординату каждой точки увеличить в 3 раза.

Для построения графика отмечаем базовые точки графика y=x². Для каждой точки координату x оставляем неизменной, значение координаты y умножаем на 3. Таким образом, каждая точка нового графика располагается строго над соответствующей точкой графика y=x²,  в 3 раза дальше от оси Ox.

Вершина параболы y=x², точка O (0; 0), остаётся на месте (так как 3∙0=0).

График y=3x² из y=x²

 

  (1; 1) → (1; 3),

  (-1; 1) → (-1; 3),

  (2; 4) → (2; 12),

  (-2; 4) → (-2; 12)

и т. д.

 

 

2) График функции y=2|х| можно получить из графика функции y=|х| растяжением от оси абсцисс в 2 раза.

Точка O (0; 0) остаётся на месте. В I и II координатных четвертях берём по одной точке графика y=|х|, например, (5; 5) и (-5; 5). Их абсциссы оставляем без изменений, а ординаты удваиваем:

График y=2|х| из y=|х|

   (5; 5)→ (5; 10),

   (-5; 5)→ (-5; 10).

Через эти точки из точки O проводим лучи.

Получаем график функции y=2|х|

 

 

 

 

3) График функции y=4√x можно получить из графика функции y=√x растяжением от оси Ox в 4 раза.

Координату x каждой из базовых точек графика y=√x оставляем без изменений, координату y увеличиваем в 4 раза. Точка O (0; 0) при этом остаётся на месте.

Через полученные точки проводим новый график:

График y=4√x из y=√x

 

(0; 0) → (0; 0),

(1; 1) → (1; 4),

(4; 2) → (4; 8),

(9; 3) → (9; 12),

и т. д.

 

 

 

Преобразование графиков может быть использовано для построения графиков функций в ходе решения примеров из разных разделов алгебры.

2.Квадратичная функция y=x² — Функции и их графики

В уравнении квадратичной функции:

a – старший коэффициент

b – второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

 Точки, обозначенные зелеными кружками – это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.

График  функции  имеет вид:

Для нахождения координат базовых точек составим таблицу:

 

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение .

В процессе решения квадратного уравнения находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

2. Если ,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

3.  Если ,то уравнение  имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следующий важный параметр графика квадратичной функции – координаты вершины параболы:

 

Прямая, прохдящая через вершину параболы параллельно оси OY является осью симметрии паработы.

И еще один параметр, полезный при построении графика функции – точка пересечения параболы  с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: . 2

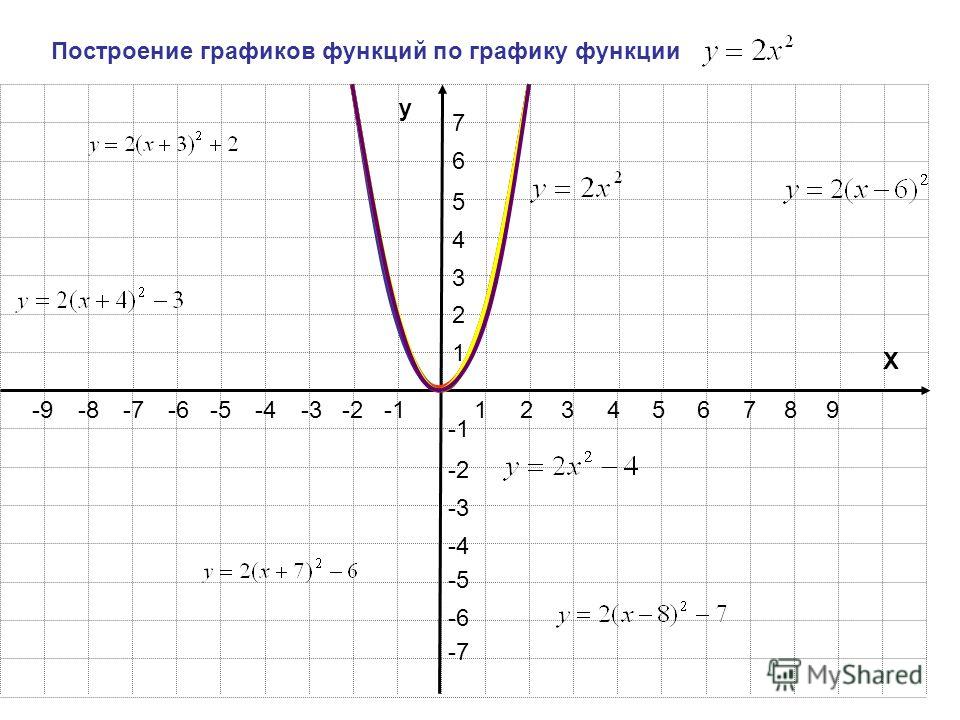
Найдём связь между графиками функций  и .

Для этого изобразим в одной координатной плоскости графики функций , , .

Составим таблицы значений для функций:

Видно, что график функции  можно получить из графика  в квадрате параллельным переносом относительно оси х вправо на 6 единиц, m=6. А график функции  параллельным переносом влево на 6 единиц, m=-6.

Определение:

График функции  является параболой, которую можно получить из графика функции  с помощью параллельного переноса вдоль оси х на m единиц вправо, если m>0, и на —m единиц влево, если m<0.

Пример.

Изобразить графики функций вида , пользуясь уже известными определениями.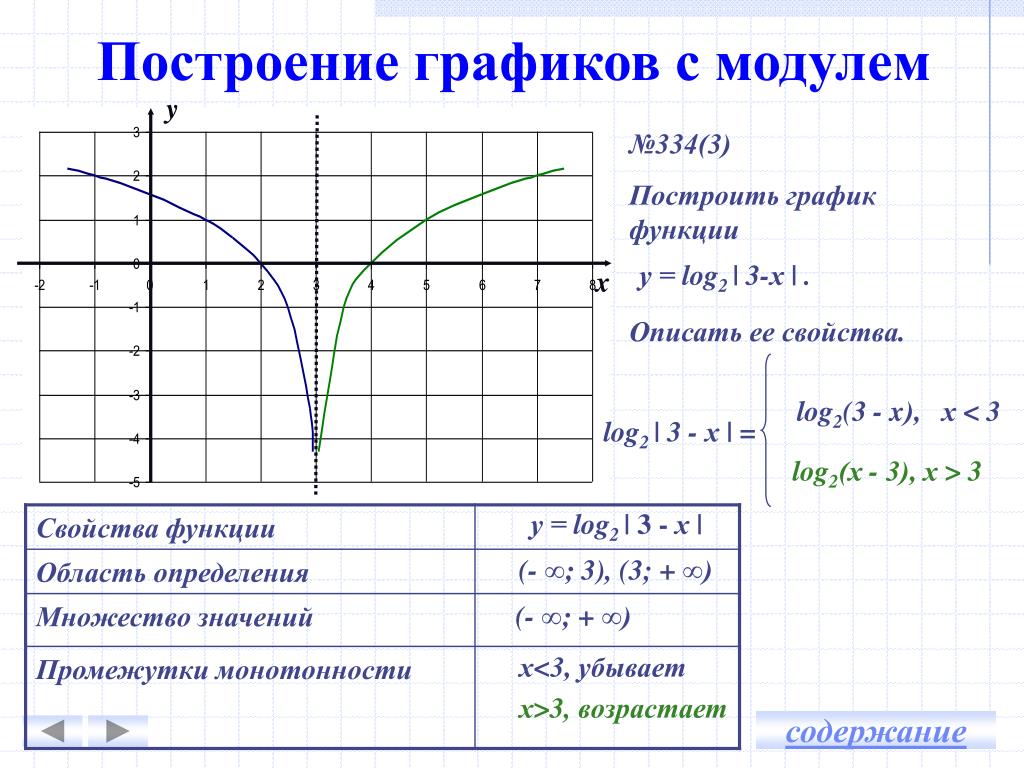

Используя шаблон , изобразим графики функции .

Сначала рассмотрим шаблон. Не трудно составить таблицу значений этой функции:

Получаем параболу.

Взглянем на формулу, которой задана функция . Это функция вида , в данном случае m=-4. Получить график этой функции можно с помощью параллельного переноса параболы  относительно оси х на 4 единицы влево.

Получили график функции . Вершина данной параболы имеет координаты (-4,0).

Заметим, что вершина параболы  будет иметь координаты (m,0).

Определение:

Функция вида  – это парабола, которую можно получить из графика функции  в квадрате с помощью двух параллельных переносов:

1.     вдоль оси y на n единиц вверх, если n>0, и на —n единиц вниз, если n<0;

2.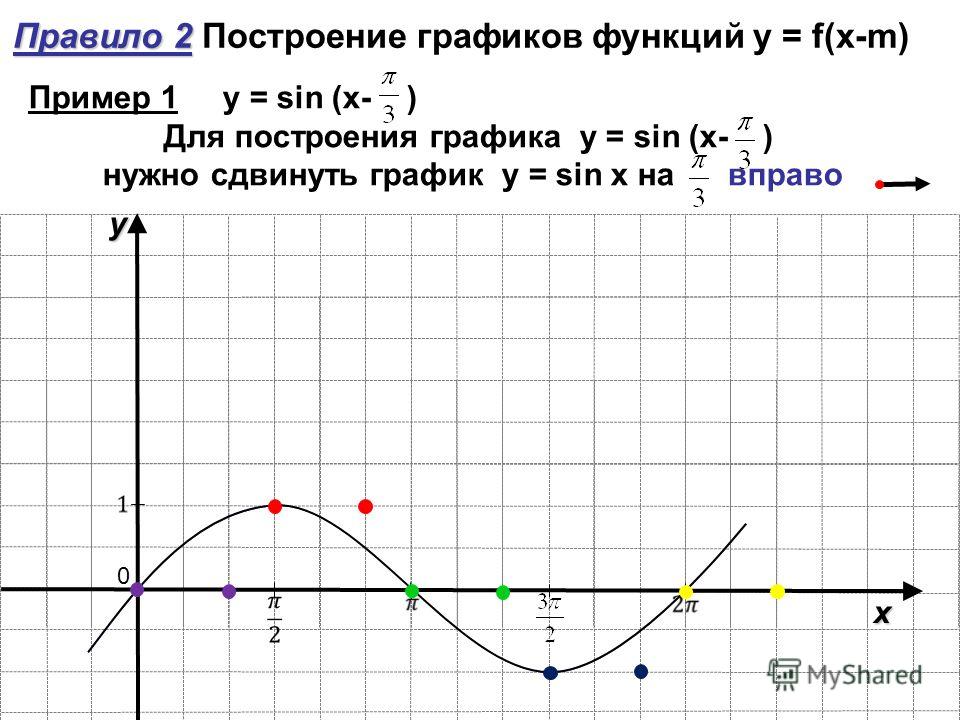      вдоль оси x на m единиц вправо, если m

>0, и на —m единиц влево, если m<0.

Параллельные переносы можно производить в любом порядке.

Вершина этой параболы будет иметь координаты (m,n).

Пример.

С помощью шаблона параболы  изобразить график функции .

На рисунке видно, что m=-4, сдвигаем точки шаблона на 4 единицы влево и n=-3, сдвигаем полученный график на 3 единицы вниз. Получили график функции . Вершина имеет координаты (-4,-3).

заказ решений на аукционе за минимальную цену с максимальным качеством

Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:

• решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
• написание лабораторных, рефератов и курсовых
• выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.

Объединение сервисов в одну систему

Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:

• Форум, где посетители обмениваются идеями и помогают друг другу
• Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
• Аукцион, где цена за товар или услугу определяется в результате торгов
• Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос

Принцип работы

Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.

Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.

Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.

Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.

к. можно учитывать и другие факторы – см. выше).

Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.

За счет чего будет развиваться сервис

Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.

Второе – удобный сервис для заказчиков и для желающих заработать на решениях.

Преимущества для заказчиков

Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.

Преимущества для решающих задания

Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.

Преимущества для владельца сервиса

Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.

Что необходимо для создания сервиса

1. Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.

   Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

2. Выбрать платежную систему.
3. Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
4. Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.

Степенная функция, ее свойства и график

Вы знакомы с функциями y=x, y=x², y=x³, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=x^p, где p — заданное действительное число.
Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень x^p. Перейдем к подобному рассмотрению различных случаев в зависимости от
показателя степени p.

1. Показатель p=2n -четное натуральное число.

В этом случае степенная функция y=x²ⁿ, где n — натуральное число, обладает следующими

свойствами:

• область определения — все действительные числа, т. е. множество R;
• множество значений — неотрицательные числа, т. е. y больше или равно 0;
• функция y=x²ⁿ  четная, так как x²ⁿ=(-x)²ⁿ
• функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.

График функции y=x²ⁿ имеет такой же вид, как например график функции y=x⁴.

        2. Показатель p=2n-1— нечетное натуральное число
В этом случае степенная функция  y=x^2n-1 , где натуральное число, обладает следующими свойствами:

• область определения — множество R;
• множество значений — множество R;
• функция y=x^2n-1 нечетная, так как (-x)^2n-1=x^2n-1;
• функция является возрастающей на всей действительной оси.

График функции y=x^2n-1 имеет такой же вид, как, например, график функции y=x³.

       3.Показатель p=-2n, где n — натуральное число.

В этом случае степенная функция y=x^-2n=1/x²ⁿобладает следующими свойствами:

• область определения — множество R, кроме x=0;
• множество значений — положительные числа y>0;
• функция  y=1/x²ⁿ четная, так как 1/(-x)²ⁿ=1/x²ⁿ;
• функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.

График функции y=1/x²ⁿ имеет такой же вид, как, например, график функции y=1/x².
       4.Показатель p=-(2n-1), где n — натуральное число.
В этом случае степенная функция y=x^-(2n-1) обладает следующими свойствами:

• область определения — множество R, кроме x=0;
• множество значений — множество R, кроме y=0;
• функция y=x^-(2n-1) нечетная, так как (-x)^-(2n-1) =-x^-(2n-1);
• функция является убывающей на промежутках x<0 и x>0.

График функции y=x^-(2n-1) имеет такой же вид, как, например, график функции y=1/x³.

Область определения функции y(x)

Областью определения называют множество значений аргумента при котором существует значение функции и обозначают или . Областью значений называют множество чисел, которые принимает функция при прохождении аргументом всех значений из области определения.
Ее обозначают или . Графически обе области хорошо иллюстрирует следующий рисунок

Для схематической функции рассматриваемые области принимают значения

Методика нахождения области определения для всех функций одна и та же: нужно выявить точки при которых функция не существует, а затем исключить из множества действительных чисел . В результаты получим набор промежутков или интервалов, точки, которые образуют область определения.

Особенности элементарных функций

1) Если функция имеет вид полинома то ее областью определения будет вся действительная ось или . Такая функция определена повсюду.

2) Дробно рациональная функция , где – полиномы, областью определения имеет значения аргумента при которых знаменатель не превращается в ноль. Сначала находим решения уравнения, если те существуют, вырезаем из множества действительных значений. В результате получим набор интервалов

где – корни уравнения .

3) Функция содержит корень парного степени . В таком случае областью определения будут точки , при которых подкоренная функция принимает неотрицательные значения, т.е. решения неравенства .

4) Если корень содержит знаменатель

то область определения определяют из строгого неравенства .

5) Если в знаменателе имеем корень нечетной степени

то область определения находим из условия .

5) Если является логарифмом от другой функции , то по свойству логарифма область определения находим из условия . Как правило, это будет интервал или несколько интервалов.

6) Экспонента областью определения имеет множество аргументов , для которых определена . Например, функция определена на всей действительной оси.

7) Простые тригонометрические функции (косинус и синус) определены на всем множестве действительных чисел .

8) Тангенс и котангенс областями определения имеют интервалы, граничащих между собой точками

для первой функции и

для второй, т.е.

В случаях когда при аргументах есть множители , точки в которых функция не существует следует определять из условия

Подобным образом и для котангенса

9) Следует отметить, что обратные тригонометрические функции — арксинус и арккосинус областями значений имеют отрезок . Для отыскания областей определения необходимо решить двойное неравенство

Например, для функции имеем неравенство с которого получим

При суперпозиции функций, то есть когда задана их комбинацию, нужно находить область определения каждой из функций, после чего — сечение найденных областей.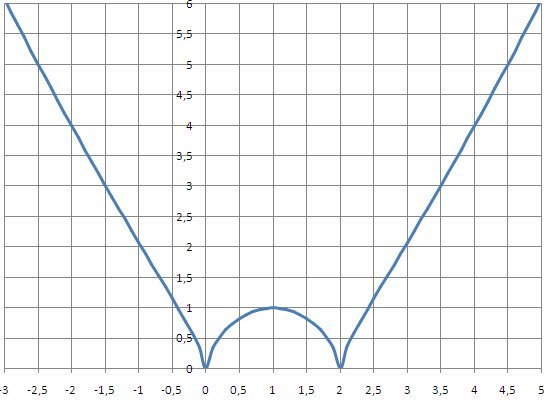

Пример.

Решение.

Область определения первого слагаемого находим из неравенства

Второй и третий дадут следующий вклад

Сечением найденных областей будет интервал

—————————————

Находите области определения по приведенной выше схеме, выключайте все лишние промежутки и точки и не допускайте ошибок. Помните, что установление областей определения — это одно из самых простых заданий при исследовании функции.

Посмотреть материалы:

Яка точка перетину осі x і y у системі координат? — Математика

Осі x і y є частиною декартової системи координат, яку також називають прямокутною системою координат. Координати в цій системі розташовані на їх відстані від перпендикулярних прямих (осі x і y), які перетинаються. Кожну лінію, фігуру і точку геометрії координат можна намалювати в координатній площині за допомогою декартової системи координат.

Походження декартової системи координат

Рене Декарт, французький філософ і математик, винайшов декартову систему координат. У 1637 р. Він опублікував книгу «Дискурс про спосіб розумувати розум і шукати правду в науках», що включала розділ під назвою «La Géometrie» або Геометрія. У цьому розділі Декарт вперше описав декартову систему координат, поєднавши геометрію та алгебру.

Як працює система координат

Декартова система координат складається з двох числових ліній, однієї горизонтальної та однієї вертикальної. Горизонтальна лінія відома як вісь x, а вертикальна називається віссю y. Ці осі перетинаються, утворюючи чотири квадранти. Оскільки осі x і y перпендикулярні одна одній, вони перетинаються лише один раз, у місці, яке називається початком. Координати вимірюються заданою довжиною, яка дорівнює відстані від початку.

Як описати координати перетину осі X та Y

Координати записуються як (x, y), де x означає значення на осі x (горизонталь), а y означає значення на осі y (вертикаль). Місце, де зустрічаються вісь x і вісь y, дорівнює нульовому значенню як по осях x, так і y. Оскільки осі x і y обидва перетинаються в нулі, координата точки їх перетину описується як (0, 0).

Як описати інші координати

Точка, розташована у квадранті I, у верхньому правому куті, має додатне значення координат x та y, наприклад (1, 1). Точка, розташована у квадранті II у верхній лівій частині, має від’ємне значення x та позитивне y, наприклад (-1, 1). Точка в квадранті III, у лівій нижній частині, має від’ємне значення координат x і y, наприклад: (-1, -1). Точка у квадранті IV у правій нижній частині має позитивне значення x та від’ємну y координату, наприклад (1, -1).

Узнайте об отражении над линией Y = X

Из этого видео вы узнаете, как сделать отражение по линии y = x .

Линия y = x при построении графика на графическом калькуляторе будет выглядеть как прямая линия, пересекающая начало координат с наклоном 1 .

При отражении координатных точек прообраза по линии для определения координатных точек изображения могут использоваться следующие обозначения:
r _{y = x} = (y, x)

Например, :

Для треугольника ABC с координатными точками A (3,3), B (2,1) и C (6,2) примените отражение по линии y = x.

Следуя обозначениям, мы поменяем местами значение x и значение y.
A (3,3), B (2,1) и C (6,2) превратятся в
A ‘(3,3), B’ (1,2) и C ‘(2,6)

Стенограмма видеоурока

В этом уроке мы рассмотрим отражение над линией.

Прежде всего, что такое линия?

Это строка, в которой для каждого значения мы получаем одно и то же значение.

будет выглядеть примерно так. Диагональная прямая.

Когда,.Когда , . И когда , . И так далее.

Если у нас есть точка зрения, например, мы собираемся ее продумать. Нам нужно двигаться перпендикулярно ему.

Одна сторона должна быть перпендикулярна другой стороне.

Наше изображение сейчас.

Все, что мы сделали, это поменяли местами значения и.

Например, если исходное изображение.

Нам нужно провести перпендикулярную линию, чтобы измерить расстояние. Затем сделайте такое же расстояние до другой стороны.

Отраженная точка есть.

Когда мы отражаемся над линией, мы просто меняем значения и.

Давайте посмотрим на пример, где мы отразим треугольник ABC над линией, используя координаты.

Мы знаем, что по правилу координаты будут переключаться на. Мы просто поменяем их местами.

Давайте теперь изобразим это на графике. И нарисуйте треугольник.

Теперь у нас есть отражение треугольника над линией, на которой формируется изображение.

График X и Y — Определение, различия, уравнения на графике X и Y, примеры

Графики x и y, также известные как оси x и y, представляют собой две важные линии, составляющие график.График состоит из горизонтальной оси и вертикальной оси, на которой могут быть представлены данные.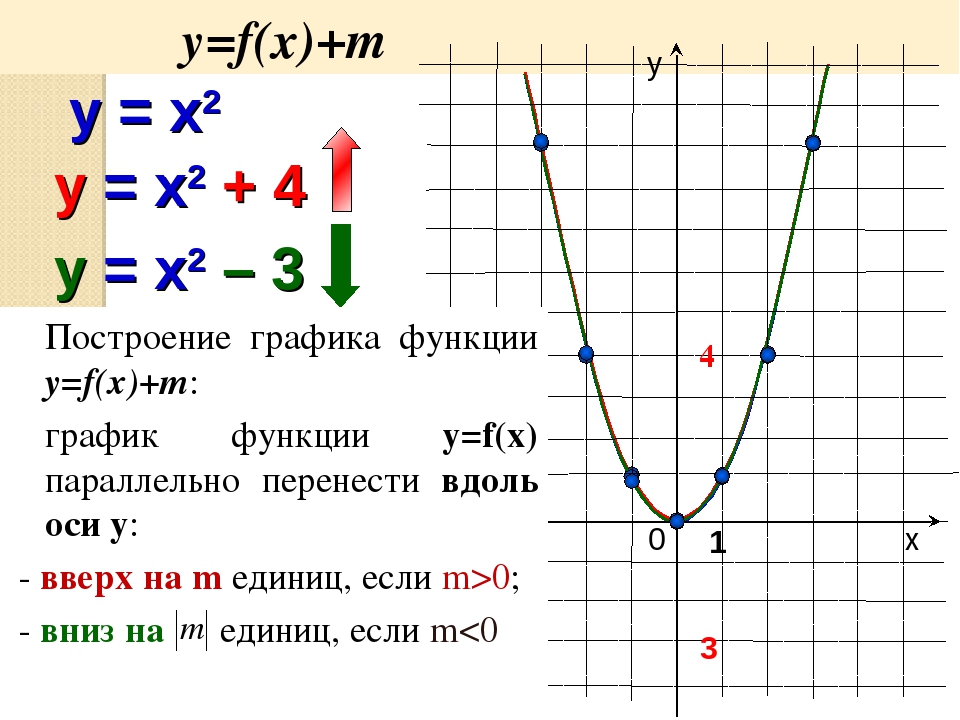 Точку можно описать горизонтально или вертикально, что легко понять с помощью графика. Эти горизонтальные и вертикальные линии или оси на графике являются осью x и осью y соответственно. Давайте узнаем больше о графике x и y в математике, таблице, диаграммах и решим несколько примеров, чтобы лучше понять концепцию.

Определение графиков X и Y

Графики x и y могут быть определены по двум осям i.е. Ось x и ось y, которые образуют координатную плоскость для графика. Горизонтальная ось представлена ​​осью x, а вертикальная ось представлена ​​осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. На изображении ниже представлена ​​координатная плоскость с обеими осями.

Ось X на графике также известна как абсцисса. Ось Y на графике также называется ординатой. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (x-координата, y-координата) или (x, y), где x-координата представляет точку на оси x или перпендикуляре. расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x.Граф x и y имеет 4 квадранта, т.е. каждая перпендикулярная линия представляет собой один квадрант. На изображении ниже изображены графики x и y как с положительными, так и с отрицательными координатами.

Например: Население города с 2015 по 2020 год указано в таблице графиков X и Y как:

Годы	2015	2016	2017	2018	2019	2020
Люди в миллионах	1	1.5	2	2,5	3	3,5

Чтобы найти любую точку на координатной плоскости, мы используем упорядоченную пару, в которой упорядоченная пара записывается как (x-координата, y-координата) или (x, y), где x-координата представляет точку на Ось x или перпендикулярное расстояние от оси y, а координата y представляет точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найдите точку.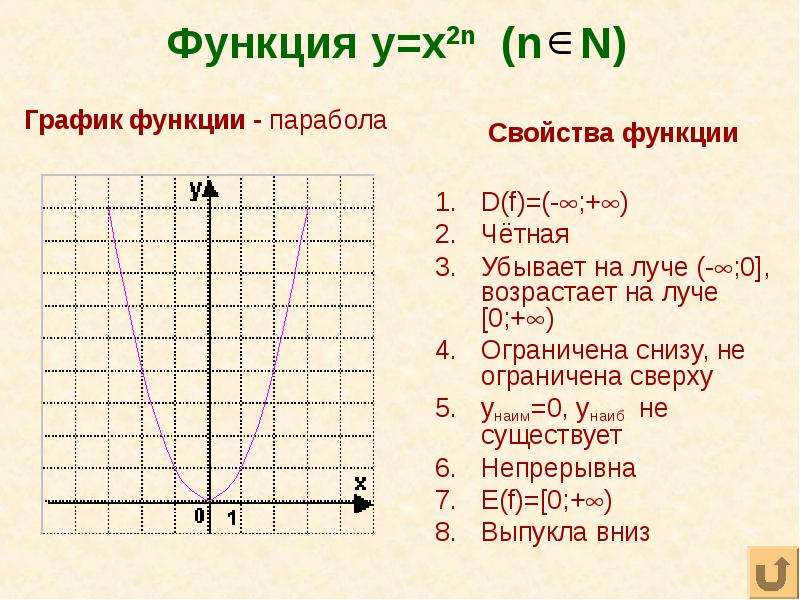 Мы можем видеть здесь, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x ведет к оси y или координате y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующую численность населения на оси y как:

Разница между графиками осей X и Y

График x и y состоит из оси x и оси y, которые образуют координатную плоскость графика, где числа представлены для сравнения или даже формирования линейных уравнений.Есть много различий между осью x и осью y, даже если у них одна и та же исходная точка. Посмотрим на отличия:

Ось x графика	Ось Y графика
Это горизонтальная плоскость графика в декартовой системе координат, которая дает числовое значение в каждой точке.	Это вертикальная плоскость графика в декартовой системе координат, которая дает числовое значение в каждой точке.
Ось x называется абсциссой.	Ось Y называется ординатой.
Переменные на оси x представляют причину данных.	Переменные на оси Y представляют следствие причины данных.
Числа, расположенные на оси x, называются координатами x.	Числа, расположенные на оси y, называются координатами y.
Ось x представляет собой горизонтальную линию с 0 в качестве начала координат, положительными числами справа и отрицательными числами слева.	Ось Y проводится вертикально снизу вверх с тем же началом, что и ось X, с положительными числами вверху и отрицательными числами внизу.
Координаты, относящиеся к оси x, записываются как (x, y).	Координаты, относящиеся к оси y, записываются как (y, x).

Построение уравнения по осям X и Y

На графике x и y можно изобразить линейное уравнение, показывающее координаты как оси x, так и оси y.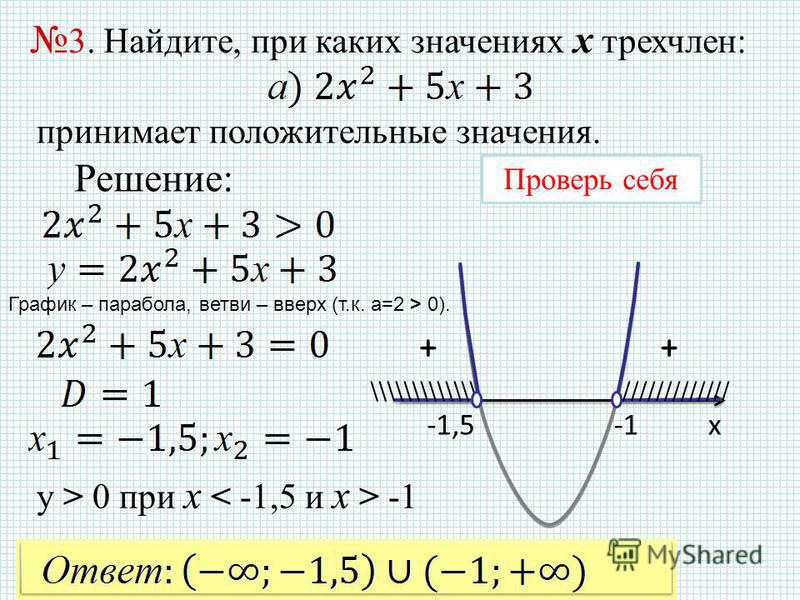 В геометрии линейное уравнение можно изобразить с помощью графиков x и y, и они будут представлены в виде прямой линии. Давайте посмотрим на пример, чтобы лучше понять это:

Давайте рассмотрим линейное уравнение y = 2x + 1. Теперь, чтобы построить график этого уравнения, постройте таблицу, имеющую два столбца для значений x и y. Выберем несколько значений переменной x и найдем соответствующие значения для y. Если x = 1, то y = 2 × 1 + 1 = 3. Если x = 2, то y = 2 × 2 + 1 = 5 и сын дальше. Здесь мы берем значения всего трех точек, начиная с 0.Чтобы нарисовать график координат осей x и y линейного уравнения, нам нужно нарисовать таблицу сетки осей x и y как минимум для двух точек.

Теперь нарисуйте точки на графике, где значения x лежат на оси x, а соответствующие значения y лежат на оси y. Затем соедините точки прямой линией, чтобы нарисовать график уравнения.

Уравнение оси Y

Ось Y — это линия, на которой значения координаты x равны нулю для всех значений y. Тогда точки данных для оси Y: (0, -1), (0, 0,5), (0, 1), (0, 1,5). Следовательно, уравнение оси Y — x = 0, и его график на диаграмме x и y показан ниже. Если мы подставим значение x как 0 в общее уравнение y = mx + c, мы сможем найти координаты для y.

Уравнение оси X

Ось X — это линия, на которой значения координаты y равны нулю для всех значений x. Тогда точки данных для оси x: (1,0), (-1.5, 0) Следовательно, уравнение оси x имеет вид y = 0, и его график на диаграмме x и y показан ниже. Если мы подставим значение y как 0 в общее уравнение y = mx + c, мы сможем найти координаты для x.

Связанные темы

Ниже перечислены несколько интересных тем, связанных с графиками x и y, взгляните.

Часто задаваемые вопросы о графике X и Y

Что такое график X и Y?

График x и y — это визуальное представление данных, которое отображается в виде графика с осью x и осью y, которые образуют координатные плоскости.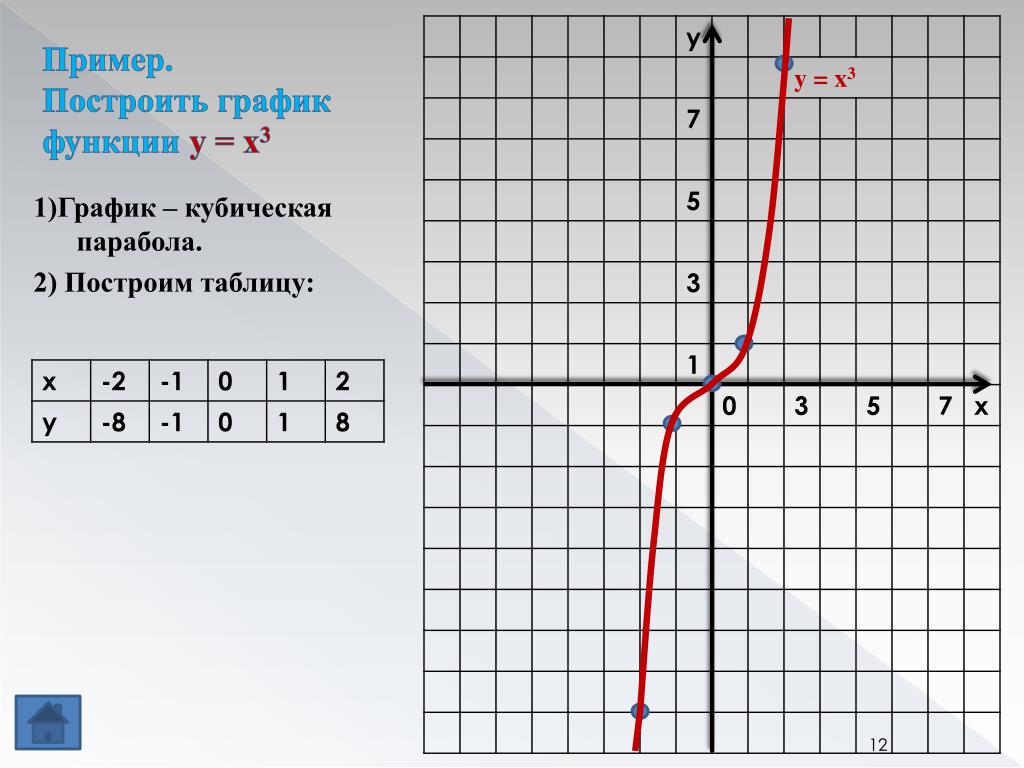 Ось X на графике также известна как абсцисса, тогда как ось Y известна как ордината. Любая точка на координатной плоскости хорошо определяется упорядоченной парой, где упорядоченная пара записывается как (x-координата, y-координата) или (x, y), где x-координата представляет точку на оси x или перпендикуляре. расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x. Граф x и y имеет 4 квадранта.

Как построить уравнение на графике X и Y?

Для построения графика уравнения сначала постройте таблицу, содержащую два столбца для значений x и y, подставив значения x и y в уравнение, начиная с 0.Затем нарисуйте точки на графике, где значения x лежат на оси x, а соответствующие значения y лежат на оси y. Затем соедините точки, чтобы нарисовать график уравнения. Обычно это прямая линия, которая может быть диагональной, вертикальной или горизонтальной при построении линейного уравнения.

Какая точка находится на отрицательной оси Y на графиках X и Y?

Точка с отрицательным значением координаты y находится на отрицательной оси y. Поскольку ось Y — это вертикальная линия, которая начинается снизу вверх, отрицательные числа лежат в нижней части области и покрывают 3-й и 4-й квадранты графика.

Какая ось X и какая ось Y на графике X и Y?

Горизонтальная ось называется осью x, а вертикальная ось — осью y. Начало 0 является общим множителем для обеих осей. Ось X показывает причину данных, а ось Y показывает влияние данных. Например, при отображении температуры в Нью-Йорке ось абсцисс показывает недели, а ось ординат — температуру. Каждая точка на обеих осях будет показывать предыдущее значение, начиная с 0.

Как построить график с осями X и Y?

Сначала мы рисуем и маркируем оси x и y. Затем мы наносим на график координаты функции при различных значениях координат x и y. Затем мы соединяем координаты и строим график функции.

Как называются оси X и Y на графиках X и Y?

Вертикальная ось, то есть ось Y, называется осью абсцисс. А ось x известна как ось ординат. x

Возьмите калькулятор.x, чтобы облегчить нашу жизнь.

Шаг 1. Первое, что вам нужно сделать, это включить калькулятор. Ага!

Шаг 2. Затем убедитесь, что на экране (дисплее) нет никаких цифр. Иногда калькулятор включается и удерживает число, если вы не очистили экран перед его выключением. Где-то должна быть четкая клавиша (C), поэтому просто нажмите ее, если нужно.

Шаг 3. Теперь, когда на экране нет чисел, введите 10 в калькулятор.x, затем введите показатель степени и после этого нажмите знак равенства, чтобы получить ответ!

Решить y = x-9 Решатель алгебры тигра

Решить y = x-9 Решатель алгебры тигра

Этот сайт лучше всего просматривать с помощью Javascript. Если вы не можете включить Javascript, нажмите здесь.

Вход камеры не распознается!

Мы думаем, что вы написали:

y = x-9

Это касается свойств прямой линии.

yi «ntercept = -9 / 1 = -9.00000

Пошаговое решение

Переставить:

Переставить уравнение, вычтя то, что находится справа от знака равенства, из обеих частей уравнения:

y- (x-9) = 0

Шаг 1:

 
 Уравнение прямой 
 
 1. 1 Решите y-x + 9 = 0 
 
 Тигр понимает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании). 
 
 «y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось. 
 
 В этой формуле: 
 
 y сообщает нам, как далеко идет линия. 
 x сообщает нам, как далеко вдоль 
 м находится наклон или градиент, т.е. насколько крутой является линия. 
 b является пересечением по оси Y i.е. где линия пересекает ось Y 
 
 Пересечения X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-x + 9 = 0 и вычислим ее свойства 
 
 График прямой линии: 
 
 
 Вычислите точку пересечения оси Y: 
 Обратите внимание, что при x = 0 значение y равно -9 / 1, поэтому эта линия «срезает» ось y в точке y = -9,00000
 пересечение оси y = -9/1 = -9,00000 
 Вычислить пересечение оси X: 
 При y = 0 значение x равно 9 / 1 Наша линия, таким образом, «разрезает» ось x в точке x = 9.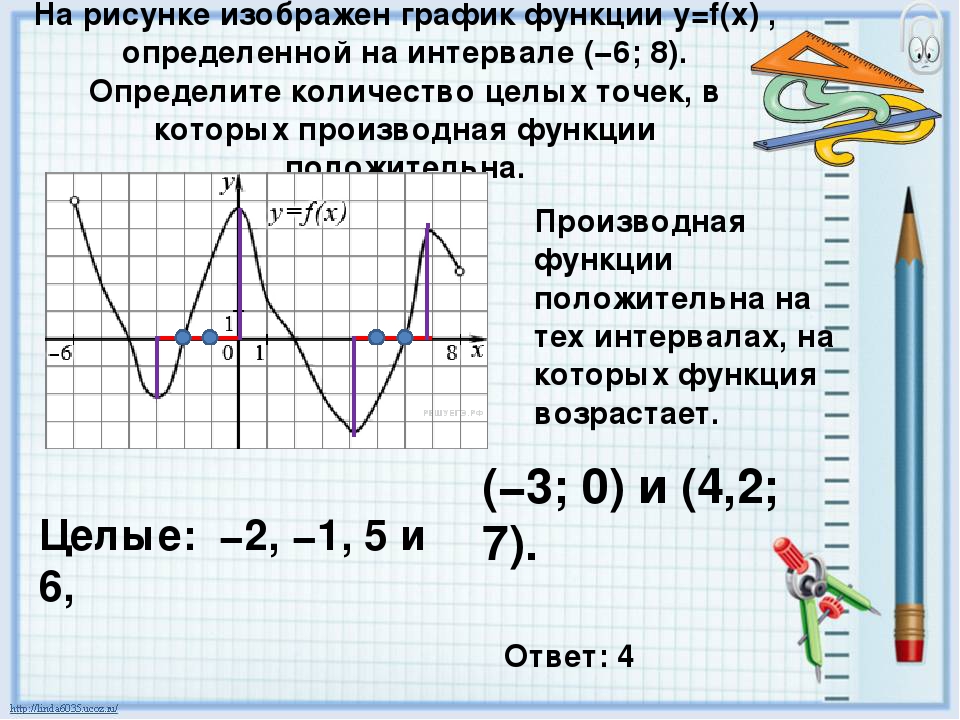 00000
 пересечение по оси x = 9/1 = 9,00000 
 Расчет наклона: 
 Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно -9,000, а для x = 2,000 значение y равно -7,000. Итак, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на -7000 — (-9000) = 2.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
 Наклон = 2.000 / 2.000 = 1.000 
 Геометрическая фигура: прямая линия 
 Наклон = 2.000 / 2.000 = 1.000
 пересечение по оси x = 9/1 = 9,00000
 пересечение по оси y = -9/1 = -9,00000
 Почему узнать об этом 
 Термины и темы 
 Ссылки по теме 
 Родительские функции — Типы, свойства и примеры 
 При работе с функциями и их графиками вы заметите, как графики большинства функций выглядят одинаково и следуют схожим шаблонам.Это потому, что функции, имеющие одинаковую степень, будут следовать аналогичной кривой и использовать одни и те же родительские функции.
   Родительская функция представляет собой простейшую форму семейства функций.  
 Это определение прекрасно описывает родительские функции. Мы используем родительские функции, чтобы направлять нас при построении графиков функций, которые находятся в том же семействе. В этой статье мы:
 Рассмотрим все уникальные родительские функции (возможно, вы уже сталкивались с некоторыми ранее).
 Узнайте, как определить родительскую функцию, которой принадлежит функция.
 Возможность идентифицировать и графически отображать функции с помощью их родительских функций может помочь нам лучше понять функции, так чего же мы ждем?
 Что такое родительская функция? 
 Теперь, когда мы понимаем, насколько важно для нас овладеть различными типами родительских функций, давайте сначала начнем понимать, что такое родительские функции и как их семейства функций зависят от их свойств.
 Определение родительской функции 
 Родительские функции — это простейшая форма  данного семейства функций . Семейство функций — это группа функций, которые имеют одинаковую наивысшую степень  и, следовательно, одинаковую форму для своих графиков .
 На приведенном выше графике показаны четыре графика, которые демонстрируют U-образный график, который мы называем параболой. Поскольку все они имеют одинаковую высшую степень двойки и одинаковую форму, мы можем сгруппировать их в одно семейство функций.Сможете угадать, к какой семье они принадлежат?
 Все эти четыре функции являются квадратичными, и их простейшая форма будет y = x  2 . Следовательно, родительская функция для этого семейства — y = x  2 .
 Поскольку родительские функции являются простейшей формой данной группы функций, они могут сразу дать вам представление о том, как будет выглядеть данная функция из того же семейства.
 Какие бывают типы родительских функций? 
 Пришло время освежить наши знания о функциях, а также узнать о новых функциях.Как мы уже упоминали, знакомство с известными родительскими функциями поможет нам лучше и быстрее понять и построить графики функций.
 Почему бы нам не начать с тех, которые мы, возможно, уже узнали в прошлом?
 Первые четыре родительские функции содержат многочлены с возрастающей степенью. Давайте посмотрим, как ведут себя их графики, и отметим область и диапазон соответствующих родительских функций.
 Функции констант 
 Функции констант — это функции, которые определяются своей соответствующей константой c.Все постоянные функции будут иметь горизонтальную линию в качестве графика и содержать только константу в качестве члена.
 Все постоянные функции будут иметь все действительные числа в качестве домена и y = c в качестве диапазона. У каждого из них также есть точка пересечения по оси y в точке (0, c).
 Движение объекта в состоянии покоя — хороший пример постоянной функции.
 Линейные функции 
 Линейные функции содержат x как член с наивысшей степенью и общую форму y = a + bx.Все линейные функции имеют прямую линию  в виде графика .
 Родительская функция  линейных функций — это y = x, , и она проходит через начало координат. Область и диапазон всех линейных функций: , все действительные числа .
 Эти функции представляют отношения между двумя объектами, которые линейно пропорциональны друг другу.
 Квадратичные функции 
 Квадратичные функции — это функции, у которых  2 является высшей степенью .Все квадратичные функции возвращают параболу  в качестве своего графика . Как обсуждалось в предыдущем разделе, у квадратичных функций  y = x  2  в качестве родительской функции .
 Вершина родительской функции y = x  2  лежит в начале координат. Он также имеет  область всех действительных чисел и диапазон [0, ∞) . Обратите внимание, что эта функция  увеличивается, когда x положительна , и  уменьшается, когда x отрицательна .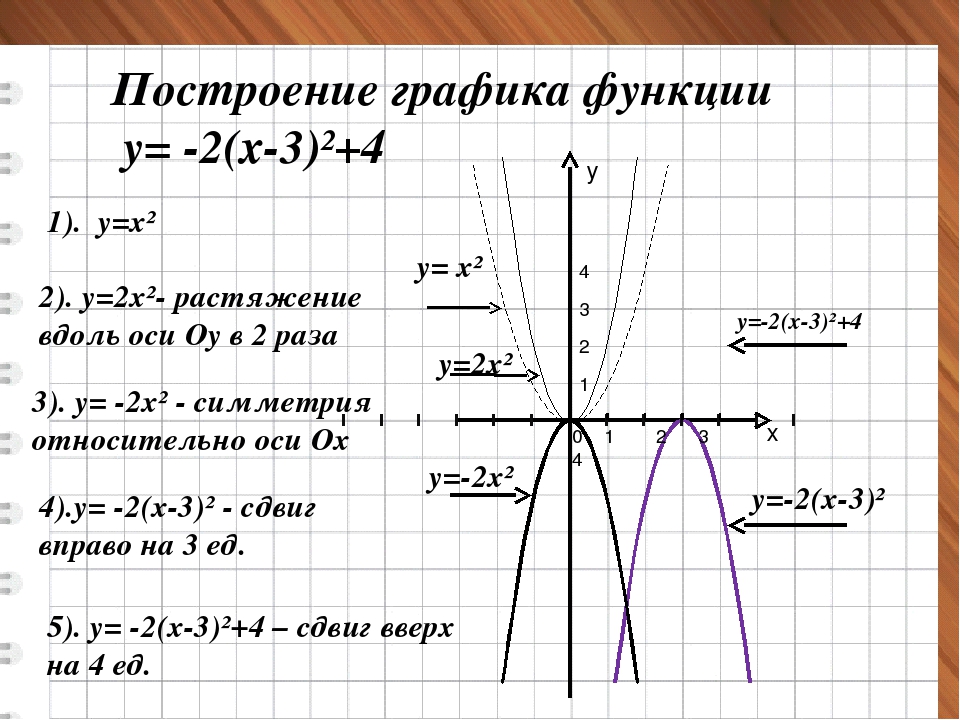
 Хорошим применением квадратичных функций является движение снаряда.Мы можем наблюдать за движением снаряда объекта, построив график квадратичной функции, которая его представляет.
 Кубические функции 
 Давайте перейдем к родительской функции многочленов с  3 наивысшей степенью . Кубические функции имеют общую родительскую функцию  y = x  3  . Эта функция на  увеличивается по всему домену .
 Как и в случае с двумя предыдущими родительскими функциями, график y = x  3  также проходит через начало координат.Его домен  и диапазон равны (-∞, ∞)  или также все действительные числа.
 Функции абсолютного значения 
 Родительская функция функций абсолютного значения —  y = | x | . Как показано на графике родительской функции, функции абсолютного значения должны возвращать  V-образные графики .
 Вершина y = | x | также находится в начале координат.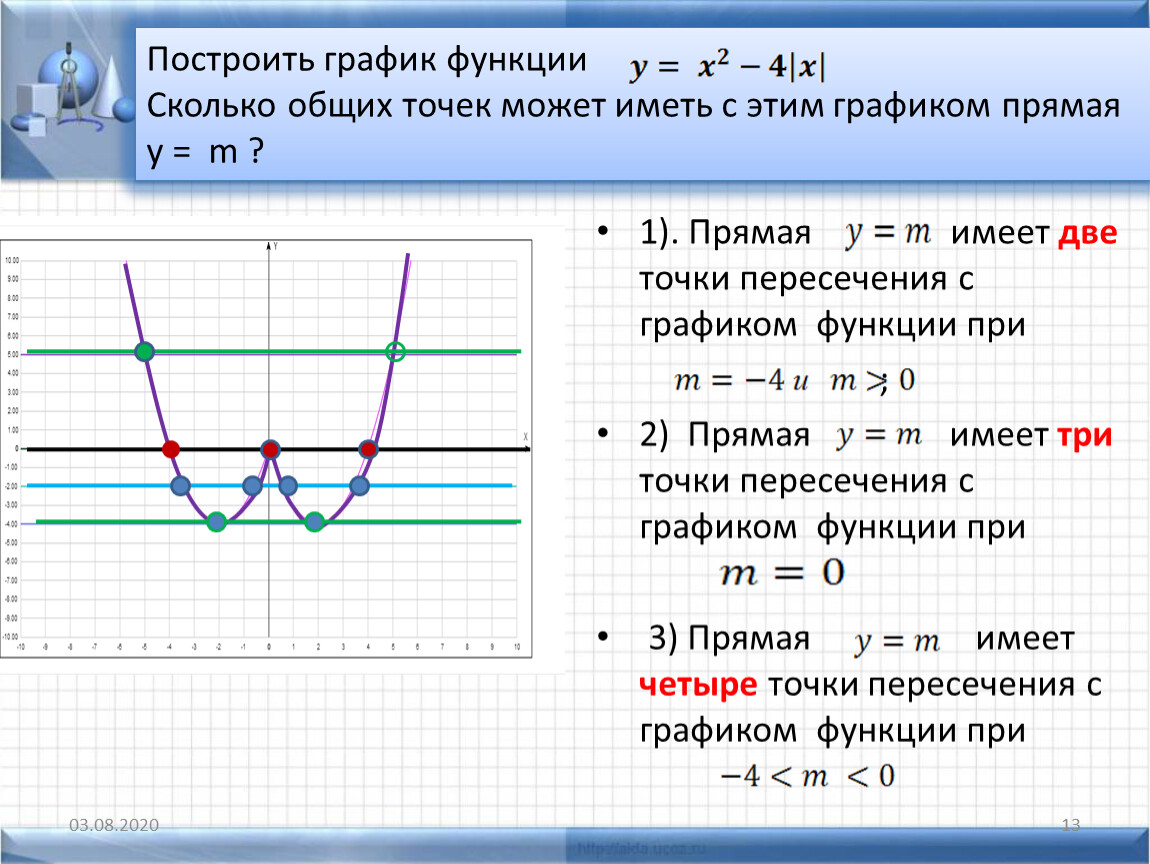 Поскольку он проходит на обоих концах оси x,  y = | x | имеет область в (-∞, ∞). Абсолютные значения никогда не могут быть отрицательными, поэтому родительская функция  имеет диапазон [0, ∞) .
 Мы используем функции абсолютного значения, чтобы подчеркнуть, что значение функции всегда должно быть положительным.
 Радикальные функции 
 Двумя наиболее часто используемыми радикальными функциями являются функции извлечения квадратного корня  и кубического корня .
 Родительская функция функции извлечения квадратного корня —  y = √x . Его график показывает, что его значения x и y никогда не могут быть отрицательными.
 Это означает, что область  и диапазон y = √x равны [0,  ∞ ) . Начальная точка или вершина родительской функции также находится в  в начале координат . Родительская функция y = √x также увеличивается на  во всей области .
 Давайте теперь изучим родительскую функцию функций кубического корня. Подобно функции извлечения квадратного корня, ее родительская функция  выражается как y =   ∛   x .
 На графике показано, что родительская функция имеет домен  и диапазон (-∞, ∞) .Мы также можем видеть, что y = ∛x составляет , увеличиваясь во всей области .
 Экспоненциальные функции 
 Экспоненциальные функции — это функции, в экспоненте которых есть алгебраические выражения. Их родительская функция  может быть выражена как y = b  x  , где b может быть любой ненулевой константой. График родительской функции,  y = e  x ,  показан ниже, и из него мы видим, что  никогда не будет равно 0 .
 И когда x = 0, y проходит через ось y при y = 1.Мы также можем видеть, что родительская функция никогда не находится ниже оси Y, поэтому  ее диапазон составляет (0,  ∞ ).  Его домен , однако,   может быть полностью действительным числом . Мы также можем видеть, что эта функция на  увеличивается во всем домене. 
 Одним из наиболее распространенных приложений экспоненциальных функций является моделирование роста населения и сложных процентов.
 Логарифмические функции 
 Логарифмические функции являются функциями, обратными экспоненциальным функциям. Его родительская функция может быть выражена как y = log  b  x , где b — ненулевая положительная константа. Давайте посмотрим на график, когда  b = 2 .
 Как и экспоненциальная функция, мы можем видеть, что x никогда не может быть меньше или равным нулю для y = log  2  x. Следовательно,  его домен (0, ∞) . Однако его диапазон  содержит все действительные числа . Мы также можем видеть, что эта функция на  увеличивается во всем домене. 
 Мы используем логарифмические функции для моделирования природных явлений, таких как сила землетрясения.Мы также применяем его при вычислении скорости распада периода полураспада в физике и химии.
 Взаимные функции 
 Взаимные функции — это функции, которые содержат числитель констант и знаменатель x. Его родительская функция —  y = 1 / x .
 Как видно из графика, ни x, ни y никогда не могут быть равны нулю. Это означает, что его домен  и диапазон равны (-∞, 0) U (0, ∞) . Мы также можем видеть, что функция на  убывает во всей области .
 На протяжении всего нашего пути с функциями и графиками есть много других родительских функций, но эти восемь родительских функций относятся к , наиболее часто используемым и обсуждаемым функциям .
 Вы даже можете резюмировать то, что вы узнали, создав таблицу, показывающую все свойства родительских функций.
 Как найти родительскую функцию? 
 Что делать, если нам дана функция или ее график, и нам нужно идентифицировать ее родительскую функцию? Мы можем сделать это, запомнив важные свойства каждой функции и определив, какие из родительских графиков, которые мы обсуждали, соответствуют заданному.
 Вот несколько наводящих вопросов, которые могут нам помочь:
 Какая наивысшая степень функции?
 Содержит ли он квадратный корень или кубический корень?
 Функция находится в экспоненте или знаменателе?
 График функции увеличивается или уменьшается?
 Каков домен или диапазон функции?
 Если мы сможем ответить на некоторые из этих вопросов путем проверки, мы сможем вывести наши варианты и в конечном итоге идентифицировать родительскую функцию.
 Давайте попробуем f (x) = 5 (x — 1)  2 . Мы видим, что  наивысшая степень f (x) равна 2 , поэтому мы знаем, что эта функция является квадратичной функцией. Следовательно,  его родительская функция y = x  2  .
 Почему бы нам не построить график f (x) и также не подтвердить наш ответ?
 На графике мы видим, что он образует параболу, подтверждая, что его родительская функция равна y = x  2 .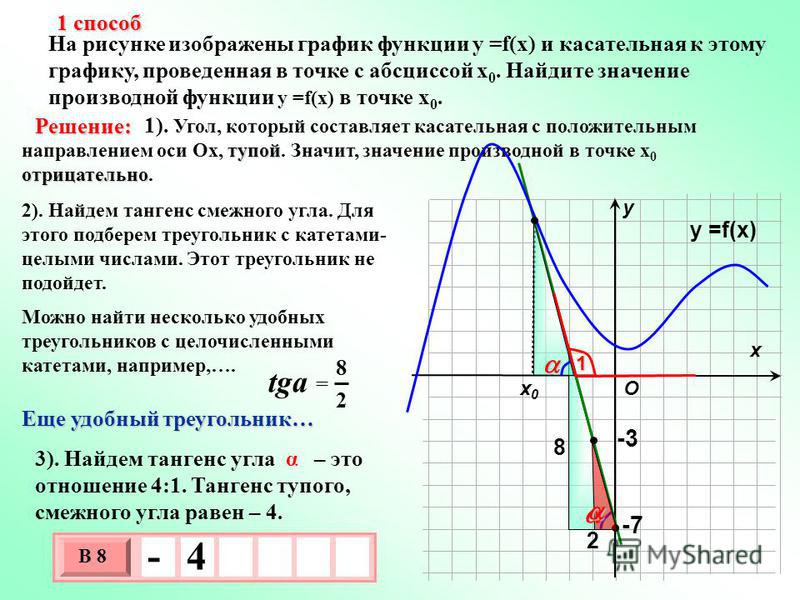
 Просмотрите первые несколько разделов этой статьи и свои собственные заметки, а затем давайте попробуем задать несколько вопросов, чтобы проверить наши знания о родительских функциях.
   Пример 1  
 Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
  Решение 
 Функции, представленные графиками A, B, C и E, имеют аналогичную форму, но смещены вверх или вниз. Фактически, эти функции представляют собой семейство  экспоненциальных функций . Это означает, что все они  имеют общую родительскую функцию: y = b  x .
 С другой стороны, график D представляет логарифмическую функцию, поэтому  D не принадлежит  к группе экспоненциальных функций.
   Пример 2  
 Какие из следующих функций не принадлежат к данному семейству функций?
 y = 5x  2 
 y = -2x  2  + 3x — 1
 y = x (3x  2 )
 y = (x — 1) (x + 1)
  Решение 
 Функция y = 5x  2  имеет наивысшую степень двойки, поэтому она является квадратичной функцией. Это означает, что его родительская функция y = x  2 . То же самое и для y = -2x  2  + 3x — 1. Исходя из этого, мы можем подтвердить, что рассматриваем семейство квадратичных функций.
 Применяя разность полных квадратов к четвертому варианту, получаем y = x  2  — 1. Это также квадратичная функция. Остается третий вариант.
 В развернутом виде y = x (3x  2 ) становится y = 3x  3, , и это показывает, что наивысшая степень равна 3.Следовательно, он не может быть частью данного семейства функций.
   Пример 3  
     Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
  Решение 
 Начнем с f (x). Мы можем видеть, что у него есть парабола для своего графика, поэтому мы можем сказать, что  f (x) является квадратичной функцией .
 Это означает, что f (x) имеет родительскую функцию  y = x  2  .
 График простирается по обе стороны от x, поэтому он имеет область    (-∞, ∞) .
 Парабола никогда не опускается ниже оси x, поэтому ее диапазон  составляет [0, ∞) .
 Основываясь на графике, мы видим, что значения x и y функции g (x) никогда не будут отрицательными. Они также показывают возрастающую кривую, которая напоминает график  функции квадратного корня .
 Следовательно, родительская функция  для g (x) равна   y = √x .
 График простирается до правой части x и никогда не может быть меньше 2, поэтому он имеет область    [2, ∞) .
 Парабола никогда не опускается ниже оси x, поэтому ее диапазон  составляет [0, ∞) .
 График h (x) показывает, что их значения x и y никогда не будут равны 0. Симметричные кривые также похожи на график обратных функций.
 Это означает, что  h (x) имеет родительскую функцию y = 1 / x. 
 Пока x и y никогда не равны нулю, h (x) по-прежнему действителен, поэтому он имеет как домен , так и диапазон   (-∞, ∞) .
 Прямые линии, представляющие i (x), говорят о том, что это линейная функция.
 Он имеет родительскую функцию  y = x. 
 График простирается по обе стороны от x и y, поэтому он имеет область  и диапазон   (-∞, ∞) .
   Пример 4  
 Определите родительскую функцию для следующих функций.
 f (x) = x  3  — 2x + 1
 g (x) = 3√x + 1
 h (x) = 4 / x
 i (x) = e  x + 1 
  Решение 
 Наивысшая степень f (x) равна 3, поэтому это кубическая функция.Это означает, что у него есть родительская функция  y = x  3  .
 Функция g (x) имеет радикальное выражение 3√x. Поскольку у нее есть член с квадратным корнем, функция является функцией с квадратным корнем и имеет родительскую функцию  y = √x. 
 Мы видим, что x находится в знаменателе h (x), поэтому он обратный. Следовательно, его родительская функция —  y = 1 / x .
 Показатели степени содержат x, поэтому одно это говорит нам о том, что i (x) — экспоненциальная функция.Следовательно, его родительская функция может быть выражена как y = b  x , где b — константа. Для случая i (x) у нас есть  y = e  x   в качестве его родительской функции.
 Практические вопросы 
 1. Графики пяти функций показаны ниже. Какие из следующих функций не относятся к данному семейству функций?
 2. Какие из следующих функций не относятся к данному семейству функций?
 y = 4x  3 
 y = -3x  3  + 4x  2  + 5x — 1
 y = x (5x  2 )
 y = (x — 1) (x + 1) (х + 2)
 3. Определите родительскую функцию следующих функций.
 f (x) = x  3  — 2x + 1
 g (x) = 3√x + 1
 h (x) = 1 / (x + 1)
 i (x) = e  x + 1 
 4. Определите родительскую функцию следующих функций на основе их графиков. Также определите область и диапазон каждой функции.
 5. Опишите разницу между f (x) = -5 (x — 1)  2  и его родительской функцией. Каков домен и диапазон f (x)?
 6.Пусть a и b — две ненулевые константы. Опишите разницу между g (x) = ax + b и его родительской функцией. Каков домен и диапазон f (x)?
 
  Изображения / математические рисунки создаются с помощью GeoGebra. 
 Предыдущий урок | Главная страница | Следующий урок 
 Когда именно XY не равно YX? 
 Мой ответ на вопрос на Quora:  Когда именно xy не равно yx? 
 Выражение \ (xy \) может использоваться в различных ситуациях для различных видов математических объектов (не только для чисел!) И операций над ними, и во многих (если не в большинстве) ситуаций \ (xy \) является не равно \ (yx \).
 Пусть \ (x \) и \ (y \) — два процесса или операции, а \ (xy \) — результат их последовательного применения: сначала \ (x \), затем \ (y \). Пример «реальной жизни» уровня детского сада:
 \ (x \) надевает носок на левую ногу, а \ (y \) надевает носок на правую ногу; Совершенно очевидно, что порядок работы не имеет значения, \ (xy = yx \).
 \ (x \) надевает носок на левую ногу, а \ (y \) надевает ботинок на ту же ногу. Вы, наверное, согласитесь, что \ (xy \ ne yx \).
 В геометрии результат композиции (то есть последовательного применения) вращений и других геометрических преобразований в пространстве почти всегда зависит от порядка, в котором они выполняются. Эти вращения и их последовательное выполнение описываются как матрицы (определенные таблицы чисел) и их умножение (определенное некоторыми конкретными правилами) — и, как следствие, для умножения матриц в большинстве случаев результат зависит от порядка умножаемых. , \ (ху \ не ух \).