Построение точек в пространстве по координатам онлайн: 3D Calculator — GeoGebra

Онлайн калькулятор: Системы координат в пространстве

Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах:

• Прямоугольной (декартовой)
• Цилиндрической
• Сферической
  Прямоугольная, цилиндрическая и сферическая системы координат

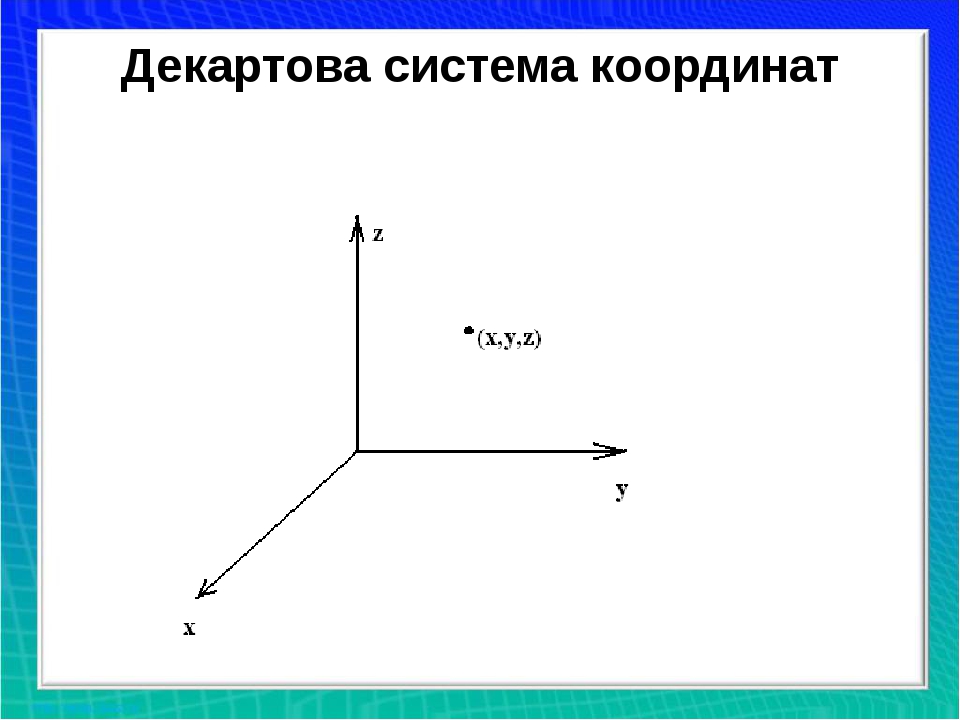
Прямоугольная система координат

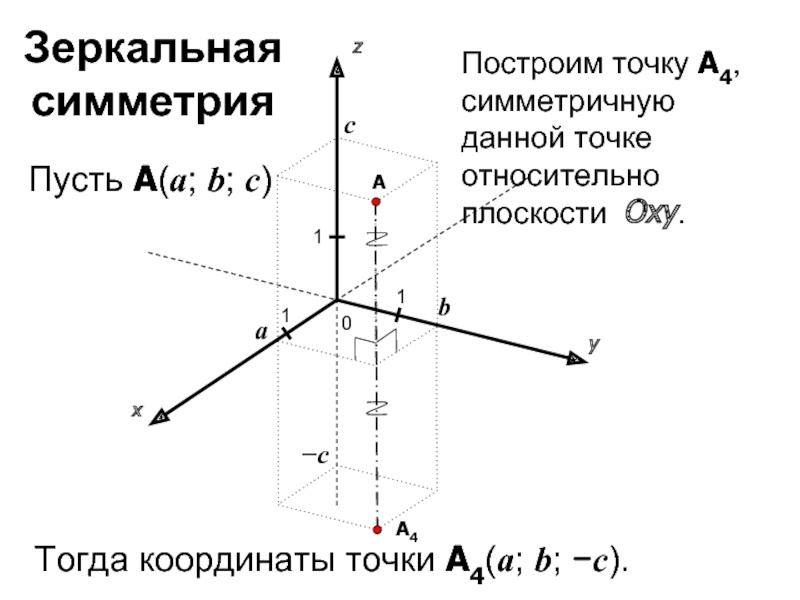
Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат.

Цилндрическая система координат

Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r — всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z. Азимутальный угол φ — значение в диапазоне 0 ..360 градусов — определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.

Сферическая система координат

Определяет точку в пространстве при помощи радиуса ρ, азимута φ, и полярного угла θ. Азимут φ совпадает со значением азимута в цилиндрических координатах. Радиус ρ — расстояние от центра координат, до точки. Полярный угол образован положительной полуосью z и радиусом из центра координат до точки в пространстве.

Прямоугольные координаты в пространстве

Точность вычисления

Знаков после запятой: 2

Цилиндрические координаты

Азимут (φ), градусы

 

Сферические координаты

Азимут (φ), градусы

 

Полярный угол (θ), градусы

 

content_copy Ссылка save Сохранить extension Виджет

Формулы преобразования декартовых координат

Радиус в цилиндрической системе:

Радиус в сферической системе:

Азимут:
, см Арктангенс с двумя аргументами

Полярный угол:

Цилиндрические координаты

Точность вычисления

Знаков после запятой: 2

Прямоугольные координаты

Сферические координаты

Азимут (φ), градусы

 

Полярный угол (θ), градусы

 

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:

Записать канонические уравнения прямой, заданной уравнениями двух плоскостей

.

Вы задаете коэффициенты уравнений плоскостей, калькулятор выдает уравнения прямой в канонической форме. Немного теории, как обычно, можно почерпнуть под калькулятором

Нахождение уравнений прямой, заданной пересечением двух плоскостей

Канонические уравнения прямой

 

Точность вычисления

Знаков после запятой: 2

content_copy Ссылка save Сохранить extension Виджет

Канонические уравнения прямой, заданной пересечением двух плоскостей

Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.

Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль.

Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.

Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .

Точка и вектор дают нам канонические уравнения прямой:

Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.

В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:

В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:

Эти случаи также учитываются калькулятором.

Построение геометрических фигур по точкам на координатной плоскости

Данная программа позволит Вам построить практически любой многоугольник. Все что Вам надо сделать, это ввести количество точек, которые Вы хотите соединить, затем ввести их координаты и программа построит Вашу геометрическую фигуру на координатной плоскости.

Сейчас Вам нужно выбрать количество точек, которое Вы хотите соединить. Помните, что фигура должна быть замкнута, тоесть ломаная должна начинаться и заканчиваться одной и той же точкой. Суммарное количество точек будет на 1 больше количества вершин многоугольника.

Также, при помощи нашей программы, можно просто строить фигуры, делать чертежи к задачам. Для этого надо указать, что Вы хотите убрать координатные оси и не хотите около каждой точки писать ее координаты. Для таких рисунков Вам понадобится размеченая плоскость, для узнавания точек, которые вы хотите соединить.

Ниже Вы можете посмотреть примеры использования программы!

Сколько точек Вы хотите соединить?

Примеры использования программы

1) Изображение схемотичного рисунка к задаче. Подобный рисунок был нужен, когда на нашем форуме просили решить задачу — тема на форуме.

Рисунок к данной задаче.

Для того, чтобы наисовать такую схему нужно отменить координатные оси и отменить писание координат точек.

2) Рисунок к задаче, построение фигуры по точкам. Наример построение высоты в треугольнике.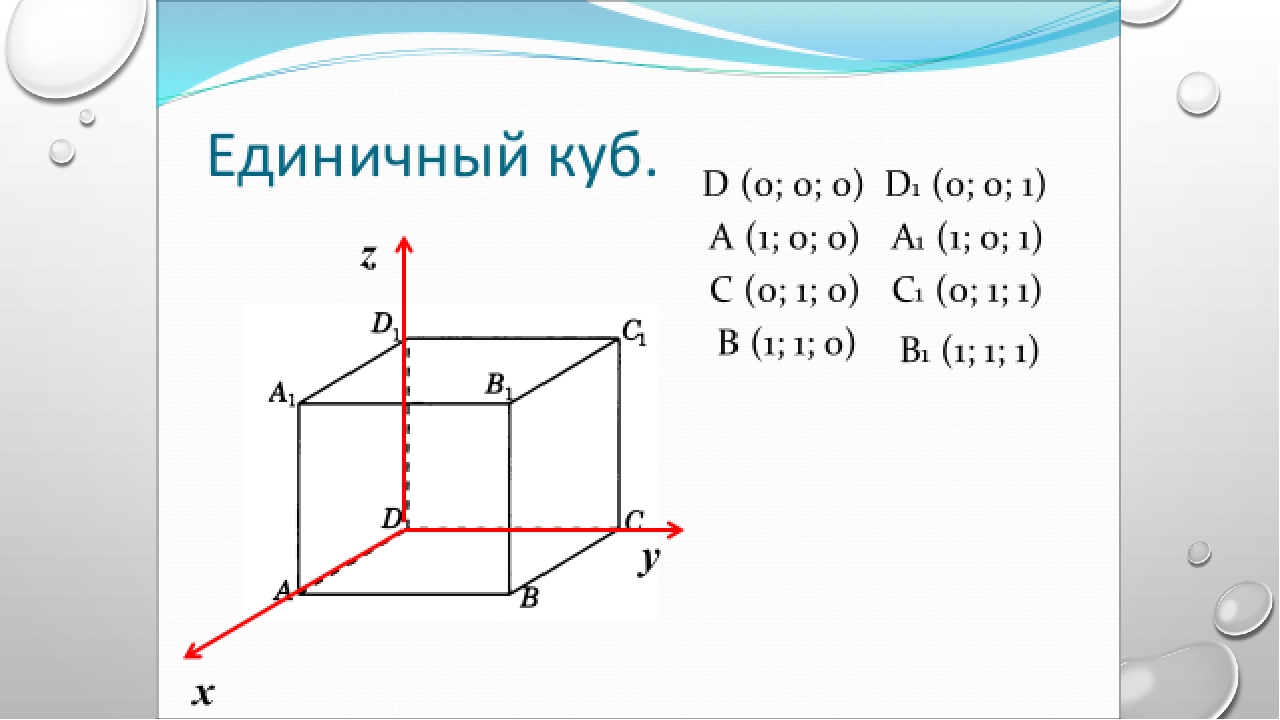

Рисунок к данной задаче.

Программа имеет много применений, только надо включить фантазию!

Если после использования данного онлайн калькулятора (Построение геометрических фигур по точкам) у Вас возникли какие-то вопросы по работе сервиса или вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.

Вы поняли, как решать? Нет?

Помощь с решением

Отображение координат на декартовой плоскости

Запутались при нанесении координат на декартовой плоскости?

Нанесение координат на сетку или декартовую плоскость может сбивать с толку учащихся и вызывать у них стресс, но это не обязательно! Этот сайт поможет вам сделать УДОВОЛЬСТВИЕ!

Перед тем, как начать увлекательную практику построения графика, важно понять числовые линии, составляющие оси x и y .Каждая точка в координатной сетке имеет уникальный набор из 2 координат, позволяющих определить ее местоположение. Этот уникальный набор координат состоит из координаты x , которая определяет положение точки по горизонтали, и координаты y , которая определяет ее положение по вертикали на сетке. Это способ математического отображения позиций на 2-мерной плоскости. Дополнительные сведения см. На странице «Основы построения графиков»

.

ДЕМО

Этот сайт предназначен для учащихся средних и средних школ, родителей и учителей —

• для понимания декартовой плоскости или координатной сетки
• для последовательного построения x / y координат точно
• , чтобы предоставить учителям стратегии, способствующие успешному развитию
  нанесение координат в всех четырех квадрантах для всех учеников
• и обеспечить веселых межучебных мероприятий , которые обеспечивают
  необходимо практиковать это умение в течение года.

ПРИМЕЧАНИЕ:

Этот сайт начинался как ресурс для построения упорядоченных пар во всех четырех квадрантах, но я рад сообщить, что в настоящее время он расширяется за счет практики построения графиков CoordinArt, которая ограничена Quadrant I !

Поскольку мои проекты настолько подробны, что они требуют времени для завершения,

ПОЖАЛУЙСТА, запланируйте минимум 2 дня для большей части. Обычно я провожу один день в классе, а затем через несколько дней сдаю готовый дизайн!

CoordinArt News

Новости CoordinArt предоставляют последние доступные дизайны CoordinArt.CoordinArt создает уникальные изображения, вычерчивая наборы упорядоченных пар и нанося их на координатную сетку! Веселое обучение происходит

Полный список CoordinArt

Полный список доступных CoordinArt (изображения, сделанные из упорядоченных пар в координатной сетке). Соединения точки с точкой создают потрясающие изображения.

CoordiinArt Intro

CoordinArt Intro знакомит вас с создателем CoordinArt Нэнси Коу. Узнайте, как она начала создавать проекты CoordinArt.

Основы построения графиков

Изучите основы построения графиков для точного нанесения любой упорядоченной пары координат x и y на координатную сетку. Включает все четыре квадранта

Coordinart-Fun Plotting Practice

Студентам необходимо попрактиковаться в построении координат во всех четырех квадрантах. Выбирайте из множества заданий, которые создают картину, относящуюся к различным межучебным темам.

CoordinArt-Monthly

CoordinArt-Monthly упорядочивает CoordinArt по календарным месяцам, чтобы быстро найти способ построения графиков на основе праздников каждого месяца..

CoordinArt — Патриотические темы

CoordinArt — Patriotic предлагает разнообразные практики рисования x / y на патриотическую тематику во всех четырех квадрантах декартовой плоскости.

координатыХудожественные достопримечательности

Создание координатной сетки Эйфелевой башни и ориентиров в CoordinArt. Веселая практика построения графиков, которую можно использовать в течение всего года. Составляет отличные альтернативные планы уроков!

Координатор Арт-животные

Выберите CoordinArt-animals для практики рисования координат, которая также позволяет легко дифференцированно обучать в вашем классе.Простые, но реалистичные животные в одно- или четырехквадрантном формате.

Координатор Art-Misc

Темы CoordinArt-Misc, в том числе Эдвард из серии «Сумерки». Уникальная практика построения графиков, позволяющая создавать реалистичные изображения на координатной сетке. Отличный план урока оставить на саб.

Первый квадрант участок

Дизайн рисунков координатной сетки для построения первого квадранта. Используются только положительные координаты x / y. Они подходят для начального среднего уровня и представляют собой планы уроков на короткие сроки.

Easy Quadrant-I

Easy Quadrant-I CoordinArt обеспечивает практику построения графиков, в которой используются ТОЛЬКО положительные целые числа для координат x и y . Создаются новые дизайны, так что заходите почаще.

Дифференцированная инструкция

Наборы дифференцированных инструкций CoordinArt позволяют легко дифференцировать обучение в вашем классе. Каждый дизайн предоставляется ТОЛЬКО для квадранта I и для всех ЧЕТЫРЕХ квадрантов.

свяжитесь со мной

Свяжитесь со мной, чтобы сообщить о теме CoordinArt, которая вам нужна. Я был бы счастлив сделать его своим следующим проектом!

Отзывы

Отзывы пользователей дизайнов CoordinArt. Пользователи делятся опытом своих учеников по созданию изображений координатной сетки.

Студенты говорят

Студенты высказываются, когда им предоставляется возможность похвастаться завершенным CoordinArt (изображения в координатной сетке).

Студенческая галерея

Студенческая галерея — это коллекция законченных CoordinArt, выполненных студентами.Креативность широко открыта с множеством дизайнов, чтобы каждый ученик мог сделать каждый дизайн CoordinArt своим!

Поиск широты и долготы на карте Получение координат

Что такое широта и долгота?

Точно так же, как каждый реальный дом имеет свой адрес (который включает номер, название улицы, города и т. Д.), Каждая точка на поверхности земли может быть указана с координатами широты и долготы.Следовательно, используя широту и долготу, мы можем указать практически любую точку на Земле.

Широта имеет обозначение phi и показывает угол между прямой линией в определенной точке и экваториальной плоскостью. Широта указывается в градусах, начиная с 0 ° и заканчивая 90 ° по обе стороны от экватора, что делает широту северной и южной. Экватор — это линия с широтой 0 °. Долгота имеет символ лямбды и является другой угловой координатой, определяющей положение точки на поверхности земли.Долгота определяется как угол, указывающий на запад или восток от Гринвичского меридиана, который принимается за нулевой меридиан. Долгота может быть определена как максимум 180 ° к востоку от нулевого меридиана и 180 ° к западу от нулевого меридиана.

Широта и долгота измеряются в градусе , которые, в свою очередь, делятся на минуты и секунды.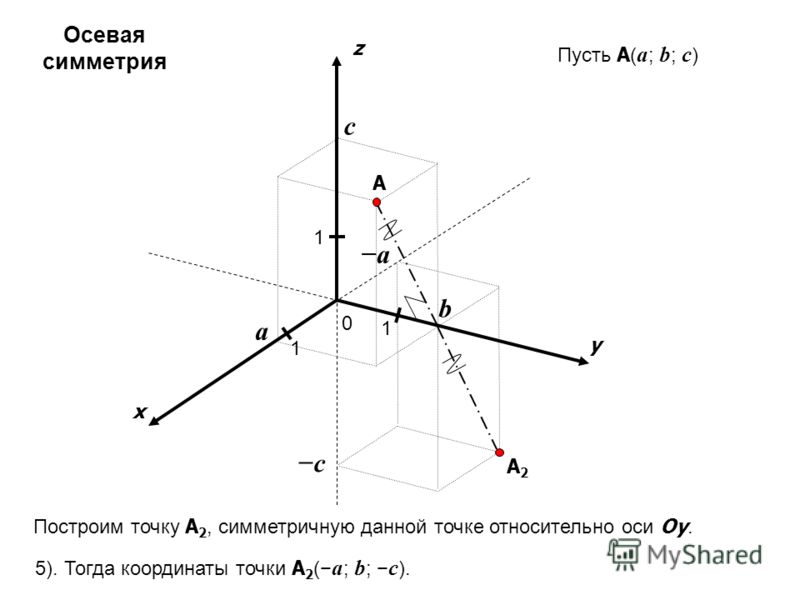 Например, тропическая зона, расположенная к югу и к северу от экватора, определяется пределами 23 ° 26’13.7 » южной широты и 23 ° 26’13.7 » северной широты. Например, географические координаты горы Нгаурухо в Новой Зеландии, известной тем, что здесь снимали фильм «Властелин колец», имеют географические координаты 39 ° 09’24,6»S 175 ° 37’55,8»E. .

О широте и долготе

Latlong.net — это географический онлайн-инструмент , который можно использовать для поиска широты и долготы места и получения его координат на карте. Вы можете искать место по названию города или населенного пункта, а также по названию особых мест, и правильные координаты широты и долготы будут отображаться в нижней части формы поиска широты и долготы.При этом найденное вами место будет отображаться с маркером точки в центре карты. Также под картой будут отображаться координаты gps .

точек построения на координатной плоскости

Точки, которые следует помнить при нанесении данных точек на координатную плоскость:

• Если заданная точка имеет форму (+, +), то она будет расположена в 1-м квадранте

• Если данная точка в виде (-, +), то она будет расположена во 2-м квадранте

• Если данная точка имеет вид (-, -), то она будет расположена в 3-м квадранте

• Если заданная точка имеет вид (+, -), тогда она будет расположена в 4-м квадранте

• Если данная точка имеет значение 0 в координате x, то она будет расположена на оси y.

• Если данная точка имеет значение 0 в координате y, то она будет расположена на оси x.

Давайте посмотрим на несколько примеров, основанных на вышеупомянутой концепции.

Пример 1:

Постройте точку (-2, 2) на координатной плоскости.

Решение:

Данная точка имеет форму (-, +), поэтому она будет расположена во 2-м квадранте.

Пример 2:

Постройте точку (4, -2) на координатной плоскости.

Решение:

Данная точка имеет форму (+, -), поэтому она будет расположена в 4-м квадранте.

Пример 3:

Постройте точку (-3, -4) на координатной плоскости.

Решение:

Данная точка имеет форму (-, -), поэтому она будет расположена в 3-м квадранте.

Пример 4:

Запишите упорядоченную пару, которая описывает точку на 12 единиц ниже и на 7 единиц вправо от исходной точки.

Решение:

Для написания необходимой заказанной пары прочтем вопрос еще раз.

12 единиц вниз ==> -12

7 единиц вправо ==> + 7

Следовательно, требуемая точка (-12, 7)

Пример 5:

Запишите упорядоченную пару для точки то есть на 9 единиц слева от начала координат и лежит на оси x.

Решение:

Чтобы записать нужную заказанную пару, прочтем вопрос еще раз.

9 единиц слева от начала координат ==> -9

Он лежит на оси абсцисс. Таким образом, значение координаты y будет 0.

Следовательно, требуемая точка будет (-9, 0)

Пример 6:

На диаграмме справа показано положение артефактов, обнаруженных на дне океана. Напишите координаты места для каждого объекта: монеты, тарелки, кубка и вазы.

Решение:

Пример 7:

Постройте точку (0, -1) на координатной плоскости.

Решение:

В данной точке значение координаты x равно 0. Таким образом, требуемая точка должна располагаться на оси y.

Пример 8:

Постройте точку (5, 0) на координатной плоскости.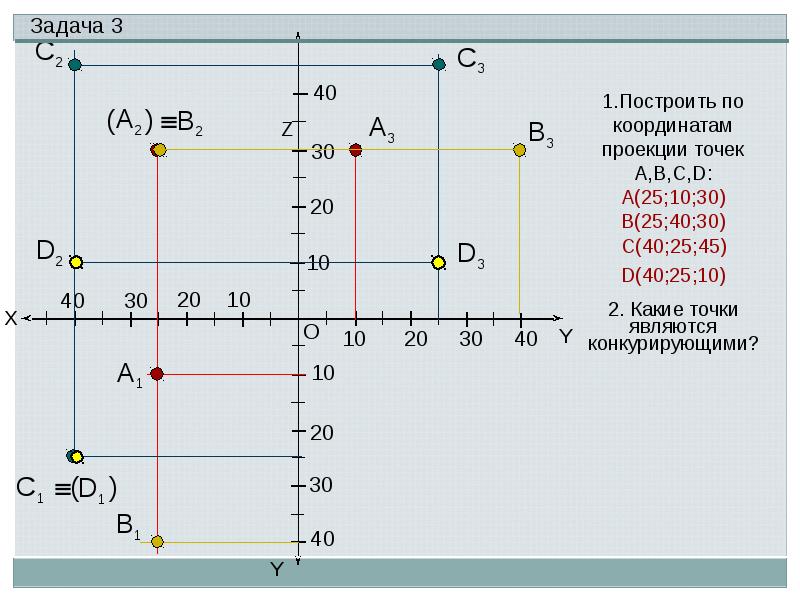

Решение:

В данной точке значение координаты x равно 0. Таким образом, требуемая точка должна располагаться на оси y.

Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.

Если у вас есть отзывы о наших математических материалах, напишите нам:

[email protected]

Мы всегда ценим ваши отзывы.

Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.

ЗАДАЧИ СО СЛОВАМИ

Задачи со словами HCF и LCM

Задачи со словами на простых уравнениях

Задачи со словами на линейных уравнениях

Задачи со словами на квадратных уравнениях

Задачи со словами

Проблемы со словами в поездах

Проблемы со словами по площади и периметру

Проблемы со словами по прямому и обратному изменению

Проблемы со словами по цене за единицу

Проблемы со словами по скорости за единицу

задачи по сравнению ставок

Преобразование обычных единиц Word задачи

Преобразование метрических единиц Word задачи

Word задачи по простому проценту

Word задачи по сложным процентам

Word задачи по типам ngles

Проблемы с дополнительными и дополнительными углами

Проблемы со словами с двойными фактами

Проблемы со словами тригонометрии

Проблемы со словами в процентах

Проблемы со словами

и Задачи

Задачи с десятичными словами

Задачи со словами о дробях

Задачи со словами о смешанных фракциях

Одношаговые задачи с уравнениями со словами

Проблемы со словами с линейным неравенством

Задачи

Проблемы со временем и рабочими словами

Задачи со словами на множествах и диаграммах Венна

Задачи со словами на возрастах

Теорема Пифагора Задачи со словами

Процент числового слова проблемы

Проблемы со словами при постоянной скорости

Проблемы со словами при средней скорости

Проблемы со словами при сумме углов треугольника 180 градусов

ДРУГИЕ ТЕМЫ

Сокращения прибыли и убытков

Сокращения в процентах

Сокращения в таблице времен

Сокращения времени, скорости и расстояния

Сокращения соотношения и пропорции

Область и диапазон рациональных функций

Область и диапазон рациональных функций функции с отверстиями

График рациональных функций

График рациональных функций с отверстиями

Преобразование повторяющихся десятичных знаков в дроби

Десятичное представление рациональных чисел

Поиск корня из длинного квадрата видение

L. Метод CM для решения задач времени и работы

Преобразование задач со словами в алгебраические выражения

Остаток при делении 2 в степени 256 на 17

Остаток при делении в степени 17 на 16

Сумма всех трехзначных чисел, делимых на 6

Сумма всех трехзначных чисел, делимых на 7

Сумма всех трехзначных чисел, делимых на 8

Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4

Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами

Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3

Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6

GPS-визуализатор

GPS Visualizer — это онлайн-утилита, которая создает карты и профили на основе географических данных. Это бесплатно и проста в использовании, но мощная и чрезвычайно настраиваемая. Ввод может быть в виде данных GPS (треки и путевые точки), маршрутов движения, уличных адресов или простых координат. Используйте его, чтобы увидеть, где вы были, спланировать, куда вы собираетесь, или быстро визуализировать географические данные (научные наблюдения, события, местоположения предприятий, клиентов, недвижимость, фотографии с геотегами и т. Д.). Для настройки дополнительных параметров используйте страницы подробного ввода: Помогите сохранить бесплатный GPS-визуализатор GPS Visualizer — бесплатная услуга, и мы надеемся, что так будет всегда; однако, если вы находите это интересным, экономящим время или просто забавным, вы можете сказать «спасибо» и поощрить дальнейшее развитие, нажав кнопку выше и сделав взнос с помощью кредитной карты или PayPal.Или вы можете отправить элемент списка желаний Amazon. GPS Visualizer может считывать файлы данных из многих различных источников, включая, помимо прочего: GPX (стандартный формат, используемый многими устройствами и программами, включая Garmin eTrex, GPSMAP, Oregon, Dakota, Colorado и серии Nüvi), Google Планета Земля (. kml / .kmz), Маршруты карт Google (URL-адреса), Журналы планеров FAI / IGC , Fugawi (.trk / .wpt), Фуруно , Garmin Fitness (.fit), Garmin Forerunner (.xml / .hst / .tcx), Garmin MapSource / BaseCamp / HomePort (.gdb), Geocaching.com (.loc), Google Таблицы , iGO (.trk), Lowrance (.usr), Таблицы Microsoft Excel (.xls / .xlsx), Данные NMEA 0183 , OziExplorer (.plt / .wpt), Suunto X9 / X9i (.sdf), Timex трейнер , TomTom (.pgl), U-blox (.ubx), XML-каналы , и, конечно же, , разделенный табуляцией или запятыми текст . GPS Visualizer базируется в Портленде, штат Орегон, и доступен в Интернете с октября 2002 года. OpenSnowMap [29.11.20] Листовки и карты Google, созданные с помощью GPS Visualizer, теперь могут отображать лыжные трассы из OpenSnowMap в качестве опции фоновой карты. Улучшения профиля [05/11/20] Теперь вы можете нарисовать профиль высот на карте отдельного трека, используя значок в информационном окне трека. Automatic.com .csv файлы [24.02.20] Файлы экспорта CSV с устройства Connected Car Assistant и приложения для смартфонов Automatic.com теперь можно преобразовать или сопоставить с помощью GPS Visualizer. История местоположений Google [18.02.20] Файлы JSON истории местоположений и семантической истории местоположений из Google Takeout теперь поддерживаются визуализатором GPS. Словацкие, чешские и венгерские карты [01.01.20] Freemap.sk (стилизованные данные OpenStreetMap с затенением и контурными линиями) теперь доступен в качестве фонового параметра в картах Google и Leaflet Maps визуализатора GPS. Данные ASTER v3 [22.12.19] Файлы ASTER DEM на сервере GPS Visualizer были обновлены до версии 3 ASTER, выпущенной в 2019 году. Профили с заполнением [11.11.19] Утилита профиля теперь может рисовать заполненные профили «горных хребтов» в дополнение к линиям; Кроме того, в цветных профилях SVG можно использовать градиенты для получения более плавных и точных цветов.

PPT — 13-5 координат в космосе Презентация PowerPoint, скачать бесплатно

Дэнни Нгуен и Джимми Нгуен 13-5 Координаты в космосе

Объективы пространство. • Используйте формулы расстояния и средней точки для точек в пространстве.

Упорядоченные тройки • В координатной плоскости мы использовали упорядоченную пару с двумя действительными числами для определения точки (x, y) • В пространстве нам нужны 3 действительных числа для построения точки.Это потому, что пространство имеет 3 измерения. Эти числа составляют упорядоченную тройку (x, y, z).

Пространство + • В пространстве оси x, y и z перпендикулярны друг другу. • X представляет глубину • Y представляет ширину • Z представляет высоту • Обратите внимание на график P (2,3,6). _ _ + + _

Пример 1. Построение графика формы в пространстве • Постройте прямоугольное твердое тело, которое содержит точку A (-4,2,4) и начало координат в качестве вершин.

Пример 1: Как построить график формы в пространстве • Сначала постройте координату x.Пройдите 4 единицы в отрицательном направлении. • Затем постройте координату y. Пройдите 2 единицы в положительном направлении. • Наконец, постройте координату z. 4 единицы в положительном направлении • Мы нанесли координату A. • Нарисуйте остальную часть прямоугольной призмы.

Формула расстояния в пространстве • Помните формулу расстояния от координатной плоскости? У нас также есть формула расстояния в космосе.

Доказательство формулы расстояния в пространстве

Пример 2: Формула расстояния • Найдите расстояние между T (6, 0, 0) и Q (-2, 4, 2).

Ваша очередь: (Формула расстояния) • Найдите расстояние между A (3, 1, 4) и B (8, 2, 5) AB AB () + () + () () + () + () Ответ: √27 3 3 OR

Формула средней точки в космосе • У нас также есть формула для средних точек в космосе.

Объяснение формулы средней точки • Среднее значение определяется как средний показатель набора данных.• Когда мы используем формулу средней точки, мы в основном находим среднее значение между координатами x, y и z. • Объединение средних значений в упорядоченную тройку позволяет нам определить, где находится середина сегмента в пространстве.

Пример 3: Формула средней точки • Определите координаты средней точки M отрезка. T (6, 0, 0) и Q (-2, 4, 2)

Ваша очередь: (Формула средней точки) • Найдите координаты средней точки M отрезка AB. A (3, 1, 4) и B (8, 2, 5) = (,,) Ответ: (Секант), шутка: P это (11/2, 3/2, 9/2) или (5 .5, 1.5, 4.5)

Перевод твердого тела • Помните переводы? Вы также можете выполнять переводы в космосе с помощью твердых тел. • Это в основном тот же принцип, который мы видели в гл. 9, за исключением того, что у нас есть другая координата для перевода.

Пример 4: перенос твердого тела • Найдите координаты вершин твердого тела после следующего перемещения. (x, y, z + 20)

Пример 4: Трансляция твердого тела

Расширение с помощью матриц • Мы также должны помнить, что такое дилатация из гл.9. Мы использовали матрицу, чтобы найти координаты изображения после растяжения.