Как построить график функции по уравнению: Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Практика

Содержание

Построение графиков функций

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей,

«Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

при

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

$y=\frac{1}{x}.$

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

$\frac{ \pi }{6}$

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Нули функции: и

Промежутки знакопостоянства функции определим с помощью метода интервалов.

x = 3.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

y = x-4

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты:

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Вот эскиз графика:

y = 1

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При , значение {cos x} равно единице. Значение функции в этих точках будет равно

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при

Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

если или

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

$y\left(2\right)=1, y\left(-2\right)=-y\left(2\right)=-{\rm 1.}$

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции:

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Графиком функции y = a x 2 + b x + c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :

Коэффициент a указывает на то, куда направлены ветки параболы.

Если a > 0 , ветки параболы направлены вверх.
Если a < 0 , ветки параболы направлены вниз.

Коэффициент c указывает, в какой точке парабола пересекает ось y.
Коэффициент b помогает найти x в – координату вершины параболы.

x в = − b 2 a

Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

Если D > 0 – две точки пересечения.
Если D = 0 – одна точка пересечения.
Если D < 0 – нет точек пересечения.

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Функция y = x имеет следующий график:

Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Скачать домашнее задание к уроку 5.

Использование графиков функций при решении уравнений, неравенств, систем.

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Многие задания, которые мы привыкли вычислять чисто алгебраически, можно намного легче и быстрее решить, в этом нам поможет использование графиков функций. Ты скажешь «как так?» чертить что-то, да и что чертить? Поверь мне, иногда это удобнее и проще. Приступим? Начнем с уравнений!

Графическое решение уравнений

Графическое решение линейных уравнений

Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида. Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень. Сейчас же я покажу тебе, как это сделать графическим способом.

Итак, у тебя есть уравнение:

Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:

Обычно, дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат. Иными словами, у нас будет:

А теперь строим. Что у тебя получилось?

Как ты думаешь, что является корнем нашего уравнения? Правильно, координата точки пересечения графиков:

Наш ответ —

Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число !

Как я говорила выше, это самый распространенный вариант, приближенный к алгебраическому решению, но можно решать и по-другому. Для рассмотрения альтернативного решения вернемся к нашему уравнению:

В этот раз не будем ничего переносить из стороны в сторону, а построим графики напрямую, так как они сейчас есть:

Построил? Смотрим!

Что является решением на этот раз? Все верно. Тоже самое — координата точки пересечения графиков:

И, снова наш ответ — .

Как ты видишь, с линейными уравнениями все предельно просто. Настало время рассмотреть что-нибудь посложнее… Например, графическое решение квадратных уравнений.

Графическое решение квадратных уравнений

Итак, теперь приступим к решению квадратного уравнения. Допустим, тебе нужно найти корни у этого уравнения:

Конечно, ты можешь сейчас начать считать через дискриминант, либо по теореме Виета, но многие на нервах ошибаются при переумножении или в возведении в квадрат, особенно, если пример с большими числами, а калькулятора, как ты знаешь, у тебя на экзамене не будет… Поэтому, давай попробуем немного расслабиться и порисовать, решая данное уравнение.

Графически найти решения данного уравнения можно различными способами. Рассмотрим различные варианты, а уже ты сам выберешь, какой больше всего тебе понравится.

Способ 1. Напрямую

Просто строим параболу по данному уравнению:

Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:

Ты скажешь «Стоп! Формула для очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни. Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!

Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:

Точно такой же ответ? Молодец! И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, .

Ты знаешь, что парабола симметрична относительно своей вершины, например:

Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:

Возвращаемся к нашей параболе. Для нашего случая точка . Нам необходимо еще две точки, соответственно, можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней? Мне удобней работать с положительными, поэтому я рассчитаю при и .

При :

Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:

Как ты думаешь, что является решением уравнения? Правильно, точки, в которых , то есть и . Потому что .

И если мы говорим, что , то значит, что тоже должен быть равен , или .

Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!

Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант. Что у тебя получилось? То же самое? Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!

Способ 2. С разбивкой на несколько функций

Возьмем все тоже наше уравнение: , но запишем его несколько по-другому, а именно:

Можем мы так записать? Можем, так как преобразование равносильно. Смотрим дальше.

Построим отдельно две функции:

— графиком является простая парабола, которую ты с легкостью построишь даже без определения вершины с помощью формул и составления таблицы для определения прочих точек.
— графиком является прямая, которую ты так же легко построишь, прикинув значения и в голове даже не прибегая к калькулятору.

Построил? Сравним с тем, что вышло у меня:

Как ты считаешь, что в данном случае является корнями уравнения? Правильно! Координаты по , которые получились при пересечении двух графиков и , то есть:

Соответственно, решением данного уравнения являются:

Что скажешь? Согласись, этот способ решения намного легче, чем предыдущий и даже легче, чем искать корни через дискриминант! А если так, попробуй данным способом решить следующее уравнение:

Что у тебя получилось? Сравним наши графики:

По графикам видно, что ответами являются:

Справился? Молодец! Теперь посмотрим уравнения чууууть-чуть посложнее, а именно, решение смешанных уравнений, то есть уравнений, содержащих функции разного вида.

Графическое решение смешанных уравнений

Теперь попробуем решить следующее:

Конечно, можно привести все к общему знаменателю, найти корни получившегося уравнения, не забыв при этом учесть ОДЗ, но мы опять же, попробуем решить графически, как делали во всех предыдущих случаях.

В этот раз давай построим 2 следующих графика:

— графиком является гипербола
— графиком является прямая, которую ты легко построишь, прикинув значения и в голове даже не прибегая к калькулятору.

Осознал? Теперь займись построением.

Вот что вышло у меня:

Глядя на этот рисунок, скажи, что является корнями нашего уравнения ?

Правильно, и . Вот и подтверждение:

Попробуй подставить наши корни в уравнение. Получилось?

При : .

Все верно! Согласись, графически решать подобные уравнения одно удовольствие!

Попробуй самостоятельно графическим способом решить уравнение:

Даю подсказку: перенеси часть уравнения в правую сторону, чтобы с обоих сторон оказались простейшие для построения функции. Намек понял? Действуй!

Теперь посмотрим, что у тебя вышло:

, соответственно:

— кубическая парабола.
— обыкновенная прямая.

Ну и строим:

Как ты уже давно у себя записал, корнем данного уравнения является — .

Прорешав такое большое количество примеров, уверена, ты осознал как можно легко и быстро решать уравнения графическим путем. Настало время разобраться, как решать подобным способом системы.

Графическое решение систем

Графическое решение систем по сути ничем не отличается от графического решения уравнений. Мы так же будем строить два графика ,и их точки пересечения и будут являться корнями данной системы. Один график – одно уравнение, второй график – другое уравнение. Все предельно просто!

Начнем с самого простого – решение систем линейных уравнений.

Решение систем линейных уравнений

Допустим, у нас есть следующая система:

Для начала преобразуем ее таким образом, чтобы слева было все, что связано с , а справа – что связано с . Иными словами, запишем данные уравнения как функцию в привычном для нас виде:

А теперь просто строим две прямые. Что в нашем случае является решением? Правильно! Точка их пересечения! И здесь необходимо быть очень-очень внимательным! Подумай, почему? Намекну: мы имеем дело с системой: в системе есть и , и … Намек понял?

Все верно! Решая систему, мы должны смотреть обе координаты, а не только , как при решении уравнений! Еще один важный момент – правильно их записать и не перепутать, где у нас значение , а где значение ! Записал? Теперь давай все сравним по порядку:

И ответы: и . Сделай проверку – подставь найденные корни в систему и убедись, правильно ли мы ее решили графическим способом?

Все сошлось? Идем дальше!

Решение систем нелинейных уравнений

А что если вместо одной прямой, у нас будет квадратное уравнение? Да ничего страшного! Просто ты вместо прямой построишь параболу! Не веришь? Попробуй решить следующую систему:

Какой наш следующий шаг? Правильно, записать так, чтобы нам было удобно строить графики:

А теперь так вообще дело за малым – построил быстренько и вот тебе решение! Строим:

Графики получились такими же? Теперь отметь на рисунке решения системы и грамотно запиши выявленные ответы!

Все сделал? Сравни с моими записями:

При , .

Все верно? Молодец! Ты уже щелкаешь подобные задачи как орешки! А раз так, дадим тебе систему посложнее:

Что мы делаем? Правильно! Записываем систему так, чтобы было удобно строить:

Немного тебе подскажу, так как система выглядит ну очень не простой! Строя графики, строй их «побольше», а главное, не удивляйся количеству точек пересечения.

Итак, поехали! Выдохнул? Теперь начинай строить!

Ну как? Красиво? Сколько точек пересечения у тебя получилось? У меня три! Давай сравнивать наши графики:

Так же? Теперь аккуратно запиши все решения нашей системы:

При , .

А теперь еще раз посмотри на систему:

Представляешь, что ты решил это за каких-то 15 минут? Согласись, математика – это все-таки просто, особенно, когда глядя на выражение, не боишься ошибиться, а берешь и решаешь! Ты большой молодец!

Графическое решение неравенств

Графическое решение линейных неравенств

После последнего примера тебе все по плечу! Сейчас выдохни – по сравнению с предыдущими разделами этот будет очень-очень легким!

Начнем мы, как обычно с графического решения линейного неравенства. Например, вот этого:

Для начала проведем простейшие преобразования – раскроем скобки полных квадратов и приведем подобные слагаемые:

Что мы делаем дальше? Правильно, делим обе части на отрицательное число , при этом не забывая поменять знак неравенства на противоположный (если не помнишь это, посмотри тему «Линейные неравенства»:

Неравенство нестрогое, поэтому — не включается в промежуток, и решением будут являться все точки, которые находятся правее , так как больше , больше и так далее:

Ответ:

Вот и все! Легко? Давай решим простое неравенство с двумя переменными:

Нарисуем в системе координат функцию .

Такой график у тебя получился? А теперь внимательно смотрим, что там у нас в неравенстве? Меньше ? Значит, закрашиваем все, что находится левее нашей прямой. А если было бы больше ? Правильно, тогда закрашивали бы все, что находится правее нашей прямой. Все просто.

Все решения данного неравенства «затушеваны» оранжевым цветом. Вот и все, неравенство с двумя переменными решено. Это значит, что координаты и любой точки из закрашенной области – и есть решения.

Графическое решение квадратных неравенств

Теперь будем разбираться с тем, как графически решать квадратные неравенства.

Но прежде, чем перейти непосредственно к делу, давай повторим некоторый материал, касающийся квадратной функции .

Что показывает нам знак при коэффициенте ? Верно, куда направлены ветви параболы – вверх или вниз (не помнишь? Почитай теорию «Квадратичная функция»).

А за что у нас отвечает дискриминант? Правильно, за положение графика относительно оси (если не помнишь этого, то тогда точно прочти теорию о квадратичных функциях).

В любом случае, вот тебе небольшая табличка-напоминалка:

Теперь, когда мы освежили в памяти весь материал, перейдем к делу – решим графически неравенство .

Сразу тебе скажу, что есть два варианта его решения.

Вариант 1

Записываем нашу параболу как функцию:

По формулам определяем координаты вершины параболы (точно так же, как и при решении квадратных уравнений):

Посчитал? Что у тебя получилось?

Теперь возьмем еще две различных точки и посчитаем для них :

Начинаем строить одну ветвь параболы:

Симметрично отражаем наши точки на другую ветвь параболы:

А теперь возвращаемся к нашему неравенству .

Нам необходимо, чтобы было меньше нуля, соответственно:

Как построить график функции

В этой статье разобран самый простой метод получения графика функции.

Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.

Итак, алгоритм по шагам:

1. Представьте, как выглядит ваш график.

Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.

Пример: Построить график функции $y=-$$\frac{2}{x}$

Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:

2. Составьте таблицу точек, принадлежащих графику:

Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».

Пример: $y=-$$\frac{2}{x}$

при $x=-1$		$y=-$$\frac{2}{-1}$$=2$
при $x=0$		$y$ — не существует (делить на ноль нельзя)
при $x=1$		$y=-$$\frac{2}{1}$$=-2$
при $x=2$		$y=-$$\frac{2}{2}$$=-1$
при $x=3$		$y=-$$\frac{2}{3}$
при $x=4$		$y=-$$\frac{2}{4}$$=-$$\frac{1}{2}$

Результат вычислений удобно представлять в виде таблицы, примерно такой:

$x$	$-1$	$0$	$1$	$2$	$3$	$4$
$y$	$2$	$-$	$-2$	$-1$	$-$$\frac{2}{3}$	$-$$\frac{1}{2}$

Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.

4. Постройте координатную плоскость и отметьте на ней точки из таблицы.

Пример:

5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.

Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с $x=-2$, $x=-4$, $x=$$\frac{1}{2}$ и $x=-$$\frac{1}{2}$

при $x=-2$		$y=-$$\frac{2}{-2}$$=1$
при $x=-4$		$y=-$$\frac{2}{-4}$$=$$\frac{1}{2}$
при $x=$$\frac{1}{2}$		$y=-$$\frac{2}{\frac{1}{2}}$$=-2:$$\frac{1}{2}$$=-2 \cdot 2=-4$
при $x=-$$\frac{1}{2}$		$y=-$$\frac{2}{-\frac{1}{2}}$$=-2:(-$$\frac{1}{2}$$)$$=-2 \cdot (-2)=4$

$x$	$-1$	$0$	$1$	$2$	$3$	$4$	$-2$	$-4$	$\frac{1}{2}$	$-$$\frac{1}{2}$
$y$	$2$	$-$	$-2$	$-1$	$-$$\frac{2}{3}$	$-$$\frac{1}{2}$	$1$	$\frac{1}{2}$	$-4$	$4$

6. Постройте график

Теперь аккуратно и плавно соединяем точки.

Готово!

Скачать статью

Строим график функции, заданный системой уравнений, в EXCEL. Примеры и описание

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

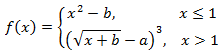
Требуется на отрезке [-1; 4] построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ : О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL . О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL .

Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1 ):

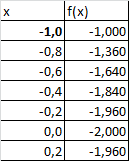
Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

Чтобы построить диаграмму типа Точечная:

выделите любую ячейку таблицы;
во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами .

Чтобы построить диаграмму типа График:

выделите любую столбец f(x) вместе с заголовком;
во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами .

У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных .

Решение (2 ряда данных)

Создадим другую таблицу с исходными данными в файле примера, лист График :

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола. Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы. При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции y=x^2 имеет вид:

y=x^2

Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции y=x^2 , составим таблицу:

y=x^2

Внимание! Если в уравнении квадратичной функции старший коэффициент a=1 , то график квадратичной функции имеет ровно такую же форму, как график функции y=x^2 при любых значениях остальных коэффициентов.

График функции y=-x^2 имеет вид:

y=-x^2

Для нахождения координат базовых точек составим таблицу:

y=-x^2

Обратите внимание, что график функции y=-x^2 симметричен графику функции y=x^2 относительно оси ОХ.

Итак, мы заметили:

Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если D<0 ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если a>0 ,то график функции выглядит как-то так:

2. Если D=0 ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если a>0 ,то график функции выглядит примерно так:

3. Если D>0 ,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:

$x_1={-b+sqrt{D}}/{2a}$ , $x_2={-b-sqrt{D}}/{2a}$

Если a>0 ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

$x_0=-{b/{2a}}$

$y_0=-{D/{4a}}=y(x_0)$

Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: y(0)=c .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны на рисунке:

y(0)=c

Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции

1. Направление ветвей параболы.

Так как a=2>0 ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение:

$x_1={-3+7}/4=1$ , $x_1={-3-7}/4=-2,5$

3. Координаты вершины параболы:

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

$y_0=-{D/{4a}}=-49/8=-6,125$

Этот способ можно несколько упростить.

1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

$x_0=-{b/{2a}}=-3/4 =-0,75$

$y_0=-{D/{4a}}=-49/8=-6,125$

Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:

$y_0=-{D/{4a}}=-49/8=-6,125$

Нанесем эти точки на координатную плоскость и соединим плавной линией:

$y_0=-{D/{4a}}=-49/8=-6,125$

2. Уравнение квадратичной функции имеет вид — в этом уравнении x_0;y_0 — координаты вершины параболы

или в уравнении квадратичной функции a=1 , и второй коэффициент — четное число.

Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

сначала построить график функции ,
затем одинаты всех точек графика умножить на 2,
затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
а затем вдоль оси OY на 4 единицы вверх:

y=x^2

Теперь рассмотрим построение графика функции . В уравнении этой функции a=1 , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат:

Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

3. Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда

2. Координаты вершины параболы: $x_0={x_1+x_2}/2={2-1}/2=1/2$

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на координатную плоскость и построим график:

$y_0=y(-1)=({1/2}-2)({1/2}+1)=-9/4=-2,25$

График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения ,

— сдвига графика функции вдоль оси от значения
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

2 здесь у = х ** 2 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [ ‘левый’]. set_position ( ‘центр’) ax.spines [ ‘снизу’]. set_position ( ‘нулевой’) ax.spines [ ‘право’]. set_color ( ‘ни’) ax.spines [ ‘сверху’]. set_color ( ‘ни’) ax.xaxis.set_ticks_position ( ‘снизу’) ax.yaxis.set_ticks_position ( ‘левый’) # построить график функции plt.plot (x, y, ‘r’) # показать сюжет plt.show ()

кубическое уравнение

Далее мы построим простейшую кубическую функцию $ y = x ^ {3} $.3 здесь у = х ** 3 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [ ‘левый’]. set_position ( ‘центр’) ax.spines [ ‘снизу’]. set_position ( ‘центр’) ax.spines [ ‘право’]. set_color ( ‘ни’) ax.spines [ ‘сверху’]. set_color ( ‘ни’) ax.xaxis.set_ticks_position ( ‘снизу’) ax.yaxis.set_ticks_position ( ‘левый’) # построить график функции plt.plot (x, y, ‘g’) # показать сюжет plt.show ()

Тригонометрические Функции

Здесь мы строим тригонометрическую функцию $ y = \ text {sin} (x) $ для значений $ x $ между $ — \ pi $ и $ \ pi $.Метод linspace () имеет интервал от $ — \ pi $ до $ \ pi $.


импортировать matplotlib.pyplot как plt
импортировать numpy как np

# 100 линейно расположенных чисел
x = np.linspace (-np.pi, np.pi, 100)

# функция, которая здесь y = sin (x)
y = np.sin (x)

# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [ 'левый']. set_position ( 'центр')
ax.spines [ 'снизу'].set_position ( 'центр')
ax.spines [ 'право']. set_color ( 'ни')
ax.spines [ 'сверху']. set_color ( 'ни')
ax.xaxis.set_ticks_position ( 'снизу')
ax.yaxis.set_ticks_position ( 'левый')

# построить график функции
plt.plot (x, y, 'b')

# показать сюжет
plt.show ()

Давайте построим его вместе с еще двумя функциями: $ y = 2 \ text {sin} (x) $ и $ y = 3 \ text {sin} (x) $. На этот раз мы помечаем функции.


импортировать matplotlib.pyplot как plt
импортировать numpy как np

# 100 линейно расположенных чисел
x = np.linspace (-np.pi, np.pi, 100)

# функция, которая здесь y = sin (x)
y = np.sin (x)

# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [ 'левый']. set_position ( 'центр')
ax.spines [ 'снизу']. set_position ( 'центр')
ax.spines [ 'право']. set_color ( 'ни')
Топор.шипы [ 'сверху']. set_color ( 'ни')
ax.xaxis.set_ticks_position ( 'снизу')
ax.yaxis.set_ticks_position ( 'левый')

# построить функции
plt.plot (x, y, 'b', label = 'y = sin (x)')
plt.plot (x, 2 * y, 'c', label = 'y = 2sin (x)')
plt.plot (x, 3 * y, 'r', label = 'y = 3sin (x)')

plt.legend (loc = 'верхний левый')

# показать сюжет
plt.show ()

И здесь мы строим вместе оба $ y = \ text {sin} (x) $ и $ y = \ text {cos} (x) $ на одном и том же интервале $ — \ pi $ до $ \ pi $.


импортировать matplotlib.pyplot как plt
импортировать numpy как np

# 100 линейно расположенных чисел
x = np.linspace (-np.pi, np.pi, 100)

# функции, которые y = sin (x) и z = cos (x) здесь
y = np.sin (x)
z = np.cos (x)

# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines [ 'левый']. set_position ( 'центр')
ax.spines [ 'снизу']. set_position ( 'центр')
ax.spines [ 'право'].set_color ( 'ни')
ax.spines [ 'сверху']. set_color ( 'ни')
ax.xaxis.set_ticks_position ( 'снизу')
ax.yaxis.set_ticks_position ( 'левый')

# построить функции
plt.plot (x, y, 'c', label = 'y = sin (x)')
plt.plot (x, z, 'm', label = 'y = cos (x)')

plt.legend (loc = 'верхний левый')

# показать сюжет
plt.show ()

Экспоненциальная функция

Экспоненциальная функция $ y = e ^ {x} $ никогда не будет иметь отрицательных значений для любого значения $ x $.Икс’) plt.legend (loc = ‘верхний левый’) # показать сюжет plt.show () ,Математическая оптимизация

— Построить и решить уравнение в R

Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру

Как построить кривую функции в R

Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру

Как построить нелинейную систему из 3 уравнений с 3 символическими переменными в MATLAB? Переполнение стека

Товары
Клиенты
Случаи использования

Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру

Published in Разное

при \(x=-1\)		\(y=-\)\(\frac{2}{-1}\)\(=2\)
при \(x=0\)		\(y\) — не существует (делить на ноль нельзя)
при \(x=1\)		\(y=-\)\(\frac{2}{1}\)\(=-2\)
при \(x=2\)		\(y=-\)\(\frac{2}{2}\)\(=-1\)
при \(x=3\)		\(y=-\)\(\frac{2}{3}\)
при \(x=4\)		\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\)

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(y\)	\(2\)	\(-\)	\(-2\)	\(-1\)	\(-\)\(\frac{2}{3}\)	\(-\)\(\frac{1}{2}\)

при \(x=-2\)		\(y=-\)\(\frac{2}{-2}\)\(=1\)
при \(x=-4\)		\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\)
при \(x=\)\(\frac{1}{2}\)		\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\)
при \(x=-\)\(\frac{1}{2}\)		\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\)

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(-2\)	\(-4\)	\(\frac{1}{2}\)	\(-\)\(\frac{1}{2}\)
\(y\)	\(2\)	\(-\)	\(-2\)	\(-1\)	\(-\)\(\frac{2}{3}\)	\(-\)\(\frac{1}{2}\)	\(1\)	\(\frac{1}{2}\)	\(-4\)	\(4\)

Построение графиков функций

Алгебра. Урок 5. Графики функций

Графическое решение уравнений

Графическое решение линейных уравнений

Графическое решение квадратных уравнений

Способ 1. Напрямую

Способ 2. С разбивкой на несколько функций

Графическое решение смешанных уравнений

Графическое решение систем

Решение систем линейных уравнений

Решение систем нелинейных уравнений

Графическое решение неравенств

Графическое решение линейных неравенств

Графическое решение квадратных неравенств

Вариант 1

Как построить график функции

Решение (1 ряд данных)

Решение (2 ряда данных)

Решение (3 ряда данных)

Квадратичная функция и ее график

График квадратичной функции.

кубическое уравнение

Тригонометрические Функции

Экспоненциальная функция

— Построить и решить уравнение в R

Как построить кривую функции в R

Ваш комментарий будет первым

Добавить комментарий Отменить ответ